2.6: Exact Equations
- Last updated
- Save as PDF
- Page ID
- 30699
In this section it is convenient to write first order differential equations in the form
\[\label{eq:2.5.1} M(x,y)\,dx+N(x,y)\,dy=0.\]
This equation can be interpreted as
\[\label{eq:2.5.2} M(x,y)+N(x,y)\,{dy\over dx}=0,\]
where \(x\) is the independent variable and \(y\) is the dependent variable, or as
\[\label{eq:2.5.3} M(x,y)\,{dx\over dy}+N(x,y)=0,\]
where \(y\) is the independent variable and \(x\) is the dependent variable. Since the solutions of Equation \ref{eq:2.5.2} and Equation \ref{eq:2.5.3} will often have to be left in implicit form we will say that \(F(x,y)=c\) is an implicit solution of Equation \ref{eq:2.5.1} if every differentiable function \(y=y(x)\) that satisfies \(F(x,y)=c\) is a solution of Equation \ref{eq:2.5.2} and every differentiable function \(x=x(y)\) that satisfies \(F(x,y)=c\) is a solution of Equation \ref{eq:2.5.3}
Here are some examples:
| Equation \ref{eq:2.5.1} | Equation \ref{eq:2.5.2} | Equation \ref{eq:2.5.3} |
|---|---|---|
| \(3x^2y^2\,dx+2x^3y\,dy =0\) | \(3x^2y^2+2x^3y\, {dy\over dx} =0\) | \(3x^2y^2\, {dx\over dy}+2x^3y=0\) |
| \((x^2+y^2)\,dx +2xy\,dy=0\) | \((x^2+y^2)+2xy\, {dy\over dx}=0\) | \((x^2+y^2)\, {dx\over dy} +2xy=0\) |
| \(3y\sin x\,dx-2xy\cos x\,dy =0\) | \(3y\sin x-2xy\cos x\, {dy\over dx} =0\) | \(3y\sin x\, {dx\over dy}-2xy\cos x =0\) |
Note that a separable equation can be written as Equation \ref{eq:2.5.1} as
\[M(x)\,dx+N(y)\,dy=0. \nonumber\]
we will develop a method for solving Equation \ref{eq:2.5.1} under appropriate assumptions on \(M\) and \(N\). This method is an extension of the method of separation of variables. Before stating it we consider an example.
Example \(\PageIndex{1}\)
Show that
\[\label{eq:2.5.4} x^4y^3+x^2y^5+2xy=c \]
is an implicit solution of
\[\label{eq:2.5.5} (4x^3y^3+2xy^5+2y)\,dx+(3x^4y^2+5x^2y^4+2x)\,dy=0. \]
Solution
Regarding \(y\) as a function of \(x\) and differentiating Equation \ref{eq:2.5.4} implicitly with respect to \(x\) yields
\[(4x^3y^3+2xy^5+2y)+(3x^4y^2+5x^2y^4+2x)\,{dy\over dx}=0. \nonumber\]
Similarly, regarding \(x\) as a function of \(y\) and differentiating Equation \ref{eq:2.5.4} implicitly with respect to \(y\) yields
\[(4x^3y^3+2xy^5+2y){dx\over dy}+(3x^4y^2+5x^2y^4+2x)=0. \nonumber\]
Therefore Equation \ref{eq:2.5.4} is an implicit solution of Equation \ref{eq:2.5.5} in either of its two possible interpretations.
You may think Example \(\PageIndex{1}\) is pointless, since concocting a differential equation that has a given implicit solution is not particularly interesting. However, it illustrates the next important theorem, which we will prove by using implicit differentiation, as in Example \(\PageIndex{1}\).
Theorem \(\PageIndex{1}\)
If \(F=F(x,y)\) has continuous partial derivatives \(F_x\) and \(F_y\), then
\[\label{eq:2.5.6} F(x,y)=c \]
(with \(c\) as a constant) is an implicit solution of the differential equation
\[\label{eq:2.5.7} F_x(x,y)\,dx+F_y(x,y)\,dy=0.\]
- Proof
-
Regarding \(y\) as a function of \(x\) and differentiating Equation \ref{eq:2.5.6} implicitly with respect to \(x\) yields
\[F_x(x,y)+F_y(x,y)\,{dy\over dx}=0. \nonumber\]
On the other hand, regarding \(x\) as a function of \(y\) and differentiating Equation \ref{eq:2.5.6} implicitly with respect to \(y\) yields
\[F_x(x,y)\,{dx\over dy}+F_y(x,y)=0. \nonumber\]
Thus, Equation \ref{eq:2.5.6} is an implicit solution of Equation \ref{eq:2.5.7} in either of its two possible interpretations.
We will say that the equation
\[\label{eq:2.5.8} M(x,y)\,dx+N(x,y)\,dy=0\]
is exact on an an open rectangle \(R\) if there’s a function \(F=F(x,y)\) such \(F_x\) and \(F_y\) are continuous, and
\[\label{eq:2.5.9} F_x(x,y)=M(x,y) \quad \text{and} \quad F_y(x,y)=N(x,y)\]
for all \((x,y)\) in \(R\). This usage of “exact” is related to its usage in calculus, where the expression
\[F_x(x,y)\,dx+F_y(x,y)\,dy\nonumber \]
(obtained by substituting Equation \ref{eq:2.5.9} into the left side of Equation \ref{eq:2.5.8}) is the exact differential of \(F\).
Example \(\PageIndex{1}\) shows that it is easy to solve Equation \ref{eq:2.5.8} if it is exact and we know a function \(F\) that satisfies Equation \ref{eq:2.5.9}. The important questions are:
- Question 1. Given an equation Equation \ref{eq:2.5.8}, how can we determine whether it is exact?
- Question 2. If Equation \ref{eq:2.5.8} is exact, how do we find a function \(F\) satisfying Equation \ref{eq:2.5.9}?
To discover the answer to Question 1, assume that there’s a function \(F\) that satisfies Equation \ref{eq:2.5.9} on some open rectangle \(R\), and in addition that \(F\) has continuous mixed partial derivatives \(F_{xy}\) and \(F_{yx}\). Then a theorem from calculus implies that \[\label{eq:2.5.10} F_{xy}=F_{yx}.\] If \(F_x=M\) and \(F_y=N\), differentiating the first of these equations with respect to \(y\) and the second with respect to \(x\) yields
\[\label{eq:2.5.11} F_{xy}=M_y \quad \text{and} \quad F_{yx}=N_x.\]
From Equation \ref{eq:2.5.10} and Equation \ref{eq:2.5.11}, we conclude that a necessary condition for exactness is that \(M_y=N_x\). This motivates the next theorem, which we state without proof.
Theorem \(\PageIndex{2}\): The Exactness Condition
Suppose \(M\) and \(N\) are continuous and have continuous partial derivatives \(M_y\) and \(N_x\) on an open rectangle \(R.\) Then
\[M(x,y)\,dx+N(x,y)\,dy=0\nonumber \]
is exact on \(R\) if and only if
\[\label{eq:2.5.12} M_y(x,y)=N_x(x,y)\]
for all \((x,y)\) in \(R.\).
To help you remember the exactness condition, observe that the coefficients of \(dx\) and \(dy\) are differentiated in Equation \ref{eq:2.5.12} with respect to the “opposite” variables; that is, the coefficient of \(dx\) is differentiated with respect to \(y\), while the coefficient of \(dy\) is differentiated with respect to \(x\).
Example \(\PageIndex{2}\)
Show that the equation
\[3x^2y\,dx+4x^3\,dy=0\nonumber \]
is not exact on any open rectangle.
Solution
Here
\[M(x,y)=3x^2y \quad \text{and} \quad N(x,y)=4x^3 \nonumber\]
so
\[M_y(x,y)=3x^2 \quad \text{and} N_x(x,y)=12 x^2. \nonumber\]
Therefore \(M_y=N_x\) on the line \(x=0\), but not on any open rectangle, so there’s no function \(F\) such that \(F_x(x,y)=M(x,y)\) and \(F_y(x,y)=N(x,y)\) for all \((x,y)\) on any open rectangle.
The next example illustrates two possible methods for finding a function \(F\) that satisfies the condition \(F_x=M\) and \(F_y=N\) if \(M\,dx+N\,dy=0\) is exact.
Example \(\PageIndex{3}\)
Solve
\[\label{eq:2.5.13} (4x^3y^3+3x^2)\,dx+(3x^4y^2+6y^2)\,dy=0.\]
Solution (Method 1)
Here \[M(x,y)=4x^3y^3+3x^2,\quad N(x,y)=3x^4y^2+6y^2,\nonumber \] and \[M_y(x,y)=N_x(x,y)=12 x^3y^2\nonumber \] for all \((x,y)\). Therefore Theorem \(\PageIndex{2}\) implies that there’s a function \(F\) such that
\[\label{eq:2.5.14} F_x(x,y)=M(x,y)=4x^3y^3+3x^2\]
and
\[\label{eq:2.5.15} F_y(x,y)=N(x,y)=3x^4y^2+6y^2\]
for all \((x,y)\). To find \(F\), we integrate Equation \ref{eq:2.5.14} with respect to \(x\) to obtain
\[\label{eq:2.5.16} F(x,y)=x^4y^3+x^3+\phi(y),\]
where \(\phi (y)\) is the “constant” of integration. (Here \(\phi\) is “constant” in that it is independent of \(x\), the variable of integration.) If \(\phi\) is any differentiable function of \(y\) then \(F\) satisfies Equation \ref{eq:2.5.14}. To determine \(\phi\) so that \(F\) also satisfies Equation \ref{eq:2.5.15}, assume that \(\phi\) is differentiable and differentiate \(F\) with respect to \(y\). This yields
\[F_y(x,y)=3x^4y^2+\phi'(y). \nonumber\]
Comparing this with Equation \ref{eq:2.5.15} shows that
\[\phi'(y)=6y^2. \nonumber\]
We integrate this with respect to \(y\) and take the constant of integration to be zero because we are interested only in finding some \(F\) that satisfies Equation \ref{eq:2.5.14} and Equation \ref{eq:2.5.15}. This yields
\[\phi (y)=2y^3. \nonumber\]
Substituting this into Equation \ref{eq:2.5.16} yields
\[\label{eq:2.5.17} F(x,y)=x^4y^3+x^3+2y^3.\]
Now Theorem \(\PageIndex{1}\) implies that \[x^4y^3+x^3+2y^3=c\nonumber \] is an implicit solution of Equation \ref{eq:2.5.13}. Solving this for \(y\) yields the explicit solution
\[y=\left(c-x^3\over2+x^4\right)^{1/3}. \nonumber\]
Solution (Method 2)
Instead of first integrating Equation \ref{eq:2.5.14} with respect to \(x\), we could begin by integrating Equation \ref{eq:2.5.15} with respect to \(y\) to obtain
\[\label{eq:2.5.18} F(x,y)=x^4y^3+2y^3+\psi (x),\]
where \(\psi\) is an arbitrary function of \(x\). To determine \(\psi\), we assume that \(\psi\) is differentiable and differentiate \(F\) with respect to \(x\), which yields
\[F_x(x,y)=4x^3y^3+\psi'(x). \nonumber\]
Comparing this with Equation \ref{eq:2.5.14} shows that
\[\psi'(x)=3x^2. \nonumber\]
Integrating this and again taking the constant of integration to be zero yields
\[\psi(x)=x^3. \nonumber\]
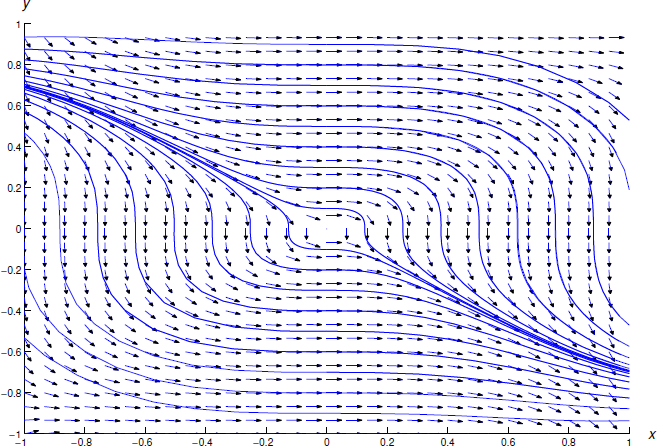
Substituting this into Equation \ref{eq:2.5.18} yields Equation \ref{eq:2.5.17}.
Figure \(\PageIndex{1}\) shows a direction field and some integral curves of Equation \ref{eq:2.5.13}.
Here’s a summary of the procedure used in Method 1 of this example. You should summarize procedure used in Method 2.
HOWTO: Procedure For Solving An Exact Equation (Method 1)
- Step 1. Check that the equation \[\label{eq:2.5.19} M(x,y)\,dx+N(x,y)\,dy=0\] satisfies the exactness condition \(M_y=N_x\). If not, don’t go further with this procedure.
- Step 2. Integrate \[{\partial F(x,y)\over\partial x}=M(x,y)\nonumber \] with respect to \(x\) to obtain \[\label{eq:2.5.20} F(x,y)=G(x,y)+\phi(y),\] where \(G\) is an antiderivative of \(M\) with respect to \(x\), and \(\phi\) is an unknown function of \(y\).
- Step 3. Differentiate Equation \ref{eq:2.5.20} with respect to \(y\) to obtain \[{\partial F(x,y)\over\partial y}={\partial G(x,y)\over\partial y}+\phi'(y). \nonumber\]
- Step 4. Equate the right side of this equation to \(N\) and solve for \(\phi'\); thus, \[{\partial G(x,y)\over\partial y}+\phi'(y)=N(x,y), \quad \text{so} \quad \phi'(y)=N(x,y)-{\partial G(x,y)\over\partial y}. \nonumber\]
- Step 5. Integrate \(\phi'\) with respect to \(y\), taking the constant of integration to be zero, and substitute the result in Equation \ref{eq:2.5.20} to obtain \(F(x,y)\).
- Step 6. Set \(F(x,y)=c\) to obtain an implicit solution of Equation \ref{eq:2.5.19}. If possible, solve for \(y\) explicitly as a function of \(x\).
It’s a common mistake to omit Step 6 in the procedure above. However, it is important to include this step, since F isn’t itself a solution of Equation \ref{eq:2.5.19}. Many equations can be conveniently solved by either of the two methods used in Example \(\PageIndex{3}\). However, sometimes the integration required in one approach is more difficult than in the other. In such cases we choose the approach that requires the easier integration.
Example \(\PageIndex{4}\)
Solve the equation
\[\label{eq:2.5.21} \left( y e ^ { x y } \tan x + e ^ { x y } \sec ^ { 2 } x \right) d x + x e ^ { x y } \tan x \, dy = 0\]
Solution
We leave it to you to check that \(M_y = N_x\) on any open rectangle where \(\tan x\) and \(\sec x\) are defined. Here we must find a function F such that
\[\label{eq:2.5.22} F_x(x, y) = ye^{xy} \tan x + e^{xy} \sec^2 x\]
and
\[\label{eq:2.5.23} F_y(x, y) = xe^{xy} \tan x. \]
It’s difficult to integrate Equation \ref{eq:2.5.22} with respect to \(x\), but easy to integrate Equation \ref{eq:2.5.23} with respect to \(y\). This yields
\[\label{eq:2.5.24} F(x, y) = e^{xy} \tan x + \psi(x). \]
Differentiating this with respect to \(x\) yields
\[F_x(x, y) = y e^{xy} \tan x + e^{xy} \sec^2 x + \psi'(x). \nonumber\]
Comparing this with Equation \ref{eq:2.5.22} shows that \(\psi'(x) = 0\). Hence, \(\psi\) is a constant, which we can take to be zero in Equation \ref{eq:2.5.24}, and
\[e^{xy} \tan x = c, \nonumber\]
is an implicit solution of Equation \ref{eq:2.5.21}.
Attempting to apply our procedure to an differential equation that is not exact will lead to failure in Step 4, since the function
\[N - \frac { \partial G } { \partial y } \nonumber\]
will not be independent of \(x\) if \(M_y \neq N_x\), and therefore cannot be the derivative of a function of \(y\) alone. Example \(\PageIndex{5}\) illustrates this.
Example \(\PageIndex{5}\)
Verify that the equation
\[\label{eq:2.5.25} 3x^2y^2\,dx+6x^3y\,dy=0\]
is not exact, and show that the procedure for solving exact equations fails when applied to Equation \ref{eq:2.5.25}.
Solution
Here \[M_y(x,y)=6x^2y \quad \text{and} \quad N_x(x,y)=18x^2y,\nonumber \]
so Equation \ref{eq:2.5.25} is not exact. Nevertheless, let us try to find a function \(F\) such that
\[\label{eq:2.5.26} F_x(x,y)=3x^2y^2\]
and
\[\label{eq:2.5.27} F_y(x,y)=6x^3y.\]
Integrating Equation \ref{eq:2.5.26} with respect to \(x\) yields
\[F(x,y)=x^3y^2+\phi(y), \nonumber\]
and differentiating this with respect to \(y\) yields
\[F_y(x,y)=2x^3y+\phi'(y). \nonumber\]
For this equation to be consistent with Equation \ref{eq:2.5.27},
\[6x^3y=2x^3y+\phi'(y), \nonumber\]
or
\[\phi'(y)=4x^3y. \nonumber\]
This is a contradiction, since \(\phi'\) must be independent of \(x\). Therefore the procedure fails.


