6.2: Spring Problems II
- Last updated
- Save as PDF
- Page ID
- 30739
Free Vibrations with Damping
In this section we consider the motion of an object in a spring–mass system with damping. We start with unforced motion, so the equation of motion is
\[\label{eq:6.2.1} my''+cy'+ky=0.\]
Now suppose the object is displaced from equilibrium and given an initial velocity. Intuition suggests that if the damping force is sufficiently weak the resulting motion will be oscillatory, as in the undamped case considered in the previous section, while if it is sufficiently strong the object may just move slowly toward the equilibrium position without ever reaching it. We’ll now confirm these intuitive ideas mathematically. The characteristic equation of Equation \ref{eq:6.2.1} is
\[mr^2+cr+k=0. \nonumber \]
The roots of this equation are
\[\label{eq:6.2.2} r_1={-c-\sqrt{c^2-4mk}\over2m}\quad \text{and} \quad r_2= {-c+\sqrt{c^2-4mk}\over2m}.\]
We saw in Section 5.2 that the form of the solution of Equation \ref{eq:6.2.1} depends upon whether \(c^2-4mk\) is positive, negative, or zero. We’ll now consider these three cases.
Underdamped Motion
We say the motion is underdamped if \(c<\sqrt{4mk}\). In this case \(r_1\) and \(r_2\) in Equation \ref{eq:6.2.2} are complex conjugates, which we write as
\[r_1=-{c\over2m}-\omega_1\,i\quad \text{and} \quad r_2=-{c\over2m}+\omega_1\,i, \nonumber \]
where
\[\omega_1={\sqrt{4mk-c^2}\over2m}. \nonumber \]
The general solution of Equation \ref{eq:6.2.1} in this case is
\[y=e^{-ct/2m}(c_1\cos\omega_1 t+c_2\sin\omega_1 t). \nonumber \]
By the method used in Section 6.1 to derive the amplitude–phase form of the displacement of an object in simple harmonic motion, we can rewrite this equation as
\[\label{eq:6.2.3} y=Re^{-ct/2m}\cos(\omega_1 t-\phi),\]
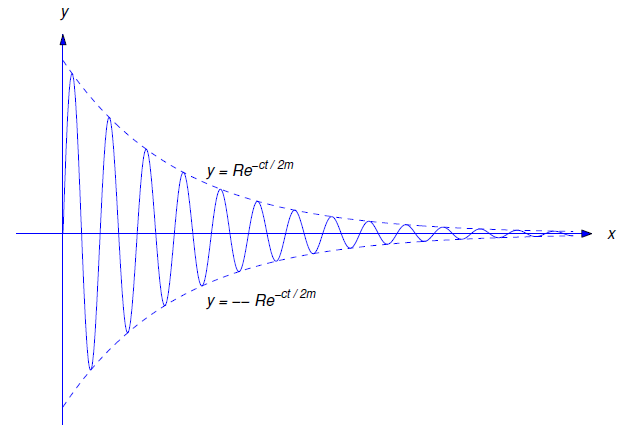
where
\[R=\sqrt{c_1^2+c_2^2},\quad R\cos\phi=c_1,\quad \text{and} \quad R\sin\phi=c_2. \nonumber \]
The factor \(Re^{-ct/2m}\) in Equation \ref{eq:6.2.3} is called the time–varying amplitude of the motion, the quantity \(\omega_1\) is called the frequency, and \(T=2\pi/\omega_1\) (which is the period of the cosine function in Equation \ref{eq:6.2.3} is called the quasi–period. A typical graph of Equation \ref{eq:6.2.3} is shown in Figure 6.2.1 . As illustrated in that figure, the graph of \(y\) oscillates between the dashed exponential curves \(y=\pm Re^{-ct/2m}\).
Overdamped Motion
We say the motion is overdamped if \(c>\sqrt{4mk}\). In this case the zeros \(r_1\) and \(r_2\) of the characteristic polynomial are real, with \(r_1 <r_{2}<0\) (see \ref{eq:6.2.2}), and the general solution of \ref{eq:6.2.1} is
\[y=c_1e^{r_1t}+c_2e^{r_2t}. \nonumber \]
Again \(\lim_{t\to\infty}y(t)=0\) as in the underdamped case, but the motion isn’t oscillatory, since \(y\) can’t equal zero for more than one value of \(t\) unless \(c_1=c_2=0\). (Exercise 6.2.23.)
Critically Damped Motion
We say the motion is critically damped if \(c=\sqrt{4mk}\). In this case \(r_1=r_2=-c/2m\) and the general solution of Equation \ref{eq:6.2.1} is
\[y=e^{-ct/2m}(c_1+c_2t). \nonumber \]
Again \(\lim_{t\to\infty}y(t)=0\) and the motion is nonoscillatory, since \(y\) can’t equal zero for more than one value of \(t\) unless \(c_1=c_2=0\). (Exercise 6.2.22).
Example 6.2.1
Suppose a \(64\) lb weight stretches a spring \(6\) inches in equilibrium and a dashpot provides a damping force of \(c\) lb for each ft/sec of velocity.
- Write the equation of motion of the object and determine the value of \(c\) for which the motion is critically damped.
- Find the displacement \(y\) for \(t>0\) if the motion is critically damped and the initial conditions are \(y(0)=1\) and \(y'(0)=20\).
- Find the displacement \(y\) for \(t>0\) if the motion is critically damped and the initial conditions are \(y(0)=1\) and \(y'(0)=-20\).
Solution a
Here \(m=2\) slugs and \(k=64/.5=128\) lb/ft. Therefore the equation of motion Equation \ref{eq:6.2.1} is
\[\label{eq:6.2.4} 2y''+cy'+128y=0.\]
The characteristic equation is
\[2r^2+cr+128=0, \nonumber \]
which has roots
\[r={-c\pm\sqrt{c^2-8\cdot128}\over4}. \nonumber \]
Therefore the damping is critical if
\[c=\sqrt{8\cdot128}=32\mbox{ lb-sec/ft}. \nonumber \]
Solution b
Setting \(c=32\) in Equation \ref{eq:6.2.4} and cancelling the common factor \(2\) yields
\[y''+16y+64y=0. \nonumber\]
The characteristic equation is
\[r^2+16r+64y=(r+8)^2=0. \nonumber\]
Hence, the general solution is
\[\label{eq:6.2.5} y=e^{-8t}(c_1+c_2t).\]
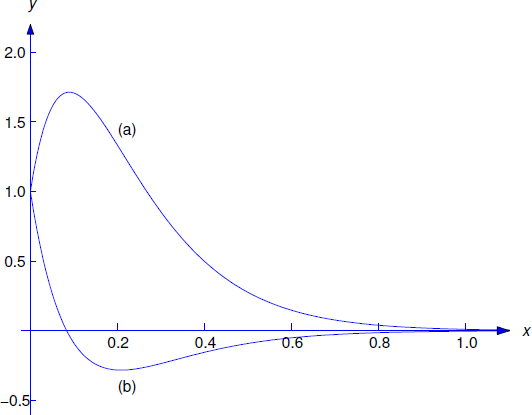
Differentiating this yields
\[\label{eq:6.2.6} y'=-8y+c_2e^{-8t}.\]
6.2.2 Imposing the initial conditions \(y(0)=1\) and \(y'(0)=20\) in the last two equations shows that \(1=c_1\) and \(20=-8+c_2\). Hence, the solution of the initial value problem is
\[y=e^{-8t}(1+28t). \nonumber \]
Therefore the object approaches equilibrium from above as \(t\to\infty\). There’s no oscillation.
Solution c
Imposing the initial conditions \(y(0)=1\) and \(y'(0)=-20\) in Equation \ref{eq:6.2.5} and Equation \ref{eq:6.2.6} yields \(1=c_1\) and \(-20=-8+c_2\). Hence, the solution of this initial value problem is
\[y=e^{-8t}(1-12t). \nonumber \]
Therefore the object moves downward through equilibrium just once, and then approaches equilibrium from below as \(t\to\infty\). Again, there’s no oscillation. The solutions of these two initial value problems are graphed in Figure 6.2.2 .
Example 6.2.2
Find the displacement of the object in Example 6.2.1 if the damping constant is \(c=4\) lb–sec/ft and the initial conditions are \(y(0)=1.5\) ft and \(y'(0)=-3\) ft/sec.
Solution
With \(c=4\), the equation of motion Equation \ref{eq:6.2.4} becomes
\[\label{eq:6.2.7} y''+2y'+64y=0\]
after cancelling the common factor 2. The characteristic equation
\[r^2+2r+64=0 \nonumber\]
has complex conjugate roots\[r={-2\pm\sqrt{4-4\cdot64}\over2}=-1\pm3\sqrt7i. \nonumber\]
Therefore the motion is underdamped and the general solution of Equation \ref{eq:6.2.7} is\[y=e^{-t}(c_1\cos3\sqrt7t+c_2\sin3\sqrt7t). \nonumber\]
Differentiating this yields\[y'=-y+3\sqrt7e^{-t}(-c_1\sin3\sqrt7t+c_2\cos3\sqrt7t). \nonumber\]
Imposing the initial conditions \(y(0)=1.5\) and \(y'(0)=-3\) in the last two equations yields \(1.5=c_1\) and \(-3=-1.5+3\sqrt7c_2\). Hence, the solution of the initial value problem is
\[\label{eq:6.2.8} y=e^{-t}\left({3\over2}\cos3\sqrt7t-{1\over2\sqrt7} \sin3\sqrt7t\right).\]
The amplitude of the function in parentheses is
\[R=\sqrt{\left(\frac{3}{2} \right)^{2}+\left(\frac{1}{2\sqrt{7}} \right)^{2}}=\sqrt{\frac{9}{4}+\frac{1}{4\cdot 7}}=\sqrt{\frac{64}{4\cdot 7}}=\frac{4}{\sqrt{7}} \nonumber\]
Therefore we can rewrite Equation \ref{eq:6.2.8} as\[y={4\over\sqrt7}e^{-t}\cos(3\sqrt7t-\phi), \nonumber\]
where\[\cos\phi={3\over2R}={3\sqrt7\over8}\quad \text{and} \quad\sin\phi=-{1\over2\sqrt7R}= -{1\over8}. \nonumber\]
Therefore \(\phi \cong -0.125\) radians.
Example 6.2.3
Let the damping constant in Example 6.2.1 be \(c=40\) lb–sec/ft. Find the displacement \(y\) for \(t>0\) if \(y(0)=1\) and \(y'(0)=1\).
Solution
With \(c=40\), the equation of motion Equation \ref{eq:6.2.4} reduces to
\[\label{eq:6.2.9} y''+20y'+64y=0\]
after cancelling the common factor 2. The characteristic equation
\[r^2+20r+64=(r+16)(r+4)=0 \nonumber\]
has the roots \(r_1=-4\) and \(r_2=-16\). Therefore the general solution of Equation \ref{eq:6.2.9} is
\[\label{eq:6.2.10} y=c_1e^{-4t}+c_2e^{-16t}.\]
Differentiating this yields
\[y'=-4e^{-4t}-16c_2e^{-16t}. \nonumber\]
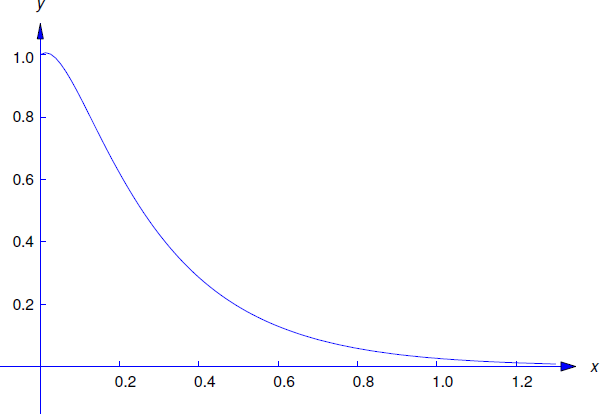
The last two equations and the initial conditions \(y(0)=1\) and \(y'(0)=1\) imply that
\[\begin{array}{rlrl} c_1&+&c_2&=1\\ -4c_1&-&16c_2&=1. \end{array} \nonumber\]
The solution of this system is \(c_1=17/12\), \(c_2=-5/12\). Substituting these into Equation \ref{eq:6.2.10} yields
\[y={17\over12}e^{-4t}-{5\over12}e^{-16t} \nonumber\]
as the solution of the given initial value problem (Figure 6.2.3 ).
Forced Vibrations with Damping
Now we consider the motion of an object in a spring-mass system with damping, under the influence of a periodic forcing function \(F(t)=F_0\cos\omega t\), so that the equation of motion is
\[\label{eq:6.2.11} my''+cy'+ky=F_0\cos\omega t.\]
In Section 6.1 we considered this equation with \(c=0\) and found that the resulting displacement \(y\) assumed arbitrarily large values in the case of resonance (that is, when \(\omega=\omega_0=\sqrt{k/m}\)). Here we’ll see that in the presence of damping the displacement remains bounded for all \(t\), and the initial conditions have little effect on the motion as \(t\to\infty\). In fact, we’ll see that for large \(t\) the displacement is closely approximated by a function of the form
\[\label{eq:6.2.12} y=R\cos(\omega t-\phi),\]
where the amplitude \(R\) depends upon \(m\), \(c\), \(k\), \(F_0\), and \(\omega\). We’re interested in the following question:
QUESTION
Assuming that \(m\), \(c\), \(k\), and \(F_0\) are held constant, what value of \(\omega\) produces the largest amplitude \(R\) in Equation \ref{eq:6.2.12}, and what is this largest amplitude?
To answer this question, we must solve Equation \ref{eq:6.2.11} and determine \(R\) in terms of \(F_0,\omega_0,\omega\), and \(c\). We can obtain a particular solution of Equation \ref{eq:6.2.11} by the method of undetermined coefficients. Since \(\cos\omega t\) does not satisfy the complementary equation
\[my''+cy'+ky=0, \nonumber \]
we can obtain a particular solution of Equation \ref{eq:6.2.11} in the form
\[\label{eq:6.2.13} y_p=A\cos\omega t+B\sin\omega t.\]
Differentiating this yields
\[y_p'=\quad\omega (-A\sin\omega t+B\cos\omega t) \nonumber \]
and
\[y_p''=-\omega^2(A\cos\omega t+B\sin\omega t). \nonumber \]
From the last three equations,
\[my''_p+cy'_p+ky_p=(-m\omega^2A+c\omega B+kA)\cos\omega t+ (-m\omega^2 B-c\omega A+kB)\sin\omega t, \nonumber \]
so \(y_p\) satisfies Equation \ref{eq:6.2.11} if
\[\begin{array}{lll} (k-m\omega^2) A+\quad c\omega B &=F_0\\ -c\omega A\quad+(k-m\omega^2)B&= 0. \end{array} \nonumber \]
Solving for \(A\) and \(B\) and substituting the results into Equation \ref{eq:6.2.13} yields
\[y_p={F_0\over(k-m\omega^2)^2+c^2\omega^2} \left[(k-m\omega^2)\cos\omega t+c\omega\sin\omega t\right], \nonumber \]
which can be written in amplitude–phase form as
\[\label{eq:6.2.14} %\springsteady y_p={F_0\over\sqrt{(k-m\omega^2)^2+c^2\omega^2}} \cos(\omega t-\phi),\]
where
\[\label{eq:6.2.15} \cos\phi={k-m\omega^2\over\sqrt {(k-m\omega^2)^2+c^2\omega^2}}\quad \text{and} \quad \sin\phi={c\omega\over\sqrt{(k-m\omega^2)^2+c^2\omega^2}}.\]
To compare this with the undamped forced vibration that we considered in Section 6.1 it is useful to write
\[\label{eq:6.2.16} k-m\omega^2=m\left({k\over m}-\omega^2\right)= m(\omega_0^2-\omega^2),\]
where \(\omega_0=\sqrt{k/m}\) is the natural angular frequency of the undamped simple harmonic motion of an object with mass \(m\) on a spring with constant \(k\). Substituting Equation \ref{eq:6.2.16} into Equation \ref{eq:6.2.14} yields
\[\label{eq:6.2.17} y_p={F_0\over\sqrt{m^2(\omega^2_0-\omega^2)^2+ c^2\omega^2}}\cos(\omega t-\phi).\]
The solution of an initial value problem
\[my''+cy'+ky=F_0\cos\omega t, \quad y(0)=y_0,\quad y'(0)=v_0, \nonumber \]
is of the form \(y=y_c+y_p\), where \(y_c\) has one of the three forms
\[\begin{aligned} y_c&= e^{-ct/2m}(c_1\cos\omega_1t+c_2\sin\omega_1t),\\ y_c&= e^{-ct/2m}(c_1+c_2t),\\ y_c&= c_1e^{r_1t}+c_2e^{r_2t}\,(r_1,r_2<0).\end{aligned} \nonumber \]
In all three cases \(\displaystyle \lim_{t\to\infty} y_c(t)=0\) for any choice of \(c_1\) and \(c_2\). For this reason we say that \(y_c\) is the transient component of the solution \(y\). The behavior of \(y\) for large \(t\) is determined by \(y_p\), which we call the steady state component of \(y\). Thus, for large \(t\) the motion is like simple harmonic motion at the frequency of the external force.
The amplitude of \(y_p\) in Equation \ref{eq:6.2.17} is
\[\label{eq:6.2.18} R={F_0\over\sqrt{m^2(\omega^2_0-\omega^2)^2+c^2\omega^2}},\]
which is finite for all \(\omega\); that is, the presence of damping precludes the phenomenon of resonance that we encountered in studying undamped vibrations under a periodic forcing function. We’ll now find the value \(\omega_{\max}\) of \(\omega\) for which \(R\) is maximized. This is the value of \(\omega\) for which the function
\[\rho (\omega)=m^2(\omega^2_0-\omega^2)^2+c^2\omega^2 \nonumber \]
in the denominator of Equation \ref{eq:6.2.18} attains its minimum value. By rewriting this as
\[\label{eq:6.2.19} \rho (\omega)=m^2(\omega^4_0+\omega^4)+ (c^2-2m^2\omega^2_0)\omega^2,\]
you can see that \(\rho\) is a strictly increasing function of \(\omega^2\) if
\[c\ge\sqrt{2m^2\omega^2_0}=\sqrt{2mk}. \nonumber \]
(Recall that \(\omega^2_0=k/m\)). Therefore \(\omega_{\max}=0\) if this inequality holds. From Equation \ref{eq:6.2.15}, you can see that \(\phi=0\) if \(\omega=0\). In this case, Equation \ref{eq:6.2.14} reduces to
\[y_p={F_0\over\sqrt{m^2\omega^4_0}}={F_0\over k}, \nonumber \]
which is consistent with Hooke’s law: if the mass is subjected to a constant force \(F_0\), its displacement should approach a constant \(y_p\) such that \(ky_p=F_0\). Now suppose \(c<\sqrt{2mk}\). Then, from Equation \ref{eq:6.2.19},
\[\rho'(\omega)=2\omega(2m^2\omega^2+c^2-2m^2\omega^2_0), \nonumber \]
and \(\omega_{\max}\) is the value of \(\omega\) for which the expression in parentheses equals zero; that is,
\[\omega_{\max}=\sqrt{\omega^2_0-{c^2\over2m^2}} =\sqrt{{k\over m}\left(1-{c^2\over2km}\right)}. \nonumber \]
(To see that \(\rho(\omega_{\max})\) is the minimum value of \(\rho(\omega)\), note that \(\rho'(\omega)<0\) if \(\omega <\omega_{\max}\) and \(\rho'(\omega)>0\) if \(\omega>\omega_{\max}\).) Substituting \(\omega=\omega_{\max}\) in Equation \ref{eq:6.2.18} and simplifying shows that the maximum amplitude \(R_{\max}\) is
\[R_{\max}={2mF_0\over c\sqrt{4mk-c^2}} \quad \text{if} \quad c< \sqrt{2mk}. \nonumber \]
We summarize our results as follows.
Theorem 6.2.1
Suppose we consider the amplitude \(R\) of the steady state component of the solution of
\[my''+cy'+ky=F_0\cos\omega t \nonumber\]
as a function of \(\omega\).
- If \(c\ge\sqrt{2mk}\), the maximum amplitude is \(R_{\max}=F_0/k\) and it is attained when \(\omega= \omega_{\max}=0\).
- If \(c<\sqrt{2mk}\), the maximum amplitude is
\[\label{eq:6.2.20} R_{\max}={2m F_0\over c\sqrt{4mk-c^2}},\]
and it is attained when\[\label{eq:6.2.21} \omega=\omega_{\max}=\sqrt{{k\over m}\left(1-{c^2\over 2km}\right)}.\]
Note that \(R_{\max}\) and \(\omega_{\max}\) are continuous functions of \(c\), for \(c\ge0\), since Equation \ref{eq:6.2.20} and Equation \ref{eq:6.2.21} reduce to \(R_{\max}=F_0/k\) and \(\omega_{\max}=0\) if \(c=\sqrt{2km}\).


