3.4: Finite Difference Calculus
- Page ID
- 13607
This page is a draft and is under active development.
In this section, we will explore further to the method that we explained at the introduction of Quadratic sequences.
Example \(\PageIndex{1}\)
Create a sequence of numbers by finding a relationship between the number of points on the circumference of a circle and the number of regions created by joining the points.
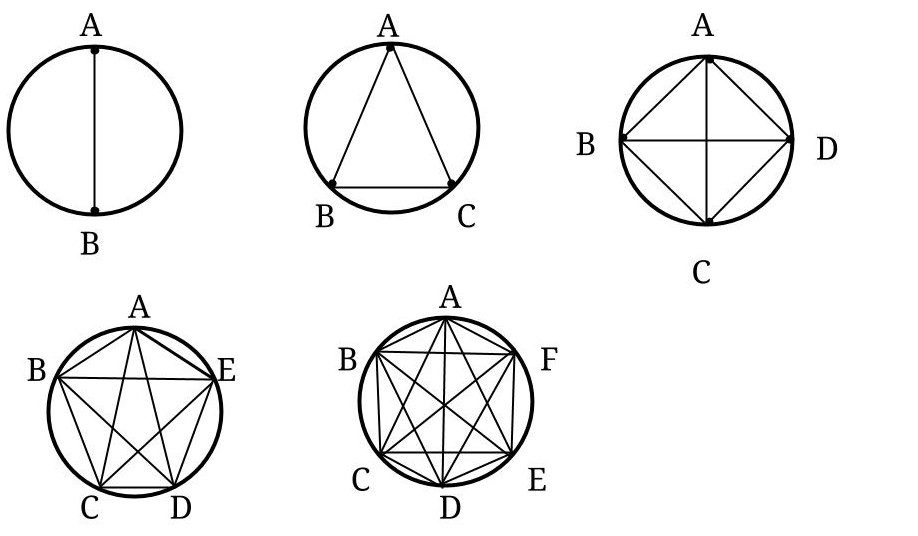
| Number of points on the circle | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Number of regions | 1 | 1 | 2 | 4 | 8 | 16 | 31 | 57 | 99 |
Difference operator
Notation:
Let \(a_n, n=0,1,2,\cdots\) be a sequence of numbers. Then the first difference is defined by \( \Delta a_n = a_{n+1}-a_n, n=0,1,2,\cdots\).
The second difference is defined by \(\Delta (\Delta a_n)= \Delta^2 a_n =\Delta a_{n+1}- \Delta a_n, n=0,1,2,\cdots\).
Further, \(k^{th}\) difference is denoted by \(\Delta^k a_n, n=k,\cdots\). We shall denote that \(\Delta^0 a_n=a_n\).
Example \(\PageIndex{2}\)
Let \(a_n=n^2\), for all \(n \in \mathbb{N}\). Show that \(\Delta^2 a_n=2\).
Solution
\(\Delta a_n =(n+1)^2-n^2= 2n+1,\)
\(\Delta^2 a_n=(2(n+1)+1)-(2n+1)= 2.\)
Rule
Let \(k \in \mathbb{Z_+}\). Let \(a_n=n^k\), for all \(n \in \mathbb{N}\). Then \(\Delta^k a_n=k! \).
Example \(\PageIndex{3}\)
Let \(a_n=c^n\), for all \(n \in \mathbb{N}\). Show that \(\Delta a_n=(c-1) a_n\).
Solution
\(\Delta a_n= c^{n+1}-c^{n}= c^n(c-1) = (c-1) a_n\).
Below are some properties of the difference operator.
Theorem \(\PageIndex{1}\): Difference operator is a Linear Operator
Let \(a_n\) and \(b_n\) be sequences, and let \(c\) be any number. Then
- \( \Delta (a_n+b_n)= \Delta a_n+ \Delta b_n\), and
- \( \Delta ( c a_n) =c \Delta a_n \).
- Proof
-
Very simple calculation.
Definition: Falling Powers
The falling power is denoted by \(x^{\underline{m}} \) and it is defined by \( x (x-1)(x-2)(x-3) \cdots (x-m+1)\), with \(x^{\underline{0}}=1\).
Falling powers are useful in the difference calculus because of the following property:
Theorem \(\PageIndex{2}\)
\( \Delta n^{\underline{m}} =m \,n^{\underline{m-1}} \).
- Proof
-
\( \Delta n^{\underline{m}}= (n+1)^{\underline{m}}-n^{\underline{m}} \)
\(=(n+1) n (n-1)(n-2)(n-3) \cdots (n-m+2)- n (n-1)(n-2)(n-3) \cdots (n-m+1)\)
\(=n (n-1)(n-2)(n-3) \cdots (n-m+2) ( (n+1)-(n-m+1))\)
\(= n (n-1)(n-2)(n-3) \cdots (n-m+2) \,m\)
\(=m\, n^{\underline{m-1}} \).
Let us now consider the sequence of numbers in the example \(\PageIndex{1}\).
| Number of points on the circle | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of regions | 1 | 1 | 2 | 4 | 8 | 16 | 31 | 57 | 99 |
| \(\Delta a_n\) | 0 | 1 | 2 | 4 | 8 | 15 | 26 | 42 | |
| \(\Delta^2 a_n\) | 1 | 1 | 2 | 4 | 7 | 11 | 16 | ||
| \(\Delta^3 a_n\) | 0 | 1 | 2 | 3 | 4 | 5 | |||
| \(\Delta^4 a_n\) | 1 | 1 | 1 | 1 | 1 |
Since the fourth difference is constant, \(a_n\) should be polynomial of degree \(4\). Let's explore how to find this polynomial.
Definition
\[ {n \choose k } =\displaystyle \frac{ n!}{k! (n-k)!} , k \leq n, n \in \mathbb{N} \cup \{0\} .\]
Theorem \(\PageIndex{2}\)
\[\Delta \displaystyle {n \choose k } = \displaystyle {n \choose k-1}, k \leq n, n \in \mathbb{N} \cup \{0\} .\]
- Proof
-
Note that \[ \displaystyle {n \choose k }= \frac{1}{k!} n^{\underline{k}}.\]
Consider \( \Delta {n \choose k } = \Delta ( \frac{1}{k!} n^{\underline{k}}) \)
\(= \frac{1}{k!} \Delta( n^{\underline{k}})\)
\( = \frac{k}{k!} n^{\underline{(k-1)}}\)
\(= \frac{1}{(k-1)!} n^{\underline{(k-1)}}\)
\(= {n \choose k-1}\).
We can also see this by considering Pascal’s triangle.
Theorem \(\PageIndex{3}\) Newton's formula
Let \(a_0, a_1, a_2, \cdots \) be sequence of numbers such that \(\Delta^{k+1} a_0=0. \) Then the \(n\) th term of the original sequence is given by
\[ a_n= \frac{1}{k!}(\Delta^k a_0)n^{\underline{k}} + \cdots+ a_0= a_0+ {n \choose 0 } \Delta a_1 +{n \choose 2 } \Delta^2 a_2+ \cdots + {n \choose k } \Delta^k a_k. \]
- Proof
-
Exercise.
If \(n\) th term of the original sequence is linear then the first difference will be a constant. If \(n\) th term of the original sequence is quadratic then the second difference will be a constant. A cubic sequence has the third difference constant.
Source
- Thanks to Olivia Nannan for the diagram.
- Reference: Kunin, George B. "The finite difference calculus and applications to the interpolation of sequences." MIT Undergraduate Journal of Mathematics 232.2001 (2001): 101-9.
- Reference: Samson, D. (2006). Number patterns, cautionary tales and finite differences. Learning and Teaching Mathematics, 2006(3), 3-8.


