1.2: One sided Limits and Vertical Asymptotes
- Page ID
- 10144
This page is a draft and is under active development.
One Sided Limits
We begin our exploration of limits by taking a look at the graphs of the following functions
- \(\displaystyle f(x)=x+1\)
- \(\displaystyle g(x)=\frac{x^2−1}{x−1}, x \ne 1\)
- \(h(x)= \left\{ \begin{array}{cc}
\displaystyle \frac{x^2−1}{x−1} & \mbox{ if } x\neq 1 \\
\\
0 & \mbox{ if } x=1 \\
\end{array}
\right.\)
which are shown in Figure \(\PageIndex{1}\). In particular, let’s focus our attention on the behavior of each graph at and around \(x=1\).
Example \(\PageIndex{1}\):
Consider, \(\displaystyle f(x)=x+1\)
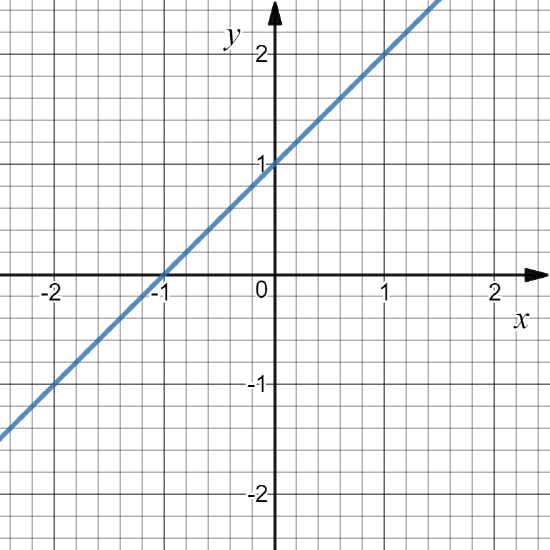
Evaluate \[\lim_{x \to 1}f(x).\]
\[\lim_{x \to 1}f(x)=2.\]
Example \(\PageIndex{2}\):
Consider, \(\displaystyle g(x)=\frac{x^2−1}{x−1}, x \ne 1\),
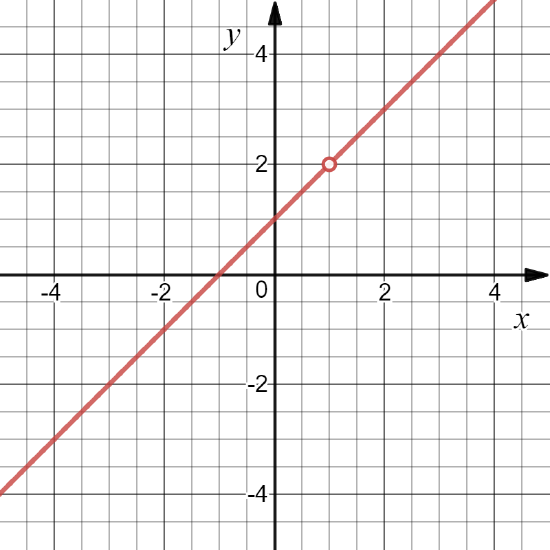
Evaluate \[\lim_{x \to 1}g(x).\]
\[\lim_{x \to 1}g(x)=2.\] See the figure above. Note that \(g(2)\) is undefined.
Example \(\PageIndex{3}\):
Consider, \(h(x)= \left\{ \begin{array}{cc}
\displaystyle \frac{x^2−1}{x−1} & \mbox{ if } x\neq 1 \\
\\
0 & \mbox{ if } x=1 \\
\end{array}
\right.\)
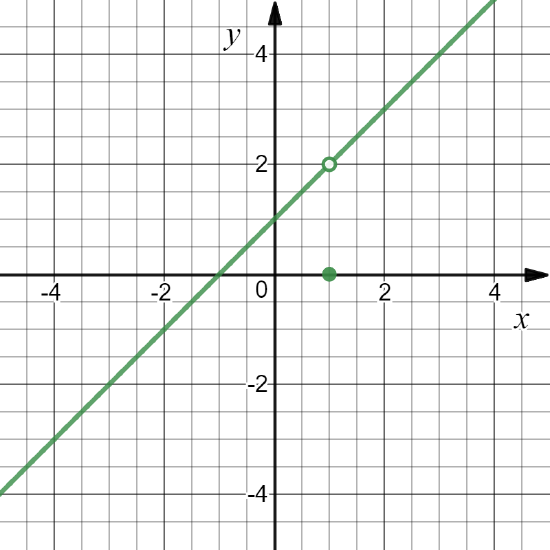
Evaluate \[\lim_{x \to 1}h(x).\]
\[\lim_{x \to 1}h(x)=2.\] See the figure above. Note that \(h(2)=0\).
We can now present an informal definition of one-sided limits.
Definition: One-sided Limits
We define two types of one-sided limits.
Limit from the left:
Let \(f(x)\) be a function defined at all values in an open interval of the form \(z\), and let \(L\) be a real number. If the values of the function \(f(x)\) approach the real number \(L\) as the values of \(x\) (where \(x<a\)) approach the number a, then we say that \(L\) is the limit of \(f(x)\) as \(x\) approaches a from the left. Symbolically, we express this idea as
\[\lim_{x \to a−}f(x)=L.\]
Limit from the right:
Let \(f(x)\) be a function defined at all values in an open interval of the form \((a,c)\), and let \(L\) be a real number. If the values of the function \(f(x)\) approach the real number \(L\) as the values of \(x\) (where \(x>a\)) approach the number \(a\), then we say that \(L\) is the limit of \(f(x)\) as x approaches a from the right. Symbolically, we express this idea as
\[\lim_{x \to a+}f(x)=L.\]Example \(\PageIndex{1}\)
Example \(\PageIndex{4}\): Evaluating One-Sided Limits
For the function \(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\), evaluate each of the following limits.
- \(\displaystyle \lim_{x \to 2^−}f(x)\)
- \(\displaystyle \lim_{x \to 2^+}f(x)\)
Solution
From Figure \(\PageIndex{7}\), we can conclude that a. \(\displaystyle \lim_{x \to 2^−}f(x)=3\) and b. \(\displaystyle \lim_{x \to 2^+}f(x)=0\). Therefore, the (two-sided) limit of \(f(x)\) does not exist at \(x=2\).
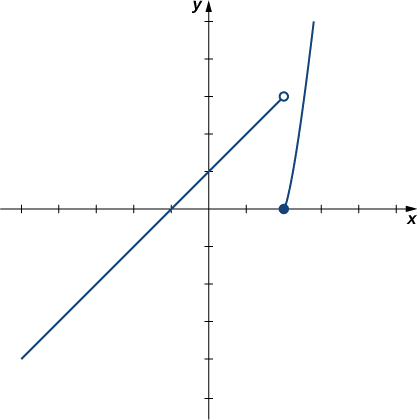
Example \(\PageIndex{4}\):
\(g(x)=\dfrac{|x−2|}{x−2}\)
(x-2).png?revision=1&size=bestfit&width=300&height=300)
Let us now consider the relationship between the limit of a function at a point and the limits from the right and left at that point. It seems clear that if the limit from the right and the limit from the left have a common value, then that common value is the limit of the function at that point. Similarly, if the limit from the left and the limit from the right take on different values, the limit of the function does not exist. These conclusions are summarized in Note.
Relating One-Sided and Two-Sided Limits
Let \(f(x)\) be a function defined at all values in an open interval containing \(a\), with the possible exception of \(a\) itself, and let \(L\) be a real number. Then,
\[\lim_{x \to a}f(x)=L\]
if and only if \(\displaystyle \lim_{x \to a^−}f(x)=L\) and \(\displaystyle \lim_{x \to a^+} f(x)=L\).
App: Intuitive Notion of the Limit
(You can change the values by dragging)
Infinite Limits
Evaluating the limit of a function at a point or evaluating the limit of a function from the right and left at a point helps us to characterize the behavior of a function around a given value. As we shall see, we can also describe the behavior of functions that do not have finite limits.
We now turn our attention to \(h(x)=1/(x−2)^2\), the third and final function introduced at the beginning of this section (see Figure \(\PageIndex{1}\)(c)). From its graph we see that as the values of \(x\) approach \(2\), the values of \(h(x)=1/(x−2)^2\) become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of \(h(x)\) as \(x\) approaches \(2\) is positive infinity. Symbolically, we express this idea as
\[\lim_{x \to 2}h(x)=+∞. \nonumber\]
More generally, we define infinite limits as follows:
Definitions: Infinite Limits
We define three types of infinite limits.
Infinite limits from the left: Let \(f(x)\) be a function defined at all values in an open interval of the form \((b,a)\).
i. If the values of \(f(x)\) increase without bound as the values of \(x\) (where \(x<a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) from the left is positive infinity and we write \[\lim_{x \to a^−}f(x)=+∞.\]
ii. If the values of \(f(x)\) decrease without bound as the values of \(x\) (where \(x<a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) from the left is negative infinity and we write \[\lim_{x \to a^−}f(x)=−∞.\]
Infinite limits from the right: Let \(f(x)\) be a function defined at all values in an open interval of the form \((a,c)\).
i. If the values of \(f(x)\) increase without bound as the values of \(x\) (where \(x>a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) from the left is positive infinity and we write \[\lim_{x \to a^+}f(x)=+∞.\]
ii. If the values of \(f(x)\) decrease without bound as the values of \(x\) (where \(x>a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) from the left is negative infinity and we write \[\lim_{x \to a^+}f(x)=−∞.\]
Two-sided infinite limit: Let \(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\)
i. If the values of \(f(x)\) increase without bound as the values of \(x\) (where \(x≠a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) is positive infinity and we write \[\lim_{x \to a} f(x)=+∞.\]
ii. If the values of \(f(x)\) decrease without bound as the values of \(x\) (where \(x≠a\)) approach the number \(a\), then we say that the limit as \(x\) approaches \(a\) is negative infinity and we write \[\lim_{x \to a}f(x)=−∞.\]
It is important to understand that when we write statements such as \(\displaystyle \lim_{x \to a}f(x)=+∞\) or \(\displaystyle \lim_{x \to a}f(x)=−∞\) we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists. For the limit of a function \(f(x)\) to exist at \(a\), it must approach a real number \(L\) as \(x\) approaches \(a\). That said, if, for example, \(\displaystyle \lim_{x \to a}f(x)=+∞\), we always write \(\displaystyle \lim_{x \to a}f(x)=+∞\) rather than \(\displaystyle \lim_{x \to a}f(x)\) DNE.
Example \(\PageIndex{5}\): Recognizing an Infinite Limit
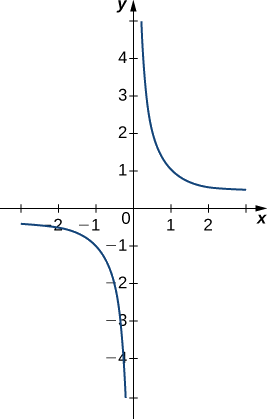
Evaluate each of the following limits, if possible. Use a table of functional values and graph \(f(x)=1/x\) to confirm your conclusion.
- \(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
- \(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
- \( \displaystyle \lim_{x \to 0}\frac{1}{x}\)
Solution
Begin by constructing a table of functional values.
| \(x\) | \(\dfrac{1}{x}\) | \(x\) | \(\dfrac{1}{x}\) |
|---|---|---|---|
| -0.1 | -10 | 0.1 | 10 |
| -0.01 | -100 | 0.01 | 100 |
| -0.001 | -1000 | 0.001 | 1000 |
| -0.0001 | -10,000 | 0.0001 | 10,000 |
| -0.00001 | -100,000 | 0.00001 | 100,000 |
| -0.000001 | -1,000,000 | 0.000001 | 1,000,000 |
a. The values of \(1/x\) decrease without bound as \(x\) approaches \(0\) from the left. We conclude that
\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber\]
b. The values of \(1/x\) increase without bound as \(x\) approaches \(0\) from the right. We conclude that
\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber\]
c. Since \(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) and \(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) have different values, we conclude that
\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber\]
The graph of \(f(x)=1/x\) in Figure \(\PageIndex{8}\) confirms these conclusions.
Exercise \(\PageIndex{5}\)
Evaluate each of the following limits, if possible. Use a table of functional values and graph \(f(x)=1/x^2\) to confirm your conclusion.
- \(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
- \(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)
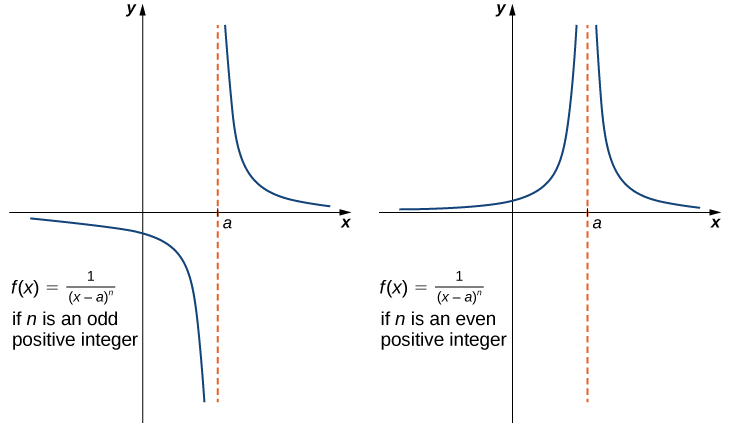
Infinite Limits from Positive Integers
If \(n\) is a positive even integer, then
\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1}\]
If \(n\) is a positive odd integer, then
\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2}\]
and
\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3}\]
We should also point out that in the graphs of \(f(x)=1/(x−a)^n\), points on the graph having \(x\)-coordinates very near to a are very close to the vertical line \(x=a\). That is, as \(x\) approaches \(a\), the points on the graph of \(f(x)\) are closer to the line \(x=a\). The line \(x=a\) is called a vertical asymptote of the graph. We formally define a vertical asymptote as follows:
Definition: Vertical Asymptotes
Let \(f(x)\) be a function. If any of the following conditions hold, then the line \(x=a\) is a vertical asymptote of \(f(x)\).
\[\lim_{x \to a^−}f(x)=+∞\]
\[\lim_{x \to a^−}f(x)=−∞\]
\[\lim_{x \to a^+}f(x)=+∞\]
\[\lim_{x \to a^+}f(x)=−∞\]
\[\lim_{x \to a}f(x)=+∞\]
\[\lim_{x \to a}f(x)=−∞\]
Example \(\PageIndex{6}\): Finding a Vertical Asymptote
Evaluate each of the following limits using Equations \ref{infLim1}, \ref{infLim2}, and \ref{infLim3} above. Identify any vertical asymptotes of the function \(f(x)=1/(x+3)^4.\)
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)
Solution
We can use the above equations directly.
- \(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
- \(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)
The function \(f(x)=1/(x+3)^4\) has a vertical asymptote of \(x=−3\).
Exercise \(\PageIndex{6}\)
Evaluate each of the following limits. Identify any vertical asymptotes of the function \(f(x)=\dfrac{1}{(x−2)^3}\).
- \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
- \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)
- Answer a
-
\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
- Answer b
-
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
- Answer c
-
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\) DNE. The line \(x=2\) is the vertical asymptote of \(f(x)=1/(x−2)^3.\)
In the next example we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.
Example \(\PageIndex{7}\): Behavior of a Function at Different Points
Use the graph of \(f(x)\) in Figure \(\PageIndex{10}\) to determine each of the following values:
- \(\displaystyle \lim_{x \to −4^−}f(x)\); \(\displaystyle \lim_{x \to −4^+}f(x)\); \(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
- \(\displaystyle \lim_{x \to −2^−}f(x\)); \(\displaystyle \lim_{x \to −2^+}f(x)\); \(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
- \( \displaystyle \lim_{x \to 1^−}f(x)\); \(\displaystyle \lim_{x \to 1^+}f(x)\); \(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
- \( \displaystyle \lim_{x \to 3^−}f(x)\); \(\displaystyle \lim_{x \to 3^+}f(x)\); \(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)
![The graph of a function f(x) described by the above limits and values. There is a smooth curve for values below x=-2; at (-2, 3), there is an open circle. There is a smooth curve between (-2, 1] with a closed circle at (1,6). There is an open circle at (1,3), and a smooth curve stretching from there down asymptotically to negative infinity along x=3. The function also curves asymptotically along x=3 on the other side, also stretching to negative infinity. The function then changes concavity in the first quadrant around y=4.5 and continues up.](https://math.libretexts.org/@api/deki/files/7969/imageedit_30_9857663504.png?revision=1)
Solution
Using the definitions above and the graph for reference, we arrive at the following values:
- \(\displaystyle \lim_{x \to −4^−}f(x)=0\); \(\displaystyle \lim_{x \to −4^+}f(x)=0\); \(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
- \(\displaystyle \lim_{x \to −2^−}f(x)=3\); \(\displaystyle \lim_{x \to −2^+}f(x)=3\); \(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) is undefined
- \(\displaystyle \lim_{x \to 1^−}f(x)=6\); \(\displaystyle \lim_{x \to 1^+}f(x)=3\); \(\displaystyle \lim_{x \to 1}f(x)\) DNE; \(f(1)=6\)
- \(\displaystyle \lim_{x \to 3^−}f(x)=−∞\); \(\displaystyle \lim_{x \to 3^+}f(x)=−∞\); \(\displaystyle \lim_{x \to 3}f(x)=−∞\); \(f(3)\) is undefined
Exercise \(\PageIndex{7}\)
Evaluate \(\displaystyle\lim_{x \to 1}f(x)\) for \(f(x)\) shown here:
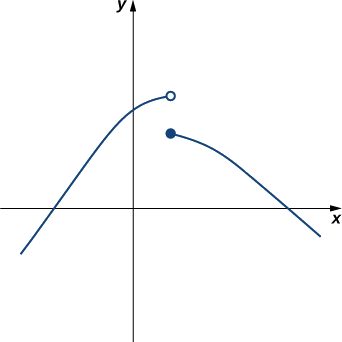
- Hint
-
Compare the limit from the right with the limit from the left.
- Answer
-
\(\displaystyle\lim_{x \to 1}f(x)\) does not exist
Example \(\PageIndex{8}\): Einstein’s Equation
In the Chapter opener we mentioned briefly how Albert Einstein showed that a limit exists to how fast any object can travel. Given Einstein’s equation for the mass of a moving object
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber\]
what is the value of this bound?

Solution
Our starting point is Einstein’s equation for the mass of a moving object,
\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber\]
where \(m_0\) is the object’s mass at rest, \(v\) is its speed, and \(c\) is the speed of light. To see how the mass changes at high speeds, we can graph the ratio of masses \(m/m_0\) as a function of the ratio of speeds, \(v/c\) (Figure \(\PageIndex{13}\)).
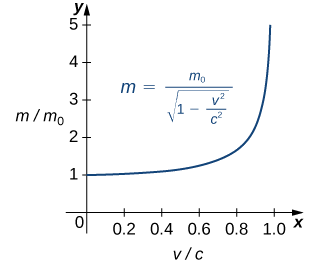
We can see that as the ratio of speeds approaches 1—that is, as the speed of the object approaches the speed of light—the ratio of masses increases without bound. In other words, the function has a vertical asymptote at \(v/c=1\). We can try a few values of this ratio to test this idea.
| \(v/c\) | \(\sqrt{1-\frac{v^2}{c^2}}\) | \(m/m_o\) |
|---|---|---|
| 0.99 | 0.1411 | 7.089 |
| 0.999 | 0.0447 | 22.37 |
| 0.9999 | 0.0141 | 70.7 |
Thus, according to Table \(\PageIndex{8}\):, if an object with mass 100 kg is traveling at 0.9999c, its mass becomes 7071 kg. Since no object can have an infinite mass, we conclude that no object can travel at or more than the speed of light.
Key Concepts
- A table of values or graph may be used to estimate a limit.
- If the limit of a function at a point does not exist, it is still possible that the limits from the left and right at that point may exist.
- If the limits of a function from the left and right exist and are equal, then the limit of the function is that common value.
- We may use limits to describe infinite behavior of a function at a point.
Key Equations
- Intuitive Definition of the Limit
\(\displaystyle \lim_{x \to a}f(x)=L\)
- Two Important Limits
\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)
- One-Sided Limits
\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)
- Infinite Limits from the Left
\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)
- Infinite Limits from the Right
\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)
- Two-Sided Infinite Limits
\(\displaystyle \lim_{x \to a}f(x)=+∞\): \(\displaystyle \lim_{x \to a^−}f(x)=+∞\) and \(\displaystyle \lim_{x \to a^+} f(x)=+∞\)
\(\displaystyle \lim_{x \to a}f(x)=−∞\): \(\displaystyle \lim_{x \to a^−}f(x)=−∞\) and \(\displaystyle \lim_{x \to a^+} f(x)=−∞\)
Glossary
- infinite limit
- A function has an infinite limit at a point a if it either increases or decreases without bound as it approaches a
- intuitive definition of the limit
- If all values of the function \(f(x)\) approach the real number L as the values of \(x(≠a)\) approach a, \(f(x)\) approaches L
- one-sided limit
- A one-sided limit of a function is a limit taken from either the left or the right
- vertical asymptote
- A function has a vertical asymptote at \(x=a\) if the limit as x approaches a from the right or left is infinite
Source
- Calculus Applets using GeoGebra by Marc Renault is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)


Follow the procedures from Example \(\PageIndex{4}\).
a. \(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\);
b. \(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\);
c. \(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)
It is useful to point out that functions of the form \(f(x)=1/(x−a)^n\), where n is a positive integer, have infinite limits as \(x\) approaches \(a\) from either the left or right (Figure \(\PageIndex{9}\)). These limits are summarized in the above definitions.