2.0E: Exercises
- Page ID
- 10629
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
For the following exercises, use the equation to find the slope of the secant line between the values \(x_1\) and \(x_2\) for each function \(y=f(x)\).
1) \(f(x)=4x+7; x_1=2,x_2=5\)
2) \(f(x)=8x−3;x_1=−1,x_2=3\)
3) \(f(x)=x^2+2x+1;x_1=3,x_2=3.5\)
4) \(f(x)=−x^2+x+2;x_1=0.5,x_2=1.5\)
5) \(f(x)=\frac{4}{3x−1};x_1=1,x_2=3\)
6) \(f(x)=\frac{x−7}{2x+1};x_1=−2,x_2=0\)
7) \(f(x)=\sqrt{x};x_1=1,x_2=16\)
8) \(f(x)=\sqrt{x−9};x_1=10,x_2=13\)
9) \(f(x)=x^{1/3}+1;x_1=0,x_2=8\)
10) \(f(x)=6x^{2/3}+2x^{1/3};x_1=1,x_2=27\)
- Answers to odd numbered questions
-
1. \(4\)
3. \(8.5\)
5. \(−\frac{3}{4}\)
7. \(0.2\)
9. 0.25
Exercise \(\PageIndex{2}\)
For the following exercises, use Equation to find the slope of the secant line between the values \(x_1\) and \(x_2\) for each function \
For the following functions,
a. use Equation to find the slope of the tangent line \(m_{tan}=f′(a)\), and
b. find the equation of the tangent line to \(f\) at \(x=a\).
1) \(f(x)=3−4x,a=2\)
2) \(f(x)=\frac{x}{5}+6,a=−1\)
3) \(f(x)=x^2+x,a=1\)
4) \(f(x)=1−x−x^2, a=0\)
5) \(f(x)=\frac{7}{x},a=3\)
6) \(f(x)=\sqrt{x+8},a=1\)
7) \(f(x)=2−3x^2,a=−2\)
8) \(f(x)=\frac{−3}{x−1},a=4\)
9) \(f(x)=\frac{2}{x+3},a=−4\)
10) \(f(x)=\frac{3}{x^2},a=3\)
- Answers to odd numbered questions
-
1. \(a. −4\) \(b. y=3−4x\)
3. \(a. 3\) \(b. y=3x−1\)
5. \(a. \frac{−7}{9}\) \(b. y=\frac{−7}{9}x+\frac{14}{3}\)
7. \(a. 12 b. y=12x+14\)
9. \(a. −2 b. y=−2x−10\)
Exercise \(\PageIndex{3}\)
For the following functions \(y=f(x)\), find \(f′(a)\) using Equation.
1) \(f(x)=5x+4,a=−1\)
2) \(f(x)=−7x+1,a=3\)
3) \(f(x)=x^2+9x,a=2\)
4) \(f(x)=3x^2−x+2,a=1\)
5) \(f(x)=\sqrt{x},a=4\)
6) \(f(x)=\sqrt{x−2},a=6\)
7) \(f(x)=\frac{1}{x},a=2\)
8) \(f(x)=\frac{1}{x−3},a=−1\)
9) \(f(x)=\frac{1}{x^3},a=1\)
10) \(f(x)=\frac{1}{\sqrt{x}},a=4\)
- Answers to odd numbered questions
-
1. \(5\)
3. \(13\)
5. \(\frac{1}{4}\)
7. \(-\frac{1}{4}\)
9. \(−3\)
Exercise \(\PageIndex{4}\)
For the following exercises, given the function \(y=f(x)\),
a. find the slope of the secant line \(PQ\) for each point \(Q(x,f(x))\) with \(x\) value given in the table.
b. Use the answers from a. to estimate the value of the slope of the tangent line at \(P\).
c. Use the answer from b. to find the equation of the tangent line to \(f\) at point \(P\).
1) \(f(x)=x^2+3x+4\), \(P(1,8)\) (Round to \(6\) decimal places.)
| \(x\) | Slope \(m_{PQ}\) | \(x\) | Slope \(m_{PQ}\) |
| 1.1 | (i) | 0.9 | (vii) |
| 1.01 | (ii) | 0.99 | (viii) |
| 1.001 | (iii) | 0.999 | (ix) |
| 1.0001 | (iv) | 0.9999 | (x) |
| 1.00001 | (v) | 0.99999 | (xi) |
| 1.000001 | (vi) | 0.999999 | (xii) |
2) \(f(x)=\frac{x+1}{x^2−1},P(0,−1)\)
| \(x\) | \(Slope m_{PQ}\) | \(x\) | \(Slope m_{PQ}\) |
| 0.1 | (i) | −0.1 | (vii) |
| 0.01 | (ii) | −0.01 | (viii) |
| 0.001 | (iii) | −0.001 | (ix) |
| 0.0001 | (iv) | −0.0001 | (x) |
| 0.00001 | (v) | −0.00001 | (xi) |
| 0.000001 | (vi) | −0.000001 | (xii) |
3) \(f(x)=10e^{0.5x}\), \(P(0,10)\) (Round to \(4\) decimal places.)
| \(x\) | Slope \(m_{PQ}\) |
| −0.1 | (i) |
| −0.01 | (ii) |
| −0.001 | (iii) |
| −0.0001 | (iv) |
| −0.00001 | (v) |
| −0.000001 | (vi) |
4) \(f(x)=tan(x)\), \(P(π,0)\)
| \(x\) | Slope \(m_{PQ}\) |
| 3.1 | (i) |
| 3.14 | (ii) |
| 3.141 | (iii) |
| 3.1415 | (iv) |
| 3.14159 | (v) |
| 3.141592 | (vi) |
- Answers to odd numbered questions
-
1. a. \((i)5.100000, (ii)5.010000, (iii)5.001000, (iv)5.000100, (v)5.000010, (vi)5.000001, (vii)4.900000, (viii)4.990000, (ix)4.999000, (x)4.999900, (xi)4.999990, (x)4.999999\)
b. \(m_{tan}=5\)
c. \(y=5x+3\)
3. a. \( (i)4.8771, (ii)4.9875(iii)4.9988, (iv)4.9999, (v)4.9999, (vi)4.9999 \)
b. \(m_{tan}=5\)
c. \(y=5x+10\)
Exercise \(\PageIndex{5}\)
For the following position functions \(y=s(t)\), an object is moving along a straight line, where \(t\) is in seconds and \(s\) is in meters. Find
a. the simplified expression for the average velocity from \(t=2\) to \(t=2+h\);
b. the average velocity between \(t=2\) and \(t=2+h\), where \((i)h=0.1, (ii)h=0.01, (iii)h=0.001\), and \((iv)h=0.0001\); and
c. use the answer from a. to estimate the instantaneous velocity at \(t=2\) second.
1) \(s(t)=\frac{1}{3}t+5\)
2) \(s(t)=t^2−2t\)
3) \(s(t)=2t^3+3\)
4) \(s(t)=\frac{16}{t^2}−\frac{4}{t}\)
- Answers to odd numbered questions
-
1. a. \( \frac{1}{3}\);
b. \((i)0.3\) m/s, \((ii)0.3\) m/s, \((iii)0.3\) m/s, \((iv)0.3\) m/s;
c. \(0.3=13\) m/s
3. a. \(2(h^2+6h+12)\);
b. \((i)25.22 m/s, (ii)24.12 m/s, (iii)24.01 m/s, (iv)24 m/s;
c. 24 m/s\)
Exercise \(\PageIndex{6}\)
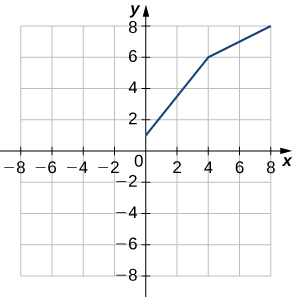
1) Use the following graph to evaluate a. \(f′(1)\) and b. \(f′(6).\)
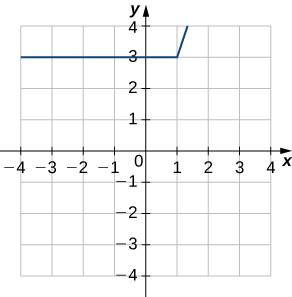
2) Use the following graph to evaluate a. \(f′(−3)\) and b. \(f′(1.5)\).
- Answer
-
1. a. \(1.25\)
b. \(0.5\)
Exercise \(\PageIndex{7}\)
For the following exercises, use the limit definition of derivative to show that the derivative does not exist at x=a for each of the given functions.
1) \(f(x)=x^{1/3}, x=0\)
2) \(f(x)=x^{2/3},x=0\)
3) \(f(x)=\begin{cases}1 & x<1\\x & x≥1\end{cases}, x=1\)
4) \(f(x)=\frac{|x|}{x},x=0\)
- Answers to odd numbered questions
-
1. \(lim_{x→0^−}\frac{x^{1/3}−0}{x−0}=lim_{x→0^−}\frac{1}{x^{2/3}}=∞\),
3. \(lim_{x→1^−}\frac{1−1}{x−1}=0≠1=lim_{x→1^+}\frac{x−1}{x−1}\)
Exercise \(\PageIndex{8}\)
The position in feet of a race car along a straight track after \(t\) seconds is modeled by the function \(s(t)=8t^2−\frac{1}{16}t^3.\)
a. Find the average velocity of the vehicle over the following time intervals to four decimal places:
i. [\(4, 4.1\)]
ii. [\(4, 4.01\)]
iii. [\(4, 4.001\)]
iv. [\(4, 4.0001\)]
b. Use a. to draw a conclusion about the instantaneous velocity of the vehicle at \(t=4\) seconds.
- Answer
-
a. \((i)61.7244 ft/s, (ii)61.0725 ft/s (iii)61.0072 ft/s (iv)61.0007 ft/s\)
b. At \(4\) seconds the race car is traveling at a rate/velocity of \(61\) ft/s.
Exercise \(\PageIndex{9}\)
The distance in feet that a ball rolls down an incline is modeled by the function \(s(t)=14t^2\),
where t is seconds after the ball begins rolling.
a. Find the average velocity of the ball over the following time intervals:
i. [5, 5.1]
ii. [5, 5.01]
iii. [5, 5.001]
iv. [5, 5.0001]
b. Use the answers from a. to draw a conclusion about the instantaneous velocity of the ball at \(t=5\) seconds.
- Answer
-
Under Construction
Exercise \(\PageIndex{10}\)
Two vehicles start out traveling side by side along a straight road. Their position functions, shown in the following graph, are given by \(s=f(t)\) and \(s=g(t)\), where s is measured in feet and t is measured in seconds.
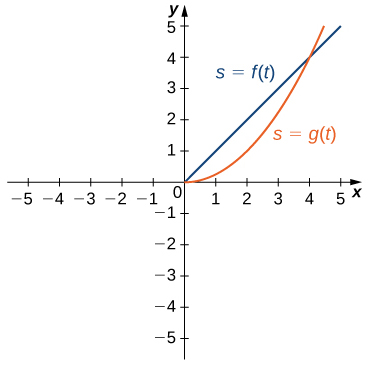
a. Which vehicle has traveled farther at \(t=2\) seconds?
b. What is the approximate velocity of each vehicle at \(t=3\) seconds?
c. Which vehicle is traveling faster at \(t=4\) seconds?
d. What is true about the positions of the vehicles at \(t=4\) seconds?
- Answer
-
a. The vehicle represented by \(f(t)\), because it has traveled \(2\) feet, whereas \(g(t)\) has traveled \(1\) foot.
b. The velocity of \(f(t)\) is constant at \(1\) ft/s, while the velocity of g(t) is approximately \(2\) ft/s.
c. The vehicle represented by \(g(t)\), with a velocity of approximately \(4\) ft/s. d. Both have traveled \(4\) feet in \(4\) seconds.
Exercise \(\PageIndex{11}\)
The total cost \(C(x)\), in hundreds of dollars, to produce \(x\) jars of mayonnaise is given by \(C(x)=0.000003x^3+4x+300\).
a. Calculate the average cost per jar over the following intervals:
i. [100, 100.1]
ii. [100, 100.01]
iii. [100, 100.001]
iv. [100, 100.0001]
b. Use the answers from a. to estimate the average cost to produce \(100\) jars of mayonnaise.
- Answer
-
Under Construction
Exercise \(\PageIndex{12}\)
For the function \(f(x)=x^3−2x^2−11x+12\), do the following.
a. Use a graphing calculator to graph f in an appropriate viewing window.
b. Use the ZOOM feature on the calculator to approximate the two values of \(x=a\) for which \(m_{tan}=f′(a)=0\).
- Answer
-
a.
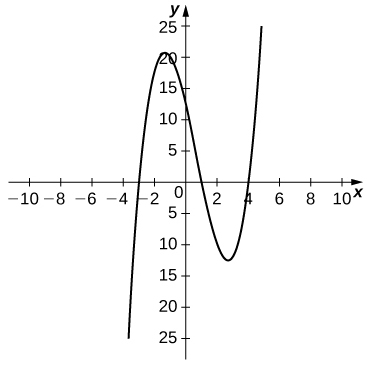
b. \(a≈−1.361,2.694\)
Exercise \(\PageIndex{13}\)
For the function \(f(x)=\frac{x}{1+x^2}\), do the following.
a. Use a graphing calculator to graph f in an appropriate viewing window.
b. Use the ZOOM feature on the calculator to approximate the values of \(x=a\) for which \(m_{tan}=f′(a)=0\).
- Answer
-
Under Construction
Exercise \(\PageIndex{14}\)
Suppose that \(N(x)\) computes the number of gallons of gas used by a vehicle traveling \(x\) miles. Suppose the vehicle gets \(30\) mpg.
a. Find a mathematical expression for \(N(x)\).
b. What is \(N(100)\)? Explain the physical meaning.
c. What is \(N′(100)\)? Explain the physical meaning.
- Answer
-
a. \(N(x)=\frac{x}{30}\)
b. ∼\(3.3\) gallons. When the vehicle travels \(100\) miles, it has used \(3.3\) gallons of gas.
c. \(\frac{1}{30}\). The rate of gas consumption in gallons per mile that the vehicle is achieving after having traveled \(100\) miles.
Exercise \(\PageIndex{15}\)
For the function \(f(x)=x^4−5x^2+4\), do the following.
a. Use a graphing calculator to graph \(f\) in an appropriate viewing window.
b. Use the \(nDeriv\) function, which numerically finds the derivative, on a graphing calculator to estimate \(f′(−2),f′(−0.5),f′(1.7)\), and \(f′(2.718)\).
- Answer
-
Under Construction
Exercise \(\PageIndex{16}\)
For the function \(f(x)=\frac{x^2}{x^2+1}\), do the following.
a. Use a graphing calculator to graph \(f\) in an appropriate viewing window.
b. Use the \(nDeriv\) function on a graphing calculator to find \(f′(−4),f′(−2),f′(2)\), and \(f′(4)\).
- Answer
-
a.
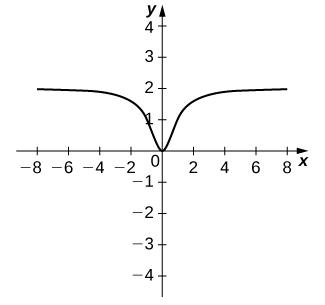
b. \(−0.028,−0.16,0.16,0.028\)
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

