3.1: Related Rates
- Page ID
- 10301
This page is a draft and is under active development.
We have seen that for quantities that are changing over time, the rates at which these quantities change are given by derivatives. If two related quantities are changing over time, the rates at which the quantities change are related. For example, if a balloon is being filled with air, both the radius of the balloon and the volume of the balloon are increasing. In this section, we consider several problems in which two or more related quantities are changing and we study how to determine the relationship between the rates of change of these quantities.
Setting up Related-Rates Problems
Example \(\PageIndex{1}\):
An object is moving in the clockwise direction around the unit circle \(x^2+y^2=1.\) As it passes through the point \(\left(\displaystyle \frac{1}{\sqrt{2}},\displaystyle \frac{1}{\sqrt{2}} \right)\), its \(y-\)coordinate is decreasing at the rate of \(4\) units per second. At what rate is the \(x-\)coordinate changing at this point.
Solution
Exercise \(\PageIndex{1}\)
An object is moving in the clockwise direction around the unit circle \(x^2+y^2=1.\) As it passes through the point \(\left(\displaystyle \frac{1}{\sqrt{2}},\displaystyle \frac{-1}{\sqrt{2}} \right)\), its \(y-\)coordinate is decreasing at the rate of \(4\) units per second. At what rate is the \(x-\)coordinate changing at this point.
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
In many real-world applications, related quantities are changing with respect to time. For example, if we consider the balloon example again, we can say that the rate of change in the volume, \(V\), is related to the rate of change in the radius, \(r\). In this case, we say that \(\frac{dV}{dt}\) and \(\frac{dr}{dt}\) are related rates because \(V\) is related to r. Here we study several examples of related quantities that are changing with respect to time and we look at how to calculate one rate of change given another rate of change.
Example \(\PageIndex{2}\): Inflating a Balloon
A spherical balloon is being filled with air at a constant rate of \(2cm^3/sec\) (Figure). How fast is the radius increasing when the radius is \(3cm\)?
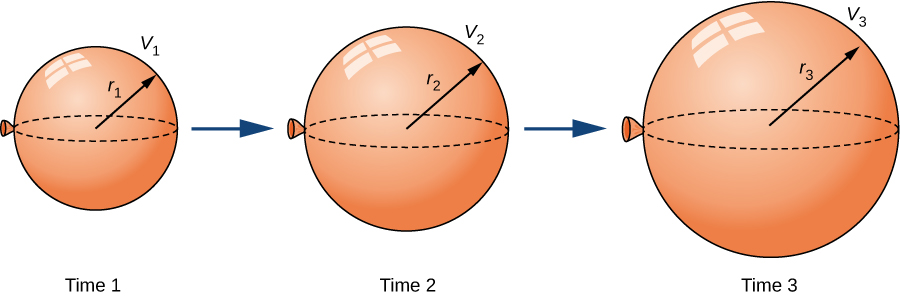
Solution
The volume of a sphere of radius \(r\) centimeters is
\(V=\frac{4}{3}πr^3cm^3.\)
Since the balloon is being filled with air, both the volume and the radius are functions of time. Therefore, \(t\) seconds after beginning to fill the balloon with air, the volume of air in the balloon is
\(V(t)=\frac{4}{3}π[r(t)]^3cm^3.\)
Differentiating both sides of this equation with respect to time and applying the chain rule, we see that the rate of change in the volume is related to the rate of change in the radius by the equation
\(V'(t)=4π[r(t)]^2r′(t).\)
The balloon is being filled with air at the constant rate of 2 cm3/sec, so \(V'(t)=2cm^3/sec.\) Therefore,
\(2cm^3/sec=(4π[r(t)]^2cm^2)⋅(r'(t)cm/s),\)
which implies
\(r'(t)=\frac{1}{2π[r(t)]^2}cm/sec\).
When the radius \(r=3cm,\)
\(r'(t)=\frac{1}{18π}cm/sec.\)
Exercise \(\PageIndex{2}\)
What is the instantaneous rate of change of the radius when \(r=6cm\)?
- Solution
-
\\(\frac{dr}{dt}=\frac{1}{2πr^2}\)
- Answer
-
\(\frac{1}{72π}cm/sec\), or approximately 0.0044 cm/sec
Before looking at other examples, let’s outline the problem-solving strategy we will be using to solve related-rates problems.
Problem-Solving Strategy: Solving a Related-Rates Problem
- Assign symbols to all variables involved in the problem. Draw a figure if applicable.
- State, in terms of the variables, the information that is given and the rate to be determined.
- Find an equation relating the variables introduced in step 1.
- Using the chain rule, differentiate both sides of the equation found in step 3 with respect to the independent variable. This new equation will relate the derivatives.
- Substitute all known values into the equation from step 4, then solve for the unknown rate of change
Note that when solving a related-rates problem, it is crucial not to substitute known values too soon. For example, if the value for a changing quantity is substituted into an equation before both sides of the equation are differentiated, then that quantity will behave as a constant and its derivative will not appear in the new equation found in step 4. We examine this potential error in the following example.
Examples of the Process
Let’s now implement the strategy just described to solve several related-rates problems. The first example involves a plane flying overhead. The relationship we are studying is between the speed of the plane and the rate at which the distance between the plane and a person on the ground is changing.
Example \(\PageIndex{3}\): An Airplane Flying at a Constant Elevation
An airplane is flying overhead at a constant elevation of \(4000ft\). A man is viewing the plane from a position \(3000ft\) from the base of a radio tower. The airplane is flying horizontally away from the man. If the plane is flying at the rate of \(600ft/sec\), at what rate is the distance between the man and the plane increasing when the plane passes over the radio tower?
Solution: Step 1. Draw a picture, introducing variables to represent the different quantities involved.
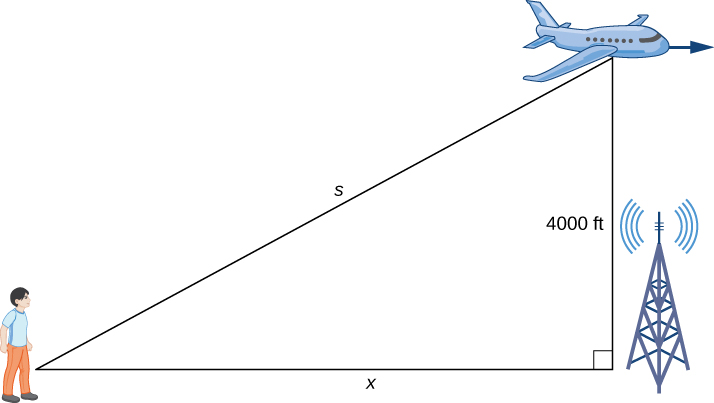
As shown, \(x\) denotes the distance between the man and the position on the ground directly below the airplane. The variable \(s\) denotes the distance between the man and the plane. Note that both \(x\) and \(s\) are functions of time. We do not introduce a variable for the height of the plane because it remains at a constant elevation of \(4000ft\). Since an object’s height above the ground is measured as the shortest distance between the object and the ground, the line segment of length 4000 ft is perpendicular to the line segment of length \(x\) feet, creating a right triangle.
Step 2. Since \(x\) denotes the horizontal distance between the man and the point on the ground below the plane, \(dx/dt\) represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore, \(\frac{dx}{dt}=600\) ft/sec. Since we are asked to find the rate of change in the distance between the man and the plane when the plane is directly above the radio tower, we need to find \(ds/dt\) when \(x=3000ft.\)
Step 3. From the figure, we can use the Pythagorean theorem to write an equation relating \(x\) and \(s\):
\([x(t)]^2+4000^2=[s(t)]^2.\)
Step 4. Differentiating this equation with respect to time and using the fact that the derivative of a constant is zero, we arrive at the equation
\(x\frac{dx}{dt}=s\frac{ds}{dt}.\)
Step 5. Find the rate at which the distance between the man and the plane is increasing when the plane is directly over the radio tower. That is, find \(\frac{ds}{dt}\) when \(x=3000ft\). Since the speed of the plane is \(600ft/sec\), we know that \(\frac{dx}{dt}=600ft/sec\). We are not given an explicit value for \(s\); however, since we are trying to find \(\frac{ds}{dt}\) when \(x=3000ft\), we can use the Pythagorean theorem to determine the distance \(s\) when \(x=3000\) and the height is \(4000ft\). Solving the equation
\(3000^2+4000^2=s^2\)
for \(s\), we have \(s=5000ft\) at the time of interest. Using these values, we conclude that \(ds/dt\)
is a solution of the equation
\((3000)(600)=(5000)⋅\frac{ds}{dt}\).
Therefore,
\(\frac{ds}{dt}=\frac{3000⋅600}{5000}=360ft/sec.\)
Note: When solving related-rates problems, it is important not to substitute values for the variables too soon. For example, in step 3, we related the variable quantities \(x(t)\) and \(s(t)\) by the equation
\([x(t)]^2+4000^2=[s(t)]^2.\)
Since the plane remains at a constant height, it is not necessary to introduce a variable for the height, and we are allowed to use the constant 4000 to denote that quantity. However, the other two quantities are changing. If we mistakenly substituted \(x(t)=3000\) into the equation before differentiating, our equation would have been
\(3000^2+4000^2=[s(t)]^2.\)
After differentiating, our equation would become
\(0=s(t)\frac{ds}{dt}.\)
As a result, we would incorrectly conclude that \(\frac{ds}{dt}=0.\)
Exercise \(\PageIndex{3}\)
What is the speed of the plane if the distance between the person and the plane is increasing at the rate of \(300ft/sec\)?
- Hint
-
\(\frac{ds}{dt}=300ft/sec\)
- Answer
-
\(500ft/sec\)
We now return to the problem involving the rocket launch from the beginning of the chapter.
Example \(\PageIndex{4}\): Chapter Opener - A Rocket Launch

A rocket is launched so that it rises vertically. A camera is positioned \(5000ft\) from the launch pad. When the rocket is \(1000ft\) above the launch pad, its velocity is \(600ft/sec.\) Find the necessary rate of change of the camera’s angle as a function of time so that it stays focused on the rocket.
Solution: Step 1. Draw a picture introducing the variables.
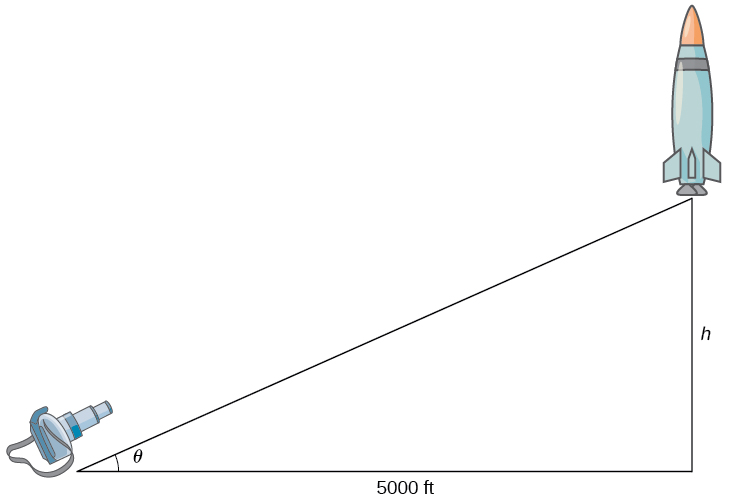
Let \(h\) denote the height of the rocket above the launch pad and \(θ\) be the angle between the camera lens and the ground.
Step 2. We are trying to find the rate of change in the angle of the camera with respect to time when the rocket is 1000 ft off the ground. That is, we need to find \(\frac{dθ}{dt}\) when \(h=1000ft\). At that time, we know the velocity of the rocket is \(\frac{dh}{dt}=600ft/sec.\)
Step 3. Now we need to find an equation relating the two quantities that are changing with respect to time: \(h\) and \(θ\). How can we create such an equation? Using the fact that we have drawn a right triangle, it is natural to think about trigonometric functions. Recall that \(tanθ\) is the ratio of the length of the opposite side of the triangle to the length of the adjacent side. Thus, we have
\(tanθ=\frac{h}{5000}\).
This gives us the equation
\(h=5000tanθ.\)
Step 4. Differentiating this equation with respect to time \(t\), we obtain
\(\frac{dh}{dt}=5000sec^2θ\frac{dθ}{dt}\).
Step 5. We want to find \(\frac{dθ}{dt}\) when \(h=1000ft.\) At this time, we know that \(\frac{dh}{dt}=600ft/sec\). We need to determine \(sec^2θ\). Recall that \(secθ\) is the ratio of the length of the hypotenuse to the length of the adjacent side. We know the length of the adjacent side is \(5000ft\). To determine the length of the hypotenuse, we use the Pythagorean theorem, where the length of one leg is \(5000ft\), the length of the other leg is \(h=1000ft\), and the length of the hypotenuse is c feet as shown in the following figure.
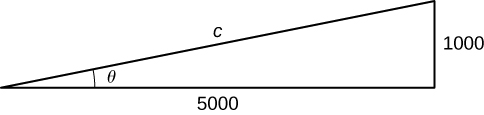
We see that
\(1000^2+5000^2=c^2\)
and we conclude that the hypotenuse is
\(c=1000\sqrt{26}ft.\)
Therefore, when \(h=1000,\) we have
\(sec^2θ=(\frac{1000\sqrt{26}}{5000})^2=\frac{26}{25}.\)
Recall from step 4 that the equation relating \(frac{dθ}{dt}\) to our known values is
\(\frac{dh}{dt}=5000sec^2θ\frac{dθ}{dt}.\)
When \(h=1000ft,\) we know that \(\frac{dh}{dt}=600ft/sec\) and \(sec^2θ=\frac{26}{25}\). Substituting these values into the previous equation, we arrive at the equation
\(600=5000(\frac{26}{25})\frac{dθ}{dt}\).
Therefore, \(\frac{dθ}{dt}=\frac{3}{26}rad/sec.\)
Exercise \(\PageIndex{4}\)
What rate of change is necessary for the elevation angle of the camera if the camera is placed on the ground at a distance of \(4000ft\) from the launch pad and the velocity of the rocket is 500 ft/sec when the rocket is \(2000ft\) off the ground?
- Hint
-
Find \(\frac{dθ}{dt}\) when \(h=2000ft.\) At that time, \(\frac{dh}{dt}=500ft/sec.\)
- Answer
-
\(\frac{1}{10}rad/sec\)
In the next example, we consider water draining from a cone-shaped funnel. We compare the rate at which the level of water in the cone is decreasing with the rate at which the volume of water is decreasing.
Example \(\PageIndex{5}\): Water Draining from a Funnel
Water is draining from the bottom of a cone-shaped funnel at the rate of \(0.03ft^3/sec.\) The height of the funnel is 2 ft and the radius at the top of the funnel is \(1ft\). At what rate is the height of the water in the funnel changing when the height of the water is \(\frac{1}{2}ft\)?
(The volume of the cone is \(1/3 \pi r^2 h\) where \(r\) is the radius and \(h\) is the height.)
Solution: Step 1: Draw a picture introducing the variables.
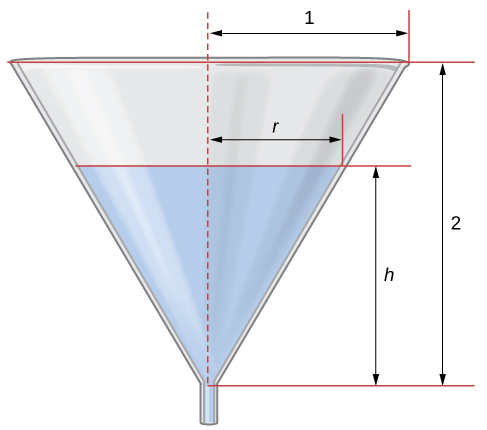
Let \(h\) denotes the height of the water in the funnel, r denotes the radius of the water at its surface, and \(V\) denotes the volume of the water at time \(t\).
Step 2: We need to determine \(\frac{dh}{dt}\) when \(h=\frac{1}{2}ft\). We know that \(\frac{dV}{dt}=−0.03ft/sec.\)
Step 3: The volume of water in the cone is
\(V=\frac{1}{3}πr^2h.\)
From the figure, we see that we have similar triangles. Therefore, the ratio of the sides in the two triangles is the same. Therefore, \(\frac{r}{h}=\frac{1}{2}\) or \(r=\frac{h}{2}.\) Using this fact, the equation for volume can be simplified to
\(V=\frac{1}{3}π(\frac{h}{2})^2h=\frac{π}{12}h^3\).
Step 4: Applying the chain rule while differentiating both sides of this equation with respect to time \(t\), we obtain
\(\frac{dV}{dt}=\frac{π}{4}h^2\frac{dh}{dt}.\)
Step 5: We want to find \(\frac{dh}{dt}\) when \(h=\frac{1}{2}ft\). Since water is leaving at the rate of \(0.03ft^3/sec\), we know that \(\frac{dV}{dt}=−0.03ft^3/sec.\) Therefore,
\(−0.03=\frac{π}{4}(\frac{1}{2})^2\frac{dh}{dt},\)
which implies
\(−0.03=\frac{π}{16}\frac{dh}{dt}.\)
It follows that
\(\frac{dh}{dt}=−\frac{0.48}{π}=−0.153ft/sec.\)
Exercise \(\PageIndex{5}\)
At what rate is the height of the water changing when the height of the water is \(\frac{1}{4}ft\)?
- Hint
-
We need to find \(\frac{dh}{dt}\) when \(h=\frac{1}{4}.\)
- Answer
-
\(−0.61ft/sec\)
Example \(\PageIndex{6}\):
Oil spilled from a tanker spreads in a circle whose area increases at a constant rate of \( 6 \,km^2/h\). How fast the circumference increasing when the radius is \(3\, km\).
Exercise \(\PageIndex{6}\)
Oil spilled from a tanker spreads in a circle whose circumference increases at a constant rate of \( 6 \,km/h\). How fast the area increasing when the radius is \(3\, km\).
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Example \(\PageIndex{7}\):
The altitude(height) of a right triangle is increasing a ta rate of \(2 \,cm/min\) while the area of a triangle is increasing at a rate of \( 4\,cm^2/min \). At what rate is the base of the triangle changing when the altitude is \(10 \,cm\) and the area is \( 100\,cm^2.\)
Exercise \(\PageIndex{7}\)
The altitude(height) of a right triangle is increasing a ta rate of \(2 \,cm/min\) while the area of a triangle is increasing at a rate of \( 4\,cm^2/min \). At what rate is the base of the triangle changing when the altitude is \(5 \,cm\) and the area is \( 25\,cm^2.\)
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Example \(\PageIndex{8}\):
When air expands the pressure \(P\) and the volume \(V\) of the air satisfy the relationship \(PV^{7/5}=k\) where \(k\) is a constant. At a certain instant, the pressure is \(10\, lb/in^2\), and the volume is \(10^4\, in^3\). If the volume is decreasing at the rate of \(5 \, in^3/s\) at this instant, what is the rate of change of the pressure?
Key Concepts
- To solve a related rates problem, first draw a picture that illustrates the relationship between the two or more related quantities that are changing with respect to time.
- In terms of the quantities, state the information given and the rate to be found.
- Find an equation relating the quantities.
- Use differentiation, applying the chain rule as necessary, to find an equation that relates the rates.
- Be sure not to substitute a variable quantity for one of the variables until after finding an equation relating the rates.
Glossary
- related rates
- are rates of change associated with two or more related quantities that are changing over time
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

