3E: Chapter Exercises
- Page ID
- 10940
This page is a draft and is under active development.
Chapter Review Exercises
Exercise \(\PageIndex{1}\)
True or False? Justify your answer with a proof or a counterexample. Assume that \(f(x)\) is continuous and differentiable unless stated otherwise.
1) If \(f(−1)=−6\) and \(f(1)=2\), then there exists at least one point \(x∈[−1,1]\) such that \(f′(x)=4.\)
- Answer
-
True, by Mean Value Theorem
2) If \(f′(c)=0,\) there is a maximum or minimum at \(x=c.\)
3) There is a function such that \(f(x)<0,f′(x)>0,\) and \(f''(x)<0.\) (A graphical “proof” is acceptable for this answer.)
- Answer
-
True
4) There is a function such that there is both an inflection point and a critical point for some value \(x=a.\)
Exercise \(\PageIndex{2}\)
Given the graph of \(f′\), determine where \(f\) is increasing or decreasing.
- Answer
-
Increasing: \((−2,0)∪(4,∞)\), decreasing: \((−∞,−2)∪(0,4)\)
Exercise \(\PageIndex{3}\)
The graph of \(f\) is given below. Draw \(f′\).
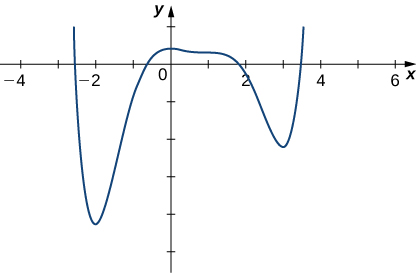
- Answer
-
Under Construction
Exercise \(\PageIndex{4}\)
Find the linear approximation \(L(x)\) to \(y=x^2+tan(πx)\) near \(x=\frac{1}{4}.\)
- Answer
-
\(L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)(x−\frac{1}{4})\)
Exercise \(\PageIndex{5}\)
Find the differential of \(y=x^2−5x−6\) and evaluate for \(x=2\) with \(dx=0.1.\)
- Answer
-
Under Construction
Exercise \(\PageIndex{6}\)
Find the critical points and the local and absolute extrema of the following functions on the given interval.
1) \(f(x)=x+sin^2(x)\) over \([0,π]\)
- Answer
-
Critical point: \(x=\frac{3π}{4},\) absolute minimum: \(x=0,\) absolute maximum: \(x=π\)
2) \(f(x)=3x^4−4x^3−12x^2+6\) over \([−3,3]\)
Exercise \(\PageIndex{7}\)
Determine over which intervals the following functions are increasing, decreasing, concave up, and concave down.
1) \(x(t)=3t^4−8t^3−18t^2\)
- Answer
-
Increasing: \((−1,0)∪(3,∞)\)
Decreasing: \((−∞,−1)∪(0,3)\)
Concave up: \((−∞,\frac{1}{3}(2−\sqrt{13}))∪(\frac{1}{3}(2+\sqrt{13}),∞)\)
Concave down: \((\frac{1}{3}(2−\sqrt{13}),\frac{1}{3}(2+\sqrt{13}))\)
2) \(y=x+sin(πx)\)
3) \(g(x)=x−\sqrt{x}\)
- Answer
-
Increasing: \((\frac{1}{4}∞),\)
Decreasing: \((0,\frac{1}{4})\)
Concave up: \((0,∞)\)
Concave down: nowhere
4) \(f(θ)=\sin(3θ)\)
Exercise \(\PageIndex{8}\)
Evaluate the following \limits.
1) \(\lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x4−1}}\)
- Answer
-
\(3\)
2) \(\lim_{x→∞}cos(\frac{1}{x})\)
3) \(\lim_{x→1}\frac{x−1}{sin(πx)}\)
- Answer
-
\(−\frac{1}{π}\)
4) \(\lim_{x→∞}(3x)^{1/x}\)
Exercise \(\PageIndex{9}\)
Use Newton’s method to find the first two iterations, given the starting point.
1) \(y=x^3+1,x_0=0.5\)
- Answer
-
\(x_1=−1,x_2=−1\)
2) \(\frac{1}{x+1}=\frac{1}{2},x_0=0\)
Exercise \(\PageIndex{10}\)
Find the antiderivatives \(F(x)\) of the following functions.
1) \(g(x)=\sqrt{x}−\frac{1}{x^2}\)
- Answer
-
\(F(x)=\frac{2x^{3/2}}{3}+\frac{1}{x}+C\)
2) \(f(x)=2x+6cosx,F(π)=π^2+2\)
Exercise \(\PageIndex{11}\)
Graph the following functions by hand. Make sure to label the inflection points, critical points, zeros, and asymptotes.
1) \(y=\frac{1}{x(x+1)^2}\)
- Answer
-
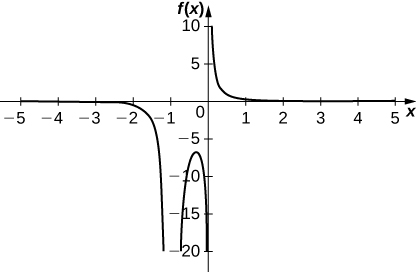
Inflection points: none
Critical points: \(x=−\frac{1}{3}\)
Zeros: none; vertical asymptotes: \(x=−1, x=0\)
Horizontal asymptote: \(y=0\)
2) \(y=x−\sqrt{4−x^2}\)
Exercise \(\PageIndex{12}\)
A car is being compacted into a rectangular solid. The volume is decreasing at a rate of \(2 m^3/sec\). The length and width of the compactor are square, but the height is not the same length as the length and width. If the length and width walls move toward each other at a rate of \(0.25\) m/sec, find the rate at which the height is changing when the length and width are \(2\) m and the height is \(1.5\) m.
- Answer
-
The height is decreasing at a rate of \(0.125\) m/sec
Exercise \(\PageIndex{13}\)
A rocket is launched into space; its kinetic energy is given by \(K(t)=(\frac{1}{2})m(t)v(t)^2\), where \(K\) is the kinetic energy in joules, \(m\) is the mass of the rocket in kilograms, and \(v\) is the velocity of the rocket in meters/second. Assume the velocity is increasing at a rate of \(15 m/sec^2\) and the mass is decreasing at a rate of \(10\) kg/sec because the fuel is being burned. At what rate is the rocket’s kinetic energy changing when the mass is \(2000\) kg and the velocity is \(5000\) m/sec? Give your answer in mega-Joules (MJ), which is equivalent to \(10^6\) J.
- Answer
-
Under Construction
Exercise \(\PageIndex{14}\)
The famous Regiomontanus’ problem for angle maximization was proposed during the \(15\) th century. A painting hangs on a wall with the bottom of the painting a distance \(a\) feet above eye level, and the top \(b\) feet above eye level. What distance x (in feet) from the wall should the viewer stand to maximize the angle subtended by the painting, \(θ\)?
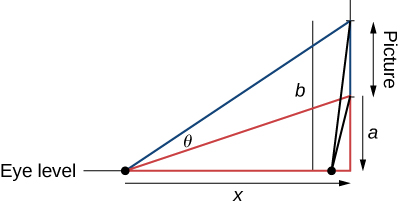
- Answer
-
\(x=\sqrt{ab}\) feet
Exercise \(\PageIndex{15}\)
An airline sells tickets from Tokyo to Detroit for \($1200.\) There are \(500\) seats available and a typical flight books \(350\) seats. For every \($10\) decrease in price, the airline observes an additional five seats sold. What should the fare be to maximize profit? How many passengers would be onboard?
- Answer
-
Under Construction
Exercise \(\PageIndex{16}\)
For the following functions:
a. Find the interval(s) on which \(f(x)\) is increasing
b. Find the interval(s) on which \(f(x)\) is decreasing
c. Find the local (relative) maximum and local (relative) minimum (if any).
1) \(f(x)=x^2 e^{-x}\)
2) \(f(x)=3(x^2-4)^{2/3}\)
3) \(f(x)=x+\frac{1}{x}\)
- Answer
-
Under Construction
Exercise \(\PageIndex{17}\)
For the following functions:
a. Find the interval(s) on which \(g(x)\) is concave up
b. Find the interval(s) on which \(g(x)\) is concave down
c. Find the inflection points (if any)
1) \(g(x)=10x^3+ 3x^5\)
2) \(g(x)=e^{-x^2/2}\)
3) \(g(x)=5x^3+ 2x^5\)
4) \(g(x)=\ln(1+x^2)\)
5) \(g(x)=(3-x^2)^2\)
- Answer
-
Under Construction
Exercise \(\PageIndex{18}\)
Find the horizontal asymptote
\(y=f(x)= x- \sqrt{x^2+2x-6}\)
- Answer
-
Under Construction
Exercise \(\PageIndex{19}\)
\(f(t)=\frac{1}{1-t^2}\)
a. Find vertical and horizontal asymptotes (if any)
b. Find the intervals when \(f(t)\) is concave up and concave down
- Answer
-
Under Construction
Exercise \(\PageIndex{20}\)
\(f(t)=e^{-t^2}\)
a. Find the local maxima and minima for the function \(f(t)\)
b. Find the intervals when \(f(t)\) is increasing and decreasing
c. Find the intervals when \(f(t)\) is concave up and concave down
d. Find the inflection points for \(f(t)\)
- Answer
-
Under Construction
Exercise \(\PageIndex{21}\)
Find all vertical and horizontal asymptotes for the function and justify your work using \limits.
\(f(x)=\frac{x^2-5x+6}{x^2-4x+3}\)
- Answer
-
Under Construction
Exercise \(\PageIndex{22}\)
Using the following information:
\(y=\frac{x}{x^2-1},\qquad y^\prime=-\frac{x^2+1}{\left(x^2-1\right)^2},\mbox{ and }y^{\prime\prime}=\frac{2x\left(x^2+3\right)}{\left(x^2-1\right)^3}\)
a) Identify any asymptotes for the function \(y\) using \limits.
b) Find where the function \(y\) is increasing/decreasing and any relative extrema.
c) Find where the function \(y\) is concave up/down and any points of inflection.
d) Graph the function \(y\)
- Answer
-
Under Construction
Exercise \(\PageIndex{23}\)
Let \(f(x) = x^{5/4}-x^{1/4}\)
Determine the intervals on which \(f\) is increasing and decreasing and find any local extrema.
- Answer
-
Under Construction
Exercise \(\PageIndex{24}\)
Let \(g(x) = \ln (x^2+1)\)
Determine the intervals of concavity of \(g(x)\) and locate any inflection points.
- Answer
-
Under Construction
Exercise \(\PageIndex{25}\)
Determine the intervals of concavity of \(g(x)\) and locate any inflection points:
1) \(g(x) = (\ln x)^2\)
2) \(g(x) = x-2 \tan^{-1}(x)\)
- Answer
-
Under Construction
Exercise \(\PageIndex{26}\)
Find interval(s) on which the function is concave up and the interval(s) on which the function is concave down, and inflection point(s):
\(y=f(x)= x-2tan^{-1}(x)\)
- Answer
-
Under Construction
Exercise \(\PageIndex{27}\)
Let \(f(x) = x^2e^{-16x^2}\)
Determine the intervals on which \(f\) is increasing and decreasing and find any local extrema.
- Answer
-
Under Construction
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

