4.3E: Exercises
- Page ID
- 13732
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
1. A fundamental calculus technique is to use ________ to refine approximations to get an exact answer.
2. What is the upper bound in the summation \(\sum_{i=7}^{14} (48i-201)\)?
3. This section approximates definite integrals using what geometric shape?
4. T/F: A sum using the Right Hand Rule is an example of a Riemann Sum.
- Answer
-
Under Construction
Exercise \(\PageIndex{2}\)
Write out each term of the summation and compute the sum.
1. \(\sum_{i=2}^4 i^2\)
2. \(\sum_{i=-1}^3 (4i-2)\)
3. \(\sum_{i=-2}^2 \sin (\pi i/2)\)
4. \(\sum_{i=1}^5 \frac{1}{i}\)
5. \(\sum_{i=1}^6 (-1)^i i\)
6. \(\sum_{i=1}^4 \left ( \frac{1}{i}-\frac{1}{i+1}\right )\)
7. \(\sum_{i=0}^5 (-1)^i \cos (\pi i)\)
- Answer
-
Under Construction
Exercise \(\PageIndex{3}\)
Write each sum in summation notation.
1. \(3+6+9+12+15\)
2. \(-1+0+3+8+15+24+35+48+63\)
3. \(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\frac{4}{5}\)
4. \(1-e+e^2-e^3+e^4\)
- Answer
-
Under Construction
Exercise \(\PageIndex{4}\)
Evaluate the summation using Theorem 37.
1. \(\sum_{i=1}^25 i\)
2. \(\sum_{i=1}^10 (3i^2-2i)\)
3. \(\sum_{i=1}^15 (2i^3-10)\)
4. \(\sum_{i=1}^10 (-4i^3+10i^2-7i+11)\)
5. \(\sum_{i=1}^10 (i^3-3t^2+2i+7)\)
6. \(1+2+3+... + 99+100\)
7. \(1+4+9+...+361+400\)
- Answer
-
Under Construction
Exercise \(\PageIndex{5}\)
Theorem 37 states:
\(\sum_{i=1}^n a_i = \sum+{i=1}^k a_i+\sum_{i=k+1}^n a_i\), so
\(\sum_{i=k+1}^n a_i = \sum_{i=1}^n a_i -\sum_{i=1}^k a_i \).
Use this fact, along with other parts of Theorem 37, to evaluate the summations given
1. \(\sum_{i=11}^20 i\)
2. \(\sum_{i=16}^25 i^3\)
3. \(\sum_{i=7}^12 4\)
4. \(\sum_{i=5}^10 4i^3\)
- Answer
-
Under Construction
Exercise \(\PageIndex{6}\)
A definite integral \(\int_a^b f(x)\,dx \) is given.
(a) Graph \(f(x)\) on [a,b].
(b) Add to the sketch rectangles using the provided rule.
(c) Approximate \(\int_a^b f(x)\,dx\) by summing the areas of the rectangles.
1. \(\int_{-3}^3 x^2\,dx\), with 6 rectangles using the Left Hand Rule.
2. \(\int_{0}^2 (5-x^2)\,dx\), with 4 rectangles using the Midpoint Rule.
3. \(\int_0^{\pi}\sin x\,dx\), with 6 rectangles using the Right Hand Rule.
4. \(\int_0^3 2^x\,dx\), with 5 rectangles using the Left Hand Rule.
5. \(\int_1^2 \ln x\,dx\), with 3 rectangles using the Midpoint Rule.
6. \(\int_1^9 \frac{1}{x} \,dx\), with 4 rectangles using the Right Hand Rule.
- Answer
-
Under Construction
Exercise \(\PageIndex{7}\)
A definite integral \(\int_a^b f(x)\,dx\) is given.
(a) Find a formula to approximate \(\int_a^b f(x)\,dx\) using \(n\) subintervals and the provided rule.
(b) Evaluate the formula using \(n=10,\,100\text{ and }1000.\)
(c) Find the limit of the formula, as \(n\to \infty\), to find the exact value of \(\int_a^b f(x)\,dx\).
1. \(\int_0^1 x^3\,dx\), using the Right Hand Rule.
2. \(\int_{-1}^1 3x^2\,dx\), using the Left Hand Rule.
3. \(\int_{-1}^3 (3x-1)\,dx\), using the Midpoint Rule.
4. \(\int_1^4 (2x^2-3)\,dx\), using the Left Hand Rule.
5. \(\int_{-10}^{10}(5-x)\,dx\), using the Right Hand Rule.
6. \(\int_0^1 (x^3-x^2)\,dx\), using the Right Hand Rule.
- Answer
-
Under Construction
Exercise \(\PageIndex{8}\)
Find an antiderivative of the given function.
1. \(f(x) = 5\sec^2 x\)
2. \(f(x) = \frac{7}{x}\)
3. \(g(t) = 4t^5-5t^3+8\)
4. \(g(t) =5\cdot 8^t\)
5. \(g(t) =\cos t +\sin t\)
6. \(f(x) =\frac{1}{\sqrt{x}}\)
- Answer
-
Under Construction
Exercise \(\PageIndex{9}\)
State whether the given sums are equal or unequal.
1. \(\displaystyle \sum_{i=1}^{10}i\) and \(\displaystyle \sum_{k=1}^{10}k\)
- Answer
-
They are equal; both represent the sum of the first 10 whole numbers
2. \(\displaystyle \sum_{i=1}^{10}i\) and \(\displaystyle \sum_{i=6}^{15}(i−5)\)
- Answer
-
They are equal; both represent the sum of the first 10 whole numbers
3. \(\displaystyle \sum_{i=1}^{10}i(i−1)\) and \(\displaystyle \sum_{j=0}^9(j+1)j\)
- Answer
-
They are equal by substituting \(\displaystyle j=i−1.\)
4. \(\displaystyle \sum_{i=1}^{10}i(i−1)\) and \(\displaystyle \sum_{k=1}^{10}(k^2−k)\)
- Answer
-
They are equal; the first sum factors the terms of the second.
Exercise \(\PageIndex{10}\)
In the following exercises, use the rules for sums of powers of integers to compute the sums.
1. \(\displaystyle \sum_{i=5}^{10}i\)
2. \(\displaystyle \sum_{i=5}^{10}i^2\)
- Answer
-
\(\displaystyle 385−30=355\)
Exercise \(\PageIndex{11}\)
Suppose that \(\displaystyle \sum_{i=1}^{100}a_i=15\) and \(\displaystyle \sum_{i=1}^{100}b_i=−12.\)
In the following exercises, compute the sums.
1. \(\displaystyle \sum_{i=1}^{100}(a_i+b_i)\)
2. \(\displaystyle \sum_{i=1}^{100}(a_i−b_i)\)
- Answer
-
\(\displaystyle 15−(−12)=27\)
3. \(\displaystyle \sum_{i=1}^{100}(3a_i−4b_i)\)
4. \(\displaystyle \sum_{i=1}^{100}(5a_i+4b_i)\)
- Answer
-
\(\displaystyle 5(15)+4(−12)=27\)
Exercise \(\PageIndex{12}\)
In the following exercises, use summation properties and formulas to rewrite and evaluate the sums.
1. \(\displaystyle \sum_{k=1}^{20}100(k^2−5k+1)\)
2. \(\displaystyle \sum_{j=1}^{50}(j^2−2j)\)
- Answer
-
\(\displaystyle \sum_{j=1}^{50}j%2−2\sum_{j=1}^{50}j=\frac{(50)(51)(101)}{6}−\frac{2(50)(51)}{2}=40, 375\)
3. \(\displaystyle \sum_{j=11}^{20}(j^2−10j)\)
4. \(\displaystyle \sum_{k=1}^{25}[(2k)^2−100k]\)
- Answer
-
\(\displaystyle 4\sum_{k=1}^{25}k^2−100\sum_{k=1}^{25}k=\frac{4(25)(26)(51)}{9}−50(25)(26)=−10, 400\)
Exercise \(\PageIndex{13}\)
Let \(\displaystyle L_n\) denote the left-endpoint sum using n subintervals and let \(\displaystyle R_n\) denote the corresponding right-endpoint sum.
In the following exercises, compute the indicated left and right sums for the given functions on the indicated interval.
1. \(\displaystyle L_4\) for \(\displaystyle f(x)=\frac{1}{x−1}\) on \(\displaystyle [2,3]\)
2. \(\displaystyle R_4\) for \(\displaystyle g(x)=cos(πx)\) on \(\displaystyle [0,1]\)
- Answer
-
\(\displaystyle R_4=0.25\)
3. \(\displaystyle L_6\) for \(\displaystyle f(x)=\frac{1}{x(x−1)}\) on \(\displaystyle [2,5]\)
4. \(\displaystyle R_6\) for \(\displaystyle f(x)=\frac{1}{x(x−1)}\) on \(\displaystyle [2,5]\)
- Answer
-
\(\displaystyle R_6=0.372\)
5. \(\displaystyle R_4\) for \(\displaystyle \frac{1}{x^2+1}\) on \(\displaystyle [−2,2]\)
6. \(\displaystyle L_4\) for \(\displaystyle \frac{1}{x^2+1}\) on \(\displaystyle [−2,2]\)
- Answer
-
\(\displaystyle L_4=2.20\)
7. \(\displaystyle R_4\) for \(\displaystyle x^2−2x+1\) on \(\displaystyle [0,2]\)
8. \(\displaystyle L_8\) for \(\displaystyle x^2−2x+1\) on \(\displaystyle [0,2]\)
- Answer
-
\(\displaystyle L_8=0.6875\)
Exercise \(\PageIndex{14}\)
1. Compute the left and right Riemann sums— \(\displaystyle L_4\) and \(\displaystyle R_4\), respectively—for \(\displaystyle f(x)=(2−|x|)\) on \(\displaystyle [−2,2].\) Compute their average value and compare it with the area under the graph of f.
2. Compute the left and right Riemann sums— \(\displaystyle L_6\) and \(\displaystyle R_6\), respectively—for \(\displaystyle f(x)=(3−|3−x|)\) on \(\displaystyle [0,6].\) Compute their average value and compare it with the area under the graph of f.
- Answer
-
\(\displaystyle L_6=9.000=R_6\). The graph of f is a triangle with area 9.
3. Compute the left and right Riemann sums— \(\displaystyle L_4\) and \(\displaystyle R_4\), respectively—for \(\displaystyle f(x)=\sqrt{4−x^2}\) on \(\displaystyle [−2,2]\) and compare their values.
4. Compute the left and right Riemann sums— \(\displaystyle L_6\) and \(\displaystyle R_6\), respectively—for \(\displaystyle f(x)=\sqrt{9−(x−3)^2}\) on \(\displaystyle [0,6]\) and compare their values.
- Answer
-
\(\displaystyle L_6=13.12899=R_6\). They are equal.
Exercise \(\PageIndex{15}\)
Express the following endpoint sums in sigma notation but do not evaluate them.
1. \(\displaystyle L_{30}\) for \(\displaystyle f(x)=x^2\) on \(\displaystyle [1,2]\)
2. \(\displaystyle L_{10}\) for \(\displaystyle f(x)=\sqrt{4−x^2}\) on \(\displaystyle [−2,2]\)
- Answer
-
\(\displaystyle L_{10}=\frac{4}{10}\sum_{i=1}^{10}\sqrt{4−(−2+4\frac{(i−1)}{10})}\)
3. \(\displaystyle R_{20}\) for \(\displaystyle f(x)=sinx\) on \(\displaystyle [0,π]\)
4. \(\displaystyle R_{100}\) for \(\displaystyle lnx\) on \(\displaystyle [1,e]\)
- Answer
-
\(\displaystyle R_{100}=\frac{e−1}{100}\sum_{i=1}^{100}ln(1+(e−1)\frac{i}{100})\)
Exercise \(\PageIndex{16}\)
In the following exercises, graph the function then use a calculator or a computer program to evaluate the following left and right endpoint sums. Is the area under the curve between the left and right endpoint sums?
1. \(\displaystyle L_{100}\) and \(\displaystyle R_{100}\) for \(\displaystyle y=x^2−3x+1\) on the interval \(\displaystyle [−1,1]\)
2. \(\displaystyle L_{100}\) and \(\displaystyle R_{100}\) for \(\displaystyle y=x^2\) on the interval \(\displaystyle [0,1]\)
- Answer
-
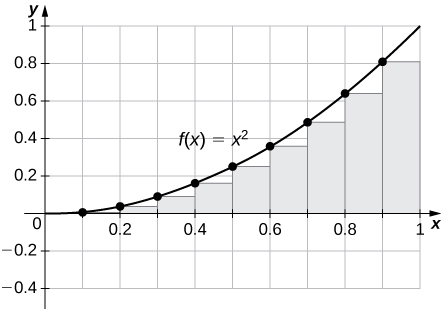
\(\displaystyle R_{100}=0.33835,L_{100}=0.32835.\) The plot shows that the left Riemann sum is an underestimate because the function is increasing. Similarly, the right Riemann sum is an overestimate. The area lies between the left and right Riemann sums. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
3. \(\displaystyle L_{50}\) and \(\displaystyle R_{50}\) for \(\displaystyle y=\frac{x+1}{x^2−1}\) on the interval \(\displaystyle [2,4]\)
4. \(\displaystyle L_{100}\) and \(\displaystyle R_{100}\) for \(\displaystyle y=x^3\) on the interval \(\displaystyle [−1,1]\)
- Answer
-
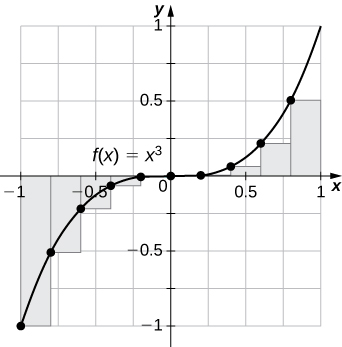
\(\displaystyle L_{100}=−0.02,R_{100}=0.02\). The left endpoint sum is an underestimate because the function is increasing. Similarly, a right endpoint approximation is an overestimate. The area lies between the left and right endpoint estimates.
5. \(\displaystyle L_{50}\) and \(\displaystyle R_{50}\) for \(\displaystyle y=tan(x)\) on the interval \(\displaystyle [0,\frac{π}{4}]\)
6. \(\displaystyle L_{100}\) and \(\displaystyle R_{100}\) for \(\displaystyle y=e^{2x}\) on the interval \(\displaystyle [−1,1]\)
Answer
-
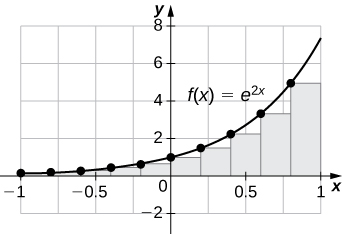
\(\displaystyle L_{100}=3.555,R_{100}=3.670\). The plot shows that the left Riemann sum is an underestimate because the function is increasing. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
Exercise \(\PageIndex{17}\)
1. Let \(\displaystyle t_j\) denote the time that it took Tejay van Garteren to ride the jth stage of the Tour de France in 2014. If there were a total of 21 stages, interpret \(\displaystyle \sum_{j=1}^{21}t_j\).
2. Let \(\displaystyle r_j\) denote the total rainfall in Portland on the jth day of the year in 2009. Interpret \(\displaystyle \sum_{j=1}^{31}r_j\).
- Answer
-
The sum represents the cumulative rainfall in January 2009.
3. Let \(\displaystyle d_j\) denote the hours of daylight and \(\displaystyle δ_j\) denote the increase in the hours of daylight from day \(\displaystyle j−1\) to day j in Fargo, North Dakota, on thejth day of the year. Interpret \(\displaystyle d1+\sum_{j=2}^{365}δ_j\).
4. To help get in shape, Joe gets a new pair of running shoes. If Joe runs 1 mi each day in week 1 and adds \(\displaystyle \frac{1}{10}\) mi to his daily routine each week, what is the total mileage on Joe’s shoes after 25 weeks?
- Answer
-
The total mileage is \(\displaystyle 7×\sum_{i=1}^{25}(1+\frac{(i−1)}{10})=7×25+\frac{7}{10}×12×25=385mi\).
Exercise \(\PageIndex{18}\)
1. The following table gives approximate values of the average annual atmospheric rate of increase in carbon dioxide (CO2) each decade since 1960, in parts per million (ppm). Estimate the total increase in atmospheric CO2 between 1964 and 2013.
| Decade | Ppm/y |
|---|---|
| 1964-1973 | 1.07 |
| 1976-1983 | 1.34 |
| 1984-1993 | 1.40 |
| 1994-2003 | 1.87 |
| 2004-2013 | 2.07 |
Average Annual Atmospheric CO2 Increase, 1964–2013 Source: http://www.esrl.noaa.gov/gmd/ccgg/trends/.
2. The following table gives the approximate increase in sea level in inches over 20 years starting in the given year. Estimate the net change in mean sea level from 1870 to 2010.
| Starting Year | 20- Year Change |
|---|---|
| 1870 | 0.3 |
| 1890 | 1.5 |
| 1910 | 0.2 |
| 1930 | 2.8 |
| 1950 | 0.7 |
| 1970 | 1.1 |
| 1990 | 1.5 |
Approximate 20-Year Sea Level Increases, 1870–1990
Source: http://link.springer.com/article/10....712-011-9119-1
- Answer
-
Add the numbers to get 8.1-in. net increase.
3. The following table gives the approximate increase in dollars in the average price of a gallon of gas per decade since 1950. If the average price of a gallon of gas in 2010 was $2.60, what was the average price of a gallon of gas in 1950?
| Starting Year | 10- Year Change |
|---|---|
| 1950 | 0.03 |
| 1960 | 0.05 |
| 1970 | 0.86 |
| 1980 | −0.03 |
| 1990 | 0.29 |
| 2000 | 1.12 |
Approximate 10-Year Gas Price Increases, 1950–2000
Source: epb.lbl.gov/homepages/Rick_Di...011-trends.pdf.
4. The following table gives the percent growth of the U.S. population beginning in July of the year indicated. If the U.S. population was 281,421,906 in July 2000, estimate the U.S. population in July 2010.
| Year | % Change/Year |
|---|---|
| 2000 | 1.12 |
| 2001 | 0.99 |
| 2002 | 0.93 |
| 2003 | 0.86 |
| 2004 | 0.93 |
| 2005 | 0.93 |
| 2006 | 0.97 |
| 2007 | 0.96 |
| 2008 | 0.95 |
| 2009 | 0.88 |
Annual Percentage Growth of U.S. Population, 2000–2009
Source: www.census.gov/popest/data.
(Hint: To obtain the population in July 2001, multiply the population in July 2000 by 1.0112 to get 284,573,831.)
- Answer
-
309,389,957
Exercise \(\PageIndex{19}\)
In the following exercises, estimate the areas under the curves by computing the left Riemann sums, \(\displaystyle L_8.\)
1.
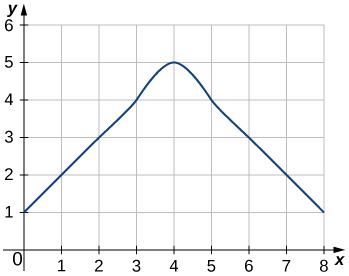
2.
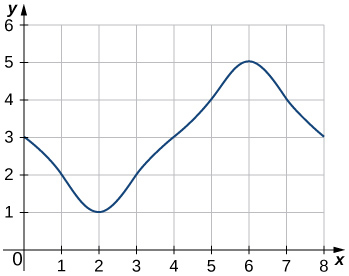
- Answer
-
\(\displaystyle L_8=3+2+1+2+3+4+5+4=24\)
3.
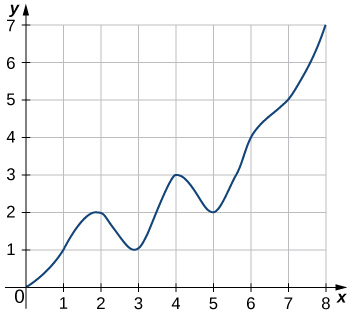
4.
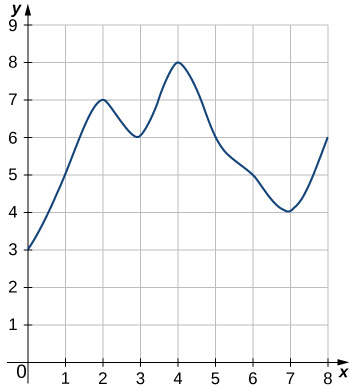
- Answer
-
\(\displaystyle L_8=3+5+7+6+8+6+5+4=44\)
Exercise \(\PageIndex{20}\)
Use a computer algebra system to compute the Riemann sum:
1. \(\displaystyle L_N\), for \(\displaystyle N=10,30,50\) for \(\displaystyle f(x)=\sqrt{1−x^2}\) on \(\displaystyle [−1,1].\)
2. \(\displaystyle L_N\), for \(\displaystyle N=10,30,50\) for \(\displaystyle f(x)=\frac{1}{\sqrt{1+x^2}}\) on \(\displaystyle [−1,1].\)
- Answer
-
\(\displaystyle L_{10}≈1.7604,L_{30}≈1.7625,L_{50}≈1.76265\)
3. \(\displaystyle L_N\), for \(\displaystyle N=10,30,50\) for \(\displaystyle f(x)=sin^2x\) on \(\displaystyle [0,2π]\). Compare these estimates with π.
Exercise \(\PageIndex{21}\)
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums \(\displaystyle R_N\) and \(\displaystyle L_N\) for \(\displaystyle N=1,10,100\).
How do these estimates compare with the exact answers, which you can find via geometry?
1. \(\displaystyle y=cos(πx)\) on the interval \(\displaystyle [0,1]\)
- Answer
-
\(\displaystyle R_1=−1,L_1=1,R_{10}=−0.1,L_{10}=0.1,L_{100}=0.01,\) and \(\displaystyle R_{100}=−0.1.\) By symmetry of the graph, the exact area is zero.
2. \(\displaystyle y=3x+2\) on the interval \(\displaystyle [3,5]\)
Exercise \(\PageIndex{22}\)
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums \(\displaystyle R_N\) and \(\displaystyle L_N\) for \(\displaystyle N=1,10,100.\)
1. \(\displaystyle y=x^4−5x^2+4\) on the interval \(\displaystyle [−2,2]\), which has an exact area of \(\displaystyle \frac{32}{15}\)
- Answer
-
\(\displaystyle R_1=0,L_1=0,R_{10}=2.4499,L_{10}=2.4499,R_{100}=2.1365,L_{100}=2.1365\)
2. \(\displaystyle y=lnx\) on the interval \(\displaystyle [1,2]\), which has an exact area of \(\displaystyle 2ln(2)−1\
Exercise \(\PageIndex{23}\)
1. Explain why, if \(\displaystyle f(a)≥0\) and f is increasing on \(\displaystyle [a,b]\), that the left endpoint estimate is a lower bound for the area below the graph of \(\displaystyle f\) on \(\displaystyle [a,b].\)
- Answer
-
If \(\displaystyle [c,d]\)is a subinterval of \(\displaystyle [a,b]\) under one of the left-endpoint sum rectangles, then the area of the rectangle contributing to the left-endpoint estimate is \(\displaystyle f(c)(d−c)\).
But, \(\displaystyle f(c)≤f(x)\) for \(\displaystyle c≤x≤d\), so the area under the graph of \(\displaystyle f\) between \(\displaystyle c\) and \(\displaystyle d\) is \(\displaystyle f(c)(d−c)\) plus the area below the graph of f but above the horizontal line segment at height \(\displaystyle f(c)\), which is positive.
As this is true for each left-endpoint sum interval, it follows that the left Riemann sum is less than or equal to the area below the graph of \(\displaystyle f\) on \(\displaystyle [a,b].\)
2. Explain why, if \(\displaystyle f(b)≥0\) and f is decreasing on \(\displaystyle [a,b],\) that the left endpoint estimate is an upper bound for the area below the graph of \(\displaystyle f\) on \(\displaystyle [a,b].\)
3. Show that, in general, \(\displaystyle R_N−L_N=(b−a)×\frac{f(b)−f(a)}{N}.\)
- Answer
-
\(\displaystyle L_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i−1}{N})=\frac{b−a}{N}\sum_{i=0}^{N−1}f(a+(b−a)\frac{i}{N})\) and \(\displaystyle R_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i}{N})\).
The left sum has a term corresponding to \(\displaystyle i=0\) and the right sum has a term corresponding to \(\displaystyle i=N\).
In \(\displaystyle R_N−L_N\), any term corresponding to \(\displaystyle i=1,2,…,N−1\) occurs once with a plus sign and once with a minus sign, so each such term cancels and one is left with \(\displaystyle R_N−L_N=\frac{b−a}{N}(f(a+(b−a))\frac{N}{N})−(f(a)+(b−a)\frac{0}{N})=\frac{b−a}{N}(f(b)−f(a)).\)
4. Explain why, if f is increasing on [ \(\displaystyle a,b\)], the error between either \(\displaystyle L_N\) or \(\displaystyle R_N\) and the area A below the graph of f is at most \(\displaystyle (b−a)\frac{f(b)−f(a)}{N]|).
Exercise \(\PageIndex{24}\)
For each of the three graphs:
a. Obtain a lower bound \(\displaystyle L(A)\) for the area enclosed by the curve by adding the areas of the squares enclosed completely by the curve.
b. Obtain an upper bound \(\displaystyle U(A)\) for the area by adding to \(\displaystyle L(A)\) the areas \(\displaystyle B(A)\) of the squares enclosed partially by the curve.
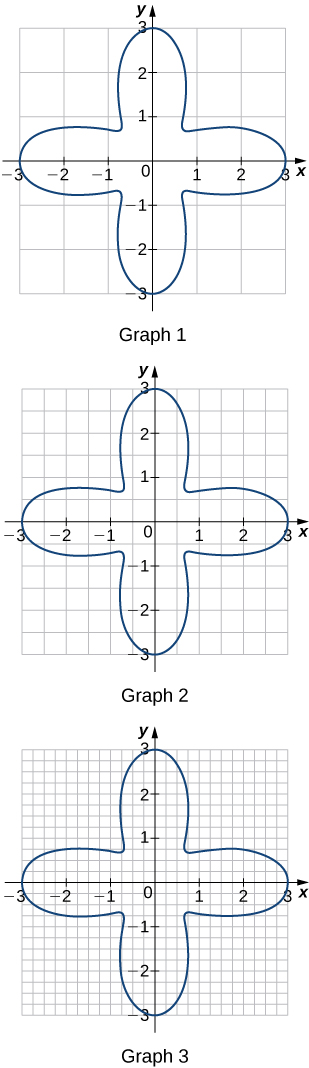
- Answer
-
Graph 1:
a. \(\displaystyle L(A)=0,B(A)=20\)
b. \(U(A)=20.\)
Graph 2:
a. \(\displaystyle L(A)=9\)
b. \(B(A)=11,U(A)=20.\)
Graph 3:
a. \(\displaystyle L(A)=11.0\)
b. \(B(A)=4.5,U(A)=15.5.\)
In the previous exercise, explain why \(\displaystyle L(A)\) gets no smaller while \(\displaystyle U(A)\) gets no larger as the squares are subdivided into four boxes of equal area.
- Answer
-
Under Construction
Exercise \(\PageIndex{25}\)
A unit circle is made up of n wedges equivalent to the inner wedge in the figure. The base of the inner triangle is 1 unit and its height is \(\displaystyle sin(\frac{π}{n}).\) The base of the outer triangle is \(\displaystyle B=cos(\frac{π}{n})+sin(\frac{π}{n})tan(\frac{π}{n})\) and the height is \(\displaystyle H=Bsin(\frac{2π}{n})\). Use this information to argue that the area of a unit circle is equal to π.\)
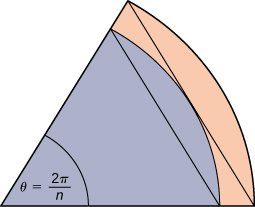
- Answer
-
Let A be the area of the unit circle. The circle encloses n congruent triangles each of area \(\displaystyle \frac{sin(\frac{2π}{n})}{2}\), so \(\displaystyle \frac{n}{2}sin(\frac{2π}{n})≤A.\) Similarly, the circle is contained inside n congruent triangles each of area \(\displaystyle \frac{BH}{2}=\frac{1}{2}(cos(\frac{π}{n})+sin(\frac{π}{n})tan(\frac{π}{n}))sin(\frac{2π}{n})\), so \(\displaystyle A≤\frac{n}{2}sin(\frac{2π}{n})(cos(\frac{π}{n}))+sin(\frac{π}{n})tan(\frac{π}{n})\). As \(\displaystyle n→∞,\frac{n}{2}sin(\frac{2π}{n})=\frac{πsin(\frac{2π}{n})}{(\frac{2π}{n})}→π\), so we conclude \(\displaystyle π≤A\). Also, as \(\displaystyle n→∞,cos(\frac{π}{n})+sin(\frac{π}{n})tan(\frac{π}{n})→1\), so we also have \(\displaystyle A≤π\). By the squeeze theorem for limits, we conclude that \(\displaystyle A=π.\)

