2.2: Equivalence Relations, and Partial order
- Page ID
- 7443
This page is a draft and is under active development.
Definition: Equivalence Relation
A binary relation is an equivalence relation on a nonempty set \(S\) if and only if the relation is reflexive(R), symmetric(S) and transitive(T).
Definition: Partial Order
A binary relation is a partial order if and only if the relation is reflexive(R), antisymmetric(A) and transitive(T).
Example \(\PageIndex{1}\): \(=\)
Let \(S=\mathbb{R}\) and \(R\) be =. Is the relation a) reflexive, b) symmetric, c) antisymmetric, d) transitive, e) an equivalence relation, f) a partial order.
Solution:
Proof:
Proof:
Proof:
Proof:
Proof:
Since is reflexive, symmetric and transitive, it is an equivalence relation.
Proof:
is a partial order, since
is reflexive, antisymmetric and transitive.
Example \(\PageIndex{2}\): Less than or equal to
Let and
be
. Is the relation a) reflexive, b) symmetric, c) antisymmetric, d) transitive, e) an equivalence relation, f) a partial order.
Solution
Proof:
Counterexample:
It is true that , but it is not true that
.
Proof:
We will show that given and
that
.
Proof:
We will show that given and
that
.
5. No, is not an equivalence relation on
since it is not symmetric.
6. Yes, is a partial order on
since it is reflexive, antisymmetric and transitive.
Definition: Equivalence Class
Given an equivalence relation \( R \) over a set \( S, \) for any \(a \in S \) the equivalence class of a is the set \( [a]_R =\{ b \in S \mid a R b \} \), that is
\([a]_R \) is the set of all elements of S that are related to \(a\).
Example \(\PageIndex{3}\): Equivalence relation
Define a relation that two shapes are related iff they are the same color. Is this relation an equivalence relation?
Equivalence classes are:

Example \(\PageIndex{4}\):
Define a relation that two shapes are related iff they are similar. Is this relation an equivalence relation?
Equivalence classes are:

Let \(A\) be a nonempty set. A partition of \(A\) is a set of nonempty pairwise disjoint sets whose union is A.
Note
For every equivalence relation over a nonempty set \(S\), \(S\) has a partition.
Theorem \(\PageIndex{1}\)
If \( \sim \) is an equivalence relation over a non-empty set \(S\). Then the set of all equivalence classes is denoted by \(\{[a]_{\sim}| a \in S\}\) forms a partition of \(S\).
This means
1. Either \([a] \cap [b] = \emptyset\) or \([a]=[b]\), for all \(a,b\in S\).
2. \(S= \cup_{a \in S} [a]\).
- Proof
-
Assume
is an equivalence relation on a nonempty set
.
Let
. If
, then we are done. Otherwise,
Let
be the common element between them.
Then
and
, which means that
and
.
Since
is an equivalence relation and
.
Since
and
(due to transitive property),
.
For the following examples, determine whether or not each of the following binary relations on the given set
is reflexive, symmetric, antisymmetric, or transitive. If a relation has a certain property, prove this is so; otherwise, provide a counterexample to show that it does not. If
is an equivalence relation, describe the equivalence classes of
.
Example \(\PageIndex{5}\):
Let \(S = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\). Define a relation \(R\) on \(A = S \times S \) by \((a, b) R (c, d)\) if and only if \(10a + b \leq 10c + d.\)
Let . Define a relation
on
by
if and only if
.
Solution
Proof:
Counter Example:
Since ,
is not symmetric on
.◻
Proof:
Thus is antisymmetric on
.◻
5. is transitive on .
Proof:
6. is not an equivalence relation since it is not reflexive, symmetric, and transitive.
Example \(\PageIndex{6}\):
Let . Define a relation
on
, by
if and only if
Solution
Proof:
Clearly since
and a negative integer multiplied by a negative integer is a positive integer in
.
Since ,
is reflexive on
.◻
2. is symmetric on
.
Proof:
Counter Example:
Since ,
is not antisymmetric on
.◻
Proof:
There are two cases to be examined:
Since in both possible cases
is transitive on
.◻
5. Since is reflexive, symmetric and transitive, it is an equivalence relation. Equivalence classes are
and
.
Note this is a partition since or
. So we have all the intersections are empty.
Further, we have . Note that
is excluded from
.
Hasse Diagram
Consider the set \( S=\{1,2,3,4,5\}\). Then the relation \(\leq\) is a partial order on \(S\). Check!
Partial orders are often pictured using the Hasse diagram, named after mathematician Helmut Hasse (1898-1979).
Definition: Hasse Diagram
Let S be a nonempty set and let \(R\) be a partial order relation on \(S\). Then Hasse diagram construction is as follows:
- there is a vertex (denoted by dots) associated with every element of \(S\).
- if \( a R b\) , then the vertex \(b\) is positioned higher than vertex \(a\).
- if \( a R b\) and there is no \(c\) such that \(a R c\) and \(c R b\), then a line is drawn from a to b.
This diagram is called the Hasse diagram.
Hasse diagram for \( S=\{1,2,3,4,5\}\) with the relation \(\leq\).
Solution
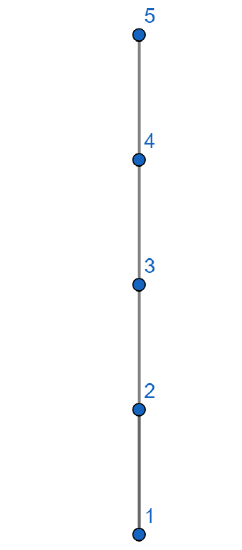
Show that \( \mathbb{Z}_+ \) with the relation \( | \) is a partial order. Draw a Hasse diagram for \( S=\{1,2,3,4,5,6\}\) with the relation \( | \).
Solution