5.2E: Excercises

Exercise \(\PageIndex{1}\)

1) If \(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) and \(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), find the power series of \(\frac{1}{2}\big(f(x)+g(x)\big)\) and of \(\frac{1}{2}\big(f(x)−g(x)\big)\).

Answer:

\(\displaystyle \frac{1}{2}\big(f(x)+g(x)\big)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) and \(\displaystyle \frac{1}{2}\big(f(x)−g(x)\big)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\).

2) If \(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) and \(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), find the power series of \(C(x)+S(x)\) and of \(C(x)−S(x)\).

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{2}\)

In exercises 3 - 6, use partial fractions to find the power series of each function.

3) \(\dfrac{4}{(x−3)(x+1)}\)

Answer:

\(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞\left(\frac{x}{3}\right)^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞\left((−1)^{n+1}−\frac{1}{3n+1}\right)x^n\)

4) \(\dfrac{3}{(x+2)(x−1)}\)

5) \(\dfrac{5}{(x^2+4)(x^2−1)}\)

Answer:

\(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+\left(\frac{x}{2}\right)^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n\left(\frac{x}{2}\right)^n=\sum_{n=0}^∞\left((−1)+(−1)^{n+1}\frac{1}{2^{n+2}}\right)x^{2n}\)

6) \(\dfrac{30}{(x^2+1)(x^2−9)}\)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{3}\)

In exercises 7 - 10, express each series as a rational function.

7) \(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

Answer:

\(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\cdot \frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

8) \(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

9) \(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

Answer:

\(\displaystyle \frac{1}{x−3}\cdot \frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

10) \(\displaystyle \sum_{n=1}^∞\left(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}}\right)\)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{4}\)

Exercises 11 - 16 explore applications of annuities.

11) Calculate the present values \(P\) of an annuity in which $10,000 is to be paid out annually for a period of 20 years, assuming interest rates of \(r=0.03,\, r=0.05\), and \(r=0.07\).

Answer:

\(P=P_1+⋯+P_{20}\) where \(P_k=10,000\dfrac{1}{(1+r)^k}\). Then \(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). When \(r=0.03, \,P≈10,000×14.8775=148,775.\) When \(r=0.05, \,P≈10,000×12.4622=124,622.\) When \(r=0.07, \, P≈105,940\).

12) Calculate the present values \(P\) of annuities in which $9,000 is to be paid out annually perpetually, assuming interest rates of \(r=0.03,\, r=0.05\) and \(r=0.07\).

13) Calculate the annual payouts \(C\) to be given for 20 years on annuities having present value $100,000 assuming respective interest rates of \(r=0.03,\, r=0.05,\) and \(r=0.07.\)

Answer:

In general, \(P=\dfrac{C(1−(1+r)^{−N})}{r}\) for \(N\) years of payouts, or \(C=\dfrac{Pr}{1−(1+r)^{−N}}\). For \(N=20\) and \(P=100,000\), one has \(C=6721.57\) when \(r=0.03; \, C=8024.26\) when \(r=0.05\); and \(C≈9439.29\) when \(r=0.07\).

14) Calculate the annual payouts \(C\) to be given perpetually on annuities having present value $100,000 assuming respective interest rates of \(r=0.03, \,r=0.05,\) and \(r=0.07\).

15) Suppose that an annuity has a present value \(P=1\) million dollars. What interest rate \(r\) would allow for perpetual annual payouts of $50,000?

Answer:

In general, \(P=\dfrac{C}{r}.\) Thus, \(r=\dfrac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

16) Suppose that an annuity has a present value \(P=10\) million dollars. What interest rate \(r\) would allow for perpetual annual payouts of $100,000?

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{5}\)

In exercises 17 - 20, express the sum of each power series in terms of geometric series, and then express the sum as a rational function.

17) \(x+x^2−x^3+x^4+x^5−x^6+⋯\) (Hint: Group powers \(x^{3k}, \, x^{3k−1},\) and \(x^{3k−2}\).)

Answer:

\((x+x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x+x^2−x^3}{1−x^3}\)

18) \(x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (Hint: Group powers \(x^{4k}, \, x^{4k−1},\) etc.)

19) \(x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (Hint: Group powers \(x^{3k}, \, x^{3k−1}\), and \(x^{3k−2}\).)

Answer:

\((x−x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x−x^2−x^3}{1−x^3}\)

20) \(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (Hint: Group powers \(\left(\dfrac{x}{2}\right)^{3k}, \, \left(\dfrac{x}{2}\right)^{3k−1},\) and \(\left(\dfrac{x}{2}\right)^{3k−2}\).)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{6}\)

In exercises 21 - 24, find the power series of \(f(x)g(x)\) given \(f\) and \(g\) as defined.

21) \(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

Answer:

\(a_n=2, \, b_n=n\) so \(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) and \(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

22) \(\displaystyle f(x)=\sum_{n=1}^∞x^n,\; g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Express the coefficients of \(f(x)g(x)\) in terms of \(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

23) \(\displaystyle f(x)=g(x)=\sum_{n=1}^∞\left(\frac{x}{2}\right)^n\)

Answer:

\(a_n=b_n=2^{−n}\) so \(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) and \(\displaystyle f(x)g(x)=\sum_{n=1}^∞n\left(\frac{x}{2}\right)^n\)

24) \(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{7}\)

In exercises 25 - 26, differentiate the given series expansion of \(f\) term-by-term to obtain the corresponding series expansion for the derivative of \(f.\)

25) \(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

Answer:

The derivative of \(f\) is \(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

26) \(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{8}\)

In exercises 27 - 28, integrate the given series expansion of \(f\) term-by-term from zero to \(x\) to obtain the corresponding series expansion for the indefinite integral of \(f\).

27) \(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

Answer:

The indefinite integral of \(f\) is \(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

28) \(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{9}\)

In exercises 29 - 32, evaluate each infinite series by identifying it as the value of a derivative or integral of geometric series.

29) Evaluate \(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) as \(f′\left(\frac{1}{2}\right)\) where \(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Answer:

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}\Big|_{x=1/2}=\frac{1}{(1−x)^2}\Big|_{x=1/2}=4\) so \(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

30) Evaluate \(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) as \(f′\left(\frac{1}{3}\right)\) where \(\displaystyle f(x)=\sum_{n=0}^∞x^{6n}\).

31) Evaluate \(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) as \(f''\left(\frac{1}{2}\right)\) where \(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Answer:

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f''\left(\frac{1}{2}\right)=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}\Big|_{x=1/2}=\frac{2}{(1−x)^3}\Big|_{x=1/2}=16\) so \(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

32) Evaluate \(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) as \(\displaystyle ∫^1_0f(t) \, dt\) where \(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{10}\)

In exercises 33 - 39, given that \(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), use term-by-term differentiation or integration to find power series for each function centered at the given point.

33) \(f(x)=\ln x\) centered at \(x=1\) (Hint: \(x=1−(1−x)\))

Answer:

\(\displaystyle ∫\sum(1−x)^n\,dx=∫\sum(−1)^n(x−1)^n\,dx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

34) \(\ln(1−x)\) at \(x=0\)

35) \(\ln(1−x^2)\) at \(x=0\)

Answer:

\(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

36) \(f(x)=\dfrac{2x}{(1−x^2)^2}\) at \(x=0\)

37) \(f(x)=\tan^{−1}(x^2)\) at \(x=0\)

Answer:

\(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

38) \(f(x)=\ln(1+x^2)\) at \(x=0\)

39) \(\displaystyle f(x)=∫^x_0\ln t\,dt\) where \(\displaystyle \ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

Answer:

Term-by-term integration gives \(\displaystyle ∫^x_0\ln t\,dt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}\left(\frac{1}{n}−\frac{1}{n+1}\right)(x−1)^{n+1}=(x−1)\ln x+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=x\ln x−x.\)

Exercise \(\PageIndex{11}\)

40) [T] Evaluate the power series expansion \(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\) at \(x=1\) to show that \(\ln(2)\) is the sum of the alternating harmonic series. Use the alternating series test to determine how many terms of the sum are needed to estimate \(\ln(2)\) accurate to within \(0.001,\) and find such an approximation.

41) [T] Subtract the infinite series of \(\ln(1−x)\) from \(\ln(1+x)\) to get a power series for \(\ln\left(\dfrac{1+x}{1−x}\right)\). Evaluate at \(x=\frac{1}{3}\). What is the smallest \(N\) such that the \(N^{\text{th}}\) partial sum of this series approximates \(\ln(2)\) with an error less than \(0.001\)?

Answer:

We have \(\displaystyle \ln(1−x)=−\sum_{n=1}^∞\frac{x^n}{n}\) so \(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\). Thus, \(\displaystyle \ln\left(\frac{1+x}{1−x}\right)=\sum_{n=1}^∞\big(1+(−1)^{n−1}\big)\frac{x^n}{n}=2\sum_{n=1}^∞\frac{x^{2n−1}}{2n−1}\). When \(x=\frac{1}{3}\) we obtain \(\displaystyle \ln(2)=2\sum_{n=1}^∞\frac{1}{3^{2n−1}(2n−1)}\). We have \(\displaystyle 2\sum_{n=1}^3\frac{1}{3^{2n−1}(2n−1)}=0.69300…\), while \(\displaystyle 2\sum_{n=1}^4\frac{1}{3^{2n−1}(2n−1)}=0.69313…\) and \(\ln(2)=0.69314…;\) therefore, \(N=4\).

 

Exercise \(\PageIndex{12}\)

In exercises 42 - 45, using a substitution if indicated, express each series in terms of elementary functions and find the radius of convergence of the sum.

42) \(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

43) \(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

Answer:

\(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−\ln(1−x)\) so \(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}=−\frac{1}{6}\ln(1−x^3)\). The radius of convergence is equal to \(1\) by the ratio test.

44) \(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) using \(y=\dfrac{1}{1+x^2}\)

45) \(\displaystyle \sum_{k=1}^∞2^{−kx}\) using \(y=2^{−x}\)

Answer:

If \(y=2^{−x}\), then \(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). If \(a_k=2^{−kx}\), then \(\dfrac{a_{k+1}}{a_k}=2^{−x}<1\) when \(x>0\). So the series converges for all \(x>0\).

Exercise \(\PageIndex{13}\)

46) Show that, up to powers \(x^3\) and \(y^3\), \(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) satisfies \(E(x+y)=E(x)E(y)\).

47) Differentiate the series \(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) term-by-term to show that \(E(x)\) is equal to its derivative.

Answer:

Answers will vary.

48) Show that if \(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) is a sum of even powers, that is, \(a_n=0\) if \(n\) is odd, then \(\displaystyle F=∫^x_0f(t)\, dt\) is a sum of odd powers, while if \(I\) is a sum of odd powers, then \(F\) is a sum of even powers.

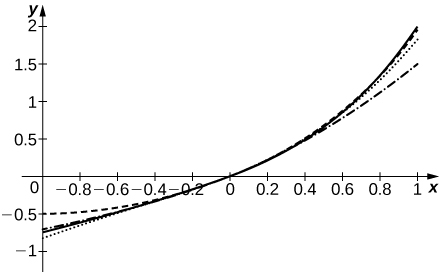
49) [T] Suppose that the coefficients an of the series \(\displaystyle \sum_{n=0}^∞a_nx^n\) are defined by the recurrence relation \(a_n=\dfrac{a_{n−1}}{n}+\dfrac{a_{n−2}}{n(n−1)}\). For \(a_0=0\) and \(a_1=1\), compute and plot the sums \(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) for \(N=2,3,4,5\) on \([−1,1].\)

Answer:

The solid curve is \(S_5\). The dashed curve is \(S_2\), dotted is \(S_3\), and dash-dotted is \(S_4\)

50) [T] Suppose that the coefficients an of the series \(\displaystyle \sum_{n=0}^∞a_nx^n\) are defined by the recurrence relation \(a_n=\dfrac{a_{n−1}}{\sqrt{n}}−\dfrac{a_{n−2}}{\sqrt{n(n−1)}}\). For \(a_0=1\) and \(a_1=0\), compute and plot the sums \(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) for \(N=2,3,4,5\) on \([−1,1]\).

51) [T] Given the power series expansion \(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), determine how many terms \(N\) of the sum evaluated at \(x=−1/2\) are needed to approximate \(\ln(2)\) accurate to within \(1/1000.\) Evaluate the corresponding partial sum \(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).

Answer:

When \(\displaystyle x=−\frac{1}{2}, \;−\ln(2)=\ln\left(\frac{1}{2}\right)=−\sum_{n=1}^∞\frac{1}{n2^n}\). Since \(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\) one has \(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\) whereas \(\ln(2)=0.69314…;\) therefore, \(N=10.\)

52) [T] Given the power series expansion \(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), use the alternating series test to determine how many terms \(N\) of the sum evaluated at \(x=1\) are needed to approximate \(\tan^{−1}(1)=\frac{π}{4}\) accurate to within \(1/1000.\) Evaluate the corresponding partial sum \(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

53) [T] Recall that \(\tan^{−1}\left(\frac{1}{\sqrt{3}}\right)=\frac{π}{6}.\) Assuming an exact value of \(\frac{1}{\sqrt{3}})\), estimate \(\frac{π}{6}\) by evaluating partial sums \(S_N\left(\frac{1}{\sqrt{3}}\right)\) of the power series expansion \(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) at \(x=\frac{1}{\sqrt{3}}\). What is the smallest number \(N\) such that \(6S_N\left(\frac{1}{\sqrt{3}}\right)\) approximates \(π\) accurately to within \(0.001\)? How many terms are needed for accuracy to within \(0.00001\)?

Answer:

\(\displaystyle 6S_N\left(\frac{1}{\sqrt{3}}\right)=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\) One has \(π−6S_4\left(\frac{1}{\sqrt{3}}\right)=0.00101…\) and \(π−6S_5\left(\frac{1}{\sqrt{3}}\right)=0.00028…\) so \(N=5\) is the smallest partial sum with accuracy to within \(0.001.\) Also, \(π−6S_7\left(\frac{1}{\sqrt{3}}\right)=0.00002…\) while \(π−6S_8\left(\frac{1}{\sqrt{3}}\right)=−0.000007…\) so \(N=8\) is the smallest \(N\) to give accuracy to within \(0.00001.\)

 

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.