2.1E: Exercises
- Page ID
- 18545
This page is a draft and is under active development.
Integration by Parts
In using the technique of integration by parts, you must carefully choose which expression is \(u\). For each of the following problems, use the guidelines in this section to choose \(u\). Do not evaluate the integrals.
Exercise \(\PageIndex{1}\)
\(\displaystyle ∫x^3e^{2x}\,dx\)
- Answer
-
\( u=x^3\)
Exercise \(\PageIndex{2}\)
\(\displaystyle ∫x^3\ln(x)\,dx\)
- Answer
-
\( u = ln(x) \)
Exercise \(\PageIndex{3}\)
\(\displaystyle ∫y^3\cos y\,dy\)
- Answer
-
\(u=y^3\)
Exercise \(\PageIndex{4}\)
\(\displaystyle ∫x^2\arctan x\,dx\)
- Answer
-
\( u = \arctan x \)
Exercise \(\PageIndex{5}\)
\(\displaystyle ∫e^{3x}\sin(2x)\,dx\)
- Answer
-
\(u=\sin(2x)\)
In exercises 6 - 37, find the integral by using the simplest method. Not all problems require integration by parts.
Exercise \(\PageIndex{6}\)
\(\displaystyle ∫v\sin v\,dv\)
- Hint
-
\( Let \hspace{5mm} u = v \)
- Answer
-
\( \int v \sin{\left (v \right )}\, dv = - v \cos{\left (v \right )} + \sin{\left (v \right )} + C \)
Exercise \(\PageIndex{7}\)
\(\displaystyle ∫\ln x\,dx\)
- Hint
-
(Hint: \(\displaystyle ∫\ln x\,dx\) is equivalent to \(\displaystyle ∫1⋅\ln(x)\,dx.)\)
- Answer
-
\( \int \ln{\left (x \right )}\, dx = x \ln{\left (x \right )} - x + C \)
Exercise \(\PageIndex{8}\)
\(\displaystyle ∫x\cos x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int x \cos{\left (x \right )}\, dx = x \sin{\left (x \right )} + \cos{\left (x \right )} + C \)
Exercise \(\PageIndex{9}\)
\(\displaystyle ∫\tan^{−1}x\,dx\)
- Hint
-
\( Let \hspace{5mm} u=\tan^{-1}x \)
- Answer
-
\(\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C\)
Exercise \(\PageIndex{10}\)
\(\displaystyle ∫x^2e^x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{2} \)
- Answer
-
\( \int x^{2} e^{x}\, dx = \left(x^{2} - 2 x + 2\right) e^{x} + C \)
Exercise \(\PageIndex{11}\)
\(\displaystyle ∫x\sin(2x)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int x \sin{\left (2 x \right )}\, dx = - \frac{x \cos{\left (2 x \right )}}{2} + \frac{\sin{\left (2 x \right )}}{4} + C \)
Exercise \(\PageIndex{12}\)
\(\displaystyle ∫xe^{4x}\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int x e^{4 x}\, dx = \frac{\left(4 x - 1\right) e^{4 x}}{16} + C \)
Exercise \(\PageIndex{13}\)
\(\displaystyle ∫xe^{−x}\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\(\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C\)
Exercise \(\PageIndex{14}\)
\(\displaystyle ∫x\cos 3x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int x \cos{\left (3 x \right )}\, dx = \frac{x \sin{\left (3 x \right )}}{3} + \frac{\cos{\left (3 x \right )}}{9} + C \)
Exercise \(\PageIndex{15}\)
\(\displaystyle ∫x^2\cos x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{2} \)
- Answer
-
\(\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C\)
Exercise \(\PageIndex{16}\)
\(\displaystyle ∫x\ln x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left ( x \right )} \)
- Answer
-
\( \int x \ln{\left(x \right)}\, dx = \frac{x^{2} \ln{\left(x \right)}}{2} - \frac{x^{2}}{4} + C \)
Exercise \(\PageIndex{17}\)
\(\displaystyle ∫\ln(2x+1)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left (2 x + 1 \right )} \)
- Answer
-
\(\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C\)
Exercise \(\PageIndex{18}\)
\(\displaystyle ∫x^2e^{4x}\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{2} \)
- Answer
-
\( \int x^{2} e^{4 x}\, dx = \frac{\left(8 x^{2} - 4 x + 1\right) e^{4 x}}{32} + C \)
Exercise \(\PageIndex{19}\)
\(\displaystyle ∫e^x\sin x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \sin x \)
- Answer
-
\(\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C\)
Exercise \(\PageIndex{20}\)
\(\displaystyle ∫e^x\cos x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \cos x \)
- Answer
-
\( \int e^{x} \cos{\left (x \right )}\, dx = \frac{e^{x} \sin{\left (x \right )}}{2} + \frac{e^{x} \cos{\left (x \right )}}{2} + C \)
Exercise \(\PageIndex{21}\)
\(\displaystyle ∫xe^{−x^2}\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\(\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C\)
Exercise \(\PageIndex{22}\)
\(\displaystyle ∫x^2e^{−x}\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{2} \)
- Answer
-
\( \int x^{2} e^{- x}\, dx = \left(- x^{2} - 2 x - 2\right) e^{- x} + C \)
Exercise \(\PageIndex{23}\)
\(\displaystyle ∫\sin(\ln(2x))\,dx\)
- Hint
-
\( Let \hspace{2mm} u = \sin{\left (\ln{\left (2 x \right )} \right )} \)
\( Second \hspace{2mm} Integration: Let \hspace{2mm} u = \sin{\left (\ln{\left (2 x \right )} \right )} \)
- Answer
-
\(\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C\)
Exercise \(\PageIndex{24}\)
\(\displaystyle ∫\cos(\ln x)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \cos{\left (\ln{\left (x \right )} \right )} \)
- Answer
-
\( \int \cos{\left (\ln{\left (x \right )} \right )}\, dx = \frac{x \sin{\left (\ln{\left (x \right )} \right )}}{2} + \frac{x \cos{\left (\ln{\left (x \right )} \right )}}{2} + C \)
Exercise \(\PageIndex{25}\)
\(\displaystyle ∫(\ln x)^2\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \left ( \ln{x}\right )^{2} \)
- Answer
-
\(\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C\)
Exercise \(\PageIndex{26}\)
\(\displaystyle ∫\ln(x^2)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left (x^{2} \right )} \)
- Answer
-
\( \int \ln{\left (x^{2} \right )}\, dx = x \ln{\left (x^{2} \right )} - 2 x + C \)
Exercise \(\PageIndex{27}\)
\(\displaystyle ∫x^2\ln x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln\left (x \right ) \)
- Answer
-
\(\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C\)
Exercise \(\PageIndex{28}\)
\(\displaystyle ∫\sin^{−1}x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \sin^{-1}x \)
- Answer
-
\( \int \sin^{-1}{\left(x \right)}\, dx = x \sin^{-1}{\left(x \right)} + \sqrt{1 - x^{2}} + C \)
Exercise \(\PageIndex{29}\)
\(\displaystyle ∫\cos^{−1}(2x)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \cos^{-1}(2x) \)
- Answer
-
\(\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C\)
Exercise \(\PageIndex{30}\)
\(\displaystyle ∫x\arctan x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \arctan x \)
- Answer
-
\( \int x \arctan{\left(x \right)}\, dx = \frac{x^{2} \arctan{\left(x \right)}}{2} - \frac{x}{2} + \frac{\arctan{\left(x \right)}}{2} + C \)
Exercise \(\PageIndex{31}\)
\(\displaystyle ∫x^2\sin x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{2} \)
- Answer
-
\(\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C\)
Exercise \(\PageIndex{32}\)
\(\displaystyle ∫x^3\cos x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{3} \)
- Answer
-
\( \int x^{3} \cos{\left (x \right )}\, dx = x^{3} \sin{\left (x \right )} + 3 x^{2} \cos{\left (x \right )} - 6 x \sin{\left (x \right )} - 6 \cos{\left (x \right )} + C \)
Exercise \(\PageIndex{33}\)
\(\displaystyle ∫x^3\sin x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{3} \)
- Answer
-
\(\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C\)
Exercise \(\PageIndex{34}\)
\(\displaystyle ∫x^3e^x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x^{3} \)
- Answer
-
\( \int x^{3} e^{x}\, dx = \left(x^{3} - 3 x^{2} + 6 x - 6\right) e^{x} + C \)
Exercise \(\PageIndex{35}\)
\(\displaystyle ∫x\sec^{−1}x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \sec^{-1}(x) \)
- Answer
-
\(\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C\)
Exercise \(\PageIndex{36}\)
\(\displaystyle ∫x\sec^2x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int x \sec^{2}{\left(x \right)}\, dx = x \tan{\left(x \right)} -\ln |\sec{\left(x \right)}|+ C \)
Exercise \(\PageIndex{37}\)
\(\displaystyle ∫x\cosh x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\(\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C\)
In exercises 38 - 46, compute the definite integrals. Use a graphing utility to confirm your answers.
Exercise \(\PageIndex{38}\)
\(\displaystyle ∫^1_{1/e}\ln x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln x \)
- Answer
-
\(\displaystyle ∫^1_{1/e}\ln x\,dx = 2/e -1 \)
Exercise \(\PageIndex{39}\)
\(\displaystyle ∫^1_0xe^{−2x}\,dx\) (Express the answer in exact form.)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\(\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}\)
Exercise \(\PageIndex{40}\)
\(\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad \)
- Hint
-
\( \text{let}\, u=\sqrt{x} \)
- Answer
-
\( \int\limits_{0.0}^{1.0} e^{\sqrt{x}}\, dx = 2 \)
Exercise \(\PageIndex{41}\)
\(\displaystyle ∫^e_1\ln(x^2)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left(x^{2} \right)} \)
- Answer
-
\(\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2\)
Exercise \(\PageIndex{42}\)
\(\displaystyle ∫^π_0x\cos x\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left(x \right)} \)
- Answer
-
\(\displaystyle ∫^π_0x\cos x\,dx = -2 \)
Exercise \(\PageIndex{43}\)
\(\displaystyle ∫^π_{−π}x\sin x\,dx\) (Express the answer in exact form.)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\(\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi\)
Exercise \(\PageIndex{44}\)
\(\displaystyle ∫^3_0\ln(x^2+1)\,dx\) (Express the answer in exact form.)
- Hint
-
\( Let \hspace{5mm} u = \ln{\left(x^{2} + 1 \right)} \)
Second hint: \( \hspace{2mm} x^2 = x^2 + 1 - 1 \)
- Answer
-
\( \int\limits_{0.0}^{3.0} \log{\left(x^{2} + 1 \right)}\, dx = 3.4058 \)
Exercise \(\PageIndex{45}\)
\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx\) (Express the answer in exact form.)
- Hint
-
\( Let \hspace{5mm} u = x^2 \)
- Answer
-
\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π\)
Exercise \(\PageIndex{46}\)
\(\displaystyle ∫^1_0x5^x\,dx\) (Express the answer using five significant digits.)
- Hint
-
\( Let \hspace{5mm} u = x \)
- Answer
-
\( \int\limits_{0.0}^{1.0} 5^{x} x\, dx = 1.1764 \)
Exercise \(\PageIndex{47}\)
Evaluate \(\displaystyle ∫\cos x\ln(\sin x)\,dx\)
- Hint
-
\( Let \hspace{5mm} u = \ln (\sin x) \)
- Answer
-
\(\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C\)
In exercises 48 - 50, derive the following formulas using the technique of integration by parts. Assume that \(n\) is a positive integer. These formulas are called reduction formulas because the exponent in the \(x\) term has been reduced by one in each case. The second integral is simpler than the original integral.
Exercise \(\PageIndex{48}\)
\(\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx\)
- Hint
-
Let \( u = x^n \)
- Answer
-
Answers vary
Exercise \(\PageIndex{49}\)
\(\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx\)
- Hint
-
Find the recurrence integral.
- Answer
-
Answers vary
Exercise \(\PageIndex{50}\)
\(\displaystyle ∫x^n\sin x\,dx=\)
- Hint
-
Recurrence Integral: \( I_n= \displaystyle ∫x^n \sin(x)\, dx = −x^n \cos(x)+nx^{n−1} \sin(x)−n(n−1)I_{n−2} \)
- Answer
-
Answers vary.
Exercise \(\PageIndex{51}\)
Integrate \(\displaystyle ∫2x\sqrt{2x−3}\,dx\) using two methods:
a. Using parts, letting \(dv=\sqrt{2x−3}\,dx\)
b. Substitution, letting \(u=2x−3\)
- Answer
-
a. \(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
b. \(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
In exercises 52 - 57, state whether you would use integration by parts to evaluate the integral. If so, identify \(u\) and \(dv\). If not, describe the technique used to perform the integration without actually doing the problem.
Exercise \(\PageIndex{52}\)
\(\displaystyle ∫x\ln x\,dx\)
- Answer
-
Integration by parts. Choose \(u\) to be \(\ln x\), then \( dv=x\,dx. \)
Exercise \(\PageIndex{53}\)
\(\displaystyle ∫\frac{\ln^2x}{x}\,dx\)
- Answer
-
Do not use integration by parts. Choose \(u\) to be \(\ln x\), and the integral is of the form \(\displaystyle ∫u^2\,du.\)
Exercise \(\PageIndex{54}\)
\(\displaystyle ∫xe^x\,dx\)
- Answer
-
Integration by parts. Choose \(u\) to be \(x\), then \( dv=e^x\,dx. \)
Exercise \(\PageIndex{55}\)
\(\displaystyle ∫xe^{x^2−3}\,dx\)
- Answer
-
Do not use integration by parts. Let \(u=x^2−3\), and the integral can be put into the form \(∫e^u\,du\).
Exercise \(\PageIndex{56}\)
\(\displaystyle ∫x^2\sin x\,dx\)
- Answer
-
Integration by parts. Let \(u=x^2\), then \( dv= sin x\, dx \)
Exercise \(\PageIndex{57}\)
\(\displaystyle ∫x^2\sin(3x^3+2)\,dx\)
- Answer
-
Do not use integration by parts. Choose \(u\) to be \(u=3x^3+2\) and the integral can be put into the form \(\displaystyle ∫\sin(u)\,du.\)
In exercises 58-59, sketch the region bounded above by the curve, the \(x\)-axis, and \(x=1\), and find the area of the region. Provide the exact form or round answers to the number of places indicated.
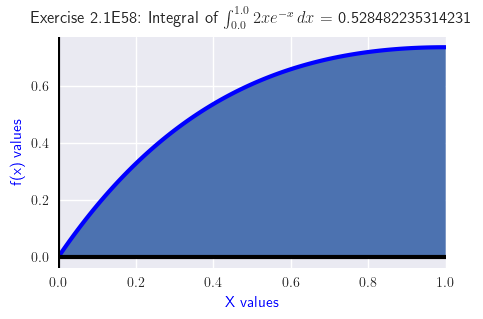
Exercise \(\PageIndex{58}\)
\(y=2xe^{−x}\) (Approximate answer to four decimal places.)
- Answer
-
\( \int_{0.0}^{1.0} 2 x e^{- x}\, dx = 0.5285 \)
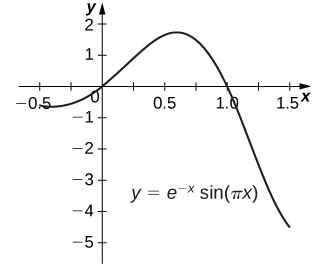
Exercise \(\PageIndex{59}\)
\(y=e^{−x}\sin(πx)\) (Approximate answer to five decimal places.)
- Answer
-
The area under graph is \(0.39535 \, \text{units}^2.\)
In exercises 60 - 61, find the volume generated by rotating the region bounded by the given curves about the specified line. Express the answers in exact form or approximate to the number of decimal places indicated.
Exercise \(\PageIndex{60}\)
\(y=\sin x,\,y=0,\,x=2π,\,x=3π;\) about the \(y\)-axis (Express the answer in exact form.)
- Answer
-
\( V = \int_{2π}^{3π} 2πx \sin x\, dx = 10π \text{units}^3 \)
Exercise \(\PageIndex{61}\)
\(y=e^{−x}, \,y=0,\,x=−1, \, x=0;\) about \(x=1\) (Express the answer in exact form.)
- Answer
-
\(V = 2πe \, \text{units}^3\)
Exercise \(\PageIndex{62}\)
A particle moving along a straight line has a velocity of \(v(t)=t^2e^{−t}\) after \(t\) sec. How far does it travel in the first 2 sec? (Assume the units are in feet and express the answer in exact form.)
- Answer
-
\( \int_{0}^{2} t^{2} e^{- t}\, dt = 2+ \frac{-10}{e^2}\text{ft.}\)
Exercise \(\PageIndex{63}\)
Find the area under the graph of \(y=\sec^3x\) from \(x=0\) to \(x=1\). (Round the answer to two significant digits.)
- Answer
-
\(A= 2.05 \, \text{units}^2\)
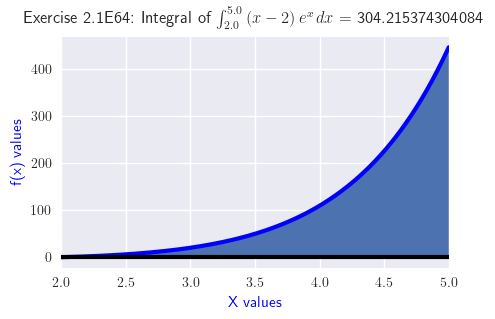
Exercise \(\PageIndex{64}\)
Find the area between \(y=(x−2)e^x\) and the \(x\)-axis from \(x=2\) to \(x=5\). (Express the answer in exact form.)
- Answer
-
\( \int_{2}^{5} \left(x - 2\right) e^{x}\, dx = 2e^5 + e^2 \)
Exercise \(\PageIndex{65}\)
Find the area of the region enclosed by the curve \(y=x\cos x\) and the \(x\)-axis for \(\frac{11π}{2}≤x≤\frac{13π}{2}.\) (Express the answer in exact form.)
- Answer
-
\(A = 12π \, \text{units}^2\)
Exercise \(\PageIndex{66}\)
Find the volume of the solid generated by revolving the region bounded by the curve \(y=\ln x\), the \(x\)-axis, and the vertical line \(x=e^2\) about the \(x\)-axis. (Express the answer in exact form.)
- Answer
-
\( \int_{1}^{π^2} π\left( \ln x \right)^2 \, dx = 2πe^2 - 2π \)
Exercise \(\PageIndex{67}\)
Find the volume of the solid generated by revolving the region bounded by the curve \(y=4\cos x\) and the \(x\)-axis, \(\frac{π}{2}≤x≤\frac{3π}{2},\) about the \(x\)-axis. (Express the answer in exact form.)
- Answer
-
\(V = 8π^2 \, \text{units}^3\)
Exercise \(\PageIndex{68}\)
Find the volume of the solid generated by revolving the region in the first quadrant bounded by \(y=e^x\) and the \(x\)-axis, from \(x=0\) to \(x=\ln(7)\), about the \(y\)-axis. (Express the answer in exact form.)
- Answer
-
\( \int_{0}^{\ln 7} 2 \pi x e^{x}\, dx = 2.0 \pi(7 \ln(7) -6) \)


