2.6: Improper Integrals
- Page ID
- 10270
This page is a draft and is under active development.
Is the area between the graph of \(f(x)=\frac{1}{x}\) and the x-axis over the interval \([1,+∞)\) finite or infinite? If this same region is revolved about the x-axis, is the volume finite or infinite? Surprisingly, the area of the region described is infinite, but the volume of the solid obtained by revolving this region about the x-axis is finite.
In this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals of these types are called improper integrals. We examine several techniques for evaluating improper integrals, all of which involve taking limits.
Integrating over an Infinite Interval
How should we go about defining an integral of the type \(\int ^{+∞}_af(x)dx?\) We can integrate \(\int ^t_af(x)dx\) for any value of \(t\), so it is reasonable to look at the behavior of this integral as we substitute larger values of \(t\). Figure shows that \(\int ^t_af(x)dx\) may be interpreted as area for various values of \(t\). In other words, we may define an improper integral as a limit, taken as one of the limits of integration increases or decreases without bound.

Definition: improper integral
- Let \(f(x)\) be continuous over an interval of the form \([a,+∞)\). Then \[\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx, \label{improper1}\] provided this limit exists.
- Let \(f(x)\) be continuous over an interval of the form \((−∞,b]\). Then \[\int ^b_{−∞}f(x)dx=\lim_{t→−∞}\int ^b_tf(x)dx, \label{improper2}\] provided this limit exists.
In each case, if the limit exists, then the improper integral is said to converge. If the limit does not exist, then the improper integral is said to diverge.
- Let \(f(x)\) be continuous over \((−∞,+∞)\). Then \[\int ^{+∞}_{−∞}f(x)dx=\int ^0_{−∞}f(x)dx+\int ^{+∞}_0f(x)dx, \label{improper3}\] provided that \(\int ^0_{−∞}f(x)dx\) and \(\int ^{+∞}_0f(x)dx\) both converge. If either of these two integrals diverge, then \(\int ^{+∞}_{−∞}f(x)dx\) diverges. (It can be shown that, in fact, \(\int ^{+∞}_{−∞}f(x)dx=\int ^a_{−∞}f(x)dx+\int ^{+∞}_af(x)dx\) for any value of a.).
In our first example, we return to the question we posed at the start of this section: Is the area between the graph of \(f(x)=\frac{1}{x}\) and the \(x\)-axis over the interval \([1,+∞)\) finite or infinite?
Example \(\PageIndex{1}\): Finding an Area
Determine whether the area between the graph of \(f(x)=\frac{1}{x}\) and the x-axis over the interval \([1,+∞)\) is finite or infinite.
Solution
We first do a quick sketch of the region in question, as shown in Figure \(\PageIndex{2}\).
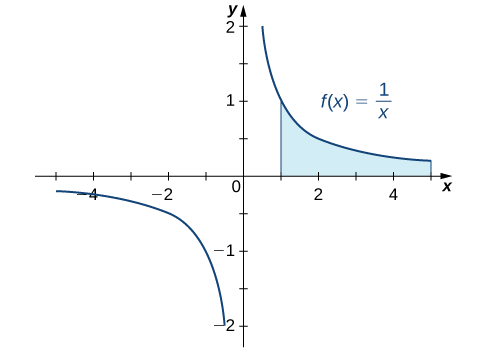
We can see that the area of this region is given by
\[A=\int ^∞_1\frac{1}{x}dx. \nonumber\]
which can be evaluated using Equation \ref{improper1}:
\[ \begin{align} A &=\int ^∞_1\frac{1}{x}dx \nonumber \\[5pt] &=\lim_{t→+∞}\int ^t_1\frac{1}{x}dx \tag{Rewrite the improper integral as a limit} \\[5pt] &=\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[5pt] &=\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[5pt] &=+∞. \tag{Evaluate the limit.} \end{align}\]
Since the improper integral diverges to \(+∞,\) the area of the region is infinite.
Example \(\PageIndex{2}\): Finding a Volume
Find the volume of the solid obtained by revolving the region bounded by the graph of \(f(x)=\frac{1}{x}\) and the \(x\)-axis over the interval \([1,+∞)\) about the \(x\)-axis.
Solution
The solid is shown in Figure \(\PageIndex{3}\). Using the disk method, we see that the volume V is
\[V=π\int ^{+∞}_1\frac{1}{x^2}dx.\]
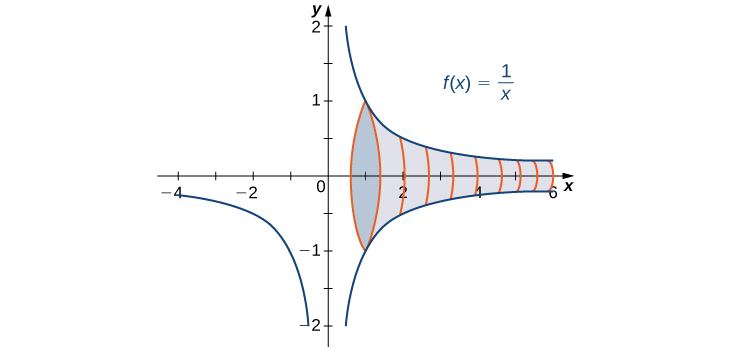
Then we have
\(V=π\int ^{+∞}_1\frac{1}{x^2}dx\)
\(=π\lim_{t→+∞}\int ^t_1\frac{1}{x^2}dx\) Rewrite as a limit
\(=π\lim_{t→+∞}−\frac{1}{x}∣^t_1\) Find the antiderivative.
\(=π\lim_{t→+∞}(−\frac{1}{t}+1)\) Evaluate the antiderivative.
\(=π\)
The improper integral converges to \(π\). Therefore, the volume of the solid of revolution is \(π\).
In conclusion, although the area of the region between the x-axis and the graph of \(f(x)=1/x\) over the interval \([1,+∞)\) is infinite, the volume of the solid generated by revolving this region about the x-axis is finite. The solid generated is known as Gabriel’s Horn.
Note: Gabriel's horn (also called Torricelli's trumpet) is a geometric figure which has infinite surface area, but finite volume. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli in the 17th century.
Example \(\PageIndex{3}\): Traffic Accidents in a City
Suppose that at a busy intersection, traffic accidents occur at an average rate of one every three months. After residents complained, changes were made to the traffic lights at the intersection. It has now been eight months since the changes were made and there have been no accidents. Were the changes effective or is the 8-month interval without an accident a result of chance?

Probability theory tells us that if the average time between events is \(k\), the probability that \(X\), the time between events, is between \(a\) and \(b\) is given by
\[(P(a≤x≤b)=\int ^b_af(x)dx \nonumber\]
where
\[f(x)=\begin{cases}0&ifx<0\\ke^{−kx}&ifx≥0\end{cases}. \nonumber\]
Thus, if accidents are occurring at a rate of one every 3 months, then the probability that \(X\), the time between accidents, is between \(a\) and \(b\) is given by
\[P(a≤x≤b)=\int ^b_af(x)dx \nonumber\]
where \[f(x)=\begin{cases}0&ifx<0\\3e^{−3x}&ifx≥0\end{cases}. \nonumber\]
To answer the question, we must compute \(P(X≥8)=\int ^{+∞}_83e^{−3x}dx\) and decide whether it is likely that 8 months could have passed without an accident if there had been no improvement in the traffic situation.
Solution
We need to calculate the probability as an improper integral:
\(P(X≥8)=\int ^{+∞}_83e^{−3x}dx\)
\(=\lim_{t→+∞}\int ^t_83e^{−3x}dx\)
\(=\lim_{t→+∞}−e^{−3x}∣^t_8\)
\(=\lim_{t→+∞}(−e^{−3t}+e^{−24})\)
\(≈3.8×10^{−11}.\)
The value \(3.8×10^{−11}\) represents the probability of no accidents in 8 months under the initial conditions. Since this value is very, very small, it is reasonable to conclude the changes were effective.
Example \(\PageIndex{4}\): Evaluating an Improper Integral over an Infinite Interval
Evaluate \[\int ^0_{−∞}\frac{1}{x^2+4}dx.\] State whether the improper integral converges or diverges.
Solution
Begin by rewriting \(\int ^0_{−∞}\frac{1}{x^2+4}dx\) as a limit using Equation from the definition. Thus,
\(\int ^0_{−∞}\frac{1}{x^2+4}dx=\lim_{t→−∞}\int ^0_t\frac{1}{x^2+4}dx\) Rewrite as a limit.
\(=\lim_{t→−∞}tan^{−1}\frac{x}{2}∣^0_t\) Find the antiderivative.
\(=\lim_{t→−∞}(tan^{−1}0−tan^{−1}\frac{t}{2})\) Evaluate the antiderivative.
\(=\frac{π}{2}\). Evaluate the limit and simplify.
The improper integral converges to \(\frac{π}{2}.\)
Example \(\PageIndex{5}\): Evaluating an Improper Integral on \((−∞,+∞)\)
Evaluate \[\int ^{+∞}_{−∞}xe^xdx.\] State whether the improper integral converges or diverges.
Solution
Start by splitting up the integral:
\[\int ^{+∞}_{−∞}xe^xdx=\int ^0_{−∞}xe^xdx+\int ^{+∞}_0xe^xdx.\]
If either \(\int ^0_{−∞}xe^xdx\) or \(\int ^{+∞}_0xe^xdx\) diverges, then \(\int ^{+∞}_{−∞}xe^xdx\) diverges. Compute each integral separately. For the first integral,
\(\int ^0_{−∞}xe^xdx=\lim_{t→−∞}\int ^0_txe^xdx\) Rewrite as a limit.
\(=\lim_{t→−∞}(xe^x−e^x)∣^0_t\) Use integration by parts to find the antiderivative. (Here \(u=x\) and \(dv=e^x\).)
\(=\lim_{t→−∞}(−1−te^t+e^t)\) Evaluate the antiderivative.
\(=−1.\)
Evaluate the limit. Note: \(\lim_{t→−∞}te^t\) is indeterminate of the form \(0⋅∞\).Thus, \(\lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0\) byL’Hôpital’s Rule.
The first improper integral converges. For the second integral,
\(\int ^{+∞}_0xe^xdx=\lim_{t→+∞}\int ^t_0xe^xdx\) Rewrite as a limit.
\(=\lim_{t→+∞}(xe^x−e^x)∣^t_0\) Find the antiderivative.
\(=\lim_{t→+∞}(te^t−e^t+1)\) Evaluate the antiderivative.
\(=\lim_{t→+∞}((t−1)e^t+1)\) Rewrite.(\(te^t−e^t\) is indeterminate.)
\(=+∞.\) Evaluate the limit.
Thus, \(\int ^{+∞}_0xe^xdx\) diverges. Since this integral diverges, \(\int ^{+∞}_{−∞}xe^xdx\) diverges as well.
Exercise \(\PageIndex{1}\)
Evaluate \[\int ^{+∞}_{−3}e^{−x}dx.\] State whether the improper integral converges or diverges.
- Hint
-
\[\int ^{+∞}_{−3}e^{−x}dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}dx\]
- Answer
-
\(e^3\), converges
Integrating a Discontinuous Integrand
Now let’s examine integrals of functions containing an infinite discontinuity in the interval over which the integration occurs. Consider an integral of the form \(\int ^b_af(x)dx,\) where \(f(x)\) is continuous over \([a,b)\) and discontinuous at \(b\). Since the function \(f(x)\) is continuous over \([a,t]\) for all values of \(t\) satisfying \(a<t<b\), the integral \(\int ^t_af(x)dx\) is defined for all such values of \(t\). Thus, it makes sense to consider the values of \(\int ^t_af(x)dx\) as \(t\) approaches \(b\) for \(a<t<b\). That is, we define \(\int ^b_af(x)dx=\lim_{t→b^−}\int ^t_af(x)dx\), provided this limit exists. Figure illustrates \(\int ^t_af(x)dx\) as areas of regions for values of \(t\) approaching \(b\).
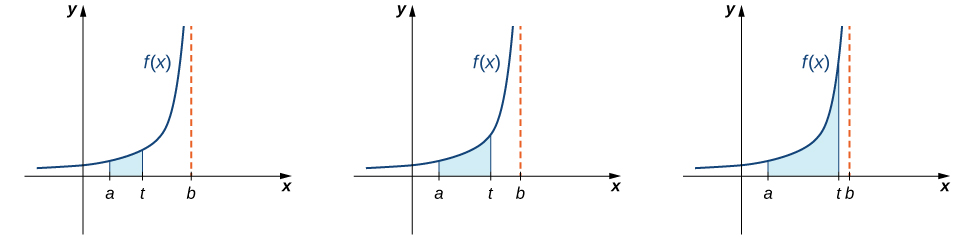
We use a similar approach to define \(\int ^b_af(x)dx\), where \(f(x)\) is continuous over \((a,b]\) and discontinuous at \(a\). We now proceed with a formal definition.
Definition
- Let \(f(x)\) be continuous over \([a,b)\). Then, \[\int ^b_af(x)dx=\lim_{t→b^−}\int ^t_af(x)dx.\]
- Let \(f(x)\) be continuous over \((a,b]\). Then, \[\int ^b_af(x)dx=\lim_{t→a^+}\int ^b_tf(x)dx.\] In each case, if the limit exists, then the improper integral is said to converge. If the limit does not exist, then the improper integral is said to diverge.
- If \(f(x)\) is continuous over \([a,b]\) except at a point \(c\) in \((a,b)\), then \[\int ^b_af(x)dx=\int ^c_af(x)dx+\int ^b_cf(x)dx,\] provided both \(\int ^c_af(x)dx\) and \(\int ^b_cf(x)dx\) converge. If either of these integrals diverges, then \(\int ^b_af(x)dx\) diverges.
The following examples demonstrate the application of this definition.
Example \(\PageIndex{6}\): Integrating a Discontinuous Integrand
Evaluate \(\int ^4_0\frac{1}{\sqrt{4−x}}dx,\) if possible. State whether the integral converges or diverges.
Solution
The function \(f(x)=\frac{1}{\sqrt{4−x}}\) is continuous over \([0,4)\) and discontinuous at 4. Using Equation from the definition, rewrite \(\int ^4_0\frac{1}{\sqrt{4−x}}dx\) as a limit:
\(\int ^4_0\frac{1}{\sqrt{4−x}}dx=\lim_{t→4^−}\int ^t_0\frac{1}{\sqrt{4−x}}dx\) Rewrite as a limit.
\(=\lim_{t→4^−}(−2\sqrt{4−x})∣^t_0\) Find the antiderivative.
\(=\lim_{t→4^−}(−2\sqrt{4−t}+4)\) Evaluate the antiderivative.
\(=4.\) Evaluate the limit.
The improper integral converges.
Example \(\PageIndex{7}\): Integrating a Discontinuous Integrand
Evaluate \(\int ^2_0x\ln xdx.\) State whether the integral converges or diverges.
Solution
Since \(f(x)=x\ln x\) is continuous over \((0,2]\) and is discontinuous at zero, we can rewrite the integral in limit form using Equation:
\(\int ^2_0x\ln xdx=\lim_{t→0^+}\int ^2_tx\ln xdx\) Rewrite as a limit.
\(=\lim_{t→0^+}(\frac{1}{2}x^2\ln x−\frac{1}{4}x^2)∣^2_t\) Evaluate \(\int x\ln xdx\) using integration by parts with \(u=\ln x\) and \(dv=x.\)
\(=\lim_{t→0^+}(2\ln 2−1−\frac{1}{2}t^2\ln t+\frac{1}{4}t^2)\). Evaluate the antiderivative.
\(=2\ln 2−1.\) Evaluate the limit. \(\lim_{t→0^+}t^2\ln tis\) indeterminate.
To evaluate it, rewrite as a quotient and applyL’Hôpital’s rule.
The improper integral converges.
Example \(\PageIndex{8}\): Integrating a Discontinuous Integrand
Evaluate \(\int ^1_{−1}\frac{1}{x^3}dx.\) State whether the improper integral converges or diverges.
Solution
Since \(f(x)=1/x^3\) is discontinuous at zero, using Equation, we can write
\(\int ^1_{−1}\frac{1}{x^3}dx=\int ^0_{−1}\frac{1}{x^3}dx+\int ^1_0\frac{1}{x^3}dx.\)
If either of the two integrals diverges, then the original integral diverges. Begin with \(\int ^0_{−1}\frac{1}{x^3}dx\):
\(\int ^0_{−1}\frac{1}{x^3}dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}dx\) Rewrite as a limit.
\(=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}\) Find the antiderivative.
\(=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})\) Evaluate the antiderivative.
\(=+∞.\) Evaluate the limit.
Therefore, \(\int ^0_{−1}\frac{1}{x^3}dx\) diverges. Since \(\int ^0_{−1}\frac{1}{x^3}dx\) diverges, \(\int ^1_{−1}\frac{1}{x^3}dx\) diverges.
Exercise \(\PageIndex{2}\)
Evaluate \(\int ^2_0\frac{1}{x}dx.\) State whether the integral converges or diverges.
- Hint
-
Write \(\int ^2_0\frac{1}{x}dx\) in limit form using Equation.
- Answer
-
\(+∞\), diverges
A Comparison Theorem
It is not always easy or even possible to evaluate an improper integral directly; however, by comparing it with another carefully chosen integral, it may be possible to determine its convergence or divergence. To see this, consider two continuous functions \(f(x)\) and \(g(x)\) satisfying \(0≤f(x)≤g(x)\) for \(x≥a\) (Figure). In this case, we may view integrals of these functions over intervals of the form \([a,t]\) as areas, so we have the relationship
\[ 0≤\int ^t_af(x)dx≤\int ^t_ag(x)dx\]
for \(t≥a\).
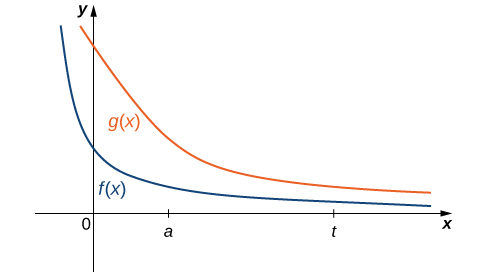
Thus, if
\[\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx=+∞,\]
then
\[\int ^{+∞}_ag(x)dx=\lim_{t→+∞}\int ^t_ag(x)dx=+∞\]
as well. That is, if the area of the region between the graph of \(f(x)\) and the x-axis over \([a,+∞)\) is infinite, then the area of the region between the graph of \(g(x)\) and the x-axis over \([a,+∞)\) is infinite too.
On the other hand, if
\[\int ^{+∞}_ag(x)dx=\lim_{t→+∞}\int ^t_ag(x)dx=L\]
for some real number \(L\), then
\[\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx\]
must converge to some value less than or equal to \(L\), since \(\int ^t_af(x)dx\) increases as \(t\) increases and \(\int ^t_af(x)dx≤L\) for all \(t≥a.\)
If the area of the region between the graph of \(g(x)\) and the x-axis over \([a,+∞)\) is finite, then the area of the region between the graph of \(f(x)\) and the x-axis over \([a,+∞)\) is also finite.
These conclusions are summarized in the following theorem.
A Comparison Theorem
Let \(f(x)\) and \(g(x)\) be continuous over \([a,+∞).\) Assume that \(0≤f(x)≤g(x)\) for \(x≥a.\)
- If \[\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx=+∞,\] then \[\int ^{+∞}_ag(x)dx=\lim_{t→+∞}\int ^t_ag(x)dx=+∞.\]
- If \[\int ^{+∞}_ag(x)dx=\lim_{t→+∞}\int ^t_ag(x)dx=L,\] where \(L\) is a real number, then \[\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx=M\] for some real number \(M≤L.\)
Example \(\PageIndex{9}\): Applying the Comparison Theorem
Use a comparison to show that
\[\int ^{+∞}_1\frac{1}{xe^x}dx \nonumber\]
converges.
Solution
We can see that
\[0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x},\]
so if \(\int ^{+∞}_1e^{−x}dx\) converges, then so does \(\int ^{+∞}_1\frac{1}{xe^x}dx\). To evaluate \(\int ^{+∞}_1e^{−x}dx,\) first rewrite it as a limit:
\(\int ^{+∞}_1e^{−x}dx=\lim_{t→+∞}\int ^t_1e^{−x}dx\)
\(=\lim_{t→+∞}(−e^{−x})∣^t_1\)
\(=\lim_{t→+∞}(−e^{−t}+e^1)\)
\(=e^1.\)
Since \(\int ^{+∞}_1e^{−x}dx\) converges, so does \(\int ^{+∞}_1\frac{1}{xe^x}dx.\)
Example \(\PageIndex{10}\): Applying the Comparison Theorem
Use the comparison theorem to show that \(\int ^{+∞}_1\frac{1}{x^p}dx\) diverges for all \(p<1\).
Solution
For \(p<1, 1/x≤1/(x^p)\) over \([1,+∞).\) In Example \(\PageIndex{9}\), we showed that \(\int ^{+∞}_1\frac{1}{x}dx=+∞.\) Therefore, \(\int ^{+∞}_1\frac{1}{x^p}dx\) diverges for all \(p<1\).
Exercise \(\PageIndex{3}\)
Use a comparison to show that \(\int ^{+∞}_e\frac{\ln x}{x}dx\) diverges.
- Hint
-
\(\frac{1}{x}≤\frac{\ln x}{x}\) on \([e,+∞)\)
- Answer
-
Since \(\int ^{+∞}_e\frac{1}{x}dx=+∞,\) \(\int ^{+∞}_e\frac{\ln x}{x}dx\) diverges.
Laplace Transforms
In the last few chapters, we have looked at several ways to use integration for solving real-world problems. For this next project, we are going to explore a more advanced application of integration: integral transforms. Specifically, we describe the Laplace transform and some of its properties. The Laplace transform is used in engineering and physics to simplify the computations needed to solve some problems. It takes functions expressed in terms of time and transforms them to functions expressed in terms of frequency. It turns out that, in many cases, the computations needed to solve problems in the frequency domain are much simpler than those required in the time domain.
The Laplace transform is defined in terms of an integral as
\[L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt.\]
Note that the input to a Laplace transform is a function of time, \(f(t),\) and the output is a function of frequency, \(F(s)\). Although many real-world examples require the use of complex numbers (involving the imaginary number \(i=\sqrt{−1}),\) in this project we limit ourselves to functions of real numbers.
Let’s start with a simple example. Here we calculate the Laplace transform of \(f(t)=t\). We have
\{L{t}=\int ^∞_0te^{−st}dt.\}
This is an improper integral, so we express it in terms of a limit, which gives
\{L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt.\}
Now we use integration by parts to evaluate the integral. Note that we are integrating with respect to t, so we treat the variable s as a constant. We have
\(u=t\) \(du=dt\) \(dv=e^{−st}dt\) \(v=−\frac{1}{s}e^{−st}\).
Then we obtain
\(\lim_{z→∞}\int ^z_0te^{−st}dt=\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt]\)
\(=\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt]\)
\(=\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0]\)
\(=\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]]\)
\(=\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2}\)
\(=0−0+\frac{1}{s^2}\)
\(=\frac{1}{s^2}.\)
- Calculate the Laplace transform of \(f(t)=1.\)
- Calculate the Laplace transform of \(f(t)=e^{−3t}.\)
- Calculate the Laplace transform of \(f(t)=t^2\). (Note, you will have to integrate by parts twice.)
Laplace transforms are often used to solve differential equations. Differential equations are not covered in detail until later in this book; but, for now, let’s look at the relationship between the Laplace transform of a function and the Laplace transform of its derivative.
Let’s start with the definition of the Laplace transform. We have
\(L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt.\)
4. Use integration by parts to evaluate \(\lim_{z→∞}\int ^z_0e^{−st}f(t)dt\). (Let \(u=f(t)\) and \(dv=e^{−st}dt\).)
After integrating by parts and evaluating the limit, you should see that
\(L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}].\)
Then,
\(L{f′(t)}=sL{f(t)}−f(0).\)
Thus, differentiation in the time domain simplifies to multiplication by s in the frequency domain.
The final thing we look at in this project is how the Laplace transforms of \(f(t)\) and its antiderivative are related. Let \(g(t)=\int ^t_0f(u)du.\) Then,
\(L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt.\)
5. Use integration by parts to evaluate \(\lim_{z→∞}\int ^z_0e^{−st}g(t)dt.\) (Let \(u=g(t)\) and \(dv=e^{−st}dt\). Note, by the way, that we have defined \(g(t), du=f(t)dt.\))
As you might expect, you should see that
\(L{g(t)}=\frac{1}{s}⋅L{f(t)}.\)
Integration in the time domain simplifies to division by s in the frequency domain.
Key Concepts
- Integrals of functions over infinite intervals are defined in terms of limits.
- Integrals of functions over an interval for which the function has a discontinuity at an endpoint may be defined in terms of limits.
- The convergence or divergence of an improper integral may be determined by comparing it with the value of an improper integral for which the convergence or divergence is known.
Key Equations
- Improper integrals
\(\int ^{+∞}_af(x)dx=\lim_{t→+∞}\int ^t_af(x)dx\)
\(\int ^b_{−∞}f(x)dx=\lim_{t→−∞}\int ^b_tf(x)dx\)
\(\int ^{+∞}_{−∞}f(x)dx=\int ^0_{−∞}f(x)dx+\int ^{+∞}_0f(x)dx\)
Glossary
- improper integral
- an integral over an infinite interval or an integral of a function containing an infinite discontinuity on the interval; an improper integral is defined in terms of a limit. The improper integral converges if this limit is a finite real number; otherwise, the improper integral diverges
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

