3.1: Basic Concepts
- Page ID
- 15013
This page is a draft and is under active development.
Learning Objectives
- Identify the order of a differential equation.
- Explain what is meant by a solution to a differential equation.
- Distinguish between the general solution and a particular solution of a differential equation.
- Identify an initial-value problem.
- Identify whether a given function is a solution to a differential equation or an initial-value problem.
Calculus is the mathematics of change, and rates of change are expressed by derivatives. Thus, one of the most common ways to use calculus is to set up an equation containing an unknown function \(y=f(x)\) and its derivative, known as a differential equation. Solving such equations often provides information about how quantities change and frequently provides insight into how and why the changes occur.
Techniques for solving differential equations can take many different forms, including direct solution, use of graphs, or computer calculations. We introduce the main ideas in this chapter and describe them in a little more detail later in the course. In this section we study what differential equations are, how to verify their solutions, some methods that are used for solving them, and some examples of common and useful equations.
General Differential Equations
Consider the equation \(y′=3x^2,\) which is an example of a differential equation because it includes a derivative. There is a relationship between the variables \(x\) and \(y:y\) is an unknown function of \(x\). Furthermore, the left-hand side of the equation is the derivative of \(y\). Therefore we can interpret this equation as follows: Start with some function \(y=f(x)\) and take its derivative. The answer must be equal to \(3x^2\). What function has a derivative that is equal to \(3x^2\)? One such function is \(y=x^3\), so this function is considered a solution to a differential equation.
Definition: differential equation
A differential equation is an equation involving an unknown function \(y=f(x)\) and one or more of its derivatives. A solution to a differential equation is a function \(y=f(x)\) that satisfies the differential equation when \(f\) and its derivatives are substituted into the equation.
Go to this website to explore more on this topic.
Some examples of differential equations and their solutions appear in Table \(\PageIndex{1}\).
| Equation | Solution |
|---|---|
| \(y'=2x\) | \(y=x^2\) |
| \(y'+3y=6x+11\) | \(y=e^{−3x}+2x+3\) |
| \(y''−3y'+2y=24e^{−2x}\) | \(y=3e^x−4e^{2x}+2e^{−2x}\) |
Note that a solution to a differential equation is not necessarily unique, primarily because the derivative of a constant is zero. For example, \(y=x^2+4\) is also a solution to the first differential equation in Table \(\PageIndex{1}\). We will return to this idea a little bit later in this section. For now, let’s focus on what it means for a function to be a solution to a differential equation.
Example \(\PageIndex{1}\): Verifying Solutions of Differential Equations
Verify that the function \(y=e^{−3x}+2x+3\) is a solution to the differential equation \(y′+3y=6x+11\).
Solution
To verify the solution, we first calculate \(y′\) using the chain rule for derivatives. This gives \(y′=−3e^{−3x}+2\). Next we substitute \(y\) and \(y′\) into the left-hand side of the differential equation:
\((−3e^{−2x}+2)+3(e^{−2x}+2x+3).\)
The resulting expression can be simplified by first distributing to eliminate the parentheses, giving
\(−3e^{−2x}+2+3e^{−2x}+6x+9.\)
Combining like terms leads to the expression \(6x+11\), which is equal to the right-hand side of the differential equation. This result verifies that \(y=e^{−3x}+2x+3\) is a solution of the differential equation.
Exercise \(\PageIndex{1}\)
Verify that \(y=2e^{3x}−2x−2\) is a solution to the differential equation \(y′−3y=6x+4.\)
- Hint
-
First calculate \(y′\) then substitute both \(y′\) and \(y\) into the left-hand side.
It is convenient to define characteristics of differential equations that make it easier to talk about them and categorize them. The most basic characteristic of a differential equation is its order.
Definition: order of a differential equation
The order of a differential equation is the highest order of any derivative of the unknown function that appears in the equation.
Example \(\PageIndex{2}\): Identifying the Order of a Differential Equation
The highest derivative in the equation is \(y′\),
What is the order of each of the following differential equations?
- \(y′−4y=x^2−3x+4\)
- \(x^2y'''−3xy''+xy′−3y=\sin x\)
- \(\frac{4}{x}y^{(4)}−\frac{6}{x^2}y''+\frac{12}{x^4}y=x^3−3x^2+4x−12\)
Solution
- The highest derivative in the equation is \(y′\),so the order is \(1\).
- The highest derivative in the equation is \(y'''\), so the order is \(3\).
- The highest derivative in the equation is \(y^{(4)}\), so the order is \(4\).
Exercise \(\PageIndex{2}\)
What is the order of the following differential equation?
\((x^4−3x)y^{(5)}−(3x^2+1)y′+3y=\sin x\cos x\)
- Hint
-
What is the highest derivative in the equation?
- Answer
-
\(5\)
General and Particular Solutions
We already noted that the differential equation \(y′=2x\) has at least two solutions: \(y=x^2\) and \(y=x^2+4\). The only difference between these two solutions is the last term, which is a constant. What if the last term is a different constant? Will this expression still be a solution to the differential equation? In fact, any function of the form \(y=x^2+C\), where \(C\) represents any constant, is a solution as well. The reason is that the derivative of \(x^2+C\) is \(2x\), regardless of the value of \(C\). It can be shown that any solution of this differential equation must be of the form \(y=x^2+C\). This is an example of a general solution to a differential equation. A graph of some of these solutions is given in Figure \(\PageIndex{1}\). (Note: in this graph we used even integer values for C ranging between \(−4\) and \(4\). In fact, there is no restriction on the value of \(C\); it can be an integer or not.)
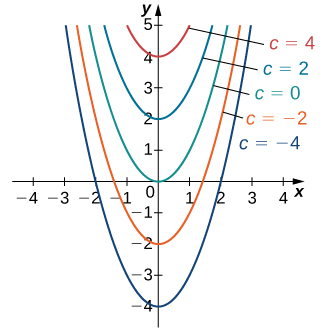
In this example, we are free to choose any solution we wish; for example, \(y=x^2−3\) is a member of the family of solutions to this differential equation. This is called a particular solution to the differential equation. A particular solution can often be uniquely identified if we are given additional information about the problem.
Example \(\PageIndex{3}\): Finding a Particular Solution
Find the particular solution to the differential equation \(y′=2x\) passing through the point \((2,7)\).
Solution
Any function of the form \(y=x^2+C\) is a solution to this differential equation. To determine the value of \(C\), we substitute the values \(x=2\) and \(y=7\) into this equation and solve for \(C\):
\[ \begin{align*} y =x^2+C \\[4pt] 7 =2^2+C \\[4pt] =4+C \\[4pt] C =3. \end{align*}\]
Therefore the particular solution passing through the point \((2,7)\) is \(y=x^2+3\).
Exercise \(\PageIndex{3}\)
Find the particular solution to the differential equation
\[ y′=4x+3 \nonumber\]
passing through the point \((1,7),\) given that \(y=2x^2+3x+C\) is a general solution to the differential equation.
- Hint
-
First substitute \(x=1\) and \(y=7\) into the equation, then solve for \(C\).
- Answer
-
\[ y=2x^2+3x+2 \nonumber\]
Initial-Value Problems
Usually a given differential equation has an infinite number of solutions, so it is natural to ask which one we want to use. To choose one solution, more information is needed. Some specific information that can be useful is an initial value, which is an ordered pair that is used to find a particular solution.
A differential equation together with one or more initial values is called an initial-value problem. The general rule is that the number of initial values needed for an initial-value problem is equal to the order of the differential equation. For example, if we have the differential equation \(y′=2x\), then \(y(3)=7\) is an initial value, and when taken together, these equations form an initial-value problem. The differential equation \(y''−3y′+2y=4e^x\) is second order, so we need two initial values. With initial-value problems of order greater than one, the same value should be used for the independent variable. An example of initial values for this second-order equation would be \(y(0)=2\) and \(y′(0)=−1.\) These two initial values together with the differential equation form an initial-value problem. These problems are so named because often the independent variable in the unknown function is \(t\), which represents time. Thus, a value of \(t=0\) represents the beginning of the problem.
Example \(\PageIndex{4}\): Verifying a Solution to an Initial-Value Problem
Verify that the function \(y=2e^{−2t}+e^t\) is a solution to the initial-value problem
\[ y′+2y=3e^t, \quad y(0)=3.\nonumber\]
Solution
For a function to satisfy an initial-value problem, it must satisfy both the differential equation and the initial condition. To show that \(y\) satisfies the differential equation, we start by calculating \(y′\). This gives \(y′=−4e^{−2t}+e^t\). Next we substitute both \(y\) and \(y′\) into the left-hand side of the differential equation and simplify:
\[ \begin{align*} y′+2y &=(−4e^{−2t}+e^t)+2(2e^{−2t}+e^t) \\[4pt] &=−4e^{−2t}+e^t+4e^{−2t}+2e^t =3e^t. \end{align*}\]
This is equal to the right-hand side of the differential equation, so \(y=2e^{−2t}+e^t\) solves the differential equation. Next we calculate \(y(0)\):
\[ y(0)=2e^{−2(0)}+e^0=2+1=3. \nonumber\]
This result verifies the initial value. Therefore the given function satisfies the initial-value problem.
Exercise \(\PageIndex{4}\)
Verify that \(y=3e^{2t}+4\sin t\) is a solution to the initial-value problem
\[ y′−2y=4\cos t−8\sin t,y(0)=3. \nonumber\]
- Hint
-
First verify that \(y\) solves the differential equation. Then check the initial value.
In Example \(\PageIndex{4}\), the initial-value problem consisted of two parts. The first part was the differential equation \(y′+2y=3e^x\), and the second part was the initial value \(y(0)=3.\) These two equations together formed the initial-value problem.
The same is true in general. An initial-value problem will consists of two parts: the differential equation and the initial condition. The differential equation has a family of solutions, and the initial condition determines the value of \(C\). The family of solutions to the differential equation in Example \(\PageIndex{4}\) is given by \(y=2e^{−2t}+Ce^t.\) This family of solutions is shown in Figure \(\PageIndex{2}\), with the particular solution \(y=2e^{−2t}+e^t\) labeled.
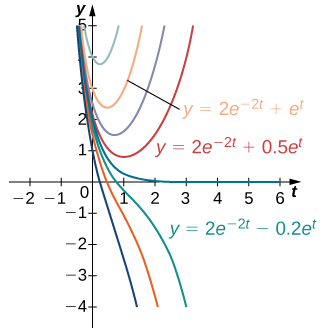
Example \(\PageIndex{5}\): Solving an Initial-value Problem
Solve the following initial-value problem:
\[ y′=3e^x+x^2−4,y(0)=5. \nonumber\]
Solution
The first step in solving this initial-value problem is to find a general family of solutions. To do this, we find an antiderivative of both sides of the differential equation
\[∫y′\,dx=∫(3e^x+x^2−4)\,dx, \nonumber\]
namely,
\(y+C_1=3e^x+\frac{1}{3}x^3−4x+C_2\).
We are able to integrate both sides because the y term appears by itself. Notice that there are two integration constants: \(C_1\) and \(C_2\). Solving this equation for \(y\) gives
\(y=3e^x+\frac{1}{3}x^3−4x+C_2−C_1.\)
Because \(C_1\) and \(C_2\) are both constants, \(C_2−C_1\) is also a constant. We can therefore define \(C=C_2−C_1,\) which leads to the equation
\(y=3e^x+\frac{1}{3}x^3−4x+C.\)
Next we determine the value of \(C\). To do this, we substitute \(x=0\) and \(y=5\) into this equation and solve for \(C\):
\[ \begin{align*} 5 &=3e^0+\frac{1}{3}0^3−4(0)+C \\[4pt] 5 &=3+C \\[4pt] C&=2 \end{align*}.\]
Now we substitute the value \(C=2\) into the general equation. The solution to the initial-value problem is \(y=3e^x+\frac{1}{3}x^3−4x+2.\)
Analysis
The difference between a general solution and a particular solution is that a general solution involves a family of functions, either explicitly or implicitly defined, of the independent variable. The initial value or values determine which particular solution in the family of solutions satisfies the desired conditions.
Exercise \(\PageIndex{5}\)
Solve the initial-value problem
\[ y′=x^2−4x+3−6e^x,y(0)=8. \nonumber \]
- Hint
-
First take the antiderivative of both sides of the differential equation. Then substitute \(x=0\) and \(y=8\) into the resulting equation and solve for \(C\).
- Answer
-
\(y=\frac{1}{3}x^3−2x^2+3x−6e^x+14\)
In physics and engineering applications, we often consider the forces acting upon an object, and use this information to understand the resulting motion that may occur. For example, if we start with an object at Earth’s surface, the primary force acting upon that object is gravity. Physicists and engineers can use this information, along with Newton’s second law of motion (in equation form \(F=ma\), where \(F\) represents force, \(m\) represents mass, and \(a\) represents acceleration), to derive an equation that can be solved.
In Figure \(\PageIndex{3}\) we assume that the only force acting on a baseball is the force of gravity. This assumption ignores air resistance. (The force due to air resistance is considered in a later discussion.) The acceleration due to gravity at Earth’s surface, g, is approximately \(9.8\,\text{m/s}^2\). We introduce a frame of reference, where Earth’s surface is at a height of 0 meters. Let \(v(t)\) represent the velocity of the object in meters per second. If \(v(t)>0\), the ball is rising, and if \(v(t)<0\), the ball is falling (Figure).
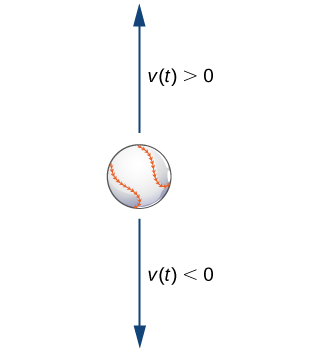
Our goal is to solve for the velocity \(v(t)\) at any time \(t\). To do this, we set up an initial-value problem. Suppose the mass of the ball is \(m\), where \(m\) is measured in kilograms. We use Newton’s second law, which states that the force acting on an object is equal to its mass times its acceleration \((F=ma)\). Acceleration is the derivative of velocity, so \(a(t)=v′(t)\). Therefore the force acting on the baseball is given by \(F=mv′(t)\). However, this force must be equal to the force of gravity acting on the object, which (again using Newton’s second law) is given by \(F_g=−mg\), since this force acts in a downward direction. Therefore we obtain the equation \(F=F_g\), which becomes \(mv′(t)=−mg\). Dividing both sides of the equation by \(m\) gives the equation
\[ v′(t)=−g.\]
Notice that this differential equation remains the same regardless of the mass of the object.
We now need an initial value. Because we are solving for velocity, it makes sense in the context of the problem to assume that we know the initial velocity, or the velocity at time \(t=0.\) This is denoted by \(v(0)=v_0.\)
Example \(\PageIndex{6}\): Velocity of a Moving Baseball
A baseball is thrown upward from a height of \(3\) meters above Earth’s surface with an initial velocity of \(10\) m/s, and the only force acting on it is gravity. The ball has a mass of \(0.15\) kg at Earth’s surface.
- Find the velocity \(v(t)\) of the basevall at time \(t\).
- What is its velocity after \(2\) seconds?
Solution
a. From the preceding discussion, the differential equation that applies in this situation is
\(v′(t)=−g,\)
where \(g=9.8\, \text{m/s}^2\). The initial condition is \(v(0)=v_0\), where \(v_0=10\) m/s. Therefore the initial-value problem is \(v′(t)=−9.8\,\text{m/s}^2,\,v(0)=10\) m/s.
The first step in solving this initial-value problem is to take the antiderivative of both sides of the differential equation. This gives
\[\int v′(t)\,dt=∫−9.8\,dt \nonumber \]
\(v(t)=−9.8t+C.\)
The next step is to solve for \(C\). To do this, substitute \(t=0\) and \(v(0)=10\):
\[ \begin{align*} v(t) &=−9.8t+C \\[4pt] v(0) &=−9.8(0)+C \\[4pt] 10 &=C. \end{align*}\]
Therefore \(C=10\) and the velocity function is given by \(v(t)=−9.8t+10.\)
b. To find the velocity after \(2\) seconds, substitute \(t=2\) into \(v(t)\).
\[ \begin{align*} v(t)&=−9.8t+10 \\[4pt] v(2)&=−9.8(2)+10 \\[4pt] v(2) &=−9.6\end{align*}\]
The units of velocity are meters per second. Since the answer is negative, the object is falling at a speed of \(9.6\) m/s.
Exercise \(\PageIndex{6}\)
Suppose a rock falls from rest from a height of \(100\) meters and the only force acting on it is gravity. Find an equation for the velocity \(v(t)\) as a function of time, measured in meters per second.
- Hint
-
What is the initial velocity of the rock? Use this with the differential equation in Example \(\PageIndex{6}\) to form an initial-value problem, then solve for \(v(t)\).
- Answer
-
\(v(t)=−9.8t\)
A natural question to ask after solving this type of problem is how high the object will be above Earth’s surface at a given point in time. Let \(s(t)\) denote the height above Earth’s surface of the object, measured in meters. Because velocity is the derivative of position (in this case height), this assumption gives the equation \(s′(t)=v(t)\). An initial value is necessary; in this case the initial height of the object works well. Let the initial height be given by the equation \(s(0)=s_0\). Together these assumptions give the initial-value problem
\[ s′(t)=v(t),s(0)=s_0.\]
If the velocity function is known, then it is possible to solve for the position function as well.
Example \(\PageIndex{7}\): Height of a Moving Baseball
A baseball is thrown upward from a height of \(3\) meters above Earth’s surface with an initial velocity of \(10m/s\), and the only force acting on it is gravity. The ball has a mass of \(0.15\) kilogram at Earth’s surface.
- Find the position \(s(t)\) of the baseball at time \(t\).
- What is its height after \(2\) seconds?
Solution
We already know the velocity function for this problem is \(v(t)=−9.8t+10\). The initial height of the baseball is \(3\) meters, so \(s_0=3\). Therefore the initial-value problem for this example is
To solve the initial-value problem, we first find the antiderivatives:
\[∫s′(t)\,dt=∫(−9.8t+10)\,dt \nonumber \]
\(s(t)=−4.9t^2+10t+C.\)
Next we substitute \(t=0\) and solve for \(C\):
\(s(t)=−4.9t^2+10t+C\)
\(s(0)=−4.9(0)^2+10(0)+C\)
\(3=C\).
Therefore the position function is \(s(t)=−4.9t^2+10t+3.\)
b. The height of the baseball after \(2\) sec is given by \(s(2):\)
\(s(2)=−4.9(2)^2+10(2)+3=−4.9(4)+23=3.4.\)
Therefore the baseball is \(3.4\) meters above Earth’s surface after \(2\) seconds. It is worth noting that the mass of the ball cancelled out completely in the process of solving the problem.
Key Concepts
- A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. A solution is a function \(y=f(x)\) that satisfies the differential equation when \(f\) and its derivatives are substituted into the equation.
- The order of a differential equation is the highest order of any derivative of the unknown function that appears in the equation.
- A differential equation coupled with an initial value is called an initial-value problem. To solve an initial-value problem, first find the general solution to the differential equation, then determine the value of the constant. Initial-value problems have many applications in science and engineering.
Glossary
- differential equation
- an equation involving a function \(y=y(x)\) and one or more of its derivatives
- general solution (or family of solutions)
- the entire set of solutions to a given differential equation
- initial value(s)
- a value or set of values that a solution of a differential equation satisfies for a fixed value of the independent variable
- initial velocity
- the velocity at time \(t=0\)
- initial-value problem
- a differential equation together with an initial value or values
- order of a differential equation
- the highest order of any derivative of the unknown function that appears in the equation
- particular solution
- member of a family of solutions to a differential equation that satisfies a particular initial condition
- solution to a differential equation
- a function \(y=f(x)\) that satisfies a given differential equation
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


