5.7E: Excersies

Last updated
Save as PDF

Page ID: 25934

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercise $\PageIndex{1}$

Use the following figure as an aid in identifying the relationship between the rectangular, cylindrical, and spherical coordinate systems.

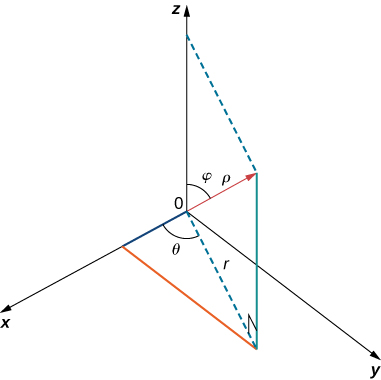
$This figure is the first octant of the 3-dimensional coordinate system. There is a line segment from the origin upwards. It is labeled “rho.” The angle between this line segment and the z-axis is labeled “phi.” There is also a broken line from the origin to the shadow of the point. This line segment is in the x y-plane and is labeled “r.” The angle between r and the x-axis is labeled “theta.”$

For the following exercises, the cylindrical coordinates $\displaystyle (r,θ,z)$ of a point are given. Find the rectangular coordinates $\displaystyle (x,y,z)$ of the point.

1) $\displaystyle (4,\frac{π}{6},3)$

Answer: $\displaystyle (2\sqrt{3},2,3)$

2) $\displaystyle (3,\frac{π}{3},5)$

3) $\displaystyle (4,\frac{7π}{6},3)$

Answer: $\displaystyle −2\sqrt{3},−2,3)$

4) $\displaystyle (2,π,−4)$

For the following exercises, the rectangular coordinates $\displaystyle (x,y,z)$ of a point are given. Find the cylindrical coordinates $\displaystyle (r,θ,z)$of the point.

5) $\displaystyle (1,\sqrt{3},2)$

Answer: $\displaystyle (2,\frac{π}{3},2)$

6) $\displaystyle (1,1,5)$

7) $\displaystyle (3,−3,7)$

Answer: $\displaystyle (3\sqrt{2},−\frac{π}{4},7)$

8) $\displaystyle (−2\sqrt{2},2\sqrt{2},4)$

Exercise $\PageIndex{2}$

For the following exercises, the equation of a surface in cylindrical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

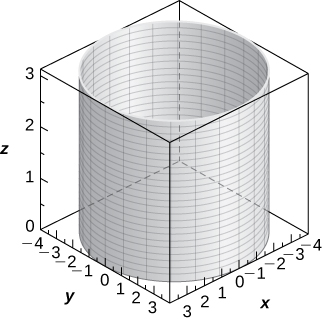
9) [T] $\displaystyle r=4$

Answer

A cylinder of equation $\displaystyle x^2+y^2=16,$ with its center at the origin and rulings parallel to the z-axis,

$This figure is a right circular cylinder, vertical. It is inside of a box. The edges of the box represent the x, y, and z axes.$

10) [T] $\displaystyle z=r^2cos^2θ$

11) [T] $\displaystyle r^2cos(2θ)+z^2+1=0$

Answer

Hyperboloid of two sheets of equation $\displaystyle −x^2+y^2−z^2=1,$ with the y-axis as the axis of symmetry,

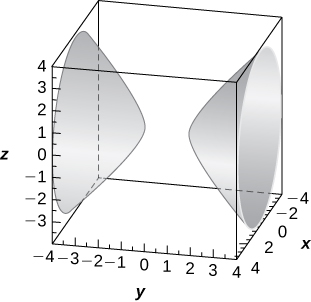
$This figure is a elliptic cone surface that is horizontal. It is inside of a box. The edges of the box represent the x, y, and z axes.$

12) [T] $\displaystyle r=3sinθ$

13) [T] $\displaystyle r=2cosθ$

Answer

Cylinder of equation $\displaystyle x^2−2x+y^2=0,$ with a center at $\displaystyle (1,0,0)$ and radius $\displaystyle 1$, with rulings parallel to the z-axis,

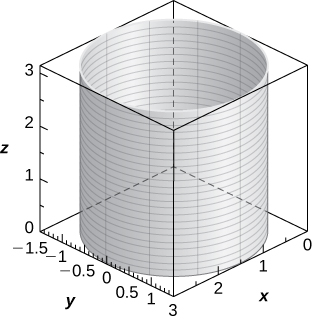
$This figure is a right circular cylinder, vertical. It is inside of a box. The edges of the box represent the x, y, and z axes.$

14) [T] $\displaystyle r^2+z^2=5$

15) [T] $\displaystyle r=2secθ$

Answer

Plane of equation $\displaystyle x=2,$

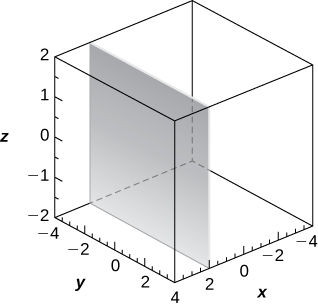
$This figure is a vertical parallelogram where x = 2 and parallel to the y z-plane. It is inside of a box. The edges of the box represent the x, y, and z axes.$

16) [T] $\displaystyle r=3cscθ$

Exercise $\PageIndex{3}$

For the following exercises, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in cylindrical coordinates.

17) $\displaystyle z=3$

Answer: $\displaystyle z=3$

18) $\displaystyle x=6$

19) $\displaystyle x^2+y^2+z^2=9$

Answer: $\displaystyle r^2+z^2=9$

20) $\displaystyle y=2x^2$

21) $\displaystyle x^2+y^2−16x=0$

Answer: $\displaystyle r=16cosθ,r=0$

22) $\displaystyle x^2+y^2−3\sqrt{x^2+y^2}+2=0$

Exercise $\PageIndex{4}$

For the following exercises, the spherical coordinates $\displaystyle (ρ,θ,φ)$ of a point are given. Find the rectangular coordinates $\displaystyle (x,y,z)$ of the point.

23) $\displaystyle (3,0,π)$

Answer: $\displaystyle (0,0,−3)$

24) $\displaystyle (1,\frac{π}{6},\frac{π}{6})$

25) $\displaystyle (12,−\frac{π}{4},\frac{π}{4})$

Answer: $\displaystyle (6,−6,\sqrt{2})$

26) $\displaystyle (3,\frac{π}{4},\frac{π}{6})$

Exercise $\PageIndex{5}$

For the following exercises, the rectangular coordinates $\displaystyle (x,y,z)$ of a point are given. Find the spherical coordinates $\displaystyle (ρ,θ,φ)$ of the point. Express the measure of the angles in degrees rounded to the nearest integer.

27) $\displaystyle (4,0,0)$

Answer: $\displaystyle (4,0,90°)$

28) $\displaystyle (−1,2,1)$

29) $\displaystyle (0,3,0)$

Answer: $\displaystyle (3,90°,90°)$

30) $\displaystyle (−2,2\sqrt{3},4)$

Exercise $\PageIndex{6}$

For the following exercises, the equation of a surface in spherical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

31) [T] $\displaystyle ρ=3$

Answer

Sphere of equation $\displaystyle x^2+y^2+z^2=9$ centered at the origin with radius $\displaystyle 3$,

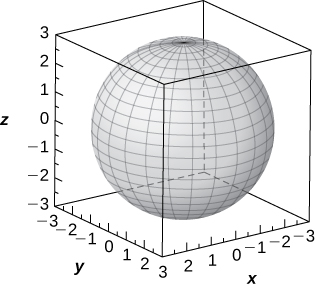
$This figure is a sphere. It is inside of a box. The edges of the box represent the x, y, and z axes.$

32) [T] $\displaystyle φ=\frac{π}{3}$

33) [T] $\displaystyle ρ=2cosφ$

Answer

Sphere of equation $\displaystyle x^2+y^2+(z−1)^2=1$ centered at $\displaystyle (0,0,1)$ with radius $\displaystyle 1$,

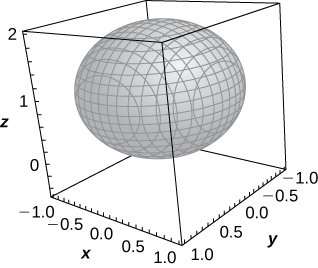
$This figure is a sphere of radius 1 centered in a box. The center of the sphere is the point (0, 0, 1).$

34) [T] $\displaystyle ρ=4cscφ$

35) [T] $\displaystyle φ=\frac{π}{2}$

Answer

The xy-plane of equation $\displaystyle z=0,$

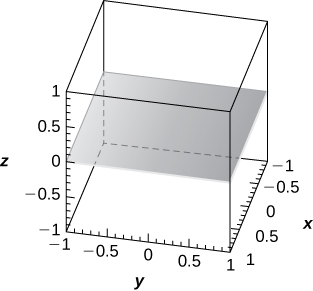
$This figure is a parallelogram representing a plane. It is parallel to the x y-plane at z = 0. It is inside of a box. The edges of the box represent the x, y, and z axes.$

36) [T] $\displaystyle ρ=6cscφsecθ$

Exercise $\PageIndex{7}$

For the following exercises, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in spherical coordinates. Identify the surface.

37) $\displaystyle x^2+y^2−3z^2=0, z≠0$

Answer: $\displaystyle φ=\frac{π}{3}$ or $\displaystyle φ=\frac{2π}{3};$ Elliptic cone

38) $\displaystyle x^2+y^2+z^2−4z=0$

39) $\displaystyle z=6$

Answer: $\displaystyle ρcosφ=6;$ Plane at $\displaystyle z=6$

40) $\displaystyle x^2+y^2=9$

Exercise $\PageIndex{8}$

For the following exercises, the cylindrical coordinates of a point are given. Find its associated spherical coordinates, with the measure of the angle φ

in radians rounded to four decimal places.

41) [T] $\displaystyle (1,\frac{π}{4},3)$

Answer: $\displaystyle (\sqrt{10},\frac{π}{4},0.3218)$

42) [T] $\displaystyle (5,π,12)$

43) $\displaystyle (3,\frac{π}{2},3)$

Answer: $\displaystyle (3\sqrt{2},\frac{π}{2},\frac{π}{4})$

44) $\displaystyle (3,−\frac{π}{6},3)$

Exercise $\PageIndex{9}$

For the following exercises, the spherical coordinates of a point are given. Find its associated cylindrical coordinates.

45) $\displaystyle (2,−\frac{π}{4},\frac{π}{2})$

Answer: $\displaystyle (2,−\frac{π}{4},0)$

46) $\displaystyle (4,\frac{π}{4},\frac{π}{6})$

47) $\displaystyle (8,\frac{π}{3},\frac{π}{2})$

Answer: $\displaystyle (8,\frac{π}{3},0)$

48) $\displaystyle (9,−\frac{π}{6},\frac{π}{3})$

Exercise $\PageIndex{10}$

For the following exercises, find the most suitable system of coordinates to describe the solids.

49) The solid situated in the first octant with a vertex at the origin and enclosed by a cube of edge length $\displaystyle a$, where $\displaystyle a>0$

Answer: Cartesian system, $\displaystyle {(x,y,z)|0≤x≤a,0≤y≤a,0≤z≤a}$

50) A spherical shell determined by the region between two concentric spheres centered at the origin, of radii of $\displaystyle a$ and $\displaystyle b$, respectively, where $\displaystyle b>a>0$

51) A solid inside sphere $\displaystyle x^2+y^2+z^2=9$ and outside cylinder $\displaystyle (x−\frac{3}{2})^2+y^2=\frac{9}{4}$

Answer: Cylindrical system, $\displaystyle {(r,θ,z)∣r^2+z^2≤9,r≥3cosθ,0≤θ≤2π}$

52) A cylindrical shell of height $\displaystyle 10$ determined by the region between two cylinders with the same center, parallel rulings, and radii of $\displaystyle 2$ and $\displaystyle 5$, respectively

Exercise $\PageIndex{11}$

53) [T] Use a CAS to graph in cylindrical coordinates the region between elliptic paraboloid $\displaystyle z=x^2+y^2$ and cone $\displaystyle x^2+y^2−z^2=0.$

Answer

The region is described by the set of points $\displaystyle {(r,θ,z)∣∣0≤r≤1,0≤θ≤2π,r^2≤z≤r}.$

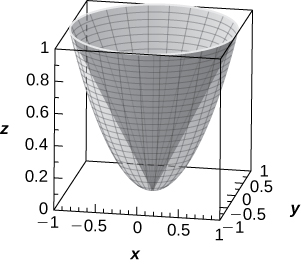
$This figure is a paraboloid, vertical. It is inside of a box. The edges of the box represent the x, y, and z axes.$

54) [T] Use a CAS to graph in spherical coordinates the “ice cream-cone region” situated above the xy-plane between sphere $\displaystyle x^2+y^2+z^2=4$ and elliptical cone $\displaystyle x^2+y^2−z^2=0.$

Exercise $\PageIndex{12}$

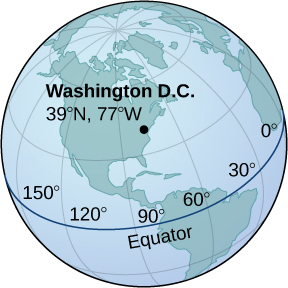
55) Washington, DC, is located at $\displaystyle 39°$ N and $\displaystyle 77°$ W (see the following figure). Assume the radius of Earth is $\displaystyle 4000$ mi. Express the location of Washington, DC, in spherical coordinates.

$This figure is an image of a globe. On the globe there is a point labeled where Washington, DC is located. It is labeled with 39 degrees north latitude and 77 degrees west longitude.$

Answer: $\displaystyle (4000,−77°,51°)$

56) San Francisco is located at $\displaystyle 37.78°N$ and $\displaystyle 122.42°W.$ Assume the radius of Earth is $\displaystyle 4000$mi. Express the location of San Francisco in spherical coordinates.

57) Find the latitude and longitude of Rio de Janeiro if its spherical coordinates are $\displaystyle (4000,−43.17°,102.91°).$

Answer: $\displaystyle 43.17°W, 22.91°S$

58) Find the latitude and longitude of Berlin if its spherical coordinates are $\displaystyle (4000,13.38°,37.48°).$

Exercise $\PageIndex{13}$

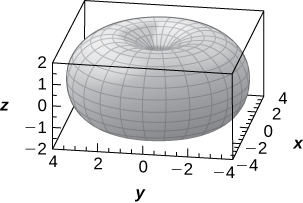
59) [T] Consider the torus of equation $\displaystyle (x^2+y^2+z^2+R^2−r^2)^2=4R^2(x^2+y^2),$ where $\displaystyle R≥r>0.$

a. Write the equation of the torus in spherical coordinates.

b. If $\displaystyle R=r,$ the surface is called a horn torus. Show that the equation of a horn torus in spherical coordinates is $\displaystyle ρ=2Rsinφ.$

c. Use a CAS to graph the horn torus with $\displaystyle R=r=2$ in spherical coordinates.

Answer

$\displaystyle a. ρ=0, ρ+R2−r2−2Rsinφ=0;$

$This figure is a torus. It is inside of a box. The edges of the box represent the x, y, and z axes.$

60) [T] The “bumpy sphere” with an equation in spherical coordinates is $\displaystyle ρ=a+bcos(mθ)sin(nφ)$, with $\displaystyle θ∈[0,2π]$ and $\displaystyle φ∈[0,π]$, where $\displaystyle a$ and $\displaystyle b$ are positive numbers and $\displaystyle m$ and $\displaystyle n$ are positive integers, may be used in applied mathematics to model tumor growth.

a. Show that the “bumpy sphere” is contained inside a sphere of equation $\displaystyle ρ=a+b.$ Find the values of $\displaystyle θ$ and $\displaystyle φ$ at which the two surfaces intersect.

b. Use a CAS to graph the surface for $\displaystyle a=14, b=2, m=4,$ and $\displaystyle n=6$ along with sphere $\displaystyle ρ=a+b.$

c. Find the equation of the intersection curve of the surface at b. with the cone $\displaystyle φ=\frac{π}{12}$. Graph the intersection curve in the plane of intersection.

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)