6.1E: Exercises

Exercise \(\PageIndex{1}\) functional value

For the following exercises, evaluate each function at the indicated values.

1) \(\displaystyle W(x,y)=4x^2+y^2.\) Find \(\displaystyle W(2,−1), W(−3,6).\)

Answer

Solution:\(\displaystyle 17,72\)

2) \(\displaystyle W(x,y)=4x^2+y^2\). Find \(\displaystyle W(2+h,3+h).\)

3) The volume of a right circular cylinder is calculated by a function of two variables, \(\displaystyle V(x,y)=πx^2y,\) where \(\displaystyle x\) is the radius of the right circular cylinder and \(\displaystyle y\) represents the height of the cylinder. Evaluate \(\displaystyle V(2,5)\) and explain what this means.

Answer

Solution:\(\displaystyle 20π.\) This is the volume when the radius is \(\displaystyle 2\) and the height is \(\displaystyle 5\).

4) An oxygen tank is constructed of a right cylinder of height \(\displaystyle y\) and radius \(\displaystyle x\) with two hemispheres of radius \(\displaystyle x\) mounted on the top and bottom of the cylinder. Express the volume of the cylinder as a function of two variables, \(\displaystyle x\) and \(\displaystyle y\), find \(\displaystyle V(10,2)\), and explain what this means.

Exercise \(\PageIndex{2}\) Domain

For the following exercises, find the domain of the function.

1) \(\displaystyle V(x,y)=4x^2+y^2\)

Answer

Solution:All points in the \(\displaystyle xy-plane\)

2) \(\displaystyle f(x,y)=\sqrt{x^2+y^2−4}\)

3) \(\displaystyle f(x,y)=4ln(y^2−x)\)

Answer

Solution:\(\displaystyle x<y^2\)

4) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)

5) \(\displaystyle z(x,y)=y^2−x^2\)

Answer

Solution:All real ordered pairs in the \(\displaystyle xy-plane\) of the form \(\displaystyle (a,b)\)

6) \(\displaystyle f(x,y)=\frac{y+2}{x^2}\)

Exercise \(\PageIndex{3}\) range

Find the range of the functions.

1) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)

Answer

Solution:\(\displaystyle \{z|0≤z≤4 \}\)

2) \(\displaystyle V(x,y)=4x^2+y^2\)

3) \(\displaystyle z=y^2−x^2\)

Answer

Solution:The set \(\displaystyle R\).

Exercise \(\PageIndex{4}\) Level Curves

For the following exercises, find the level curves of each function at the indicated value of \(\displaystyle c\) to visualize the given function.

1) \(\displaystyle z(x,y)=y^2−x^2, c=1\)

2) \(\displaystyle z(x,y)=y^2−x^2, c=4\)

Answer

Solution:\(\displaystyle y^2−x^2=4,\) a hyperbola

3) \(\displaystyle g(x,y)=x^2+y^2;c=4,c=9\)

4) \(\displaystyle g(x,y)=4−x−y;c=0,4\)

Answer

Solution:\(\displaystyle 4=x+y,\) a line; \(\displaystyle x+y=0,\) line through the origin

5) \(\displaystyle h(x,y)=2x−y;c=0,−2,2\)

Answer

Solution:\(\displaystyle 2x−y=0,2x−y=−2,2x−y=2;\) three lines

6) \(\displaystyle f(x,y)=x^2−y;c=1,2\)

7) \(\displaystyle g(x,y)=\frac{x}{x+y};c=−1,0,2\)

Answer

Solution:\(\displaystyle \frac{x}{x+y}=−1,\frac{x}{x+y}=0,\frac{x}{x+y}=2\)

8) \(\displaystyle g(x,y)=x^3−y;c=−1,0,2\)

9) \(\displaystyle g(x,y)=e^{xy};c=\frac{1}{2},3\)

Answer

Solution:\(\displaystyle e^{xy}=\frac{1}{2},e^{xy}=3\)

10) \(\displaystyle f(x,y)=x^2;c=4,9\)

12) \(\displaystyle f(x,y)=xy−x;c=−2,0,2\)

Answer

Solution:\(\displaystyle xy−x=−2,xy−x=0,xy−x=2\)

13) \(\displaystyle h(x,y)=ln(x^2+y^2);c=−1,0,1\)

14) \(\displaystyle g(x,y)=ln(\frac{y}{x^2});c=−2,0,2\)

Answer

Solution:\(\displaystyle e^{−2}x^2=y,y=x^2,y=e^2x^2\)

15) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}, c=3\)

16) \(\displaystyle f(x,y)=\frac{y+2}{x^2}, c=\)any constant

Answer

Solution:The level curves are parabolas of the form \(\displaystyle y=cx^2−2.\)

Exercise \(\PageIndex{5}\) Vertical Traces

For the following exercises, find the vertical traces of the functions at the indicated values of \(\displaystyle x\) and \(\displaystyle y\), and plot the traces.

1) \(\displaystyle z=4−x−y;x=2\)

2) \(\displaystyle f(x,y)=3x+y^3,x=1\)

Answer

Solution:\(\displaystyle z=3+y^3,\) a curve in the zy-plane with rulings parallel to the \(\displaystyle x-axis\)

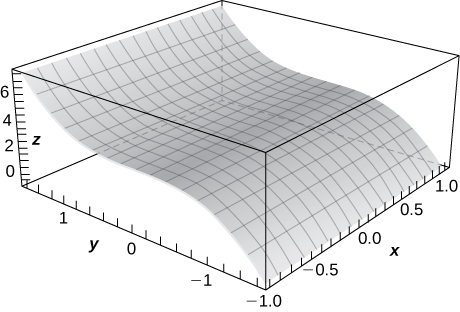
3) \(\displaystyle z=cos\sqrt{x^2+y^2} x=1\)

Exercise \(\PageIndex{6}\) Domain

Find the domain of the following functions.

1) \(\displaystyle z=\sqrt{100−4x^2−25y^2}\)

Answer

Solution:\(\displaystyle \frac{x^2}{25}+\frac{y^2}{4}≤1\)

2) \(\displaystyle z=ln(x−y^2)\)

3) \(\displaystyle f(x,y,z)=\frac{1}{\sqrt{36−4x^2−9y^2−z^2}}\)

Answer

Solution:\(\displaystyle \frac{x^2}{9}+\frac{y^2}{4}+\frac{z^2}{36}<1\)

4) \(\displaystyle f(x,y,z)=\sqrt{49−x^2−y^2−z^2}\)

5) \(\displaystyle f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}\)

Answer

Solution:All points in \(\displaystyle xyz-space\)

6) \(\displaystyle f(x,y)=cos\sqrt{x^2+y^2}\)

Exercise \(\PageIndex{7}\) Graph

For the following exercises, plot a graph of the function.

1) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}\)

Answer

Solution:

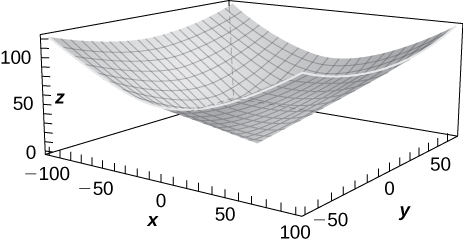
2) \(\displaystyle z=x^2+y^2\)

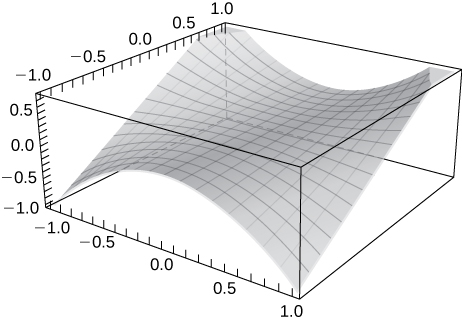
3) Use technology to graph \(\displaystyle z=x^2y.\)

Answer

Solution:

Exercise \(\PageIndex{8}\) Level curves

Sketch the following by finding the level curves. Verify the graph using technology.

1) \(\displaystyle f(x,y)=\sqrt{4−x^2−y^2}\)

2) \(\displaystyle f(x,y)=2−\sqrt{x^2+y^2}\)

Answer

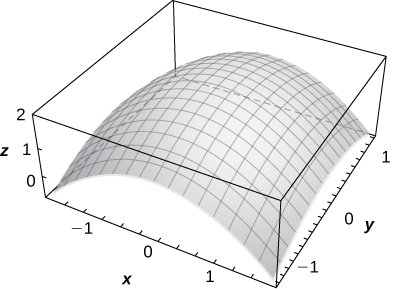
3) \(\displaystyle z=1+e^{−x^2−y^2}\)

4) \(\displaystyle z=cos\sqrt{x^2+y^2}\)

Answer

Solution:

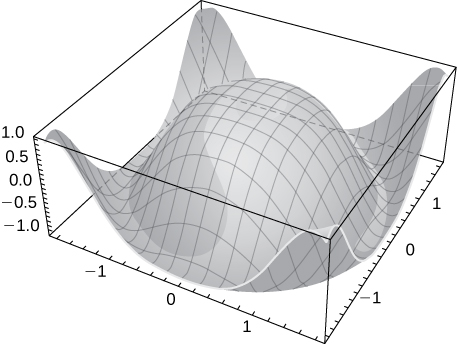
5) \(\displaystyle z=y^2−x^2\)

Exercise \(\PageIndex{9}\) Contour lines

1) Describe the contour lines for several values of \(\displaystyle c\) for \(\displaystyle z=x^2+y^2−2x−2y.\)

Answer

Solution:The contour lines are circles.

Exercise \(\PageIndex{10}\) level surface

Find the level surface for the functions of three variables and describe it.

1) \(\displaystyle w(x,y,z)=x−2y+z,c=4\)

2) \(\displaystyle w(x,y,z)=x^2+y^2+z^2,c=9\)

Answer

Solution:\(\displaystyle x^2+y^2+z^2=9\), a sphere of radius \(\displaystyle 3\)

3) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=−4\)

4) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=4\)

Answer

Solution:\(\displaystyle x^2+y^2−z^2=4,\) a hyperboloid of one sheet

5) \(\displaystyle w(x,y,z)=9x^2−4y^2+36z^2,c=0\)

Exercise \(\PageIndex{11}\) level curve at a given point

For the following exercises, find an equation of the level curve of \(\displaystyle f\) that contains the point \(\displaystyle P\).

1) \(\displaystyle f(x,y)=1−4x^2−y^2,P(0,1)\)

Answer

Solution:\(\displaystyle 4x^2+y^2=1,\)

2) \(\displaystyle g(x,y)=y^2arctanx,P(1,2)\)

3) \(\displaystyle g(x,y)=e^{xy}(x^2+y^2),P(1,0)\)

Answer

Solution:\(\displaystyle 1=e^{xy}(x^2+y^2)\)

Exercise \(\PageIndex{12}\) Applications

1) The strength \(\displaystyle E\) of an electric field at point \(\displaystyle (x,y,z)\) resulting from an infinitely long charged wire lying along the \(\displaystyle y-axis\) is given by \(\displaystyle E(x,y,z)=k/\sqrt{x^2+y^2}\), where \(\displaystyle k\) is a positive constant. For simplicity, let \(\displaystyle k=1\) and find the equations of the level surfaces for \(\displaystyle E=10\) and \(\displaystyle E=100.\)

2) A thin plate made of iron is located in the \(\displaystyle xy-plane.\) The temperature \(\displaystyle T\) in degrees Celsius at a point \(\displaystyle P(x,y)\) is inversely proportional to the square of its distance from the origin. Express \(\displaystyle T\) as a function of \(\displaystyle x\) and \(\displaystyle y\).

Answer

Solution:\(\displaystyle T(x,y)=\frac{k}{x^2+y^2}\)

3) Refer to the preceding problem. Using the temperature function found there, determine the proportionality constant if the temperature at point \(\displaystyle P(1,2)\) is \(\displaystyle 50°C.\) Use this constant to determine the temperature at point \(\displaystyle Q(3,4).\)

4) Refer to the preceding problem. Find the level curves for \(\displaystyle T=40°C\) and \(\displaystyle T=100°C,\) and describe what the level curves represent.

Answer

Solution:\(\displaystyle x^2+y^2=\frac{k}{40}, x^2+y^2=\frac{k}{100}\). The level curves represent circles of radii \(\displaystyle \sqrt{10k}/20\) and \(\displaystyle \sqrt{k}/10\)