4.2 E: Exercises
- Page ID
- 14723
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
Using sigma notation, write the following expressions as infinite series.
1) \(\displaystyle 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)
- Answer
-
Solution: \(\displaystyle \sum_{n=1}^∞\frac{1}{n}\)
2) \(\displaystyle 1−1+1−1+⋯\)
3) \(\displaystyle 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...\)
- Answer
-
Solution: \(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}\
4) \(\displaystyle sin1+sin1/2+sin1/3+sin1/4+⋯\)
Compute the first four partial sums \(\displaystyle S_1,…,S_4\) for the series having \(\displaystyle nth\) term \(\displaystyle a_n\) starting with \(\displaystyle n=1\) as follows.
5) \(\displaystyle a_n=n\)
- Answer
-
Solution: \(\displaystyle 1,3,6,10\)
6) \(\displaystyle a_n=1/n\)
7) \(\displaystyle a_n=sin(nπ/2)\)
- Answer
-
Solution: \(\displaystyle 1,1,0,0\)
8) \(\displaystyle a_n=(−1)^n\)
Exercise \(\PageIndex{2}\)
In the following exercises, compute the general term \(\displaystyle a_n\) of the series with the given partial sum \(\displaystyle S_n\). If the sequence of partial sums converges, find its limit \(\displaystyle S\).
1) \(\displaystyle S_n=1−\frac{1}{n}, n≥2\)
- Answer
-
Solution: \(\displaystyle a_n=S_n−S_{n−1}=\frac{1}{n−1}−\frac{1}{n}.\) Series converges to \(\displaystyle S=1.\)
2) \(\displaystyle S_n=\frac{n(n+1)}{2}, n≥1\)
3) \(\displaystyle S_n=\sqrt{n},n≥2\)
- Answer
-
Solution: \(\displaystyle a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\frac{1}{\sqrt{n−1}+\sqrt{n}}.\) Series diverges because partial sums are unbounded.
4) \(\displaystyle S_n=2−(n+2)/2^n,n≥1\)
Exercise \(\PageIndex{3}\)
For each of the following series, use the sequence of partial sums to determine whether the series converges or diverges.
1) \(\displaystyle \sum_{n=1}^∞\frac{n}{n+2}\)
- Answer
-
Solution: \(\displaystyle S_1=1/3, S_2=1/3+2/4>1/3+1/3=2/3, S_3=1/3+2/4+3/5>3⋅(1/3)=1.\) In general \(\displaystyle S_k>k/3.\) Series diverges
2) \(\displaystyle \sum_{n=1}^∞(1−(−1)^n))\)
3) \(\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}\) (Hint: Use a partial fraction decomposition like that for \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.)\)
- Answer
-
Solution:
\(\displaystyle S_1=1/(2.3)=1/6=2/3−1/2,\)
\(\displaystyle S_2=1/(2.3)+1/(3.4)=2/12+1/12=1/4=3/4−1/2,\)
\(\displaystyle S_3=1/(2.3)+1/(3.4)+1/(4.5)=10/60+5/60+3/60=3/10=4/5−1/2,\)
\(\displaystyle S_4=1/(2.3)+1/(3.4)+1/(4.5)+1/(5.6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.\)
The pattern is \(\displaystyle S_k=(k+1)/(k+2)−1/2\) and the series converges to \(\displaystyle 1/2.\)
4) \(\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}\) (Hint: Follow the reasoning for \(\displaystyle \sum_{n=1}^∞\frac{1}{n}.)\)
Exercise \(\PageIndex{4}\)
Suppose that \(\displaystyle \sum_{n=1}^∞a_n=1\), that \(\displaystyle \sum_{n=1}^∞b_n=−1\), that \(\displaystyle a_1=2\), and \(\displaystyle b_1=−3\). Find the sum of the indicated series.
1) \(\displaystyle \sum_{n=1}^∞(a_n+b_n)\)
- Answer
-
Solution: \(\displaystyle 0\)
2) \(\displaystyle \sum_{n=1}^∞(a_n−2b_n)\)
4) \(\displaystyle \sum_{n=2}^∞(a_n−b_n)\)
- Answer
-
Solution: \(\displaystyle −3\)
5) \(\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})\)
Exercise \(\PageIndex{5}\)
State whether the given series converges and explain why.
1) \(\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}\) (Hint: Rewrite using a change of index.)
- Answer
-
Solution: diverges, \(\displaystyle \sum_{n=1001}^∞\frac{1}{n}\)
2) \(\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}\) (Hint: Rewrite using a change of index.)
3) \(\displaystyle 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯\)
- Answer
-
Solution: convergent geometric series, \(\displaystyle r=1/10<1\)
4) \(\displaystyle 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯\)
5) \(\displaystyle 1+\frac{π}{e}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯\)
- Answer
-
Solution: convergent geometric series, \(\displaystyle r=π/e^2<1\)
6) \(\displaystyle 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯\)
Exercise \(\PageIndex{6}\)
For \(\displaystyle a_n\) as follows, write the sum as a geometric series of the form \(\displaystyle \sum_{n=1}^∞ar^n\). State whether the series converges and if it does, find the value of \(\displaystyle \sum a_n\).
1) \(\displaystyle a_1=−1\) and \(\displaystyle a_n/a_{n+1}=−5\) for \(\displaystyle n≥1.\)
- Answer
-
Solution: \(\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n\), converges to \(\displaystyle −5/6\)
2) \(\displaystyle a_1=2\) and \(\displaystyle a_n/a_{n+1}=1/2\) for \(\displaystyle n≥1.\)
3) \(\displaystyle a_1=10\) and \(\displaystyle a_n/a_{n+1}=10\) for \(\displaystyle n≥1\).
- Answer
-
Solution: \(\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,\) converges to \(\displaystyle 100/9\)
4) \(\displaystyle a_1=1/10\) and \(\displaystyle a_n/a_{n+1}=−10\) for \(\displaystyle n≥1\).
Exercise \(\PageIndex{7}\)
Use the identity \(\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n\) to express the function as a geometric series in the indicated term.
1) \(\displaystyle \frac{x}{1+x}\) in \(\displaystyle x\)
- Answer
-
Solution: \(\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n\
2) \(\displaystyle \frac{\sqrt{x}}{1−x^{3/2}}\) in \(\displaystyle \sqrt{x}\)
3) \(\displaystyle \frac{1}{1+sin^2x}\) in \(\displaystyle sinx\)
- Answer
-
Solution: \(\displaystyle \sum_{n=0}^∞(−1)^nsin^2n(x)\)
4) \(\displaystyle sec^2x\) in \(\displaystyle sinx\)
Exercise \(\PageIndex{8}\)
Evaluate the following telescoping series or state whether the series diverges.
1) \(\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}\)
- Answer
-
Solution: \(\displaystyle S_k=2−2^{1/(k+1)}→1\) as \(\displaystyle k→∞.\)
2) \(\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}\)
3) \(\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})\)
- Answer
-
Soution: \(\displaystyle S_k=1−\sqrt{k+1}\) diverges.
4) \(\displaystyle \sum_{n=1}^∞(sinn−sin(n+1))\)
Exercise \(\PageIndex{9}\)
Evaluate the following telescoping series or state whether the series diverges.
1) \(\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}\)
- Answer
-
Solution: \(\displaystyle S_k=2−2^{1/(k+1)}→1\) as \(\displaystyle k→∞.\)
2) \(\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}\)
3) \(\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})\)
- Answer
-
Soution: \(\displaystyle S_k=1−\sqrt{k+1}\) diverges.
4) \(\displaystyle \sum_{n=1}^∞(sinn−sin(n+1))\)
Exercise \(\PageIndex{10}\)
Express the following series as a telescoping sum and evaluate its nth partial sum.
1) \(\displaystyle \sum_{n=1}^∞ln(\frac{n}{n+1})\)
- Answer
-
Solution: \(\displaystyle \sum_{n=1}^∞lnn−ln(n+1),S_k=−ln(k+1)\)
2) \(\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}\) (Hint: Factor denominator and use partial fractions.)
3) \(\displaystyle \sum_{n=2}^∞\frac{ln(1+\frac{1}{n})}{lnnln(n+1)}\)
- Answer
-
Solution: \(\displaystyle a_n=\frac{1}{lnn}−\frac{1}{ln(n+1)}\) and \(\displaystyle S_k=\frac{1}{ln(2)}−\frac{1}{ln(k+1)}→\frac{1}{ln(2)}\)
4) \(\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}\) (Hint: Look at \(\displaystyle 1/(n2^n)\).
Exercise \(\PageIndex{11}\)
A general telescoping series is one in which all but the first few terms cancel out after summing a given number of successive terms.
1) Let \(\displaystyle a_n=f(n)−2f(n+1)+f(n+2),\) in which \(\displaystyle f(n)→0\) as \(\displaystyle n→∞.\) Find \(\displaystyle \sum_{n=1}^∞a_n\).
- Answer
-
Solution: \(\displaystyle sum_{n=1}^∞a_n=f(1)−f(2)\)
2) \(\displaystyle a_n=f(n)−f(n+1)−f(n+2)+f(n+3),\) in which \(\displaystyle f(n)→0\) as \(\displaystyle n→∞\). Find \(\displaystyle \sum_{n=1}^∞a_n\).
3)Suppose that \(\displaystyle a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),\) where \(\displaystyle f(n)→0\) as \(\displaystyle n→∞\). Find a condition on the coefficients \(\displaystyle c_0,…,c_4\) that make this a general telescoping series.
- Answer
-
Solution: \(\displaystyle c_0+c_1+c_2+c_3+c_4=0\)
4) Evaluate \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}\) (Hint: \(\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)})\)
5) Evaluate \(\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.\)
- Answer
-
Solution: \(\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1}, S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2\)
6) Find a formula for \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+N)}\) where \(\displaystyle N\) is a positive integer.
Exercise \(\PageIndex{12}\)
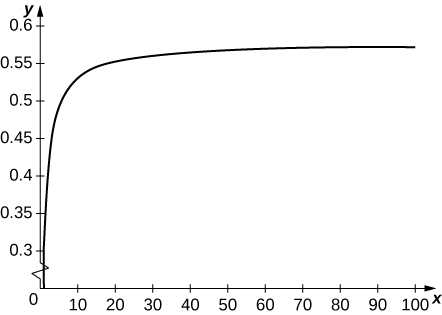
1) [T] Define a sequence \(\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−lnk\). Use the graph of \(\displaystyle 1/x\) to verify that \(\displaystyle t_k\) is increasing. Plot \(\displaystyle t_k\) for \(\displaystyle k=1…100\) and state whether it appears that the sequence converges.
- Answer
-
Solution: \(\displaystyle t_k\) converges to \(\displaystyle 0.57721…t_k\) is a sum of rectangles of height \(\displaystyle 1/k\) over the interval \(\displaystyle [k,k+1]\) which lie above the graph of \(\displaystyle 1/x\).
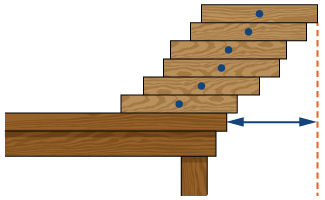
2) [T] Suppose that \(\displaystyle N\) equal uniform rectangular blocks are stacked one on top of the other, allowing for some overhang. Archimedes’ law of the lever implies that the stack of \(\displaystyle N\) blocks is stable as long as the center of mass of the top \(\displaystyle (N−1)\) blocks lies at the edge of the bottom block. Let \(\displaystyle x\) denote the position of the edge of the bottom block, and think of its position as relative to the center of the next-to-bottom block. This implies that \(\displaystyle (N−1)x=(\frac{1}{2}−x)\) or \(\displaystyle x=1/(2N)\). Use this expression to compute the maximum overhang (the position of the edge of the top block over the edge of the bottom block.) See the following figure.
Each of the following infinite series converges to the given multiple of \(\displaystyle π\) or \(\displaystyle 1/π\).
Exercise \(\PageIndex{13}\)
In each case, find the minimum value of \(\displaystyle N\) such that the \(\displaystyle Nth\) partial sum of the series accurately approximates the left-hand side to the given number of decimal places, and give the desired approximate value. Up to \(\displaystyle 15\) decimals place, \(\displaystyle π=3.141592653589793....\)
1) [T] \(\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},\) error \(\displaystyle <0.0001\)
- Answer
-
Solution: \(\displaystyle N=22, S_N=6.1415\)
2) [T] \(\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},\) error \(\displaystyle <10^{−4}\)
3) [T] \(\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},\) error \(\displaystyle <10^{−12}\)
- Answer
-
solution: \(\displaystyle N=3, S_N=1.559877597243667...\)
4) [T] \(\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}\), error \(\displaystyle <10^{−15}\)
Exercise \(\PageIndex{14}\)
1) [T] A fair coin is one that has probability \(\displaystyle 1/2\) of coming up heads when flipped.
a. What is the probability that a fair coin will come up tails \(\displaystyle n\) times in a row?
b. Find the probability that a coin comes up heads for the first time after an even number of coin flips.
- Answer
-
Solution: a. The probability of any given ordered sequence of outcomes for \(\displaystyle n\) coin flips is \(\displaystyle 1/2^n\). b. The probability of coming up heads for the first time on the \(\displaystyle n\) th flip is the probability of the sequence \(\displaystyle TT…TH\) which is \(\displaystyle 1/2^n\). The probability of coming up heads for the first time on an even flip is \(\displaystyle \sum_{n=1}^∞1/2^{2n}\) or \(\displaystyle 1/3\).
2) [T] Find the probability that a fair coin is flipped a multiple of three times before coming up heads.
3) [T] Find the probability that a fair coin will come up heads for the second time after an even number of flips.
- Answer
-
Solution: \(\displaystyle 5/9\)
4) [T] Find a series that expresses the probability that a fair coin will come up heads for the second time on a multiple of three flips.
5) [T] The expected number of times that a fair coin will come up heads is defined as the sum over \(\displaystyle n=1,2,…\) of \(\displaystyle n\) times the probability that the coin will come up heads exactly \(\displaystyle n\) times in a row, or \(\displaystyle n/2^{n+1}\). Compute the expected number of consecutive times that a fair coin will come up heads.
- Answer
-
Solution: \(\displaystyle E=\sum_{n=1}^∞n/2^{n+1}=1,\) as can be shown using summation by parts
6) [T] A person deposits \(\displaystyle $10\) at the beginning of each quarter into a bank account that earns \(\displaystyle 4%\) annual interest compounded quarterly (four times a year).
a. Show that the interest accumulated after \(\displaystyle n\) quarters is \(\displaystyle $10(\frac{1.01^{n+1}−1}{0.01}−n).\)
b. Find the first eight terms of the sequence.
c. How much interest has accumulated after \(\displaystyle 2\) years?
7) [T] Suppose that the amount of a drug in a patient’s system diminishes by a multiplicative factor \(\displaystyle r<1\) each hour. Suppose that a new dose is administered every \(\displaystyle N\) hours. Find an expression that gives the amount \(\displaystyle A(n)\) in the patient’s system after \(\displaystyle n\) hours for each \(\displaystyle n\) in terms of the dosage \(\displaystyle d\) and the ratio \(\displaystyle r\). (Hint: Write \(\displaystyle n=mN+k\), where \(\displaystyle 0≤k<N\), and sum over values from the different doses administered.)
- Answer
-
Solution: The part of the first dose after \(\displaystyle n\) hours is \(\displaystyle dr^n\), the part of the second dose is \(\displaystyle dr^{n−N}\), and, in general, the part remaining of the \(\displaystyle mth\) dose is \(\displaystyle dr^{n−mN}\), so \(\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},n=k+mN.\)
8) [T] A certain drug is effective for an average patient only if there is at least \(\displaystyle 1\) mg per kg in the patient’s system, while it is safe only if there is at most \(\displaystyle 2\) mg per kg in an average patient’s system. Suppose that the amount in a patient’s system diminishes by a multiplicative factor of \(\displaystyle 0.9\) each hour after a dose is administered. Find the maximum interval \(\displaystyle N\) of hours between doses, and corresponding dose range \(\displaystyle d\) (in mg/kg) for this \(\displaystyle N\) that will enable use of the drug to be both safe and effective in the long term.
9) Suppose that \(\displaystyle a_n≥0\) is a sequence of numbers. Explain why the sequence of partial sums of \(\displaystyle a_n\) is increasing.
- Answer
-
Solution: \(\displaystyle S_{N+1}=a_{N+1}+S_N≥S_N\)
10) [T] Suppose that \(\displaystyle a_n\) is a sequence of positive numbers and the sequence \(\displaystyle S_n\) of partial sums of \(\displaystyle a_n\) is bounded above. Explain why \(\displaystyle \sum_{n=1}^∞a_n\) converges. Does the conclusion remain true if we remove the hypothesis \(\displaystyle a_n≥0\)?
11) [T] Suppose that \(\displaystyle a_1=S_1=1\) and that, for given numbers \(\displaystyle S>1\) and \(\displaystyle 0<k<1\), one defines \(\displaystyle a_{n+1}=k(S−S_n)\) and \(\displaystyle S_{n+1}=a_{n+1}+S_n\). Does \(\displaystyle S_n\) converge? If so, to what? (Hint: First argue that \(\displaystyle S_n<S\) for all \(\displaystyle n\) and \(\displaystyle S_n\) is increasing.)
- Answer
-
Solution: Since \(\displaystyle S>1, a_2>0,\) and since \(\displaystyle k<1, S_2=1+a_2<1+(S−1)=S\). If \(\displaystyle S_n>S\) for some \(\displaystyle n\), then there is a smallest \(\displaystyle n\). For this \(\displaystyle n, S>S_{n−1}\), so \(\displaystyle S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S\), a contradiction. Thus \(\displaystyle S_n<S\) and \(\displaystyle a_{n+1}>0\) for all \(\displaystyle n\), so \(\displaystyle S_n\) is increasing and bounded by \(\displaystyle S\). Let \(\displaystyle S_∗=\lim S_n\). If \(\displaystyle S_∗<S\), then \(\displaystyle δ=k(S−S_∗)>0\), but we can find n such that \(\displaystyle S_∗−S_n<δ/2\), which implies that \(\displaystyle S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2\), contradicting that Sn is increasing to \(\displaystyle S_∗\). Thus \(\displaystyle S_n→S.\)
12) [T] A version of von Bertalanffy growth can be used to estimate the age of an individual in a homogeneous species from its length if the annual increase in year \(\displaystyle n+1\) satisfies \(\displaystyle a_{n+1}=k(S−S_n)\), with \(\displaystyle S_n\) as the length at year \(\displaystyle n, S\) as a limiting length, and \(\displaystyle k\) as a relative growth constant. If \(\displaystyle S_1=3, S=9,\) and \(\displaystyle k=1/2,\) numerically estimate the smallest value of n such that \(\displaystyle S_n≥8\). Note that \(\displaystyle S_{n+1}=S_n+a_{n+1}.\) Find the corresponding \(\displaystyle n\) when \(\displaystyle k=1/4.\)
13) [T] Suppose that \(\displaystyle \sum_{n=1}^∞a_n\) is a convergent series of positive terms. Explain why \(\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.\)
- Answer
-
Solution: Let \(\displaystyle S_k=\sum_{n=1}^ka_n\) and \(\displaystyle S_k→L\). Then \(\displaystyle S_k\) eventually becomes arbitrarily close to \(\displaystyle L\), which means that \(\displaystyle L−S_N=\sum_{n=N+1}^∞a_n\) becomes arbitrarily small as \(\displaystyle N→∞.\)
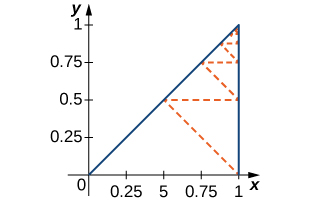
14) [T] Find the length of the dashed zig-zag path in the following figure.
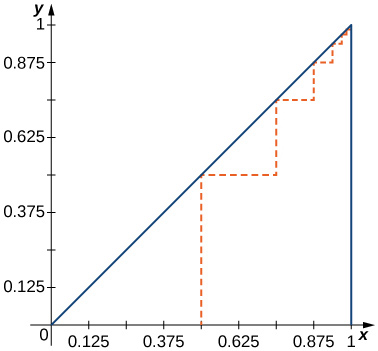
15) [T] Find the total length of the dashed path in the following figure.
- Answer
-
Solution: \(\displaystyle L=(1+\frac{1}{2})\sum_{n=1}^∞1/2^n=\frac{3}{2}\)
16) [T] The Sierpinski triangle is obtained from a triangle by deleting the middle fourth as indicated in the first step, by deleting the middle fourths of the remaining three congruent triangles in the second step, and in general deleting the middle fourths of the remaining triangles in each successive step. Assuming that the original triangle is shown in the figure, find the areas of the remaining parts of the original triangle after \(\displaystyle N\) steps and find the total length of all of the boundary triangles after \(\displaystyle N\) steps.
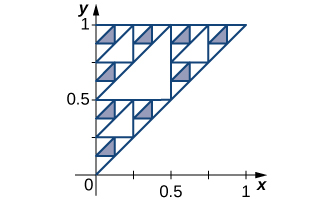
17) [T] The Sierpinski gasket is obtained by dividing the unit square into nine equal sub-squares, removing the middle square, then doing the same at each stage to the remaining sub-squares. The figure shows the remaining set after four iterations. Compute the total area removed after \(\displaystyle N\) stages, and compute the length the total perimeter of the remaining set after \(\displaystyle N\) stages.

- Answer
-
Solution: At stage one a square of area \(\displaystyle 1/9\) is removed, at stage \(\displaystyle 2\) one removes \(\displaystyle 8\) squares of area \(\displaystyle 1/9^2\), at stage three one removes \(\displaystyle 8^2\) squares of area \(\displaystyle 1/9^3\), and so on. The total removed area after \(\displaystyle N\) stages is \(\displaystyle \sum_{n=0}^{N−1}8^N/9^{N+1}=\frac{1}{8}(1−(8/9)^N)/(1−8/9)→1\) as \(\displaystyle N→∞.\) The total perimeter is \(\displaystyle 4+4\sum_{n=0}8^N/3^{N+1}→∞.\)
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


