4.5E: Exercises
- Page ID
- 18592
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
State whether each of the following series converges absolutely, conditionally, or not at all.
1) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}\)
2) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)
- Answer
-
Solution: Does not converge by divergence test. Terms do not tend to zero.
3) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)
4) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)
- Answer
-
Solution: Converges conditionally by alternating series test, since \(\displaystyle \sqrt{n+3}/n\) is decreasing. Does not converge absolutely by comparison with p-series, \(\displaystyle p=1/2\)
5) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}\)
6) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}\)
- Answer
-
Solution: Converges absolutely by limit comparison to \(\displaystyle 3^n/4^n,\) for example.
7) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\frac{n−1}{n})^n\)
8) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\frac{n+1}{n})^n\)
- Answer
-
Solution: Diverges by divergence test since \(\displaystyle \lim_{n→∞}|a_n|=e\).
9) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}sin^2n\)
10) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}cos^2n\)
- Answer
-
Solution: Does not converge. Terms do not tend to zero.
11) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}sin^2(1/n)\)
12) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}cos^2(1/n)\)
- Answer
-
Solution: \(\displaystyle \lim_{n→∞}cos^2(1/n)=1.\) Diverges by divergence test.
13) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}ln(1/n)\)
14) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}ln(1+\frac{1}{n})\)
- Answer
-
Solution: Converges by alternating series test.
15) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)
16) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}\)
- Answer
-
Solution: Converges conditionally by alternating series test. Does not converge absolutely by limit comparison with p-series, \(\displaystyle p=π−e\
17) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}\)
18) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}\)
- Answer
-
Solution: Diverges; terms do not tend to zero
19) \(\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})\) (Hint: \(\displaystyle n^{1/n}≈1+ln(n)/n\) for large \(\displaystyle n\).)
20) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(1−cos(\frac{1}{n}))\) (Hint: \(\displaystyle cos(1/n)≈1−1/n^2\) for large \(\displaystyle n\).)
- Answer
-
Solution: Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series
21) \(\displaystyle \sum^∞_{n=1}(−1)^n+1(\sqrt{n+1}−\sqrt{n})\) (Hint: Rationalize the numerator.)
22) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}})\) (Hint: Cross-multiply then rationalize numerator.)
- Answer
-
Solution: Converges absolutely by limit comparison with p-series, \(\displaystyle p=3/2\), after applying the hint.
23) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(ln(n+1)−lnn)\)
24) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(tan^{−1}(n+1)−tan^{−1}n)\) (Hint: Use Mean Value Theorem.)
- Answer
-
Solution: Converges by alternating series test since \(\displaystyle n(tan^{−1}(n+1)−tan^{−1}n)\) is decreasing to zero for large \(\displaystyle n\).Does not converge absolutely by limit comparison with harmonic series after applying hint.
25) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)\)
26) \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\frac{1}{n}−\frac{1}{n+1})\)
- Answer
-
Solution: Converges absolutely, since \(\displaystyle a_n=\frac{1}{n}−\frac{1}{n+1}\) are terms of a telescoping series.
27) \(\displaystyle \sum^∞_{n=1}\frac{cos(nπ)}{n}\)
28) \(\displaystyle \sum^∞_{n=1}\frac{cos(nπ)}{n^{1/n}}\)
- Answer
-
Solution: Terms do not tend to zero. Series diverges by divergence test.
29) \(\displaystyle \sum^∞_{n=1}\frac{1}{n}sin(\frac{nπ}{2})\)
30) \(\displaystyle \sum^∞_{n=1}sin(nπ/2)sin(1/n)\)
- Answer
-
Solution: Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.
Exercise \(\PageIndex{2}\)
In each of the following problems, use the estimate \(\displaystyle |R_N|≤b_{N+1}\) to find a value of \(\displaystyle N\) that guarantees that the sum of the first N terms of the alternating series \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) differs from the infinite sum by at most the given error. Calculate the partial sum \(\displaystyle S_N\) for this \(\displaystyle N\).
1) [T] \(\displaystyle b_n=1/n,\) error \(\displaystyle <10^{−5}\)
2) [T] \(\displaystyle b_n=1/ln(n), n≥2,\) error \(\displaystyle <10^{−1}\)
- Answer
-
Solution: \(\displaystyle ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…\)
3) [T] \(\displaystyle b_n=1/\sqrt{n},\) error \(\displaystyle <10^{−3}\)
4) [T] \(\displaystyle b_n=1/2^n\), error \(\displaystyle <10^{−6}\)
- Answer
-
Solution: \(\displaystyle 2^{N+1}>10^6\) or \(\displaystyle N+1>6ln(10)/ln(2)=19.93.\) or \(\displaystyle N≥19; S_{19}=0.333333969…\)
5) [T] \(\displaystyle b_n=ln(1+\frac{1}{n}),\) error \(\displaystyle <10^{−3}\)
6) [T] \(\displaystyle b_n=1/n^2,\) error \(\displaystyle <10^{−6}\)
- Answer
-
Solution: \(\displaystyle (N+1)^2>10^6\) or \(\displaystyle N>999; S_{1000}≈0.822466.\)
Exercise \(\PageIndex{3}\)
For the following exercises, indicate whether each of the following statements is true or false. If the statement is false, provide an example in which it is false.
1) If \(\displaystyle b_n≥0\) is decreasing and \(\displaystyle \lim_{n→∞}b_n=0\), then \(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converges absolutely.
2) If \(\displaystyle b_n≥0\) is decreasing, then \(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converges absolutely.
- Answer
-
Solution: True. \(\displaystyle b_n\) need not tend to zero since if \(\displaystyle c_n=b_n−\lim b_n\), then \(\displaystyle c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)
3) If \(\displaystyle b_n≥0\) and \(\displaystyle \lim_{n→∞}b_n=0\) then \(\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) converges.
4) If \(\displaystyle b_n≥0\) is decreasing and \(\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})\) converges then \(\displaystyle \sum_{n=1}^∞b_{3n−2}\) converges.
- Answer
-
Solution: True. \(\displaystyle b_{3n−1}−b_{3n}≥0,\) so convergence of \(\displaystyle \sum b_{3n−2}\) follows from the comparison test.
5) If \(\displaystyle b_n≥0\) is decreasing and \(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converges conditionally but not absolutely, then \(\displaystyle b_n\) does not tend to zero.
6) Let \(\displaystyle a^+_n=a_n\) if \(\displaystyle a_n≥0\) and \(\displaystyle a^−_n=−a_n\) if \(\displaystyle a_n<0\). (Also, \(\displaystyle a+n=0\) if \(\displaystyle a_n<0\) and \(\displaystyle a−n=0\) if \(\displaystyle a_n≥0\).) If \(\displaystyle \sum_{n=1}^∞a_n\) converges conditionally but not absolutely, then neither \(\displaystyle \sum_{n=1}^∞a^+_n\) nor \(\displaystyle \sum_{n=1}^∞a^−_n\) converge.
- Answer
-
Solution: True. If one converges, then so must the other, implying absolute convergence.
7) Suppose that \(\displaystyle a_n\) is a sequence of positive real numbers and that \(\displaystyle \sum_{n=1}^∞a_n\) converges.
8) Suppose that \(\displaystyle b_n\) is an arbitrary sequence of ones and minus ones. Does \(\displaystyle \sum_{n=1}^∞a_nb_n\) necessarily converge?
- Answer
-
Solution: Yes. Take \(\displaystyle b_n=1\) if \(\displaystyle a_n≥0\) and \(\displaystyle b_n=0\) if \(\displaystyle a_n<0\). Then \(\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:an≥0}a_n\) converges. Similarly, one can show \(\displaystyle \sum_{n:an<0}a_n\) converges. Since both series converge, the series must converge absolutely.
9) Suppose that \(\displaystyle a_n\) is a sequence such that \(\displaystyle \sum_{n=1}^∞a_nb_n\) converges for every possible sequence \(\displaystyle b_n\) of zeros and ones. Does \(\displaystyle \sum_{n=1}^∞a_n\) converge absolutely?
Exercise \(\PageIndex{4}\)
The following series do not satisfy the hypotheses of the alternating series test as stated. In each case, state which hypothesis is not satisfied. State whether the series converges absolutely.
1) \(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{sin^2n}{n}\)
2) \(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{cos^2n}{n}\)
- Answer
-
Solution: Not decreasing. Does not converge absolutely.
3) \(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯\)
4) \(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯\)
- Answer
-
Solution: Not alternating. Can be expressed as \(\displaystyle \sum_{n=1}^∞(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}),\) which diverges by comparison with \(\displaystyle \sum\frac{1}{3n−2}.\)
5) Show that the alternating series \(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}[8]+⋯\) does not converge. What hypothesis of the alternating series test is not met?
6) Suppose that \(\displaystyle \sum a_n\) converges absolutely. Show that the series consisting of the positive terms \(\displaystyle a_n\) also converges.
- Answer
-
Solution: Let \(\displaystyle a^+_n=a_n\) if \(\displaystyle a_n≥0\) and \(\displaystyle a^+_n=0\) if \(\displaystyle a_n<0\). Then \(\displaystyle a^+_n≤|a_n|\) for all \(\displaystyle n\) so the sequence of partial sums of \(\displaystyle a^+_n\) is increasing and bounded above by the sequence of partial sums of \(\displaystyle |a_n|\), which converges; hence, \(\displaystyle \sum_{n=1}^∞a^+_n\) converges.
7) Show that the alternating series \(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯\) does not converge. What hypothesis of the alternating series test is not met?
8) The formula \(\displaystyle cosθ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) will be derived in the next chapter. Use the remainder \(\displaystyle |R_N|≤b_{N+1}\) to find a bound for the error in estimating \(\displaystyle cosθ\) by the fifth partial sum \(\displaystyle 1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!\) for \(\displaystyle θ=1, θ=π/6,\) and \(\displaystyle θ=π.\)
- Answer
-
Solution: For \(\displaystyle N=5\) one has \(\displaystyle ∣R_N∣b_6=θ^{10}/10!\). When \(\displaystyle θ=1, R_5≤1/10!≈2.75×10^{−7}\). When \(\displaystyle θ=π/6,\) \(\displaystyle R_5≤(π/6)^{10}/10!≈4.26×10^{−10}\). When \(\displaystyle θ=π, R_5≤π^{10}/10!=0.0258.\)
9) The formula \(\displaystyle sinθ=θ−\frac{θ^3}{3!}+\frac{θ^5}{5!}−\frac{θ^7}{7!}+⋯\) will be derived in the next chapter. Use the remainder \(\displaystyle |R_N|≤b_{N+1}\) to find a bound for the error in estimating \(\displaystyle sinθ\) by the fifth partial sum \(\displaystyle θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!\) for \(\displaystyle θ=1, θ=π/6,\) and \(\displaystyle θ=π.\)
10) How many terms in \(\displaystyle cosθ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) are needed to approximate \(\displaystyle cos1\) accurate to an error of at most \(\displaystyle 0.00001\)?
- Answer
-
Solution: Let \(\displaystyle b_n=1/(2n−2)!.\) Then \(\displaystyle R_N≤1/(2N)!<0.00001\) when \(\displaystyle (2N)!>10^5\) or \(\displaystyle N=5\) and \(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…\), whereas \(\displaystyle cos1=0.5403023…\)
11) How many terms in \(\displaystyle sinθ=θ−\frac{θ^3}{3!}+\frac{θ^5}{5!}−\frac{θ^7}{7!}+⋯\) are needed to approximate \(\displaystyle sin1\) accurate to an error of at most \(\displaystyle 0.00001?\)
12) Sometimes the alternating series \(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converges to a certain fraction of an absolutely convergent series \(\displaystyle \sum_{n=1}^∞b_n\) at a faster rate. Given that \(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}\), find \(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯\). Which of the series \(\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}\) and \(\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}\) gives a better estimation of \(\displaystyle π^2\) using \(\displaystyle 1000\) terms?
- Answer
-
Solution: Let \(\displaystyle T=\sum\frac{1}{n^2}.\) Then \(\displaystyle T−S=\frac{1}{2}T\), so \(\displaystyle S=T/2\). \(\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….\) The alternating series is more accurate for \(\displaystyle 1000\) terms.
Exercise \(\PageIndex{5}\)
The following alternating series converge to given multiples of \(\displaystyle π\). Find the value of \(\displaystyle N\) predicted by the remainder estimate such that the \(\displaystyle Nth\) partial sum of the series accurately approximates the left-hand side to within the given error. Find the minimum \(\displaystyle N\) for which the error bound holds, and give the desired approximate value in each case. Up to \(\displaystyle 15\) decimals places, \(\displaystyle π=3.141592653589793….\)
1) [T] \(\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},\) error \(\displaystyle <0.0001\)
2) [T] \(\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},\) error \(\displaystyle <0.0001\)
- Answer
-
Solution: \(\displaystyle N=6, S_N=0.9068\)
3) [T] The series \(\displaystyle \sum_{n=0}^∞\frac{sin(x+πn)}{x+πn}\) plays an important role in signal processing. Show that \(\displaystyle \sum_{n=0}^∞\frac{sin(x+πn)}{x+πn}\) converges whenever \(\displaystyle 0<x<π\). (Hint: Use the formula for the sine of a sum of angles.)
4) [T] If \(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,\) what is \(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?\)
- Answer
-
Solution: \(\displaystyle ln(2).\) The \(\displaystyle 3nth\) partial sum is the same as that for the alternating harmonic series.
5) [T] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{cos(2πnx)}{n}\) for \(\displaystyle 0≤x<1\). Explain why \(\displaystyle \sum_{n=1}^{100}\frac{cos(2πnx)}{n}\) diverges when \(\displaystyle x=0,1\). How does the series behave for other \(\displaystyle x\)?
6) [T] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{sin(2πnx)}{n}\) for \(\displaystyle 0≤x<1\) and comment on its behavior.
- Answer
-
Solution: The series jumps rapidly near the endpoints. For \(\displaystyle x\) away from the endpoints, the graph looks like \(\displaystyle π(1/2−x)\).
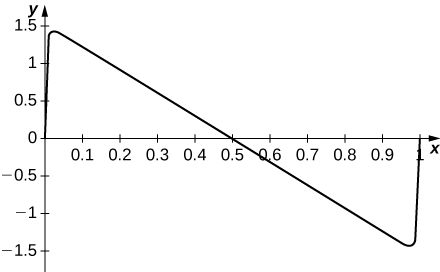
7) [T] Plot the series \(\displaystyle \sum_{n=1}^{100}\frac{cos(2πnx)}{n^2}\) for \(\displaystyle 0≤x<1\) and describe its graph.
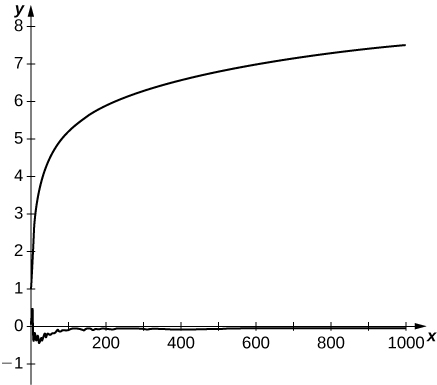
8) [T] The alternating harmonic series converges because of cancellation among its terms. Its sum is known because the cancellation can be described explicitly. A random harmonic series is one of the form \(\displaystyle \sum_{n=1}^∞\frac{S_n}{n}\), where \(\displaystyle s_n\) is a randomly generated sequence of \(\displaystyle ±1's\) in which the values \(\displaystyle ±1\) are equally likely to occur. Use a random number generator to produce \(\displaystyle 1000\) random \(\displaystyle ±1s\) and plot the partial sums \(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) of your random harmonic sequence for \(\displaystyle N=1\) to \(\displaystyle 1000\). Compare to a plot of the first \(\displaystyle 1000\) partial sums of the harmonic series.
- Answer
-
Solution: Here is a typical result. The top curve consists of partial sums of the harmonic series. The bottom curve plots partial sums of a random harmonic series.
9) [T] Estimates of \(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) can be accelerated by writing its partial sums as \(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) and recalling that \(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) converges to one as \(\displaystyle N→∞.\) Compare the estimate of \(\displaystyle π^2/6\) using the sums \(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) with the estimate using \(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).
10) [T] The Euler transform rewrites \(\displaystyle S=\sum_{n=0}^∞(−1)^nb_n\) as \(\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). For the alternating harmonic series, it takes the form \(\displaystyle ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}\). Compute partial sums of \(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) until they approximate \(\displaystyle ln(2)\) accurate to within \(\displaystyle 0.0001\). How many terms are needed? Compare this answer to the number of terms of the alternating harmonic series are needed to estimate \(\displaystyle ln(2)\).
- Answer
-
Solution: By the alternating series test, \(\displaystyle |S_n−S|≤b_{n+1},\) so one needs \(\displaystyle 10^4\) terms of the alternating harmonic series to estimate \(\displaystyle ln(2)\) to within \(\displaystyle 0.0001\). The first \(\displaystyle 10\) partial sums of the series \(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) are (up to four decimals) \(\displaystyle 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) and the tenth partial sum is within \(\displaystyle 0.0001\) of \(\displaystyle ln(2)=0.6931….\)
11) [T] In the text it was stated that a conditionally convergent series can be rearranged to converge to any number. Here is a slightly simpler, but similar, fact. If \(\displaystyle a_n≥0\) is such that \(\displaystyle a_n→0\) as \(\displaystyle n→∞\) but \(\displaystyle \sum_{n=1}^∞a_n\) diverges, then, given any number \(\displaystyle A\) there is a sequence \(\displaystyle s_n\) of \(\displaystyle ±1's\) such that \(\displaystyle \sum_{n=1}^∞a_ns_n→A.\) Show this for \(\displaystyle A>0\) as follows.
a. Recursively define \(\displaystyle s_n\) by \(\displaystyle s_n=1\) if \(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) and \(\displaystyle s_n=−1\) otherwise.
b. Explain why eventually \(\displaystyle S_n≥A,\) and for any \(\displaystyle m\) larger than this \(\displaystyle n\), \(\displaystyle A−a_m≤S_m≤A+a_m\).
c. Explain why this implies that \(\displaystyle S_n→A\) as \(\displaystyle n→∞.\)

