3.2E: Exercises
- Page ID
- 18790
This page is a draft and is under active development.
Exercises
Exercise \(\PageIndex{1}\)
Find the general solution.
(a) \(y'+ay=0\) (\(a\)=constant)
(b) \(y'+3x^2y=0\)
(c) \(xy'+(\ln x)y=0\)
(d) \(xy'+3y=0\)
(e) \(x^2y'+y=0\)
- Answer
-
(a) Since \(y'/y=-a \), \(y=e^{-ax+c}\).
(b)Since \(y'/y=-3x^2 \), \(y=e^{-x^3+c}\).
(c)Since \(y'/y=\frac{-\ln(x)}{x} \), \(y=e^{\frac{-1}{2}\ln^2(x)+c}\).
(d)Since \(y'/y=\frac{-3}{x} \), \(y=\frac{c}{x^3}\).
(e)Since \(y'/y=\frac{-1}{x^2} \), \( y=e^{\frac{-1}{x}+c}\).
Exercise \(\PageIndex{2}\)
Solve the initial value problem.
(a) \({y'+\left({1+x\over x}\right)y=0,\quad y(1)=1}\)
(b) \({xy'+\left(1+{1\over\ln x}\right)y=0,\quad y(e)=1}\)
(c) \({xy'+(1+ x\cot x)y=0,\quad y\left({\pi\over 2} \right)=2}\)
(d) \({y'-\left({2x\over 1+x^2}\right)y=0,\quad y(0)=2}\)
(e) \({y'+{k\over x}y=0,\quad y(1)=3 \quad {(k=constant)}}\)
(f) \( y'+(\tan kx)y=0,\quad y(0)=2 \quad {(k=constant)}\)
- Answer
-
(a) Since \(y=\frac{e^{-x+c}}{x}\) and \( y(1)=1\), then \(c=1\).
(b) Since \(y=\frac{c}{x\ln(x)}\) and \( y(e)=1\), then \(c=1\).
(c) Since \(y=\frac{c}{x\sin(x)}\) and \(y(\frac{\pi}{2})=2\), then \(c=\frac{\pi}{2}\).
(d) Since \(y=(1+x^2)e^c\) and \(y(0)=2\), \(c=\ln(2)\).
(e) Since \(y=\frac{c}{x^k}\) and \(y(1)=3\), \(c=3\). Compare treatment of \(c\) in (d) and (e). In (e) \(c=e^{c_0}=3\) versus in (d) \(e^c=2\).
(f) Since \(y=e^c\cos^{\frac{1}{k}}(kx)\) and \(y(0)=2\), \(c=\ln(2)\).
Exercise \(\PageIndex{3}\)
Find the general solution. Also, plot a direction field and some integral curves on the rectangular region \(\{-2\le x\le2,\ -2\le y\le2\)\}.}
(a) \(y'+3y=1\)
(b) \({y'+\left({1\over x}-1\right)y=-{2\over x}}\)
(c) \(y'+2xy=xe^{-x^2}\)
(d) \({y'+{2x\over1+x^2}y={e^{-x}\over1+x^2}}\)
- Answer
-
(a) \( y=\frac{1}{3}+\frac{c}{e^{3x}}\)
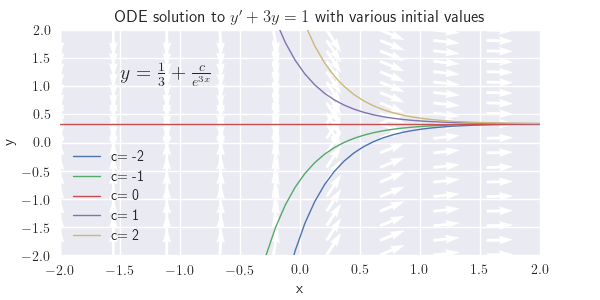
(b) \( y = \frac{2}{x}+\frac{ce^x}{x} \)
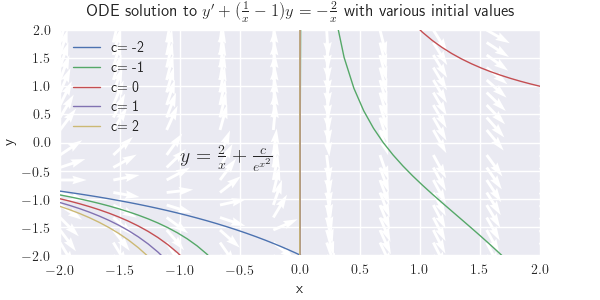
Figure \(\PageIndex{1}\): \(y' + (\frac{1}{x}-1)y =-\frac{2}{x}\) (c) \( y = \frac{x^2}{2e^{x^2}} + \frac{c}{e^{x^2}} \)
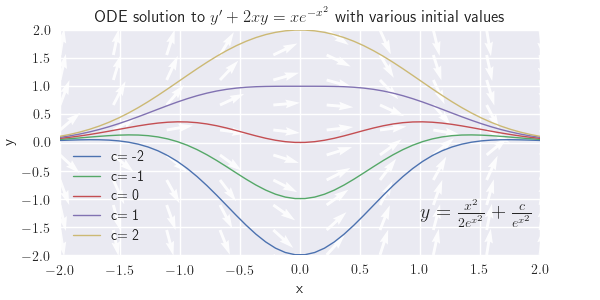
Figure \(\PageIndex{1}\): \(y'+2xy=xe^{-x^2}\) (d) \( y= \frac{-1}{e^x(1+x^2)} + \frac{c}{1+x^2} \)
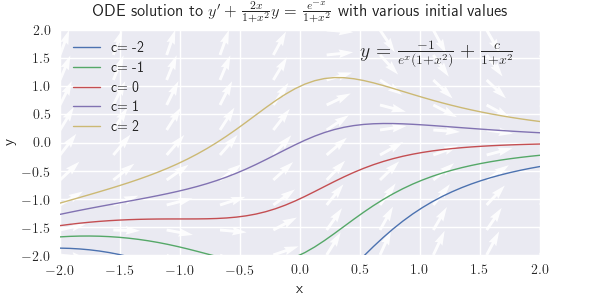
Figure \(\PageIndex{1}\): \(y'+\frac{2x}{1+x^2}y=\frac{e^{-x}}{1+x^2}\)
Exercise \(\PageIndex{4}\)
Find the general solution.
(a) \({y'+{1\over x}y={7\over x^2}+3}\)
(b) \({y'+{4\over x-1}y = {1\over (x-1)^5}+{\sin x\over (x-1)^4}}\)
(c) \(xy'+(1+2x^2)y=x^3e^{-x^2}\)
(d) \({xy'+2y={2\over x^2}+1}\)
(e) \(y'+(\tan x)y=\cos x\)
(f) \({(1+x)y'+2y={\sin x \over 1 + x}}\)
(g) \((x-2)(x-1)y'-(4x-3)y=(x-2)^3\)
(h) \(y'+(2\sin x\cos x) y=e^{-\sin^2x}\)
(i) \(x^2y'+3xy=e^x\)
- Answer
-
(a) \( y = \frac{7\ln(x)}{x}+\frac{3x}{2}+\frac{c}{x}\)
(c) \( y = \frac{x^3}{4e^{x^2}} + \frac{c}{xe^{x^2}} \)
(e) \(y = x\cos(x)+c\cos(x)\)
(g) \(y= \frac{-(x-2)^3}{4(x-1)}+\frac{c(x-2)^5}{x-1}\) Hint: Use partial fractions.
(i) \(y=\frac{(x-1)e^x}{x^3}+\frac{c}{x^3}\)
Exercise \(\PageIndex{5}\)
Solve the initial value problem and sketch the graph of the solution.
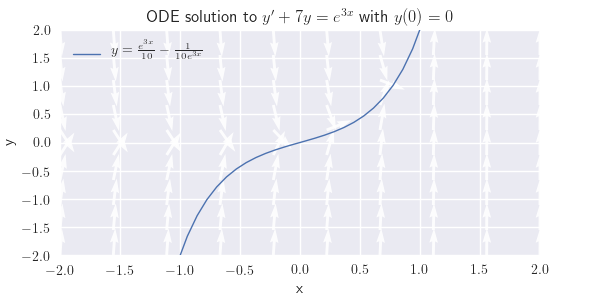
(a) \(y'+7y=e^{3x},\quad y(0)=0\)
(b) \({(1+x^2)y'+4xy={2\over 1+x^2},\quad y(0)=1}\)
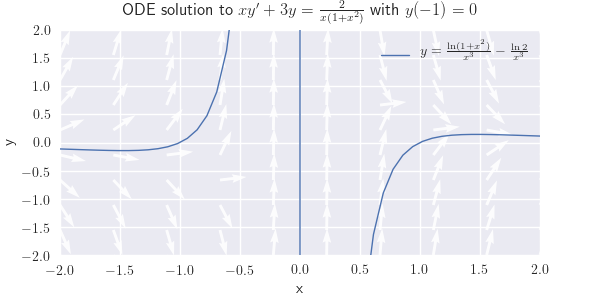
(c) \({xy'+3y={2\over x(1+x^2)},\quad y(-1)=0}\)
(d) \({y'+ (\cot x)y=\cos x,\quad y\left({\pi\over 2}\right)=1}\)
(e) \({y'+{1\over x}y={2\over x^2}+1,\quad y(-1)=0}\)
- Answer
-
(a) \(y=\frac{e^{3x}}{10}-\frac{1}{10e^{3x}} \)
(c) \(y=\frac{\ln(1+x^2)}{x^3}-\frac{\ln{2}}{x^3}\)
(e) \(y=\frac{\ln(x^2)}{x}+1+\frac{1}{x}\)

Exercise \(\PageIndex{6}\)
Solve the initial value problem.
(a) \({(x-1)y'+3y={1\over (x-1)^3} + {\sin x\over (x-1)^2},\quad y(0)=1}\)
(b) \(xy'+2y=8x^2,\quad y(1)=3\)
(c) \(xy'-2y=-x^2,\quad y(1)=1\)
(d) \(y'+2xy=x,\quad y(0)=3\)
(e) \({(x-1)y'+3y={1+(x-1)\sec^2x\over (x-1)^3},\quad y(0)=-1}\)
(f) \({(x+2)y'+4y={1+2x^2\over x(x+2)^3},\quad y(-1)=2}\)
(g) \((x^2-1)y'-2xy=x(x^2-1),\quad y(0)=4\)
(h) \((x^2-5)y'-2xy=-2x(x^2-5),\quad y(2)=7\)
- Answer
-
(a) \(y=\frac{ln|x-1|}{(x-1)^3}-\frac{\cos(x)}{(x-1)^3}+\frac{c}{(x-1)^3}\) thus \(c=0\).
(c) \(y=x^2\ln|\frac{1}{x}| + cx^2\) thus \(c=1\).
(e) \(y= \frac{x-\tan(x)+x\tan(x)+\ln|\cos(x)|+c}{(x-1)^3}\) thus \(c=0\).
(f) \(y= \frac{\ln|x|+x^2+c}{(x+2)^4}\) thus \(c=1\).
(h) \(y= (-\ln(x^2-5)+c)(x^2-5)\) thus \(c= -7\).
Exercise \(\PageIndex{7}\)
Solve the initial value problem and leave the answer in a form involving a definite integral.
You can solve these problems numerically by methods discussed in Chapter~3.
(a) \(y'+2xy=x^2,\quad y(0)=3\)
(b) \({y'+{1\over x}y={\sin x\over x^2},\quad y(1)=2}\)
(c) \({y'+y={e^{-x}\tan x\over x},\quad y(1)=0}\)
(d) \({y'+{2x\over 1+x^2}y={e^x\over (1+x^2)^2}, \quad y(0)=1}\)
(e) \(xy'+(x+1)y=e^{x^2},\quad y(1)=2\)
- Answer
-
(a) \(y=(\frac{xe^{x^2}}{2}-\frac{1}{2}\int_0^{x^2} {e^t \, dt}+c)e^{x^{-2}}\), thus \(c=4\).
Exercise \(\PageIndex{8}\)
Experiments indicate that glucose is absorbed by the body at a rate proportional to the amount of glucose present in the bloodstream. Let \(\lambda\) denote the (positive) constant of proportionality. Now suppose glucose is injected into a patient's bloodstream at a constant rate of \(r\) units per unit of time. Let \(G=G(t)\) be the number of units in the patient's bloodstream at time \(t>0\). Then \(G'=-\lambda G+r,\) where the first term on the right is due to the absorption of the glucose by the patient's body and the second term is due to the injection. Determine \(G\) for \(t>0\), given that \(G(0)=G_0\). Also, find \(\lim_{t\to\infty}G(t)\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{9}\)
(a) Plot a direction field and some integral curves for equation A: \(xy'-2y=-1\) on the rectangular region \(\{-1\le x\le 1, -.5\le y\le 1.5\}\). What do all the integral curves have in common?
(b) Show that the general solution of (A) on \((-\infty,0)\) and \((0,\infty)\) is \(y={1\over2}+cx^2.\)
(c) Show that \(y\) is a solution of (A) on \((-\infty,\infty)\) if and only if
\(y=1 \over 2+c_1x^2, x\ge 0\) and \(1\over 2+c_2x^2, x < 0,\).
where \(c_1\) and \(c_2\) are arbitrary constants.
(d) Conclude from \part{c} that all solutions of (A) on \((-\infty,\infty)\) are solutions of the initial value problem \(xy'-2y=-1,\quad y(0)={1\over2}.\)
(e) Use part b to show that if \(x_0\ne0\) and \(y_0\) is arbitrary, then the initial value problem \(xy'-2y=-1,\quad y(x_0)=y_0\) has infinitely many solutions on \((-\infty,\infty)\). Explain why this doesn't contradict Theorem~\ref{thmtype:3.3.1} \part{b}.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{10}\)
Suppose \(f\) is continuous on an open interval \((a,b)\) and \(\alpha\) is a constant.
(a) Derive a formula for the solution of the initial value problem \(y'+\alpha y=f(x),\quad y(x_0)=y_0, \) where \(x_0\) is in \((a,b)\) and \(y_0\) is an arbitrary real number.
(b) Suppose \((a,b)=(a,\infty)\), \(\alpha > 0\) and \(\displaystyle{\lim_{x\to\infty} f(x)=L}\). Show that if \(y\) is the solution of (a), then
\(\displaystyle{\lim_{x\to \infty} y(x)=L/\alpha}\).
Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{11}\)
Assume that all functions in this exercise are defined on a common interval \((a,b)\)
(a) Prove: If \(y_1\) and \(y_2\) are solutions of \(y'+p(x)y=f_1(x)\) and \(y'+p(x)y=f_2(x)\) respectively, and \(c_1\) and \(c_2\) are constants, then \(y=c_1y_1+c_2y_2\) is a solution of \(y'+p(x)y=c_1f_1(x)+c_2f_2(x).\)
(This is the principle of superposition)
(b) Use (a) to show that if \(y_1\) and \(y_2\) are solutions of the nonhomogeneous equation \(y'+p(x)y=f(x),\) then \(y_1-y_2\) is a solution of the homogeneous equation B: \(y'+p(x)y=0\).
(c) Use (a) to show that if \(y_1\) is a solution of (A) and \(y_2\) is a solution of (B), then \(y_1+y_2\) is a solution of (A).
Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{12}\)
Some nonlinear equations can be transformed into linear equations by changing the dependent variable. Show that if \(g'(y)y'+p(x)g(y)=f(x)\) where \(y\) is a function of \(x\) and \(g\) is a function of \(y\), then the new dependent variable \(z=g(y)\) satisfies the linear equation \(z'+p(x)z=f(x).\)
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{13}\)
We've shown that if \(p\) and \(f\) are continuous on \((a,b)\) then every solution of equation A: \(y'+p(x)y=f(x)\) on \((a,b)\) can be written as \(y=uy_1\), where \(y_1\) is a nontrivial solution of the complementary equation for (A) and \(u'=f/y_1\). Now suppose \(f\), \(f'\), \dots, \(f^{(m)}\) and \(p\), \(p'\), \dots, \(p^{(m-1)}\) are continuous on \((a,b)\), where \(m\) is a positive integer, and define \begin{eqnarray*} f_0&=&f,\\ f_j&=&f_{j-1}'+pf_{j-1},\quad 1\le j\le m. \end{eqnarray*}
Show that \(u^{(j+1)}={f_j\over y_1},\quad 0\le j\le m.\)
- Answer
-
Add texts here. Do not delete this text first.

