3.9: Applications
- Page ID
- 25887
This section begins with a discussion of exponential growth and decay, which you have probably already seen in calculus. We consider applications to radioactive decay, carbon dating, and compound interest. We also consider more complicated problems where the rate of change of a quantity is in part proportional to the magnitude of the quantity, but is also influenced by other other factors for example, a radioactive substance is manufactured at a certain rate, but decays at a rate proportional to its mass, or a saver makes regular deposits in a savings account that draws compound interest.
Since the applications in this section deal with functions of time, we’ll denote the independent variable by \(t\). If \(Q\) is a function of \(t\), \(Q'\) will denote the derivative of \(Q\) with respect to \(t\); thus,
\[Q'={dQ\over dt}.\nonumber \]
Exponential Growth and Decay
One of the most common mathematical models for a physical process is the exponential model, where it is assumed that the rate of change of a quantity \(Q\) is proportional to \(Q\); thus
\[\label{eq:3.10.1} Q'=aQ,\]
where \(a\) is the constant of proportionality.
From Example 2.1.3, the general solution of Equation \ref{eq:3.10.1} is
\[Q=ce^{at}\nonumber \]
and the solution of the initial value problem
\[Q'=aQ, \quad Q(t_0)=Q_0\nonumber \]
is
\[\label{eq:3.10.2} Q=Q_0e^{a(t-t_0)}.\]
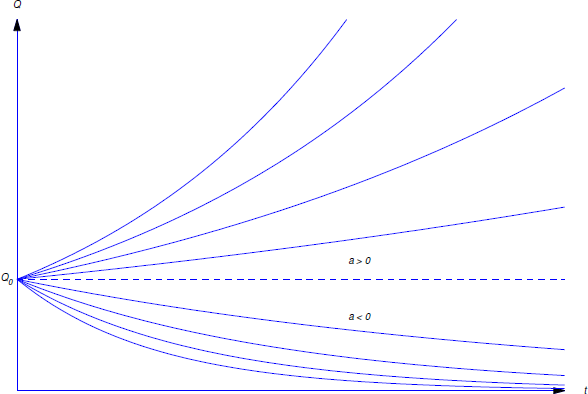
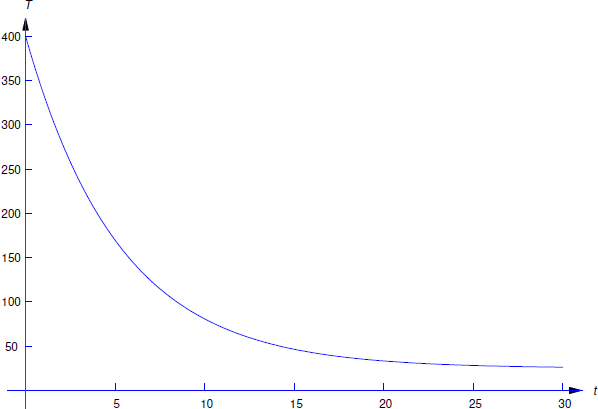
Since the solutions of \(Q'=aQ\) are exponential functions, we say that a quantity \(Q\) that satisfies this equation grows exponentially if \(a > 0\), or decays exponentially if \(a < 0\) (Figure \(\PageIndex{1}\)).
Radioactive Decay
Experimental evidence shows that radioactive material decays at a rate proportional to the mass of the material present. According to this model the mass \(Q(t)\) of a radioactive material present at time \(t\) satisfies Equation \ref{eq:3.10.1}, where \(a\) is a negative constant whose value for any given material must be determined by experimental observation. For simplicity, we’ll replace the negative constant \(a\) by \(-k\), where \(k\) is a positive number that we’ll call the decay constant of the material. Thus, Equation \ref{eq:3.10.1} becomes
\[Q'=-kQ.\nonumber \]
If the mass of the material present at \(t=t_0\) is \(Q_0\), the mass present at time \(t\) is the solution of
\[Q'=-kQ,\quad Q(t_0)=Q_0.\nonumber \]
From Equation \ref{eq:3.10.2} with \(a=-k\), the solution of this initial value problem is
\[\label{eq:3.10.3} Q=Q_0e^{-k(t-t_0)}.\]
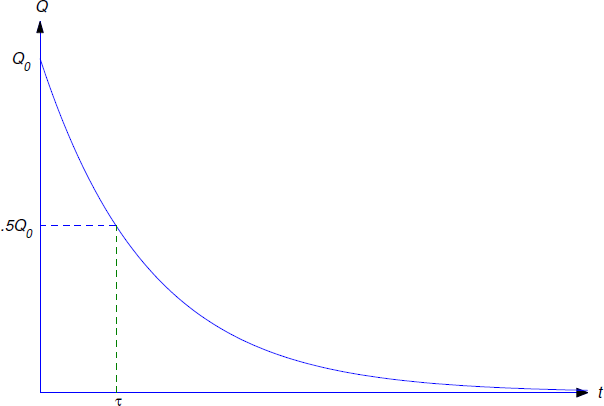
The half–life \(\tau\) of a radioactive material is defined to be the time required for half of its mass to decay; that is, if \(Q(t_0)=Q_0\), then
\[\label{eq:3.10.4} Q(\tau+t_0)={Q_0\over 2}.\]
From Equation \ref{eq:3.10.3} with \(t=\tau+t_0\), Equation \ref{eq:3.10.4} is equivalent to
\[Q_0e^{-k\tau}={Q_0\over 2},\nonumber \]
so
\[e^{-k\tau}={1\over 2}.\nonumber \]
Taking logarithms yields
\[-k\tau=\ln{1\over 2}=-\ln2,\nonumber \]
so the half-life is
\[\label{eq:3.10.5} \tau={1\over k}\ln2.\]
(Figure \(\PageIndex{2}\)). The half-life is independent of \(t_0\) and \(Q_0\), since it is determined by the properties of material, not by the amount of the material present at any particular time.
Example \(\PageIndex{1}\)
A radioactive substance has a half-life of 1620 years.
- If its mass is now 4 g (grams), how much will be left 810 years from now?
- Find the time \(t_1\) when 1.5 g of the substance remain.
Solution a
From Equation \ref{eq:3.10.3} with \(t_0=0\) and \(Q_0=4\),
\[\label{eq:3.10.6} Q=4e^{-kt},\]
where we determine \(k\) from Equation \ref{eq:3.10.5}, with \(\tau\)= 1620 years:\[k={\ln2\over\tau}={\ln2\over 1620}. \nonumber\]
Substituting this in Equation \ref{eq:3.10.6} yields\[\label{eq:3.10.7} Q=4e^{-(t\ln2)/1620}.\]
\[\begin{array}{rl} Q(810) &=4e^{-(810\ln2)/1620}=4e^{-(\ln2)/2} \\ &=2\sqrt{2} \mbox{ g}. \end{array}\nonumber \]
Solution b
Setting \(t=t_1\) in Equation \ref{eq:3.10.7} and requiring that \(Q(t_1)=1.5\) yields
\[{3\over2}=4e^{(-t_1\ln2)/1620}. \nonumber\]
Dividing by 4 and taking logarithms yields\[\ln{3\over8}=-{t_1\ln2\over1620}. \nonumber\]
Since \(\ln3/8=-\ln8/3\),\[t_1=1620{\ln8/3\over\ln2}\approx 2292.4\;\mbox{ years}. \nonumber\]
Interest Compounded Continuously
Suppose we deposit an amount of money \(Q_0\) in an interest-bearing account and make no further deposits or withdrawals for \(t\) years, during which the account bears interest at a constant annual rate \(r\). To calculate the value of the account at the end of \(t\) years, we need one more piece of information: how the interest is added to the account, or—as the bankers say—how it is compounded. If the interest is compounded annually, the value of the account is multiplied by \(1+r\) at the end of each year. This means that after \(t\) years the value of the account is
\[Q(t)=Q_0(1+r)^t. \nonumber \]
If interest is compounded semiannually, the value of the account is multiplied by \((1+r/2)\) every 6 months. Since this occurs twice annually, the value of the account after \(t\) years is\[Q(t)=Q_0\left(1+{r\over 2}\right)^{2t}. \nonumber \]
In general, if interest is compounded \(n\) times per year, the value of the account is multiplied \(n\) times per year by \((1+r/n)\); therefore, the value of the account after \(t\) years is\[\label{eq:3.10.8} Q(t)=Q_0\left(1+{r\over n}\right)^{nt}. \]
Thus, increasing the frequency of compounding increases the value of the account after a fixed period of time. Table \(\PageIndex{1}\) shows the effect of increasing the number of compoundings over \(t=5\) years on an initial deposit of \(Q_0=100\) (dollars), at an annual interest rate of 6%.| \(n\) (number of compoundings per year) | \($100\left(1+\frac{.06}{n} \right)^{5n}\) (value in dollars after 5 years) |
|---|---|
| \(\begin{aligned} &1 \\ &2 \\ &4 \\ &8 \\ &364 \end{aligned}\) | \(\begin{aligned} &$133.82 \\ &$134.39 \\ &$134.68 \\ &$134.83 \\ &$134.98 \end{aligned}\) |
Table \(\PageIndex{1}\): The effect of compound interest
You can see from Table \(\PageIndex{1}\) that the value of the account after 5 years is an increasing function of \(n\). Now suppose the maximum allowable rate of interest on savings accounts is restricted by law, but the time intervals between successive compoundings isn’t; then competing banks can attract savers by compounding often. The ultimate step in this direction is to compound continuously, by which we mean that \(n\to\infty\) in Equation \ref{eq:3.10.8}. Since we know from calculus that
\[\lim_{n\to\infty} \left(1+{r\over n}\right)^n=e^r, \nonumber\]
this yields
\[\begin{array}{rl} Q(t) & =\lim_{n\to\infty} Q_0\left(1+{r\over n}\right)^{nt}=Q_0 \left[ \lim_{n\to\infty} \left(1+{r\over n}\right)^n\right]^t \\[12pt] &=Q_0e^{rt}. \end{array} \nonumber \]
Observe that \(Q=Q_0e^{rt}\) is the solution of the initial value problem
\[Q'=rQ, \quad Q(0)=Q_0; \nonumber\]
that is, with continuous compounding the value of the account grows exponentially.
Example \(\PageIndex{2}\)
If $150 is deposited in a bank that pays \(5{1\over2}\)% annual interest compounded continuously, the value of the account after \(t\) years is
\[Q(t)=150e^{.055t} \nonumber\]
dollars. (Note that it is necessary to write the interest rate as a decimal; thus, \(r=.055\).) Therefore, after \(t=10\) years the value of the account is\[Q(10)=150e^{.55} \approx \$259.99. \nonumber\]
Example \(\PageIndex{3}\)
We wish to accumulate $10,000 in 10 years by making a single deposit in a savings account bearing \(5{1\over2}\)% annual interest compounded continuously. How much must we deposit in the account?
Solution
The value of the account at time \(t\) is
\[\label{eq:3.10.9} Q(t)=Q_0e^{.055t}.\]
Since we want \(Q(10)\) to be $10,000, the initial deposit \(Q_0\) must satisfy the equation\[\label{eq:3.10.10} 10000=Q_0e^{.55},\]
obtained by setting \(t=10\) and \(Q(10)=10000\) in Equation \ref{eq:3.10.9}. Solving Equation \ref{eq:3.10.10} for \(Q_0\) yields\[Q_0=10000e^{-.55} \approx \$5769.50.\nonumber \]
Mixed Growth and Decay
Example \(\PageIndex{4}\)
A radioactive substance with decay constant \(k\) is produced at a constant rate of \(a\) units of mass per unit time.
- Assuming that \(Q(0)=Q_0\), find the mass \(Q(t)\) of the substance present at time \(t\).
- Find \(\lim_{t\to\infty} Q(t)\).
Solution a:
Here
\[Q'=\mbox{ rate of increase of } Q - \mbox{ rate of decrease of } Q.\nonumber \]
The rate of increase is the constant \(a\). Since \(Q\) is radioactive with decay constant \(k\), the rate of decrease is \(kQ\). Therefore\[Q'=a-kQ.\nonumber \]
This is a linear first order differential equation. Rewriting it and imposing the initial condition shows that \(Q\) is the solution of the initial value problem\[\label{eq:3.10.11} Q'+kQ=a, \quad Q(0)=Q_0.\]
Since \(e^{-kt}\) is a solution of the complementary equation, the solutions of Equation \ref{eq:3.10.11} are of the form \(Q=ue^{-kt}\), where \(u'e^{-kt}=a\), so \(u'=ae^{kt}\). Hence,
\[u={a\over k}e^{kt}+c\nonumber \]
\[Q=ue^{-kt}={a\over k}+ce^{-kt}. \nonumber \]
Since \(Q(0)=Q_0\), setting \(t=0\) here yields\[Q_0={a\over k}+c \quad \text{or} \quad c=Q_0-{a\over k}. \nonumber \]
Therefore\[\label{eq:3.10.12} Q={a\over k}+\left(Q_0-{a\over k}\right)e^{-kt}.\]
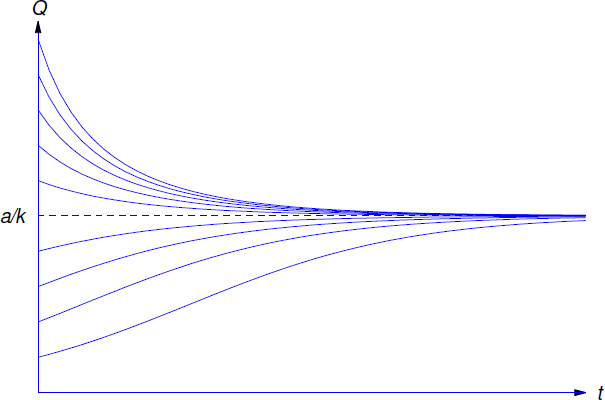
b. Since \(k > 0\), \(\lim_{t\to\infty} e^{-kt}=0\), so from Equation \ref{eq:3.10.12}
\[\lim_{t\to\infty} Q(t)={a\over k}. \nonumber \]
This limit depends only on \(a\) and \(k\), and not on \(Q_0\). We say that \(a/k\) is the steady state value of \(Q\). From Equation \ref{eq:3.10.12} we also see that \(Q\) approaches its steady state value from above if \(Q_0 > a/k\), or from below if \(Q_0 < a/k\). If \(Q_0=a/k\), then \(Q\) remains constant (Figure \(\PageIndex{3}\):).
Carbon Dating
The fact that \(Q\) approaches a steady state value in the situation discussed in Example 4 underlies the method of carbon dating, devised by the American chemist and Nobel Prize Winner W.S. Libby.
Carbon 12 is stable, but carbon-14, which is produced by cosmic bombardment of nitrogen in the upper atmosphere, is radioactive with a half-life of about 5570 years. Libby assumed that the quantity of carbon-12 in the atmosphere has been constant throughout time, and that the quantity of radioactive carbon-14 achieved its steady state value long ago as a result of its creation and decomposition over millions of years. These assumptions led Libby to conclude that the ratio of carbon-14 to carbon-12 has been nearly constant for a long time. This constant, which we denote by \(R\), has been determined experimentally.
Living cells absorb both carbon-12 and carbon-14 in the proportion in which they are present in the environment. Therefore the ratio of carbon-14 to carbon-12 in a living cell is always \(R\). However, when the cell dies it ceases to absorb carbon, and the ratio of carbon-14 to carbon-12 decreases exponentially as the radioactive carbon-14 decays. This is the basis for the method of carbon dating, as illustrated in the next example.
Example \(\PageIndex{5}\)
An archaeologist investigating the site of an ancient village finds a burial ground where the amount of carbon-14 present in individual remains is between 42 and 44% of the amount present in live individuals. Estimate the age of the village and the length of time for which it survived.
Solution
Let \(Q=Q(t)\) be the quantity of carbon-14 in an individual set of remains \(t\) years after death, and let \(Q_0\) be the quantity that would be present in live individuals. Since carbon-14 decays exponentially with half-life 5570 years, its decay constant is
\[k={\ln2\over 5570}. \nonumber\]
Therefore\[Q=Q_0e^{-t(\ln2)/5570}\nonumber\]
if we choose our time scale so that \(t_0=0\) is the time of death. If we know the present value of \(Q\) we can solve this equation for \(t\), the number of years since death occurred. This yields\[t=-5570 {\ln Q/Q_0\over\ln2}.\nonumber\]
It is given that \(Q=.42Q_0\) in the remains of individuals who died first. Therefore these deaths occurred about\[t_1=-5570 {\ln.42\over\ln2} \approx 6971 \nonumber\]
years ago. For the most recent deaths, \(Q=.44 Q_0\); hence, these deaths occurred about\[t_2=-5570 {\ln.44\over\ln2} \approx 6597 \nonumber\]
years ago. Therefore it is reasonable to conclude that the village was founded about 7000 years ago, and lasted for about 400 years.
A Savings Program
Example \(\PageIndex{6}\):
A person opens a savings account with an initial deposit of $1000 and subsequently deposits $50 per week. Find the value \(Q(t)\) of the account at time \(t > 0\), assuming that the bank pays 6% interest compounded continuously.
Solution
Observe that \(Q\) isn’t continuous, since there are 52 discrete deposits per year of $50 each. To construct a mathematical model for this problem in the form of a differential equation, we make the simplifying assumption that the deposits are made continuously at a rate of $2600 per year. This is essential, since solutions of differential equations are continuous functions. With this assumption, \(Q\) increases continuously at the rate
\[Q'=2600+0.06 Q \nonumber\]
and therefore \(Q\) satisfies the differential equation\[\label{eq:3.10.13} Q'-.06Q=2600.\]
(Of course, we must recognize that the solution of this equation is an approximation to the true value of \(Q\) at any given time. We’ll discuss this further below.) Since \(e^{.06t}\) is a solution of the complementary equation, the solutions of Equation \ref{eq:3.10.13} are of the form \(Q=ue^{.06t}\), where \(u'e^{.06t}=2600\). Hence, \(u'=2600e^{-.06t}\),
\[u=- {2600\over.06}e^{-0.06t}+c \nonumber\]
and\[\label{eq:3.10.14} Q=ue^{.06t}=-{2600\over.06}+ce^{.06t}.\]
Setting \(t=0\) and \(Q=1000\) here yields\[c=1000+{2600\over 0.06}, \nonumber\]
and substituting this into Equation \ref{eq:3.10.14} yields\[\label{eq:3.10.15} Q=1000e^{.06t}+{2600\over.06}(e^{.06t}-1) \]
where the first term is the value due to the initial deposit and the second is due to the subsequent weekly deposits.
Mathematical models must be tested for validity by comparing predictions based on them with the actual outcome of experiments. Example 6 is unusual in that we can compute the exact value of the account at any specified time and compare it with the approximate value predicted by Equation \ref{eq:3.10.15} (See Exercise 3.10.21). The following table gives a comparison for a ten year period. Each exact answer corresponds to the time of the year-end deposit, and each year is assumed to have exactly 52 weeks.
| Year | Approximate Value of \(Q\) (Example \(\PageIndex{6}\)) | Exact Value of \(P\) (Exercise 3.10.21) | Error \(Q-P\) | Percentage Error \((Q-P)/P\) |
|---|---|---|---|---|
| \(1\) | \($3741.42\) | \($3739.87\) | \($1.55\) | \(.0413%\) |
| \(2\) | \(6652.36\) | \(6649.17\) | \(3.19\) | \(.0479\) |
| \(3\) | \(9743.30\) | \(9738.37\) | \(4.93\) | \(.0506\) |
| \(4\) | \(13,025.38\) | \(13,018.60\) | \(6.78\) | \(.0521\) |
| \(5\) | \(16,510.41\) | \(16,501.66\) | \(8.75\) | \(.0530\) |
| \(6\) | \(20,210.94\) | \(20,200.11\) | \(10.83\) | \(.0536\) |
| \(7\) | \(24,140.30\) | \(24,127.25\) | \(13.05\) | \(.0541\) |
| \(8\) | \(28,312.63\) | \(28,297.23\) | \(15.40\) | \(.0544\) |
| \(9\) | \(32,742.97\) | \(32,725.07\) | \(17.90\) | \(.0547\) |
| \(10\) | \(37,447.27\) | \(37,426.72\) | \(20.55\) | \(.0549\) |
Table \(\PageIndex{3}\)
Newton’s Law of Cooling
Newton’s law of cooling states that if an object with temperature \(T(t)\) at time \(t\) is in a medium with temperature \(T_m(t)\), the rate of change of \(T\) at time \(t\) is proportional to \(T(t)-T_m(t)\); thus, \(T\) satisfies a differential equation of the form
\[\label{eq:3.10.16} T'=-k(T-T_m).\]
Here \(k > 0\), since the temperature of the object must decrease if \(T > T_m\), or increase if \(T < T_m\). We’ll call \(k\) the temperature decay constant of the medium.
For simplicity, in this section we’ll assume that the medium is maintained at a constant temperature \(T_m\). This is another example of building a simple mathematical model for a physical phenomenon. Like most mathematical models it has its limitations. For example, it is reasonable to assume that the temperature of a room remains approximately constant if the cooling object is a cup of coffee, but perhaps not if it is a huge cauldron of molten metal. (For more on this see Exercise 3.10.17.)
To solve Equation \ref{eq:3.10.16}, we rewrite it as
\[T'+kT=kT_m. \nonumber\]
Since \(e^{-kt}\) is a solution of the complementary equation, the solutions of this equation are of the form \(T=ue^{-kt}\), where \(u'e^{-kt}=kT_m\), so \(u'=kT_me^{kt}\). Hence,
\[u=T_me^{kt}+c, \nonumber\]
so
\[T=ue^{-kt}=T_m+ce^{-kt}. \nonumber\]
If \(T(0)=T_0\), setting \(t=0\) here yields \(c=T_0-T_m\), so
\[\label{eq:3.10.17} T=T_m+(T_0-T_m)e^{-kt}. \]
Note that \(T-T_m\) decays exponentially, with decay constant \(k\).
Example \(\PageIndex{7}\)
A ceramic insulator is baked at \(400^\circ\)C and cooled in a room in which the temperature is \(25^\circ\)C. After 4 minutes the temperature of the insulator is \(200^\circ\)C. What is its temperature after 8 minutes?
Solution
Here \(T_0=400\) and \(T_m=25\), so Equation \ref{eq:3.10.17} becomes
\[\label{eq:3.10.18} T=25+375e^{-kt}.\]
We determine \(k\) from the stated condition that \(T(4)=200\); that is,
\[200=25+375e^{-4k}; \nonumber\]
hence,
\[e^{-4k} = {175\over 375} = {7\over 15}. \nonumber\]
Taking logarithms and solving for \(k\) yields
\[k=-{1\over 4} \ln {7\over 15}={1\over 4}\ln {15\over 7}. \nonumber\]
Substituting this into Equation \ref{eq:3.10.18} yields
\[T=25+375 e^{-{t\over 4} \ln {15\over 7}} \nonumber\]
(Figure \(\PageIndex{4}\)). Therefore the temperature of the insulator after 8 minutes is
\[\begin{array}{rl} T(8) & = 25+375 e^{-2 \ln {15\over 7}} \\[9pt] & = 25+375 \left({7\over 15}\right)^2 \approx 107^\circ \mbox{C}. \end{array}\nonumber \]
Example \(\PageIndex{8}\)
An object with temperature \(72^\circ\)F is placed outside, where the temperature is \(-20^\circ\)F. At 11:05 the temperature of the object is \(60^\circ\)F and at 11:07 its temperature is \(50^\circ\)F. At what time was the object placed outside?
Solution
Let \(T(t)\) be the temperature of the object at time \(t\). For convenience, we choose the origin \(t_0=0\) of the time scale to be 11:05 so that \(T_0=60\). We must determine the time \(\tau\) when \(T(\tau)=72\). Substituting \(T_0=60\) and \(T_m=-20\) into Equation \ref{eq:3.10.17} yields
\[T = -20+\bigl(60-(-20)\bigr)e^{-kt}\nonumber\]
or
\[\label{eq:3.10.19} T = -20+80e^{-kt}. \]
We obtain \(k\) from the stated condition that the temperature of the object is 50\(^\circ\)F at 11:07. Since 11:07 is \(t=2\) on our time scale, we can determine \(k\) by substituting \(T=50\) and \(t=2\) into Equation \ref{eq:3.10.19} to obtain
\[50 = -20+80e^{-2k}\nonumber\]
This is shown in Figure \(\PageIndex{5}\).
Hence,
\[e^{-2k}={70\over 80}={7\over 8}.\nonumber\]
Taking logarithms and solving for \(k\) yields
\[k =-{1\over 2} \ln {7\over 8} = {1\over 2} \ln {8\over 7}.\nonumber\]
Substituting this into Equation \ref{eq:3.10.4} yields
\[T = -20+80 e^{-{t\over 2}\ln {8\over 7}},\nonumber\]
and the condition \(T(\tau)=72\) implies that
\[72 =-20+80 e^{-{\tau\over 2} \ln {8\over 7}};\nonumber\]
hence,
\[e^{-{\tau\over 2} \ln {8\over 7}} ={92\over 80} = {23\over 20}.\nonumber\]
Taking logarithms and solving for \(\tau\) yields
\[\tau = -{2 \ln {23\over 20}\over \ln {8\over 7}} \approx-2.09\ \mbox{min}.\nonumber\]
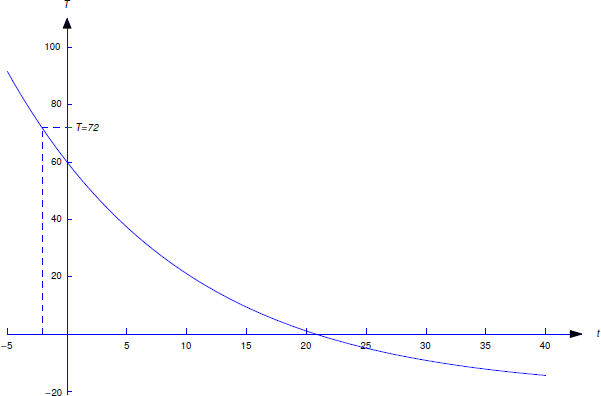
Therefore the object was placed outside about 2 minutes and 5 seconds before 11:05; that is, at 11:02:55.
Mixing Problems
In the next two examples a saltwater solution with a given concentration (weight of salt per unit volume of solution) is added at a specified rate to a tank that initially contains saltwater with a different concentration. The problem is to determine the quantity of salt in the tank as a function of time. This is an example of a mixing problem. To construct a tractable mathematical model for mixing problems we assume in our examples (and most exercises) that the mixture is stirred instantly so that the salt is always uniformly distributed throughout the mixture. Exercises 3.10.22 and 3.10.23 deal with situations where this isn’t so, but the distribution of salt becomes approximately uniform as \(t\to\infty\).
Example \(\PageIndex{9}\)
A tank initially contains 40 pounds of salt dissolved in 600 gallons of water. Starting at \(t_0 = 0\), water that contains 1/2 pound of salt per gallon is poured into the tank at the rate of 4 gal/min and the mixture is drained from the tank at the same rate (Figure \(\PageIndex{3}\)).
- Find a differential equation for the quantity \(Q(t)\) of salt in the tank at time \(t > 0\), and solve the equation to determine \(Q(t)\).
- Find \(\lim_{t\to\infty}Q(t)\).
Solution a
To find a differential equation for \(Q\), we must use the given information to derive an expression for \(Q'\). But \(Q'\) is the rate of change of the quantity of salt in the tank changes with respect to time; thus, if rate in denotes the rate at which salt enters the tank and rate out denotes the rate by which it leaves, then
\[\label{eq:3.10.20} Q' = \mbox{rate in}-\mbox{rate out}.\]
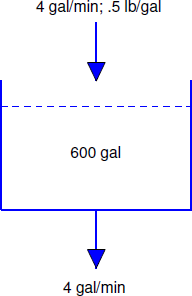
The rate in is
\[\left({1\over 2}\ \mbox{lb/gal}\right) \times (4\ \mbox{gal/min}) = 2\ \mbox{lb/min}.\nonumber\]
Determining the rate out requires a little more thought. We’re removing 4 gallons of the mixture per minute, and there are always 600 gallons in the tank; that is, we are removing \(1/150\) of the mixture per minute. Since the salt is evenly distributed in the mixture, we are also removing \(1/150\) of the salt per minute. Therefore, if there are \(Q(t)\) pounds of salt in the tank at time \(t\), the rate out at any time \(t\) is \(Q(t)/150\). Alternatively, we can arrive at this conclusion by arguing that
\[\begin{array}{lcl} \mbox{rate out} & = & (\mbox{concentration})\times(\mbox{rate of flow out})\\[6pt] \mbox{}&=&(\mbox{lb/gal})\times(\mbox{gal/min})\\[10pt] &=&{Q(t)\over600}\times 4={Q(t)\over150}. \end{array}\nonumber \]
We can now write Equation \ref{eq:3.10.20} as
\[Q' = 2-{Q\over 150}. \nonumber\]
This first order equation can be rewritten as
\[Q'+{Q\over 150} = 2. \nonumber\]
Since \(e^{-t/150}\) is a solution of the complementary equation, the solutions of this equation are of the form \(Q=ue^{-t/150}\), where \(u'e^{-t/150}=2\), so \(u'=2e^{t/150}\). Hence,
\[u = 300e^{t/150}+c, \nonumber\]
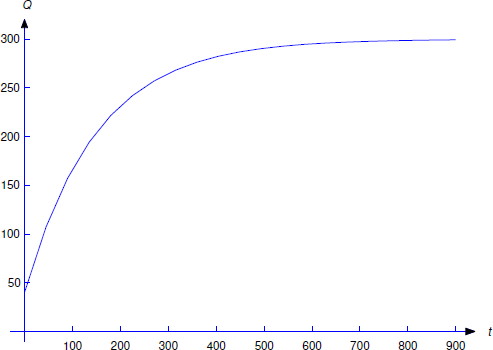
so
\[\label{eq:3.10.21} Q=ue^{-t/150}=300+ce^{-t/150}\]
(Figure \(\PageIndex{7}\)). Since \(Q(0)=40\), \(c=-260\); therefore,
\[Q=300-260e^{-t/150}.\nonumber\]
Solution b
From Equation \ref{eq:3.10.21}, we see that that \(\lim_{t \to \infty}Q(t)=300\) for any value of \(Q(0)\). This is intuitively reasonable, since the incoming solution contains 1/2 pound of salt per gallon and there are always 600 gallons of water in the tank.
Example \(\PageIndex{10}\)
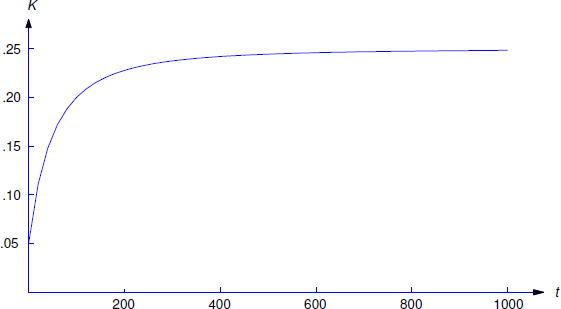
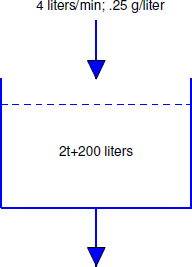
A 500-liter tank initially contains 10 g of salt dissolved in 200 liters of water. Starting at \(t_0=0\), water that contains 1/4 g of salt per liter is poured into the tank at the rate of 4 liters/min and the mixture is drained from the tank at the rate of 2 liters/min (Figure [figure:3.10.8}). Find a differential equation for the quantity \(Q(t)\) of salt in the tank at time \(t\) prior to the time when the tank overflows and find the concentration \(K(t)\) (g/liter) of salt in the tank at any such time.
Solution
We first determine the amount \(W(t)\) of solution in the tank at any time \(t\) prior to overflow. Since \(W(0) = 200\) and we are adding 4 liters/min while removing only 2 liters/min, there’s a net gain of 2 liters/min in the tank; therefore,
\[W(t) = 2t+200.\nonumber\]
Since \(W(150)=500\) liters (capacity of the tank), this formula is valid for \(0 \le t \le 150\).
Now let \(Q(t)\) be the number of grams of salt in the tank at time \(t\), where \(0 \le t \le 150\). As in Example \(\PageIndex{9}\)
\[\label{eq:3.10.22} Q' = \mbox{rate in}-\mbox{rate out}.\]
\[\label{eq:3.10.23} \left({1\over 4}\ \mbox{g/liter}\,\right) \times (4\ \mbox{liters/min}\,) = 1\ \mbox{g/min}.\]
To determine the rate out, we observe that since the mixture is being removed from the tank at the constant rate of 2 liters/min and there are \(2t+200\) liters in the tank at time \(t\), the fraction of the mixture being removed per minute at time \(t\) is\[{2\over 2t+200} = {1\over t+100}.\nonumber\]
We’re removing this same fraction of the salt per minute. Therefore, since there are \(Q(t)\) grams of salt in the tank at time \(t\),\[\label{eq:3.10.24} \mbox{rate out} = {Q(t)\over t+100}.\]
Alternatively, we can arrive at this conclusion by arguing that\[\begin{array}{lcl} \mbox{rate out} & = & (\mbox{concentration})\times(\mbox{rate of flow out}) =(\mbox{g/liter})\times(\mbox{liters/min})\\[10pt] &=&{Q(t)\over2t+200}\times 2={Q(t)\over t+100}. \end{array} \nonumber \]
Substituting Equation \ref{eq:3.10.23} and Equation \ref{eq:3.10.24} into Equation \ref{eq:3.10.22} yields\[\label{eq:3.10.25} Q'=1-{Q\over t+100},\quad \text{so} \quad Q'+{1\over t+100} Q=1.\]
By separation of variables, \(1/(t+100)\) is a solution of the complementary equation, so the solutions of Equation \ref{eq:3.10.25} are of the form\[Q={u\over t+100}, \quad \text{where} \quad {u'\over t+100 =1}, \quad \text{so} \quad u'=t+100.\nonumber\]
Hence,\[\label{eq:3.10.26} u = {(t+100)^2\over 2}+c.\]
Since \(Q(0)=10\) and \(u=(t+100)Q\), Equation \ref{eq:3.10.26} implies that\[(100)(10) = {(100)^2\over 2}+c,\nonumber\]
so\[c=100(10)-{(100)^2\over 2} =-4000\nonumber\]
and therefore\[u = {(t+100)^2\over 2} -4000.\nonumber\]
Hence,\[Q = {u\over t+200}= {t+100\over 2}-{4000\over t+100}.\nonumber\]
Now let \(K(t)\) be the concentration of salt at time \(t\). Then\[K(t) = {1\over 4}-{2000\over(t+100)^2}\nonumber\]
This is shown in Figure \(\PageIndex{9}\).