Test (Final) (Mock Exam)
- Page ID
- 26376
These mock exams are provided to help you prepare for Term/Final tests. The best way to use these practice tests is to try the problems as if you are taking the test. Please don't look at the solution until you have attempted the question(s). Only reading through the solutions or studying them, will typically not be helpful in preparing since it is too easy to convince yourself that you understand it.
Let be the region \(R\), bounded by \(y=x-x^2\) and \(y=0\). Sketch the region \(R\), and then, find
- the volume of the solid generated by rotating the region \(R\) about the \(x-\)axis.
- the volume of the solid generated by rotating the region \(R\) about the line \(x=-1\).
[You may use either Washer or Shell methods.]
- Answer
-
\(\displaystyle \frac{\pi}{30} \text{Unit}^3\)
\(\displaystyle \frac{\pi}{2} \text{Unit}^3\)
- Solution
-

The intersecting points: \(x-x^2=0 \implies x(1-x)=0 \implies x=0,\) or \(x=1\).
1. By using the disc method we have, \begin{align*} V & =\pi \int_0^1 (x-x^2)^2 dx\\ &= \pi \int_0^1 (x^2-2x^3+x^4) dx\\ &= \pi \displaystyle \left. \left(\frac{x^3}{3}-2\left(\frac {x^4}{4}\right)+\frac{x^5}{5}\right) \right|_0^1 \\ &= \pi \displaystyle \left(\frac{1^3}{3}-2\left(\frac {1^4}{4}\right)+\frac{1^5}{5} \right) \\&= \displaystyle \frac{\pi}{30} \text{Unit}^3\\ \end{align*}
2. By using cylindrical shells,
\begin{align*} V & =2\pi \int_0^1 (x+1)(x-x^2) dx\\ &=2 \pi \int_0^1(-x^3+x)dx\\ &=2 \pi \displaystyle \left.\left(-\frac{x^4}{4}+\frac{x^2}{2} \right) \right|_0^1\\ &= 2\pi \displaystyle \left(-\frac{1^4}{4}+\frac{1^2}{2} \right) \\&= \displaystyle \frac{\pi}{2} \text{Unit}^3 \ \end{align*}
Find the exact arc length of the curve \(y=x^{3/2}\) from \(x=0\) to \(x=4.\)
- Answer
-
\(\displaystyle\frac{8({10}^{3/2}-1)}{27}\text{Unit}\)
- Solution
-
\(y=x^{3/2} \implies y^{\prime} =\frac{3}{2}x^{1/2}.\)
Hence \(1+ ( y^{\prime})^2 =1+(\frac{3}{2}x^{1/2})^2= 1+ \frac{9}{4}x.\)
Arc length\(= \displaystyle \int_0^4 \sqrt{1+ \frac{9}{4}x} \,dx.\)
Let \(u= \displaystyle 1+ \frac{9}{4}x, du= \displaystyle \frac{9}{4} dx.\)
\(x=0 \implies u=1\) and \(x=0 \implies u= \displaystyle 1+ \frac{9}{4}(4)=10\).
Arc length\(= \displaystyle \int_1^{10} \displaystyle \sqrt{u}\left( \frac{4}{9}du\right)= \displaystyle \left.\frac{4}{9} \frac{u^{3/2}}{3/2}\right|_1^{10}= \displaystyle \frac{8}{27}\left( {10}^{3/2}-1^{3/2}\right)= \displaystyle\frac{8({10}^{3/2}-1)}{27}\text{Unit}\).
Consider the curve \(y=\ln x, 1 \leq x \leq e\). Sketch the region and set up the integrals that give the surface areas of the surfaces generated when the region is rotated about:
- \(x\)-axis
- \(y\)-axis
[NOTE: You do not have to find the surface area, i.e do not evaluate the integrals.]
- Answer
-
1.\( 2\pi \displaystyle \int^{e}_{1} \displaystyle \frac{\ln(x)}{x} \sqrt{x^2+1} \,dx\)
2. \(2\pi \displaystyle \int_{\ln(1)}^{1} e^y \sqrt{1+e^{2y}}\, dy\)
- Solution
-
1. Let \(f(x) =\ln(x).\) Then \(f^{\prime}(x)=\displaystyle \frac{1}{x}. \) Hence \(1+[f^{\prime}(x)]^2=1+\left(\displaystyle \frac{1}{x}\right)^2= \displaystyle \frac{x^2+1}{x^2}.\)
\begin{align*} \text{Surface area} &= \displaystyle \int^b_a 2\pi f(x) \sqrt{1+[f^{\prime}(x)]^2}\,dx \\[5pt] &= \displaystyle \int^{e}_{1} 2\pi \ln(x) \sqrt{\left(\displaystyle \frac{x^2+1}{x^2} \right)}\,dx \\[5pt] &= \displaystyle 2\pi \int^{e}_{1} \displaystyle \frac{\ln(x)}{x} \sqrt{x^2+1} \,dx \end{align*}
2. Since \(y=\ln(x), x=e^y,\) and \(\ln(1) \leq y \leq 1\). Let \(g(y)=e^y.\) Then \( g^{\prime}(y)= e^y.\) \(1+[g^{\prime}(x)]^2=1+e^{2y}.\)
\begin{align*} \text{Surface area} &= \displaystyle \int^b_a 2\pi g(y) \sqrt{1+[g^{\prime}(y)]^2}\,dy \\[5pt] &= \displaystyle \int_{\ln(1)}^{1} 2\pi e^y \sqrt{1+e^{2y}} \,dy\\[5pt] &= \displaystyle 2\pi \int_{\ln(1)}^{1} e^y \sqrt{1+e^{2y}}\, dy \end{align*}
Find the mass of a thin bar with the density function: $$\rho(x)=\sqrt{9-x^2},\;\;\; 0\leq x\leq 3.$$
- Answer
-
\(\displaystyle \frac{9\pi}{4}\)
- Solution
-
Mass \(= \displaystyle \int^3_0 \sqrt{9-x^2}\;\;\; dx\)
Let \(x=3 \sin(\theta) .\) Then \(dx= 3 \cos(\theta) \;\;\; d\theta, \) and \(9-x^2=9(1- \sin^2(\theta))=9 \cos^2(\theta).\)
When \(x=0 \implies \theta=0,\) and \(x=3 \implies \theta=\frac{\pi}{2}.\)
Since \( 0 \leq \theta \leq \frac{\pi}{2} \), \(\sqrt{9 \cos^2(\theta)}=|3 \cos(\theta)|=3 \cos(\theta).\)
Hence,
\begin{align*} \text{mass} &= \displaystyle \int^{\frac{\pi}{2}}_0 3 \cos(\theta) 3 \cos(\theta) \;\;\; d\theta \\[5pt] &=9 \displaystyle \int^{\frac{\pi}{2}}_0 \cos^2(\theta) \;\;\; d\theta \\[5pt] &=\frac{9}{2} \displaystyle \int^{\frac{\pi}{2}}_0 ( \cos(2\theta)+1) \;\;\; d\theta \\[5pt] &=\left.\frac{9}{2}\left(\displaystyle \frac{\sin(2\theta)}{2}+\theta \right) \displaystyle \right|^{\frac{\pi}{2}}_0 \\[5pt] &=\frac{9}{2} \left( \displaystyle \frac{\sin(\pi)}{2} + \displaystyle \frac{\pi}{2}\right) =\displaystyle \frac{9\pi}{4}\end{align*}
Evaluate the following integrals.
- \(\displaystyle \int 4e^{x}\;\cos (3x )\; dx\)
- \(\displaystyle \int_1^e x^5 \ln x \; dx\)
- \(\displaystyle \int_0^{\pi/2} \cos^3(2x) \; dx\)
- \(\displaystyle \int \frac{1}{(1-x^2)^{3/2} } \; dx\)
- \(\displaystyle \int \frac{4x^2-4x-1}{x^3-x^2} \; dx\)
- Answer
-
1. \( \displaystyle \frac{ 3e^x\, \sin(3x)}{2} +\displaystyle \frac{ e^x\, \cos(3x)}{2}.\)
2.\(\displaystyle \frac{5e^{6}+1}{36}.\)
3. \(0.\)
4. \(\displaystyle \frac{x}{1-x^2}+C\).
5. \(5\ln|x|- \displaystyle \frac{1}{x}-\ln|x-1|+C.\)
- Solution
-
1. Integration by parts: \(u=e^x\) and \(dv=\cos (3x )\; dx.\) Then \(du=e^x \; dx,\) and \(v=\displaystyle \frac{\sin(3x)}{3}.\)
\(\displaystyle \int 4e^{x}\;\cos (3x )\; dx=4 \left( \displaystyle \frac{ e^x\, \sin(3x)}{3} -\displaystyle \int \displaystyle \frac{\sin(3x)}{3} e^x \; dx \right)=4\left( \displaystyle \frac{ e^x\, \sin(3x)}{3} -\displaystyle \frac{1}{3} \int \sin(3x) e^x \; dx \right)\)
Consider \(\displaystyle \int \sin(3x) e^x \; dx\). Integration by parts: \(u=e^x\) and \(dv=\sin (3x )\; dx.\) Then \(du=e^x \; dx,\) and \(v=\displaystyle \frac{-\cos(3x)}{3}.\)
\(\displaystyle \int \sin(3x) e^x \; dx=\displaystyle \frac{ -e^x\, \cos(3x)}{3} +\displaystyle \frac{1}{3} \int \cos(3x) e^x \; dx. \)
Now, \(\displaystyle \int 4e^{x}\;\cos (3x )\; dx=4\left( \displaystyle \frac{ e^x\, \sin(3x)}{3} -\displaystyle \frac{1}{3}\left(\displaystyle \frac{ -e^x\, \cos(3x)}{3} +\displaystyle \frac{1}{3} \int \cos(3x) e^x \; dx \right) \right). \)
\(\displaystyle \int 4e^{x}\;\cos (3x )\; dx=\displaystyle \frac{ 4 e^x\, \sin(3x)}{3} +\displaystyle \frac{4}{3}\displaystyle \frac{ e^x\, \cos(3x)}{3} +\displaystyle \frac{4}{9} \int \cos(3x) e^x \; dx . \)
Hence, \(\displaystyle \left(1- \frac{1}{9}\right) \int 4e^{x}\;\cos (3x )\; dx=\displaystyle \frac{ 4 e^x\, \sin(3x)}{3} +\displaystyle \frac{ 4e^x\, \cos(3x)}{9}.\) Thus \(\displaystyle \int 4e^{x}\;\cos (3x )\; dx=\displaystyle \frac{ 3e^x\, \sin(3x)}{2} +\displaystyle \frac{ e^x\, \cos(3x)}{2}.\)
2. Integration by parts: \(u=\ln(x)\) and \(dv=x^5\; dx.\) Then \(du=\displaystyle \frac{1}{x} \; dx,\) and \(v=\displaystyle \frac{x^6}{6}.\)
\(\displaystyle \int_1^e x^5 \ln x \; dx = \left. \displaystyle \frac{x^6}{6} \ln(x) \right|_1^e -\displaystyle \int_1^e \displaystyle \frac{x^6}{6}\frac{1}{x} \; dx = \displaystyle \frac{e^6}{6} -\displaystyle \int_1^e \displaystyle \frac{x^{5}}{6}\; dx = \displaystyle \frac{e^6}{6}- \left.\displaystyle \frac{x^{6}}{36} \right|_1^e = \displaystyle \frac{e^6}{6}- \displaystyle \frac{1}{36}+ \displaystyle \frac{e^{6}}{36}= \displaystyle \frac{5e^{6}+1}{36}.\)
3. By reduction formula: \(\displaystyle \int_0^{\pi/2} \cos^3(2x) \; dx = \left. \displaystyle \frac{1}{2} \left(\displaystyle \frac{1}{3} \cos^2(2x) \sin(2x) \right|_0^{\pi/2}+ \displaystyle \frac{2}{3} \displaystyle \int_0^{\pi/2} \cos(2x) \; dx \right) = \left. \displaystyle \frac{1}{2} \left(\displaystyle \frac{1}{3} \cos^2(2x) \sin(2x) \right|_0^{\pi/2}+ \left. \displaystyle \frac{2}{3} \displaystyle \frac{\sin(2x) }{2}\right|_0^{\pi/2} \right) = 0. \)
4. Let \(x=\sin(u)\), then \(dx=\cos(u) du\) and \((1-x^2)=\cos^2(x).\)
Hence \(\displaystyle \int \frac{1}{(1-x^2)^{3/2} } \; dx = \displaystyle \int \frac{1}{\cos^3(u)} \cos(u) \, du= \displaystyle \int \sec^2(u) \, du= \tan(u) +C.\)
Since \(x=\sin(u)\), \(tan(u)= \displaystyle \frac{x}{\sqrt{1-x^2}}\). Thus, \(\displaystyle \int \frac{1}{(1-x^2)^{3/2} } \; dx =\displaystyle \frac{x}\sqrt
(click for details)+C\).Callstack: at (Courses/Mount_Royal_University/MATH_2200:_Calculus_for_Scientists_II/Mock_Exams_(Celebration_of_Learning)/Test_(Final)_(Mock_Exam)), /content/body/section[5]/div/dl/dd[2]/p[16]/span, line 1, column 45. By partial fraction decomposition:
\(\displaystyle \frac{4x^2-4x-1}{x^3-x^2} =\displaystyle \frac{4x^2-4x-1}{x^2(x-1)}=\displaystyle\frac{A}{x}+\displaystyle \frac{B}{x^2}+\displaystyle \frac{C}{(x-1)}.\)
Hence, \( 4x^2-4x-1= Ax(x-1)+B(x-1)+Cx^2\).
By substituting \(x=0\), we get \(B=1\).
By substituting \(x=1\), we get \(C=-1\).
Since \(4=A+C\)(by comparing coefficients of \(x^2\)), \(A=5.\) Or by substituting \(x=-1\), we get \(7=2A-2B+C\). Thus \(A=5\).
Thus, \(\displaystyle \frac{4x^2-4x-1}{x^3-x^2} =\displaystyle \frac{5}{x}+ \displaystyle \frac{1}{x^2}- \displaystyle \frac{1}{(x-1)}.\)
\(\displaystyle \int \frac{4x^2-4x-1}{x^3-x^2} \; dx= \displaystyle \int \frac{5}{x} \; dx +\int \frac{1}{x^2} \; dx -\int \frac{1}{(x-1)} \; dx = 5\ln|x|- \displaystyle \frac{1}{x}-\ln|x-1|+C.\)
- Find the area of the region between the \(x\)-axis and the curve \(y=e^{-8x}\) for \(x \geq 0.\)
- Explain why \( \displaystyle \int_0^1 \ln(x) dx\) is improper. Evaluate the integral if possible. If it diverges, show that it diverges.
- Answer
-
1. \(\displaystyle \frac{1}{8}\)
2. \( \displaystyle\frac{1}{2}\)
- Solution
-
1. \begin{align*} \displaystyle \int_0^{\infty} e^{-8x}\; dx & =\lim_{b\to \infty} \displaystyle \int_0^{b} e^{-8x}\; dx\\&= \left.\lim_{b\to \infty} \displaystyle \frac{ e^{-8x}}{-8} \right|_0^{b}\\&= \lim_{b\to \infty} \left(\displaystyle \frac{ e^{-8b}}{-8}+\displaystyle \frac{1}{8} \right) \\&= \displaystyle \frac{1}{8}. \end{align*}
2. Since \(\ln(x)\) is not continuous at \(x=0\), \(\displaystyle \int_0^1 \ln(x) dx = \lim_{a \to 0^+} \displaystyle \int_a^1 \ln(x) dx.\)
Using integration by parts, \(u=\ln(x)\) and \(dv=dx\). Then \(du=\frac{1}{x}\) and \(v=x.\)
\begin{align*}\displaystyle \int_0^1 \ln(x) dx &= \lim_{a \to 0^+} \displaystyle \int_a^1 \ln(x) dx.\\ &= \left. \lim_{a \to 0^+} \left( x \ln(x) \right|_a^1- \displaystyle \int_a^1 x \, dx \right) \\&= \left. \lim_{a \to 0^+} \left( a\ln(a)- \displaystyle\frac{x^2}{2}\right|_a^1\right)\\&= \lim_{a \to 0^+} \left( a\ln(a) - \displaystyle\frac{a^2}{2} + \displaystyle\frac{1}{2}\right)\\ \end{align*}
Consider \begin{align*} \lim_{a \to 0^+} a\ln(a) &=[0.(-\infty)]\\ &= \lim_{a \to 0^+} \displaystyle\frac{ \ln(a)}{1/a} \\ &= \lim_{a \to 0^+} \displaystyle\frac{ 1/a}{-1/a^2} \text{(by L'H}\hat{o}\text{pital's rule)} \\ &= \lim_{a \to 0^+} -a=0, \\ \end{align*}
and \( \lim_{a \to 0^+} \displaystyle\frac{a^2}{2}=0.\)
Hence, \( \displaystyle \int_0^1 \ln(x) dx = \displaystyle\frac{1}{2}.\) Thus, \( \displaystyle \int_0^1 \ln(x) dx\) converges to \( \displaystyle\frac{1}{2}.\)
Solve the following initial value problems:
- \( \displaystyle x \frac{dy}{dx}=y(y+1), y(3)=1\)
- \( \displaystyle \frac{dy}{dt}+\frac{2t}{t^2+1}y(t)=1+3t^2, y(1)=4\)
- Answer
-
1.\(y=\displaystyle \frac{e^{(x-3)}}{2-e^{(x-3)}}.\)
2. \( y = (t^2+1)\left(\displaystyle \frac{3t^5}{5}+ \displaystyle \frac{4t^3}{3}+t-\displaystyle \frac{14}{15}\right).\)
- Solution
-
1. \begin{align*}\displaystyle x \frac{dy}{dx}& = y(y+1)\\ \displaystyle \int \frac{dy}{y(y+1)}& = \displaystyle \int\frac{dx}{x}\\ \displaystyle \int \left(\frac{dy}{y}- \frac{dy}{y+1}\right)& =ln(x)+C\\ \ln|y|-ln|y+1|& =ln(x)+C\\ \ln\left|\displaystyle \frac{y}{y+1}\right| & =ln(x)+C\\ \displaystyle \frac{y}{y+1}&= Ae^x\\ \end{align*}
\(x=3\) and \(y=1, \implies \frac{1}{2}= Ae^3.\) Thus \(A= \frac{e^{-3}}{2}\).
Hence \(\displaystyle \frac{y}{y+1}= \displaystyle \frac{e^{-3}}{2}e^x =\displaystyle \frac{e^{x-3}}{2}.\) Therefore, \(y=\displaystyle \frac{e^{(x-3)}}{2-e^{(x-3)}}.\)
2. Integrating factor \(= \displaystyle e^{\int \frac{2t}{t^2+1}\, dt}= e^{ln(t^2+1)}= t^2+1.\)
Multiply both sides by \(t^2+1\), we get
\( \displaystyle (t^2+1) \frac{dy}{dt}+2ty(t)=(1+3t^2) (t^2+1)\)
Now, \( \displaystyle \frac{d((t^2+1)y)}{dt}=(1+3t^2) (t^2+1)=3t^4+4t^2+1\)
\begin{align*} \displaystyle \int d((t^2+1)y) & =\int (3t^4+4t^2+1) \,dt\\ (t^2+1)y & = \displaystyle \frac{3t^5}{5}+ \displaystyle \frac{4t^3}{3}+t+C\\ y & = (t^2+1)\left(\displaystyle \frac{3t^5}{5}+ \displaystyle \frac{4t^3}{3}+t+C\right).\\ \end{align*}
When \(t=1, y=4 \implies 4=(1^2+1)\left(\displaystyle \frac{3}{5}+ \displaystyle \frac{4}{3}+1+C\right).\)
Hence,\( C=2-\left(\displaystyle \frac{3}{5}+ \displaystyle \frac{4}{3}+1\right)= \displaystyle \frac{-14}{15}.\)
Thus, \( y = (t^2+1)\left(\displaystyle \frac{3t^5}{5}+ \displaystyle \frac{4t^3}{3}+t-\displaystyle \frac{14}{15}\right).\)
Use an appropriate test to determine if the following series converges or diverges. Justify your answer.
- \( \sum_{k=2}^{\infty} \displaystyle \frac{k}{k^2-1}\)
- \( \sum_{k=1}^{\infty} \displaystyle \frac{5^k}{2(k!)}\)
- \( \sum_{k=2}^{\infty} \displaystyle \frac{(-1)^k}{\sqrt{k+2}}\)
- Answer
-
1. diverges.
2. converges.
3. converges.
- Solution
-
1. Since \(k^2 \geq (k^2-1)\) for all \(k \geq 2, \displaystyle \frac{1}{k^2} \leq \displaystyle \frac{1}{(k^2-1)},\) for all \(k \geq 2\). Thus \(\displaystyle \frac{k}{k^2}= \displaystyle \frac{1}{k}\leq \displaystyle \frac{k}{k^2-1},\) for all \(k \geq 2\). Since \(\sum_{k=2}^\infty \dfrac{1}{ k}\) is harmonic series and it diverges, by comparison test, \( \sum_{k=2}^{\infty} \displaystyle \frac{k}{k^2-1}\) diverges.
2. Let \(a_k=\displaystyle \frac{5^k}{2(k!)}\). By using the Ratio test, we have
\begin{align*} \rho &= \lim_{k\to\infty} \displaystyle \frac{\left(\displaystyle \frac{5^{(k+1)}}{2(k+1)!)}\right)}{\left(\displaystyle \frac{5^k}{2(k!)}\right)}\\ &\\ &=\lim_{k\to\infty} \displaystyle \frac{5^{(k+1)}(k!)}{5^k(k+1)!}\\ &\\ &=\lim_{k\to\infty} \displaystyle \frac{5}{(k+1)}=0 <1.\\ \end{align*}
Bythe Ratio test, \( \sum_{k=1}^{\infty} \displaystyle \frac{5^k}{2(k!)}\) converges.
3. Let \(a_k=\displaystyle \frac{1}{\sqrt{k+2}}.\) Notice that \(0 \geq a_{k+1} \geq a_k \) and \( \lim_{k \to \infty} a_k=0.\) Hence by the alternating series test \( \sum_{k=2}^{\infty} \displaystyle \frac{(-1)^k}{\sqrt{k+2}}\) converges.
Find the radius of convergence and the interval of convergence of
$$\sum_{k=0}^\infty (-3)^k {x^{k+1}\over k+1} \nonumber$$
- Answer
-
The radius of convergence of the series is \( \dfrac{1}{3},\) and the interval of convergence is \((-\dfrac{1}{3}, \dfrac{1}{3}].\)
- Solution
-
Here \(a_k =(-3)^k {x^{k+1}\over k+1},\) so
\begin{align*}\rho & = \lim_{k\to\infty}\left|a_{k+1}\over a_k\right|\\&=\lim_{k\to\infty} \dfrac{\left|(-3)^{k+1} {x^{k+2}\over k+2} \right|}{\left|(-3)^k {x^{k+1}\over k+1} \right|}\\&= |x| \lim_{k\to\infty} \dfrac{3(k+1)}{(k+2)}\\&= 3|x|\end{align*}
Hence by the Ratio test, the series converges absolutely when \(3|x| <1\) and it diverges when \(3|x|>1.\) Thus, the series converges when \(|x| <\dfrac{1}{3}\) and it diverges when \(3|x|>\dfrac{1}{3}.\)
Therefore, the radius of convergence of the series is \( \dfrac{1}{3},\) and the open interval of convergence is \((-\dfrac{1}{3}, \dfrac{1}{3}).\)
Let's check the endpoints!
Suppose \(x=\dfrac{1}{3}.\) Then the series is $$\sum_{k=0}^\infty (-3)^k {\left(\dfrac{1}{3}\right)^{k+1}\over k+1}= \sum_{k=0}^\infty (-1)^k \dfrac{1}{3}\dfrac{1}{ k+1} \nonumber$$
Since \( \sum_{k=0}^\infty (-1)^k \dfrac{1}{ k+1}\) is an alternating harmonic series and it converges, \( \sum_{k=0}^\infty (-1)^k \dfrac{1}{3}\dfrac{1}{( k+1)}\) converges.
Suppose \(x=\dfrac{-1}{3}.\) Then the series is $$\sum_{k=0}^\infty (-3)^k {\left(\dfrac{-1}{3}\right)^{k+1}\over k+1}= \sum_{k=0}^\infty \dfrac{1}{3}\dfrac{1}{ (k+1)} \nonumber$$
Since \(\sum_{k=0}^\infty \dfrac{1}{ k+1}\) is harmonic series and it diverges, \( \sum_{k=0}^\infty (-1)^k \dfrac{1}{3}\dfrac{1}{( k+1)}\) diverges.
Hence the interval of convergence is \((-\dfrac{1}{3}, \dfrac{1}{3}].\)
Consider the function \(\displaystyle f(x)= ln(x).\)
- Find the third order Taylor polynomial of \(\displaystyle f(x)\) about \(x=1.\)
- Write the Taylor Series for \(f(x)\) about \(x=1\) in sigma notation.
- Answer
-
- \((x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3\)
- \(\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\left(x-1\right)^n\)
- Solution
-
To find these Taylor polynomials, we need to evaluate \(f\) and its first three derivatives at \(x=1\).
\[\begin{align*} f(x)&=\ln x & f(1)&=0\\[5pt]
f′(x)&=\dfrac{1}{x} & f′(1)&=1\\[5pt]
f''(x)&=−\dfrac{1}{x^2} & f''(1)&=−1\\[5pt]
f'''(x)&=\dfrac{2}{x^3} & f'''(1)&=2\end{align*}\]Therefore,
\[\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}\] Hence, the Taylor series about \(x=1\) is \(\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\left(x-1\right)^n.\)
Consider the function \(\displaystyle f(x,y)=2+\sin(xy) .\)
- Find all the first partial derivatives of the function \(f(x,y)\)
- Verify that the second partial derivatives \(f_{xy}=f_{yx}, \) for the function \(f(x,y)\).
- Answer
-
- \(\displaystyle \frac{\partial f}{\partial x}=y \cos(xy)\),and \(\displaystyle \frac{\partial f}{\partial y}=x\cos(xy).\)
- Solution
-
1. \(\displaystyle \frac{\partial f}{\partial x}=y \cos(xy)\),and \(\displaystyle \frac{\partial f}{\partial y}=x\cos(xy)\)
2. \(\displaystyle \frac{\partial^2 f}{\partial x \partial y}= \cos(xy)-xy\sin(xy) \),and \(\displaystyle \frac{\partial f}{\partial y \partial x}=\cos(xy)-y \sinThanks for sharing(xy)\). Hence \(f_{xy}=f_{yx}. \)
- Evaluate \(\int \int_R y^2 dA\) where \(R\) is the region bounded by \(y=2x+2,x=1\), and \(y=-x-1.\)
- Evaluate the integral by first reversing the order of integration \(\displaystyle \int_{0}^{\pi/2} \int_{y}^{\pi/2} \frac{\sin x}{x} \, dx dy\)
- Use a double integral in polar coordinates to find the volume of the solid bounded by the paraboloid \(z=x^2+y^2\) and \(z=6-x^2-y^2.\)
- Answer
-
- \(12\)
- \(1\)
- 3. \(9\pi\) unit\(^3\).
- Solution
-
1.
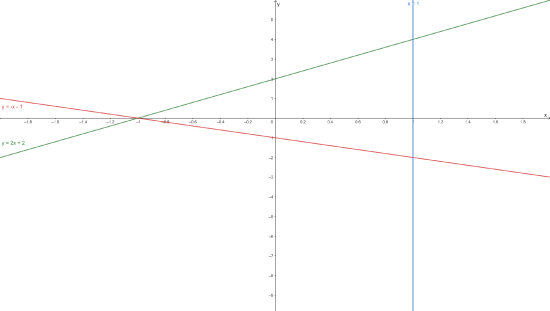
\begin{align*} \displaystyle \int \int_R y^2 dA &= \displaystyle \int_{-1}^{1} \int_{-x-1}^{2x+2} y^2\, dydx\\ &= \left.\displaystyle \int_{-1}^{1} \frac{y^3}{3}\right|_{-x-1}^{2x+2} \, dx\\ &= \displaystyle \int_{-1}^{1} \left(\frac{(2x+2)^3}{3}- \frac{(-x-1)^3}{3}\right) \, dx\\ &= \displaystyle \int_{-1}^{1} \left(8\frac{(x+1)^3}{3}+ \frac{(x+1)^3}{3}\right) \, dx\\ &= \displaystyle \int_{-1}^{1} 3(x+1)^3 \, dx \\ &= \left. 3 \displaystyle \frac{(x+1)^4}{4}\right|_{-1}^{1} \\ &=3 \displaystyle \frac{2^4}{4} = 12.\\ \end{align*}
2.
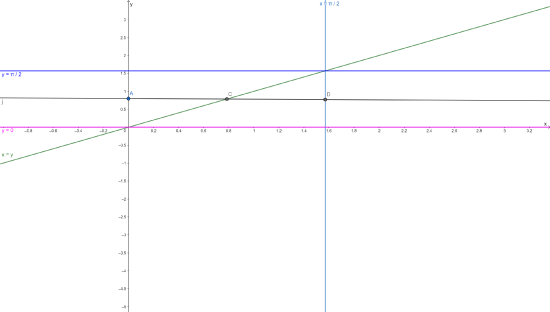
\begin{align*}\displaystyle \int_{0}^{\pi/2} \int_{y}^{\pi/2} \frac{\sin (x)}{x} \, dx dy &= \displaystyle \displaystyle \int_{0}^{\pi/2} \int_{0}^{x} \frac{\sin(x)}{x} \, dy dx\\ &= \left.\displaystyle \int_{0}^{\pi/2} \frac{\sin x}{x}y\right|_{0}^{x} \, dx\\ &= \displaystyle \int_{0}^{\pi/2} \frac{\sin x}{x}x \, dx\\ &= \displaystyle \int_{0}^{\pi/2} \sin x\, dx\\ &= -\left. \cos(x)\right|_{0}^{\pi/2} \\ &= 1.\\ \end{align*}
3.
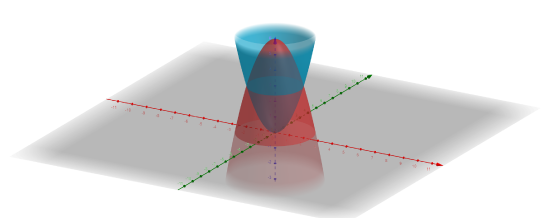
Intersections: \(x^2+y^2=6-x^2-y^2 \implies x^2+y^2=3.\) Using polar coordinates, \( x=r \cos(\theta), y=r \sin(\theta), r^2=x^2+y^2.\)
Hence, \( 0\leq r \leq \sqrt{3}\) and \(0 \leq \theta \leq 2 \pi.\)
\begin{align*} Volume &= \displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}}((6-x^2-y^2)-(x^2+y^2)) r\, dr \,d\theta\\&= \displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}}(6-2x^2-2y^2) r\, dr \,d\theta \\&= \displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}}(6-2r^2) r\, dr \,d\theta \\&= \displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}}(6r-2r^3) \, dr \,d\theta \\&= \left.\displaystyle \int_{0}^{2\pi}\left( \displaystyle \frac{6r^2}{2}-\displaystyle \frac{2r^4}{4} \right)\right|_{0}^{\sqrt{3}}\,d\theta \\&= \left.\displaystyle \frac{9}{2} \theta \right|_{0}^{2\pi} = 9 \pi \text{unit}^3.\\ \end{align*}
The function \(P(t)\) represents the population of a particular organism as a function of time \(t\), and the constant \(P_0\) represents the initial population (population of the organism at time \(t=0\)). Then the logistic differential equation is \[\dfrac{dP}{dt}=rP\left(1-\dfrac{P}{K}\right),\]where \(K\) represent the carrying capacity for the organism in a given environment, and let \(r\) be a real number that represents the growth rate.
Initially, there were \(10\) prairie dogs; after one year the population reaches \(20\) prairie dogs. After a few years, the population has leveled out at approximately \(200\) prairie dogs. Assuming that a logistic growth model applies to this community,
- Set up and solve the initial value problem.
- Find a function that models the population.
- Solution
-
1. The initial value problem is
\[ \dfrac{dP}{dt}=rP \left(1−\dfrac{P}{200}\right),\,\,P(0)=10, P(1)=20. \nonumber\]
\[ \begin{align*} \dfrac{dP}{dt} =rP\left(\dfrac{200−P}{200} \right) \\[4pt] dP =rP\left(\dfrac{200−P}{200}\right)dt \\[4pt] \dfrac{dP}{P(200−P)} =\dfrac{r}{200}dt. \end{align*}\]
\[\begin{align*} \int \dfrac{dP}{P(200−P)}& =\int \dfrac{dP}{200P)} - \int\dfrac{dP}{200(200−P)}=\dfrac{r}{200}dt \\[4pt] \dfrac{1}{200}\left(\ln |P|−\ln |200−P|\right) =\dfrac{rt}{200} +C \\[4pt] \dfrac{1}{200}\ln\left|\dfrac{P}{200-P}\right| =\dfrac{rt}{200} +C \\[4pt] \ln\left|\dfrac{P}{200-P}\right| =rt+C\\ \dfrac{P}{200-P}=e^{rt+C}=Ae^{rt}.\\ \end{align*}\]
Since \(P(0)=10, \dfrac{10}{200-10} =A \implies A= \dfrac{1}{21}.\)
Thus \(\dfrac{P}{200-P} =\dfrac{1}{21}e^{rt} \implies P= \dfrac{1}{21}e^{rt}(200-P) .\)
\( \left( 1+\dfrac{1}{21}e^{rt}\right) P= \dfrac{200}{21}e^{rt} \)
\( P= \dfrac{\dfrac{200}{21}e^{rt}} {\left( 1+\dfrac{1}{21}e^{rt}\right)}= \dfrac{200}{21 e^{-rt}+1}\)
Since \(P(1)=20, 20=\dfrac{200}{21 e^{-r}+1} \implies (21 e^{-r}+1)=10 \implies e^{-r}=\dfrac{3}{7}.\)
Thus \(r=-\ln \left(\dfrac{3}{7}\right).\)
Hence \(P=\dfrac{200}{21 e^{\ln \left(\dfrac{3}{7}\right)t}+1}= \dfrac{200}{21 \left(\dfrac{3}{7}\right)^t+1}.\)


