Chapter 2

Last updated
Save as PDF

Page ID: 34378

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercise $\PageIndex{1}$

Solutions Exercises 2.1

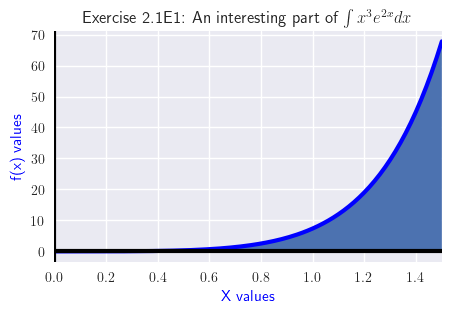
Exercise 2.1E1

Hint:

$ Let \hspace{5mm} u = x^{3} $

Table of integration and initial equation:

$ \begin{array}{r|r} \nonumber Let \hspace{1mm} u=x^{3} & Let \hspace{1mm} dv = e^{2 x}dx \\ du = 3 x^{2}dx & v = \frac{e^{2 x}}{2}\end{array} $
$ \int x^{3} e^{2 x}\, dx = \frac{x^{3} e^{2 x}}{2} - \int \frac{3 x^{2} e^{2 x}}{2}\, dx $

Antiderivative and graph snippet:

$ \int x^{3} e^{2 x}\, dx = \frac{\left(4 x^{3} - 6 x^{2} + 6 x - 3\right) e^{2 x}}{8} + C $

$Exercise 2.1E1.png$

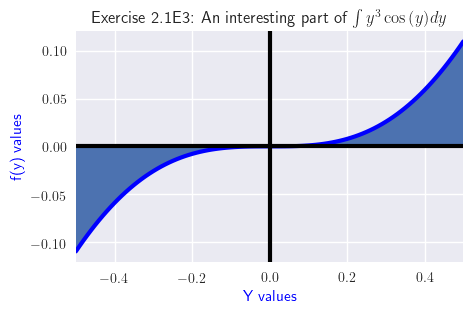
Exercise 2.1E3

Hint:

$ Let \hspace{5mm} u = y^{3} $

Table of integration and initial equation:

$ \begin{array}{r|r} \nonumber Let \hspace{1mm} u=y^{3} & Let \hspace{1mm} dv = \cos{\left(y \right)}dy \\ du = 3 y^{2}dy & v = \sin{\left(y \right)}\end{array} $
$ \int y^{3} \cos{\left(y \right)}\, dy = y^{3} \sin{\left(y \right)} - \int 3 y^{2} \sin{\left(y \right)}\, dy $

Antiderivative and graph snippet:

$ \int y^{3} \cos{\left(y \right)}\, dy = y^{3} \sin{\left(y \right)} + 3 y^{2} \cos{\left(y \right)} - 6 y \sin{\left(y \right)} - 6 \cos{\left(y \right)} + C $

$Exercise 2.1E3.png$

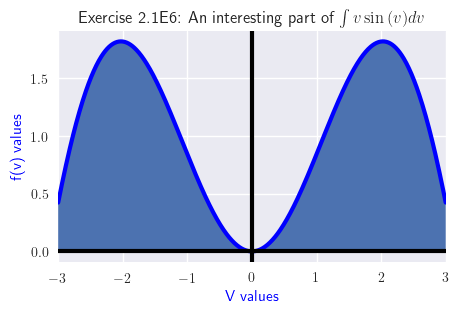
Exercise 2.1E6

Hint:

$ Let \hspace{5mm} u = v $

Table of integration and initial equation:

$ \begin{array}{r|r} \nonumber Let \hspace{1mm} u=v & Let \hspace{1mm} dv = \sin{\left(v \right)}dv \\ du = 1dv & v = - \cos{\left(v \right)}\end{array} $
$ \int v \sin{\left(v \right)}\, dv = - v \cos{\left(v \right)} - \int - \cos{\left(v \right)}\, dv $

Antiderivative and graph snippet:

$ \int v \sin{\left(v \right)}\, dv = - v \cos{\left(v \right)} + \sin{\left(v \right)} + C $

$Exercise 2.1E6.png$