2.3: Linear Second Order Nonhomogeneous Linear Equations

We'll now consider the nonhomogeneous linear second order equation

\begin{equation}\label{eq:2.3.1}
y''+p(x)y'+q(x)y=f(x),
\end{equation}

where the forcing function \(f\) isn't identically zero. The next theorem, an extension of Theorem \((2.1.1)\), gives sufficient conditions for existence and uniqueness of solutions of initial value problems for \eqref{eq:2.3.1}. We omit the proof, which is beyond the scope of this book.

Theorem \(\PageIndex{1}\)

Suppose \(p,\) \(q,\) and \(f\) are continuous on an open interval \((a,b),\) let \(x_0\) be any point in \((a,b),\) and let \(k_0\) and \(k_1\) be arbitrary real numbers. Then the initial value problem

\begin{eqnarray*}
y''+p(x)y'+q(x)y=f(x), \quad y(x_0)=k_0,\quad y'(x_0)=k_1
\end{eqnarray*}

has a unique solution on \((a,b).\)

Proof

Add proof here and it will automatically be hidden if you have a "AutoNum" template active on the page.

To find the general solution of \eqref{eq:2.3.1} on an interval \((a,b)\) where \(p\), \(q\), and \(f\) are continuous, it's necessary to find the general solution of the associated homogeneous equation

\begin{equation}\label{eq:2.3.2}
y''+p(x)y'+q(x)y=0
\end{equation}

on \((a,b)\). We call \eqref{eq:2.3.2} the \( \textcolor{blue}{\mbox{complementary equation}} \) for \eqref{eq:2.3.1}.

The next theorem shows how to find the general solution of \eqref{eq:2.3.1} if we know one solution \(y_p\) of \eqref{eq:2.3.1} and a fundamental set of solutions of \eqref{eq:2.3.2}. We call \(y_p\) a \( \textcolor{blue}{\mbox{particular solution}} \) of \eqref{eq:2.3.1}; it can be any solution that we can find, one way or another.

Theorem \(\PageIndex{2}\)

Suppose \(p,\) \(q,\) and \(f\) are continuous on \((a,b).\) Let \(y_p\) be a particular solution of

\begin{equation}\label{eq:2.3.3}
y''+p(x)y'+q(x)y=f(x)
\end{equation}

on \((a,b)\), and let \(\{y_1,y_2\}\) be a fundamental set of solutions of the complementary equation

\begin{equation}\label{eq:2.3.4}
y''+p(x)y'+q(x)y=0
\end{equation}

on \((a,b)\). Then \(y\) is a solution of \eqref{eq:2.3.3} on \((a,b)\) if and only if

\begin{equation}\label{eq:2.3.5}
y=y_p+c_1y_1+c_2y_2,
\end{equation}

where \(c_1\) and \(c_2\) are constants.

Proof

We first show that \(y\) in \eqref{eq:2.3.5} is a solution of \eqref{eq:2.3.3} for any choice of the constants \(c_1\) and \(c_2\). Differentiating \eqref{eq:2.3.5} twice yields

\begin{eqnarray*}
y'=y_p'+c_1y_1'+c_2y_2' \quad \mbox{and} \quad y''=y_p''+ c_1y_1''+c_2y_2'',
\end{eqnarray*}

so

\begin{eqnarray*}
y''+p(x)y'+q(x)y&=&(y_p''+c_1y_1''+c_2y_2'') +p(x)(y_p'+c_1y_1'+c_2y_2') +q(x)(y_p+c_1y_1+c_2y_2)\\
&=&(y_p''+p(x)y_p'+q(x)y_p)+c_1(y_1''+p(x)y_1'+q(x)y_1) +c_2(y_2''+p(x)y_2'+q(x)y_2)\\
&=& f+c_1\cdot0+c_2\cdot0=f,
\end{eqnarray*}

since \(y_p\) satisfies \eqref{eq:2.3.3} and \(y_1\) and \(y_2\) satisfy \eqref{eq:2.3.4}.

Now we'll show that every solution of \eqref{eq:2.3.3} has the form \eqref{eq:2.3.5} for some choice of the constants \(c_1\) and \(c_2\). Suppose \(y\) is a solution of \eqref{eq:2.3.3}. We'll show that \(y-y_p\) is a solution of \eqref{eq:2.3.4}, and therefore of the form \(y-y_p=c_1y_1+c_2y_2\), which implies \eqref{eq:2.3.5}. To see this, we compute

\begin{eqnarray*}
(y-y_p)''+p(x)(y-y_p)'+q(x)(y-y_p)&=&(y''-y_p'')+p(x)(y'-y_p') +q(x)(y-y_p)\\
&=&(y''+p(x)y'+q(x)y) -(y_p''+p(x)y_p'+q(x)y_p)\\
&=&f(x)-f(x)=0,
\end{eqnarray*}

since \(y\) and \(y_p\) both satisfy \eqref{eq:2.3.3}.

We say that \eqref{eq:2.3.5} is the \( \textcolor{blue}{\mbox{general solution of \(\eqref{eq:2.3.3}\) on \((a,b)\).}} \)

If \(P_0\), \(P_1\), and \(F\) are continuous and \(P_0\) has no zeros on \((a,b)\), then Theorem \((2.3.2)\) implies that the general solution of

\begin{equation}\label{eq:2.3.6}
P_0(x)y''+P_1(x)y'+P_2(x)y=F(x)
\end{equation}

on \((a,b)\) is \(y=y_p+c_1y_1+c_2y_2\), where \(y_p\) is a particular solution of \eqref{eq:2.3.6} on \((a,b)\) and \(\{y_1,y_2\}\) is a fundamental set of solutions of

\begin{eqnarray*}
P_0(x)y''+P_1(x)y'+P_2(x)y=0
\end{eqnarray*}

on \((a,b)\). To see this, we rewrite \eqref{eq:2.3.6} as

\begin{eqnarray*}
y''+{P_1(x)\over P_0(x)}y'+{P_2(x)\over P_0(x)}y={F(x)\over P_0(x)}
\end{eqnarray*}

and apply Theorem \((2.3.2)\) with \(p=P_1/P_0\), \(q=P_2/P_0\), and \(f=F/P_0\).

To avoid awkward wording in examples and exercises, we won't specify the interval \((a,b)\) when we ask for the general solution of a specific linear second order equation, or for a fundamental set of solutions of a homogeneous linear second order equation. Let's agree that this always means that we want the general solution (or a fundamental set of solutions, as the case may be) on every open interval on which \(p\), \(q\), and \(f\) are continuous if the equation is of the form \eqref{eq:2.3.3}, or on which \(P_0\), \(P_1\), \(P_2\), and \(F\) are continuous and \(P_0\) has no zeros, if the equation is of the form \eqref{eq:2.3.6}. We leave it to you to identify these intervals in specific examples and exercises.

For completeness, we point out that if \(P_0\), \(P_1\), \(P_2\), and \(F\) are all continuous on an open interval \((a,b)\), but \(P_0\) \( \textcolor{blue}{\mbox{does}} \) have a zero in \((a,b)\), then \eqref{eq:2.3.6} may fail to have a general solution on \((a,b)\) in the sense just defined. Exercises \((2.1E.42)\), \((2.1E.43)\), and \((2.1E.44)\) illustrate this point for a homogeneous equation.

In this section we limit ourselves to applications of Theorem \((2.3.2)\) where we can guess at the form of the particular solution.

Example \(\PageIndex{1}\)

(a) Find the general solution of

\begin{equation}\label{eq:2.3.7}
y''+y=1.
\end{equation}

(b) Solve the initial value problem

\begin{equation}\label{eq:2.3.8}
y''+y=1, \quad y(0)=2,\quad y'(0)=7.
\end{equation}

Answer

(a) We can apply Theorem \((2.3.2)\) with \((a,b)= (-\infty,\infty)\), since the functions \(p\equiv0\), \(q\equiv1\), and \(f\equiv1\) in \eqref{eq:2.3.7} are continuous on \((-\infty,\infty)\). By inspection we see that \(y_p\equiv1\) is a particular solution of \eqref{eq:2.3.7}. Since \(y_1=\cos x\) and \(y_2=\sin x\) form a fundamental set of solutions of the complementary equation \(y''+y=0\), the general solution of \eqref{eq:2.3.7} is

\begin{equation}\label{eq:2.3.9}
y=1+c_1\cos x+c_2\sin x.
\end{equation}

(b) Imposing the initial condition \(y(0)=2\) in \eqref{eq:2.3.9} yields \(2=1+c_1\), so \(c_1=1\). Differentiating \eqref{eq:2.3.9} yields

\begin{eqnarray*}
y'=-c_1\sin x+c_2\cos x.
\end{eqnarray*}

Imposing the initial condition \(y'(0)=7\) here yields \(c_2=7\), so the solution of \eqref{eq:2.3.8} is

\begin{eqnarray*}
y=1+\cos x+7\sin x.
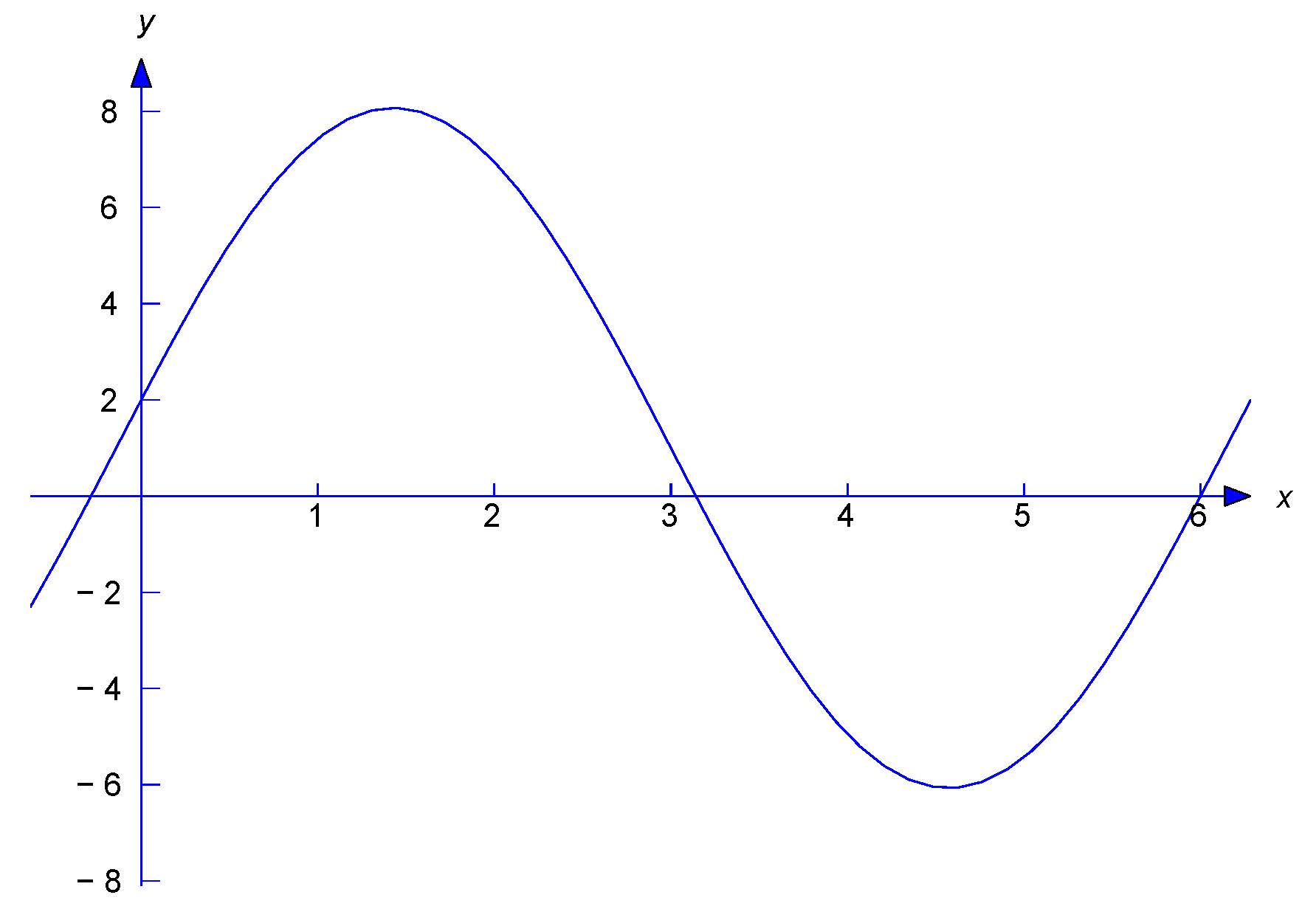
\end{eqnarray*}

Figure \(2.3.1\) is a graph of this function.

Figure: \(2.3.1\)

\(y=1+\cos x+7\sin x\)

Example \(\PageIndex{2}\)

(a) Find the general solution of

\begin{equation}\label{eq:2.3.10}
y''-2y'+y=-3-x+x^2.
\end{equation}

(b) Solve the initial value problem

\begin{equation}\label{eq:2.3.11}
y''-2y'+y=-3-x+x^2, \quad y(0)=-2,\quad y'(0)=1.
\end{equation}

Answer

(a) The characteristic polynomial of the complementary equation

\begin{eqnarray*}
y''-2y'+y=0
\end{eqnarray*}

is \(r^2-2r+1=(r-1)^2\), so \(y_1=e^x\) and \(y_2=xe^x\) form a fundamental set of solutions of the complementary equation. To guess a form for a particular solution of \eqref{eq:2.3.10}, we note that substituting a second degree polynomial \(y_p=A+Bx+Cx^2\) into the left side of \eqref{eq:2.3.10} will produce another second degree polynomial with coefficients that depend upon \(A\), \(B\), and \(C\). The trick is to choose \(A\), \(B\), and \(C\) so the polynomials on the two sides of \eqref{eq:2.3.10} have the same coefficients; thus, if

\begin{eqnarray*}
y_p=A+Bx+Cx^2 \quad \mbox{then} \quad y_p'=B+2Cx\mbox{\quad and \quad} y_p''=2C,
\end{eqnarray*}

so

\begin{eqnarray*}
y_p''-2y_p'+y_p&=&2C-2(B+2Cx)+(A+Bx+Cx^2)\\
&=&(2C-2B+A)+(-4C+B)x+Cx^2=-3-x+x^2.
\end{eqnarray*}

Equating coefficients of like powers of \(x\) on the two sides of the last equality yields

\begin{eqnarray*}
C&=&\phantom{-}1\phantom{.}\\
B-4C&=&-1\phantom{.}\\
A-2B+2C&=& -3,
\end{eqnarray*}

so \(C=1\), \(B=-1+4C=3\), and \(A=-3-2C+2B=1\). Therefore \(y_p=1+3x+x^2\) is a particular solution of \eqref{eq:2.3.10} and Theorem \((2.3.2)\) implies that

\begin{equation}\label{eq:2.3.12}
y=1+3x+x^2+e^x(c_1+c_2x)
\end{equation}

is the general solution of \eqref{eq:2.3.10}.

(b) Imposing the initial condition \(y(0)=-2\) in \eqref{eq:2.3.12} yields \(-2=1+c_1\), so \(c_1=-3\). Differentiating \eqref{eq:2.3.12} yields

\begin{eqnarray*}
y'=3+2x+e^x(c_1+c_2x)+c_2e^x,
\end{eqnarray*}

and imposing the initial condition \(y'(0)=1\) here yields \(1=3+c_1+c_2\), so \(c_2=1\). Therefore the solution of \eqref{eq:2.3.11} is

\begin{eqnarray*}
y=1+3x+x^2-e^x(3-x).
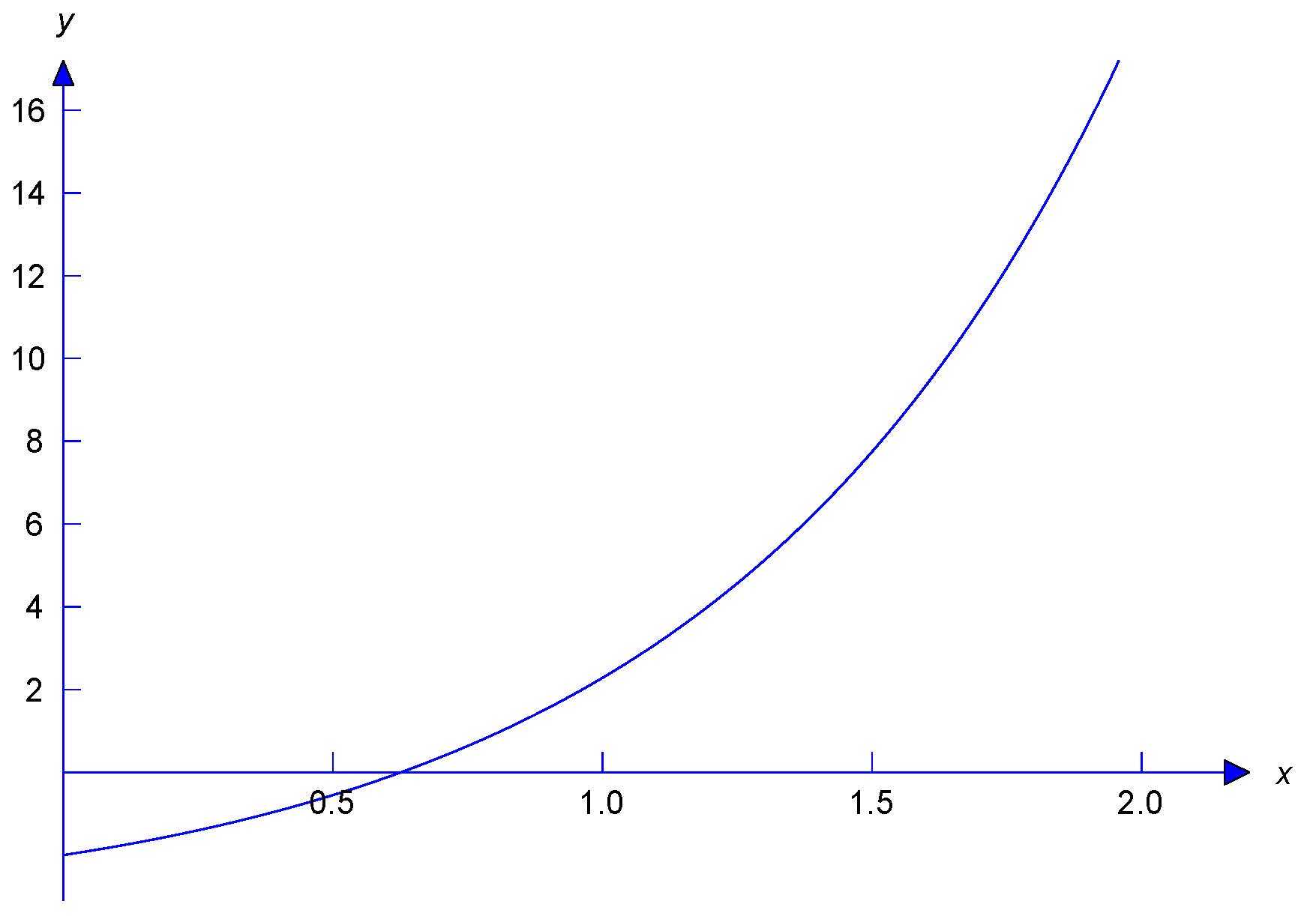
\end{eqnarray*}

Figure \(2.3.2\) is a graph of this solution.

Figure: \(2.3.2\)

\(y=1+3x+x^2-e^x(3-x)\)

Example \(\PageIndex{3}\)

Find the general solution of

\begin{equation}\label{eq:2.3.13}
x^2y''+xy'-4y=2x^4
\end{equation}

on \((-\infty,0)\) and \((0,\infty)\).

Answer

In Example \((2.3.1)\), we verified that \(y_1=x^2\) and \(y_2=1/x^2\) form a fundamental set of solutions of the complementary equation

\begin{eqnarray*}
x^2y''+xy'-4y=0
\end{eqnarray*}

on \((-\infty,0)\) and \((0,\infty)\). To find a particular solution of \eqref{eq:2.3.13}, we note that if \(y_p=Ax^4\), where \(A\) is a constant then both sides of \eqref{eq:2.3.13} will be constant multiples of \(x^4\) and we may be able to choose \(A\) so the two sides are equal. This is true in this example, since if \(y_p=Ax^4\) then

\begin{eqnarray*}
x^2y_p''+xy_p'-4y_p=x^2(12Ax^2)+x(4Ax^3)-4Ax^4=12Ax^4=2x^4
\end{eqnarray*}

if \(A=1/6\); therefore, \(y_p=x^4/6\) is a particular solution of \eqref{eq:2.3.13} on \((-\infty,\infty)\). Theorem \((2.3.2)\) implies that the general solution of \eqref{eq:2.3.13} on \((-\infty,0)\) and \((0,\infty)\) is

\begin{eqnarray*}
y={x^4\over6}+c_1x^2+{c_2\over x^2}.
\end{eqnarray*}

The Principle of Superposition

The next theorem enables us to break a nonhomogeneous equation into simpler parts, find a particular solution for each part, and then combine their solutions to obtain a particular solution of the original problem.

Theorem \(\PageIndex{3}\)

Suppose \(y_{p_1}\) is a particular solution of

\begin{eqnarray*}
y''+p(x)y'+q(x)y=f_1(x)
\end{eqnarray*}

on \((a,b)\) and \(y_{p_2}\) is a particular solution of

\begin{eqnarray*}
y''+p(x)y'+q(x)y=f_2(x)
\end{eqnarray*}

on \((a,b)\). Then

\begin{eqnarray*}
y_p=y_{p_1}+y_{p_2}
\end{eqnarray*}

is a particular solution of

\begin{eqnarray*}
y''+p(x)y'+q(x)y=f_1(x)+f_2(x)
\end{eqnarray*}

on \((a,b)\).

Proof

If \(y_p=y_{p_1}+y_{p_2}\) then

\begin{eqnarray*}
y_p''+p(x)y_p'+q(x)y_p&=&(y_{p_1}+y_{p_2})''+p(x)(y_{p_1}+y_{p_2})' +q(x)(y_{p_1}+y_{p_2})\\
&=&\left(y_{p_1}''+p(x)y_{p_1}'+q(x)y_{p_1}\right) +\left(y_{p_2}''+p(x)y_{p_2}'+q(x)y_{p_2}\right)\\
&=&f_1(x)+f_2(x).
\end{eqnarray*}

It's easy to generalize Theorem \((2.3.3)\) to the equation

\begin{equation}\label{eq:2.3.14}
y''+p(x)y'+q(x)y=f(x)
\end{equation}

where

\begin{eqnarray*}
f=f_1+f_2+\cdots+f_k;
\end{eqnarray*}

thus, if \(y_{p_i}\) is a particular solution of

\begin{eqnarray*}
y''+p(x)y'+q(x)y=f_i(x)
\end{eqnarray*}

on \((a,b)\) for \(i=1\), \(2\), \(\dots\), \(k\), then \(y_{p_1}+y_{p_2}+\cdots+y_{p_k}\) is a particular solution of \eqref{eq:2.3.14} on \((a,b)\). Moreover, by a proof similar to the proof of Theorem \((2.3.3)\) we can formulate the principle of superposition in terms of a linear equation written in the form

\begin{eqnarray*}
P_0(x)y''+P_1(x)y'+P_2(x)y=F(x)
\end{eqnarray*}

(Exercise \((2.3E.39)\)); that is, if \(y_{p_1}\) is a particular solution of

\begin{eqnarray*}
P_0(x)y''+P_1(x)y'+P_2(x)y=F_1(x)
\end{eqnarray*}

on \((a,b)\) and \(y_{p_2}\) is a particular solution of

\begin{eqnarray*}
P_0(x)y''+P_1(x)y'+P_2(x)y=F_2(x)
\end{eqnarray*}

on \((a,b)\), then \(y_{p_1}+y_{p_2}\) is a solution of

\begin{eqnarray*}
P_0(x)y''+P_1(x)y'+P_2(x)y=F_1(x)+F_2(x)
\end{eqnarray*}

on \((a,b)\).

Example \(\PageIndex{4}\)

The function \(y_{p_1}=x^4/15\) is a particular solution of

\begin{equation}\label{eq:2.3.15}
x^2y''+4xy'+2y=2x^4
\end{equation}

on \((-\infty,\infty)\) and \(y_{p_2}=x^2/3\) is a particular solution of

\begin{equation}\label{eq:2.3.16}
x^2y''+4xy'+2y=4x^2
\end{equation}

on \((-\infty,\infty)\). Use the principle of superposition to find a particular solution of

\begin{equation}\label{eq:2.3.17}
x^2y''+4xy'+2y=2x^4+4x^2
\end{equation}

on \((-\infty,\infty)\).

Answer

The right side \(F(x)=2x^4+4x^2\) in \eqref{eq:2.3.17} is the sum of the right sides

\begin{eqnarray*}
F_1(x)=2x^4 \quad \mbox{ and } \quad F_2(x)=4x^2.
\end{eqnarray*}

in \eqref{eq:2.3.15} and \eqref{eq:2.3.16}. Therefore the principle of superposition implies that

\begin{eqnarray*}
y_p=y_{p_1}+y_{p_2}={x^4\over15}+{x^2\over3}
\end{eqnarray*}

is a particular solution of \eqref{eq:2.3.17}.