1.2E: Exercises

Exercise \(\PageIndex{1}\)

1. If \(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) and \(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), find the power series of \(\displaystyle \frac{1}{2}(f(x)+g(x))\) and of \(\displaystyle \frac{1}{2}(f(x)−g(x))\).

Answer

\(\displaystyle \frac{1}{2}(f(x)+g(x))=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) and \(\displaystyle \frac{1}{2}(f(x)−g(x))=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\).

2. If \(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) and \(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), find the power series of \(\displaystyle C(x)+S(x)\) and of \(\displaystyle C(x)−S(x)\).

Exercise \(\PageIndex{2}\)

In the following exercises, use partial fractions to find the power series of each function.

1. \(\displaystyle \frac{4}{(x−3)(x+1)}\)

Answer

\(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞(\frac{x}{3})^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞((−1)^{n+1}−\frac{1}{3n+1})x^n\)

2. \(\displaystyle \frac{3}{(x+2)(x−1)}\)

3. \(\displaystyle \frac{5}{(x^2+4)(x^2−1)}\)

Answer

\(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+(\frac{x}{2})^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n(\frac{x}{2})^n=\sum_{n=0}^∞((−1)+(−1)^{n+1}\frac{1}{2^{n+2}})x^{2n}\)

4. \(\displaystyle \frac{30}{(x^2+1)(x^2−9)}\)

Exercise \(\PageIndex{3}\)

In the following exercises, express each series as a rational function.

1. \(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

Answer

\(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

2. \(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

3. \(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

Answer

\(\displaystyle \frac{1}{x−3}\frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

4. \(\displaystyle \sum_{n=1}^∞(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}})\)

Exercise \(\PageIndex{4}\)

The following exercises explore applications of annuities.

1. Calculate the present values P of an annuity in which $10,000 is to be paid out annually for a period of 20 years, assuming interest rates of \(\displaystyle r=0.03,r=0.05\), and \(\displaystyle r=0.07\).

Answer

\(\displaystyle P=P_1+⋯+P_{20}\) where \(\displaystyle P_k=10,000\frac{1}{(1+r)^k}\). Then \(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). When \(\displaystyle r=0.03,P≈10,000×14.8775=148,775.\) When \(\displaystyle r=0.05,P≈10,000×12.4622=124,622.\) When \(\displaystyle r=0.07,P≈105,940\).

2. Calculate the present values P of annuities in which $9,000 is to be paid out annually perpetually, assuming interest rates of \(\displaystyle r=0.03,r=0.05\) and \(\displaystyle r=0.07\).

3. Calculate the annual payouts C to be given for 20 years on annuities having present value $100,000 assuming respective interest rates of \(\displaystyle r=0.03,r=0.05,\) and \(\displaystyle r=0.07.\)

Answer

In general, \(\displaystyle P=\frac{C(1−(1+r)^{−N})}{r}\) for N years of payouts, or \(\displaystyle C=\frac{Pr}{1−(1+r)^{−N}}\). For \(\displaystyle N=20\) and \(\displaystyle P=100,000\), one has \(\displaystyle C=6721.57\) when \(\displaystyle r=0.03;C=8024.26\) when \(\displaystyle r=0.05\); and \(\displaystyle C≈9439.29\) when \(\displaystyle r=0.07\).

4. Calculate the annual payouts C to be given perpetually on annuities having present value $100,000 assuming respective interest rates of \(\displaystyle r=0.03,r=0.05,\) and \(\displaystyle r=0.07\).

5. Suppose that an annuity has a present value \(\displaystyle P=1\) million dollars. What interest rate r would allow for perpetual annual payouts of $50,000?

Answer

In general, \(\displaystyle P=\frac{C}{r}.\) Thus, \(\displaystyle r=\frac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

6. Suppose that an annuity has a present value \(\displaystyle P=10\) million dollars. What interest rate r would allow for perpetual annual payouts of $100,000?

Exercise \(\PageIndex{5}\)

In the following exercises, express the sum of each power series in terms of geometric series, and then express the sum as a rational function.

1. \(\displaystyle x+x^2−x^3+x^4+x^5−x^6+⋯\) (Hint: Group powers \(\displaystyle x^{3k}, x^{3k−1},\) and \(\displaystyle x^{3k−2}\).)

Answer

\(\displaystyle (x+x^2−x^3)(1+x^3+x^6+⋯)=\frac{x+x^2−x^3}{1−x^3}\)

2. \(\displaystyle x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (Hint: Group powers \(\displaystyle x^{4k}, x^{4k−1},\) etc.)

3. \(\displaystyle x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (Hint: Group powers \(\displaystyle x^{3k}, x^{3k−1}\), and \(\displaystyle x^{3k−2}\).)

Answer

\(\displaystyle (x−x^2−x^3)(1+x^3+x^6+⋯)=\frac{x−x^2−x^3}{1−x^3}\)

4. \(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (Hint: Group powers \(\displaystyle \frac{x}{2})^{3k},(\frac{x}{2})^{3k−1},\) and \(\displaystyle \frac{x}{2})^{3k−2}\).

Exercise \(\PageIndex{6}\)

In the following exercises, find the power series of \(\displaystyle f(x)g(x)\) given f and g as defined.

1. \(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

Answer

\(\displaystyle a_n=2,b_n=n\) so \(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) and \(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

2. \(\displaystyle f(x)=\sum_{n=1}^∞x^n,g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Express the coefficients of \(\displaystyle f(x)g(x)\) in terms of \(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

3. \(\displaystyle f(x)=g(x)=\sum_{n=1}^∞(\frac{x}{2})^n\)

Answer

\(\displaystyle a_n=b_n=2^{−n}\) so \(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) and \(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(\frac{x}{2})^n\)

4. \(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

Exercise \(\PageIndex{7}\)

In the following exercises, differentiate the given series expansion of f term-by-term to obtain the corresponding series expansion for the derivative of f.

1. \(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

Answer

The derivative of \(\displaystyle f\) is \(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

2. \(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

In the following exercises, integrate the given series expansion of \(\displaystyle f\) term-by-term from zero to x to obtain the corresponding series expansion for the indefinite integral of \(\displaystyle f\).

3. \(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

Answer

The indefinite integral of \(\displaystyle f\) is \(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

4. \(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

Exercise \(\PageIndex{8}\)

In the following exercises, evaluate each infinite series by identifying it as the value of a derivative or integral of geometric series.

1. Evaluate \(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) as \(\displaystyle f′(\frac{1}{2})\) where \(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Answer

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x};f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}∣_{x=1/2}=\frac{1}{(1−x)^2}∣_{x=1/2}=4\) so \(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

2. Evaluate \(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) as \(\displaystyle f′(\frac{1}{3})\) where \(\displaystyle f(x)=\sum_{n=0}^∞x6n\).

3. Evaluate \(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) as \(\displaystyle f''(\frac{1}{2})\) where \(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

Answer

\(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x};f''(\frac{1}{2})=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}∣_{x=1/2}=\frac{2}{(1−x)^3}∣_{x=1/2}=16\) so \(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

4. Evaluate \(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) as \(\displaystyle ∫^1_0f(t)dt\) where \(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

Exercise \(\PageIndex{9}\)

In the following exercises, given that \(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), use term-by-term differentiation or integration to find power series for each function centered at the given point.

1. \(\displaystyle f(x)=lnx\) centered at \(\displaystyle x=1\) (Hint: \(\displaystyle x=1−(1−x)\))

Answer

\(\displaystyle ∫\sum(1−x)^ndx=∫\sum(−1)^n(x−1)^ndx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

2. \(\displaystyle ln(1−x)\) at \(\displaystyle x=0\)

3. \(\displaystyle ln(1−x^2)\) at \(\displaystyle x=0\)

Answer

\(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

4. \(\displaystyle f(x)=\frac{2x}{(1−x^2)^2}\) at \(\displaystyle x=0\)

5. \(\displaystyle f(x)=tan^{−1}(x^2)\) at \(\displaystyle x=0\)

Answer

\(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

6. \(\displaystyle f(x)=ln(1+x^2)\) at \(\displaystyle x=0\)

7. \(\displaystyle f(x)=∫^x_0lntdt\) where \(\displaystyle ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

Answer

Term-by-term integration gives \(\displaystyle ∫^x_0lntdt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}(\frac{1}{n}−\frac{1}{n+1})(x−1)^{n+1}=(x−1)lnx+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=xlnx−x.\)

Exercise \(\PageIndex{10}\)

In the following exercises, using a substitution if indicated, express each series in terms of elementary functions and find the radius of convergence of the sum.

1. \(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

2. \(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

Answer

\(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−ln(1−x)\) so \(\displaystyle \sum_{k=1}6∞\frac{x^{3k}}{6k}=−\frac{1}{6}ln(1−x^3)\). The radius of convergence is equal to 1 by the ratio test.

3. \(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) using \(\displaystyle y=\frac{1}{1+x^2}\)

4. \(\displaystyle \sum_{k=1}^∞2^{−kx}\) using \(\displaystyle y=2^{−x}\)

Answer

If \(\displaystyle y=2^{−x}\), then \(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). If \(\displaystyle a_k=2^{−kx}\), then \(\displaystyle \frac{a_{k+1}}{a_k}=2^{−x}<1\) when \(\displaystyle x>0\). So the series converges for all \(\displaystyle x>0\).

Exercise \(\PageIndex{11}\)

1. Show that, up to powers \(\displaystyle x^3\) and \(\displaystyle y^3\), \(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) satisfies \(\displaystyle E(x+y)=E(x)E(y)\).

2. Differentiate the series \(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) term-by-term to show that \(\displaystyle E(x)\) is equal to its derivative.

3. Show that if \(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) is a sum of even powers, that is, \(\displaystyle a_n=0\) if \(\displaystyle n\) is odd, then \(\displaystyle F=∫^x_0f(t)dt\) is a sum of odd powers, while if I is a sum of odd powers, then F is a sum of even powers.

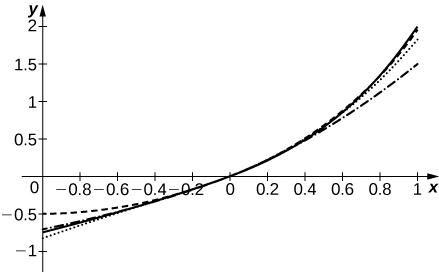
4. Suppose that the coefficients an of the series \(\displaystyle \sum_{n=0}^∞a_nx^n\) are defined by the recurrence relation \(\displaystyle a_n=\frac{a_{n−1}}{n}+\frac{a_{n−2}}{n(n−1)}\). For \(\displaystyle a_0=0\) and \(\displaystyle a_1=1\), compute and plot the sums \(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) for \(\displaystyle N=2,3,4,5\) on \(\displaystyle [−1,1].\)

Answer

The solid curve is \(\displaystyle S_5\). The dashed curve is \(\displaystyle S_2\), dotted is \(\displaystyle S_3\), and dash-dotted is \(\displaystyle S_4\)

5. Suppose that the coefficients an of the series \(\displaystyle \sum_{n=0}^∞a_nx^n\) are defined by the recurrence relation \(\displaystyle a_n=\frac{a_{n−1}}{\sqrt{n}}−\frac{a_{n−2}}{\sqrt{n(n−1)}}\). For \(\displaystyle a_0=1\) and \(\displaystyle a_1=0\), compute and plot the sums \(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) for \(\displaystyle N=2,3,4,5\) on \(\displaystyle [−1,1]\).

6. Given the power series expansion \(\displaystyle ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), determine how many terms N of the sum evaluated at \(\displaystyle x=−1/2\) are needed to approximate \(\displaystyle ln(2)\) accurate to within 1/1000. Evaluate the corresponding partial sum \(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).

Answer

When \(\displaystyle x=−\frac{1}{2},−ln(2)=ln(\frac{1}{2})=−\sum_{n=1}^∞\frac{1}{n2^n}\). Since \(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\) one has \(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\) whereas \(\displaystyle ln(2)=0.69314…;\) therefore, \(\displaystyle N=10.\)

7. Given the power series expansion \(\displaystyle tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), use the alternating series test to determine how many terms N of the sum evaluated at \(\displaystyle x=1\) are needed to approximate \(\displaystyle tan^{−1}(1)=\frac{π}{4}\) accurate to within 1/1000. Evaluate the corresponding partial sum \(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

8. Recall that \(\displaystyle tan^{−1}(\frac{1}{\sqrt{3}})=\frac{π}{6}.\) Assuming an exact value of \(\displaystyle \frac{1}{\sqrt{3}})\), estimate \(\displaystyle \frac{π}{6}\) by evaluating partial sums \(\displaystyle S_N(\frac{1}{\sqrt{3}})\) of the power series expansion \(\displaystyle tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) at \(\displaystyle x=\frac{1}{\sqrt{3}}\). What is the smallest number \(\displaystyle N\) such that \(\displaystyle 6S_N(\frac{1}{\sqrt{3}})\) approximates \(\displaystyle π\) accurately to within 0.001? How many terms are needed for accuracy to within 0.00001?

Answer

\(\displaystyle 6S_N(\frac{1}{\sqrt{3}})=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\) One has \(\displaystyle π−6S_4(\frac{1}{\sqrt{3}})=0.00101…\) and \(\displaystyle π−6S_5(\frac{1}{\sqrt{3}})=0.00028…\) so \(\displaystyle N=5\) is the smallest partial sum with accuracy to within 0.001. Also, \(\displaystyle π−6S_7(\frac{1}{\sqrt{3}})=0.00002…\) while \(\displaystyle π−6S_8(\frac{1}{\sqrt{3}})=−0.000007…\) so \(\displaystyle N=8\) is the smallest N to give accuracy to within 0.00001.