4.5: Constant Coefficient Homogeneous Systems II

Last updated
Save as PDF

Page ID: 17438

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Constant Coefficient Homogeneous Systems II

We saw in Section 4.4 that if an $n\times n$ constant matrix $A$ has $n$ real eigenvalues $\lambda_1$, $\lambda_2$, $\dots$, $\lambda_n$ (which need not be distinct) with associated linearly independent eigenvectors ${\bf x}_1$, ${\bf x}_2$, $\dots$, ${\bf x}_n$, then the general solution of ${\bf y}'=A{\bf y}$ is

\begin{eqnarray*}
{\bf y} = c_1{\bf x}_1 e^{\lambda_1 t} = c_2{\bf x}_2 e^{\lambda_2 t} + \cdots + c_n{\bf x}_n e^{\lambda_n t}.
\end{eqnarray*}

In this section we consider the case where $A$ has $n$ real eigenvalues, but does not have $n$ linearly independent eigenvectors. It is shown in linear algebra that this occurs if and only if $A$ has at least one eigenvalue of multiplicity $r>1$ such that the associated eigenspace has dimension less than $r$. In this case $A$ is said to be $ \textcolor{blue}{\mbox{defective}} $. Since it's beyond the scope of this book to give a complete analysis of systems with defective coefficient matrices, we will restrict our attention to some commonly occurring special cases.

Example$\PageIndex{1}$

Show that the system

\begin{equation}\label{eq:4.5.1}
{\bf y}'= \left[ \begin{array} \\ {11} & {-25} \\ 4 & {-9} \end{array} \right] {\bf y}
\end{equation}

does not have a fundamental set of solutions of the form $\{{\bf x}_1e^{\lambda_1t},{\bf x}_2e^{\lambda_2t}\}$, where $\lambda_1$ and $\lambda_2$ are eigenvalues of the coefficient matrix $A$ of \eqref{eq:4.5.1} and ${\bf x}_1$, and ${\bf x}_2$ are associated linearly independent eigenvectors.

Answer

The characteristic polynomial of $A$ is

\begin{eqnarray*}
\left[ \begin{array} \\ {11} -\lambda & {-25} \\ 4 & {-9} -\lambda \end{array} \right]
&=&(\lambda-11)(\lambda+9)+100\\
&=&\lambda^2-2\lambda+1=(\lambda-1)^2.
\end{eqnarray*}

Hence, $\lambda=1$ is the only eigenvalue of $A$. The augmented matrix of the system $(A-I){\bf x}={\bf 0}$ is

\begin{eqnarray*}
\left[ \begin{array} \\ 10 & -25 & \vdots & 0 \\ 4 & -10 & \vdots $ 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & -\displaystyle{5 \over 2} & \vdots & 0 \\ 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $x_1=5x_2/2$ where $x_2$ is arbitrary. Therefore all eigenvectors of $A$ are scalar multiples of ${\bf x}_1 = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right]$, so $A$ does not have a set of two linearly independent eigenvectors.

From Example $(4.5.1)$, we know that all scalar multiples of ${\bf y}_1 = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] e^t$ are solutions of \eqref{eq:4.5.1}; however, to find the general solution we must find a second solution ${\bf y}_2$ such that $\{{\bf y}_1,{\bf y}_2\}$ is linearly independent. Based on your recollection of the procedure for solving a constant coefficient scalar equation

\begin{eqnarray*}
ay'' + by' + cy = 0
\end{eqnarray*}

in the case where the characteristic polynomial has a repeated root, you might expect to obtain a second solution of \eqref{eq:4.5.1} by multiplying the first solution by $t$. However, this yields ${\bf y}_2 = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] te^t$, which doesn't work, since

\begin{eqnarray*}
{\bf y}_2' = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] (t e^t + e^t), \quad \mbox{while} \quad \left[ \begin{array} \\ 11 & -25 \\ 4 & -9 \end{array} \right] {\bf y}_2 = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] t e^t.
\end{eqnarray*}

The next theorem shows what to do in this situation.

Theorem $\PageIndex{1}$

Suppose the $n\times n$ matrix $A$ has an eigenvalue $\lambda_1$ of multiplicity $\ge2$ and the associated eigenspace has dimension $1;$ that is, all $\lambda_1$-eigenvectors of $A$ are scalar multiples of an eigenvector ${\bf x}$. Then there are infinitely many vectors ${\bf u}$ such that

\begin{equation}\label{eq:4.5.2}
(A-\lambda_1I){\bf u}={\bf x}.
\end{equation}

Moreover, if ${\bf u}$ is any such vector then

\begin{equation}\label{eq:4.5.3}
{\bf y}_1={\bf x}e^{\lambda_1t} \quad \mbox{and } \quad {\bf y}_2={\bf u}e^{\lambda_1t}+{\bf x}te^{\lambda_1t}
\end{equation}

are linearly independent solutions of ${\bf y}'=A{\bf y}$.

Proof: Add proof here and it will automatically be hidden if you have a "AutoNum" template active on the page.

A complete proof of this theorem is beyond the scope of this book. The difficulty is in proving that there's a vector ${\bf u}$ satisfying \eqref{eq:4.5.2}, since $\det(A-\lambda_1I)=0$. We'll take this without proof and verify the other assertions of the theorem.

We already know that ${\bf y}_1$ in \eqref{eq:4.5.3} is a solution of ${\bf y}'=A{\bf y}$. To see that ${\bf y}_2$ is also a solution, we compute

\begin{eqnarray*}
{\bf y}_2'-A{\bf y}_2&=&\lambda_1{\bf u}e^{\lambda_1t}+{\bf x} e^{\lambda_1t}
+\lambda_1{\bf x} te^{\lambda_1t}-A{\bf u}e^{\lambda_1t}-A{\bf x} te^{\lambda_1t}\\
&=&(\lambda_1{\bf u}+{\bf x} -A{\bf u})e^{\lambda_1t}+(\lambda_1{\bf x} -A{\bf x} )te^{\lambda_1t}.
\end{eqnarray*}

Since $A{\bf x}=\lambda_1{\bf x}$, this can be written as

\begin{eqnarray*}
{\bf y}_2' - A{\bf y}_2 = - \left( (A -\lambda_1 l) {\bf u} - {\bf x} \right) e^{\lambda_1 t},
\end{eqnarray*}

and now \eqref{eq:4.5.2} implies that ${\bf y}_2'=A{\bf y}_2$.

To see that ${\bf y}_1$ and ${\bf y}_2$ are linearly independent, suppose $c_1$ and $c_2$ are constants such that

\begin{equation}\label{eq:4.5.4}
c_1{\bf y}_1+c_2{\bf y}_2=c_1{\bf x}e^{\lambda_1t}+c_2({\bf u}e^{\lambda_1t} +{\bf x}te^{\lambda_1t})={\bf 0}.
\end{equation}

We must show that $c_1=c_2=0$. Multiplying \eqref{eq:4.5.4} by $e^{-\lambda_1t}$ shows that

\begin{equation}\label{eq:4.5.5}
c_1{\bf x}+c_2({\bf u} +{\bf x}t)={\bf 0}.
\end{equation}

By differentiating this with respect to $t$, we see that $c_2{\bf x}={\bf 0}$, which implies $c_2=0$, because ${\bf x}\ne{\bf 0}$. Substituting $c_2=0$ into \eqref{eq:4.5.5} yields $c_1{\bf x}={\bf 0}$, which implies that $c_1=0$, again because ${\bf x}\ne{\bf 0}$

Example $\PageIndex{2}$

Use Theorem $(4.5.1)$ to find the general solution of the system

\begin{equation}\label{eq:4.5.6}
{\bf y}' = \left[ \begin{array} \\ {11} & {-25} \\ 4 & {-9} \end{array} \right] {\bf y}
\end{equation}

considered in Example $(4.5.1)$.

Answer

In Example $(4.5.1)$ we saw that $\lambda_1=1$ is an eigenvalue of multiplicity $2$ of the coefficient matrix $A$ in \eqref{eq:4.5.6}, and that all of the eigenvectors of $A$ are multiples of

\begin{eqnarray*}
{\bf x} = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right].
\end{eqnarray*}

Therefore

\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] e^t
\end{eqnarray*}

is a solution of \eqref{eq:4.5.6}. From Theorem $(4.5.1)$, a second solution is given by ${\bf y}_2={\bf u}e^t+{\bf x}te^t$, where $(A-I){\bf u}={\bf x}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ 10 & -25 & \vdots & 5 \\ 4 & -10 & \vdots & 2 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & -{5 \over 2} & \vdots & {1 \over 2} \\ 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Therefore the components of ${\bf u}$ must satisfy

\begin{eqnarray*}
u_1 - {5 \over 2} u_2 = {1 \over 2},
\end{eqnarray*}

where $u_2$ is arbitrary. We choose $u_2=0$, so that $u_1=1/2$ and

\begin{eqnarray*}
{\bf u} = \left[ \begin{array} \\ {1 \over 2} \\ 0 \end{array} \right].
\end{eqnarray*}

Thus,

\begin{eqnarray*}
{\bf y}_2 = \left[ \begin{array} \\ 1 \\ 0 \end{array} \right] {e^t \over 2} + \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] e^t.
\end{eqnarray*}

Since ${\bf y}_1$ and ${\bf y}_2$ are linearly independent by Theorem $(4.5.1)$, they form a fundamental set of solutions of \eqref{eq:4.5.6}. Therefore the general solution of \eqref{eq:4.5.6} is

\begin{eqnarray*}
{\bf y} = c_1 \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] e^t + c_2 \left( \left[ \begin{array} \\ 1 \\ 0 \end{array} \right] {e^t \over 2} + \left[ \begin{array} \\ 5 \\ 2 \end{array} \right] t e^t \right)
\end{eqnarray*}

Note that choosing the arbitrary constant $u_2$ to be nonzero is equivalent to adding a scalar multiple of ${\bf y}_1$ to the second solution ${\bf y}_2$ (Exercise $(4.5E.33)$).

Example $\PageIndex{3}$

Find the general solution of

\begin{equation}\label{eq:4.5.7}
{\bf y}' = \left[ \begin{array} \\ 3 & 4 & {-10} \\ 2 & 1 & {-2} \\ 2 & 2 & {-5} \end{array} \right] {\bf y}.
\end{equation}

Answer

The characteristic polynomial of the coefficient matrix $A$ in \eqref{eq:4.5.7} is

\begin{eqnarray*}
\left[ \begin{array} \\ 3-\lambda & 4 & -10 \\ 2 & 1-\lambda & -2 \\ 2 & 2 & -5-\lambda \end{array} \right] = -(\lambda-1)(\lambda+1)^2.
\end{eqnarray*}

Hence, the eigenvalues are $\lambda_1=1$ with multiplicity $1$ and $\lambda_2=-1$ with multiplicity $2$.

Eigenvectors associated with $\lambda_1=1$ must satisfy $(A-I){\bf x}={\bf 0}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ 2 & 4 & -10 & \vdots & 0 \\ 2 & 0 & -2 & \vdots & 0 \\ 2 & 2 & -6 & \vdots & 0 \end{array} \right]
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -1 & \vdots & 0 \\ 0 & 1 & -2 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $x_1 =x_3$ and $x_2 =2 x_3$, where $x_3$ is arbitrary. Choosing $x_3=1$ yields the eigenvector

\begin{eqnarray*}
{\bf x}_1 = \left[ \begin{array} \\ 1 \\ 2 \\ 1 \end{array} \right].
\end{eqnarray*}

Therefore

\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ 1 \\ 2 \\ 1 \end{array} \right] e^t
\end{eqnarray*}

is a solution of \eqref{eq:4.5.7}.

Eigenvectors associated with $\lambda_2 =-1$ satisfy $(A+I){\bf x}={\bf 0}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ 4 & 4 & -10 & \vdots & 0 \\ 2 & 2 & -2 & \vdots & 0 \\ 2 & 2 & -4 & \vdots & 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 1 & 0 & \vdots & 0 \\ 0 & 0 & 1 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $x_3=0$ and $x_1 =-x_2$, where $x_2$ is arbitrary. Choosing $x_2=1$ yields the eigenvector

\begin{eqnarray*}
{\bf y}_2 = \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right],
\end{eqnarray*}

\begin{eqnarray*}
{\bf y}_2 = \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] e^{-t}
\end{eqnarray*}

is a solution of \eqref{eq:4.5.7}.

Since all the eigenvectors of $A$ associated with $\lambda_2=-1$ are multiples of ${\bf x}_2$, we must now use Theorem $(4.5.1)$ to find a third solution of \eqref{eq:4.5.7} in the form

\begin{equation}\label{eq:4.5.8}
{\bf y}_3={\bf u}e^{-t} + \left[ \begin{array} \\ {-1} \\ 1 \\ 0 \end{array} \right] te^{-t},
\end{equation}

where ${\bf u}$ is a solution of $(A+I){\bf u=x}_2$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ 4 & 4 & -10 & \vdots & -1 \\ 2 & 2 & -2 & \vdots & 1 \\ 2 & 2 & -4 & \vdots & 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 1 & 0 & \vdots & 0 \\ 0 & 0 & 1 & \vdots & {1 \over 2} \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $u_3=1/2$ and $u_1 =1-u_2$, where $u_2$ is arbitrary. Choosing $u_2=0$ yields

\begin{eqnarray*}
{\bf u} = \left[ \begin{array} \\ 1 \\ 0 \\ {1 \over 2} \end{array} \right],
\end{eqnarray*}

and substituting this into \eqref{eq:4.5.8} yields the solution

\begin{eqnarray*}
{\bf y}_3 = \left[ \begin{array} \\ 2 \\ 0 \\ 1 \end{array} \right] {e^{-t} \over 2} + \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] t e^{-t}
\end{eqnarray*}

of \eqref{eq:4.5.7}.

Since the Wronskian of $\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}$ at $t=0$ is

\begin{eqnarray*}
\left| \begin{array} \\ 1 & -1 & 1 \\ 2 & 1 & 0 \\ 1 & 0 & {1 \over 2} \end{array} \right| = {1 \over 2},
\end{eqnarray*}

$\{{\bf y}_1,{\bf y}_2,{\bf y}_3\}$ is a fundamental set of solutions of \eqref{eq:4.5.7}. Therefore the general solution of \eqref{eq:4.5.7} is

\begin{eqnarray*}
{\bf y} = c_1 \left[ \begin{array} \\ 1 \\ 2 \\ 1 \end{array} \right] e^t + c_2 \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] e^{-t} + c_3 \left( \left[ \begin{array} \\ 2 \\ 0 \\ 1 \end{array} \right] {e^{-t} \over 2} + \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] e^{-t} \right).
\end{eqnarray*}

Theorem $\PageIndex{2}$

Suppose the $n\times n$ matrix $A$ has an eigenvalue $\lambda_1$ of multiplicity $\ge 3$ and the associated eigenspace is one-dimensional; that is, all eigenvectors associated with $\lambda_1$ are scalar multiples of the eigenvector ${\bf x}.$ Then there are infinitely many vectors ${\bf u}$ such that

\begin{equation}\label{eq:4.5.9}
(A-\lambda_1I){\bf u}={\bf x},
\end{equation}

and, if ${\bf u}$ is any such vector, there are infinitely many vectors ${\bf v}$ such that

\begin{equation}\label{eq:4.5.10}
(A-\lambda_1I){\bf v}={\bf u}.
\end{equation}

If ${\bf u}$ satisfies {\rm\eqref{eq:4.5.9}} and ${\bf v}$ satisfies \eqref{eq:4.5.10}, then

\begin{eqnarray*}
{\bf y}_1 &=&{\bf x} e^{\lambda_1t},\\
{\bf y}_2&=&{\bf u}e^{\lambda_1t}+{\bf x} te^{\lambda_1t},\mbox{
and }\\
{\bf y}_3&=&{\bf v}e^{\lambda_1t}+{\bf u}te^{\lambda_1t}+{\bf
x} {t^2e^{\lambda_1t}\over2}
\end{eqnarray*}

are linearly independent solutions of ${\bf y}'=A{\bf y}$.

Proof: Add proof here and it will automatically be hidden if you have a "AutoNum" template active on the page.

Again, it's beyond the scope of this book to prove that there are vectors ${\bf u}$ and ${\bf v}$ that satisfy \eqref{eq:4.5.9} and
\eqref{eq:4.5.10}. Theorem $(4.5.1)$ implies that ${\bf y}_1$ and ${\bf y}_2$ are solutions of ${\bf y}'=A{\bf y}$. We leave the rest of the proof to you (Exercise $(4.5E.34)$).

Example $\PageIndex{4}$

Use Theorem $(4.5.2)$ to find the general solution of

\begin{equation}\label{eq:4.5.11}
{\bf y}' = \left[ \begin{array} \\ 1 & 1 & 1 \\ 1 & 3 & {-1} \\ 0 & 2 & 2 \end{array} \right] {\bf y}.
\end{equation}

Answer

The characteristic polynomial of the coefficient matrix $A$ in \eqref{eq:4.5.11} is

\begin{eqnarray*}
\left| \begin{array} \\ 1-\lambda & 1 & \phantom{-}1 \\ 1 & 3-\lambda & -1 \\ 0 & 2 & -\lambda \end{array} \right| = -(\lambda-2)^3.
\end{eqnarray*}

Hence, $\lambda_1=2$ is an eigenvalue of multiplicity $3$. The associated eigenvectors satisfy $(A-2I){\bf x=0}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ -1 & 1 & 1 & \vdots & 0 \\ 1 & 1 & -1 & \vdots & 0 \\ 0 & 2 & 0 & \vdots & 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -1 & \vdots & 0 \\ 0 & 1 & 0 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $x_1 =x_3$ and $x_2 = 0$, so the eigenvectors are all scalar multiples of

\begin{eqnarray*}
{\bf x}_1 = \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right].
\end{eqnarray*}

Therefore

\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] e^{2t}
\end{eqnarray*}

is a solution of \eqref{eq:4.5.11}.

We now find a second solution of \eqref{eq:4.5.11} in the form

\begin{eqnarray*}
{\bf y}_2 = {\bf u} e^{2t} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] t e^{2t},
\end{eqnarray*}

where ${\bf u}$ satisfies $(A-2I){\bf u=x}_1$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ -1 & 1 & 1 & \vdots & 1 \\ 1 & 1 & -1 & \vdots & 0 \\ 0 & 2 & 0 & \vdots & 1 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -1 & \vdots & -{1 \over 2} \\ 0 & 1 & 0 & \vdots & {1 \over 2} \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Letting $u_3=0$ yields $u_1=-1/2$ and $u_2=1/2$; hence,

\begin{eqnarray*}
{\bf u} = {1 \over 2} \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right]
\end{eqnarray*}

and

\begin{eqnarray*}
{\bf y}_2 = \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] {e^{2t} \over 2} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] t e^{2t}
\end{eqnarray*}

is a solution of \eqref{eq:4.5.11}.

We now find a third solution of \eqref{eq:4.5.11} in the form

\begin{eqnarray*}
{\bf y}_3 = {\bf v} e^{2t} + \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] {t e^{2t} \over 2} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] {t^2 e^{2t} \over 2}
\end{eqnarray*}

where ${\bf v}$ satisfies $(A-2I){\bf v}={\bf u}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ -1 & 1 & 1 & \vdots & -{1 \over 2} \\ 1 & 1 & -1 & \vdots & {1 \over 2} \\ 0 & 2 & 0 & \vdots & 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array}\\ 1 & 0 & -1 & \vdots & {1 \over 2} \\ 0 & 1 & 0 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Letting $v_3=0$ yields $v_1=1/2$ and $v_2=0$; hence,

\begin{eqnarray*}
{\bf v} = {1 \over 2} \left[ \begin{array} \\ 1 \\ 0 \\ 0 \end{array} \right].
\end{eqnarray*}

Therefore

\begin{eqnarray*}
{\bf y}_3 = \left[ \begin{array} \\ 1 \\ 0 \\ 0 \end{array} \right] {e^{2t} \over 2} + \left[ \begin{array} \\ -1 \\ 1 \\ 0 \end{array} \right] {t e^{2t} \over 2} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] {t^2 e^{2t} \over 2}
\end{eqnarray*}

is a solution of \eqref{eq:4.5.11}. Since ${\bf y}_1$, ${\bf y}_2$, and ${\bf y}_3$ are linearly independent by Theorem $(4.5.2)$, they form a fundamental set of solutions of \eqref{eq:4.5.11}. Therefore the general solution of \eqref{eq:4.5.11} is

\begin{eqnarray*}
{\bf y} &=& c_1 \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] e^{2t} + c_2 \left( \left[ \begin{array} \\ {-1} \\ 1 \\ 0 \end{array} \right] {e^{2t}\over2} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] te^{2t} \right)\\
&& + c_3 \left( \left[ \begin{array} \\ 1 \\ 0 \\ 0 \end{array} \right] {e^{2t}\over2} + \left[ \begin{array} \\ {-1} \\ 1 \\ 0 \end{array} \right] {te^{2t}\over2} + \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] {t^2e^{2t}\over2} \right).
\end{eqnarray*}

Theorem $\PageIndex{3}$

Suppose the $n\times n$ matrix $A$ has an eigenvalue $\lambda_1$ of multiplicity $\ge 3$ and the associated eigenspace is two-dimensional; that is, all eigenvectors of $A$ associated with $\lambda_1$ are linear combinations of two linearly independent eigenvectors ${\bf x}_1$ and ${\bf x}_2$. Then there are constants $\alpha$ and $\beta$ (not both zero) such that if

\begin{equation}\label{eq:4.5.12}
{\bf x}_3=\alpha{\bf x}_1+\beta{\bf x}_2,
\end{equation}

then there are infinitely many vectors ${\bf u}$ such that

\begin{equation}\label{eq:4.5.13}
(A-\lambda_1I){\bf u}={\bf x}_3.
\end{equation}

If ${\bf u}$ satisfies \eqref{eq:4.5.13}, then

\begin{eqnarray}
{\bf y}_1&=&{\bf x}_1 e^{\lambda_1t},\nonumber\\
{\bf y}_2&=&{\bf x}_2e^{\lambda_1t},\mbox{and }\nonumber\\
{\bf y}_3&=&{\bf u}e^{\lambda_1t}+{\bf x}_3te^{\lambda_1t}\label{eq:4.5.14},
\end{eqnarray}

are linearly independent solutions of ${\bf y}'=A{\bf y}.$

Proof: We omit the proof of this theorem.

Example $\PageIndex{5}$

Use Theorem $(4.5.3)$ to find the general solution of

\begin{equation}\label{eq:4.5.15}
{\bf y}' = \left[ \begin{array} \\ 0 & 0 & 1 \\ {-1} & 1 & 1 \\ {-1} & 0 & 2 \end{array} \right] {\bf y}.
\end{equation}

Answer

The characteristic polynomial of the coefficient matrix $A$ in \eqref{eq:4.5.15} is

\begin{eqnarray*}
\left| \begin{array} \\ -\lambda & 0 & 1 \\ -1 & 1-\lambda & 1 \\ -1 & 0 & 2-\lambda \end{array} \right| = -(\lambda-1)^3.
\end{eqnarray*}

Hence, $\lambda_1=1$ is an eigenvalue of multiplicity $3$. The associated eigenvectors satisfy $(A-I){\bf x=0}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ -1 & 0 & 1 & \vdots & 0 \\ -1 & 0 & 1 & \vdots & 0 \\ -1 & 0 & 1 & \vdots & 0 \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -1 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

Hence, $x_1 =x_3$ and $x_2$ is arbitrary, so the eigenvectors are of the form

\begin{eqnarray*}
{\bf x}_1 = \left[ \begin{array} \\ x_3 \\ x_2 \\ x_3 \end{array} \right] = x_3 \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] + x_2 \left[ \begin{array} \\ 0 \\ 1 \\ 0 \end{array} \right].
\end{eqnarray*}

Therefore the vectors

\begin{equation}\label{eq:4.5.16}
{\bf x}_1 = \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] \quad \mbox{and} \quad {\bf x}_2 = \left[ \begin{array} \\ 0 \\ 1 \\ 0 \end{array} \right]
\end{equation}

form a basis for the eigenspace, and

\begin{eqnarray*}
{\bf y}_1 = \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] e^t \quad \mbox{and} \quad {\bf y}_2 = \left[ \begin{array} \\ 0 \\ 1 \\ 0 \end{array} \right] e^t
\end{eqnarray*}

are linearly independent solutions of \eqref{eq:4.5.15}.

To find a third linearly independent solution of \eqref{eq:4.5.15}, we must find constants $\alpha$ and $\beta$ (not both zero) such that the system

\begin{equation}\label{eq:4.5.17}
(A-I){\bf u}=\alpha{\bf x}_1+\beta{\bf x}_2
\end{equation}

has a solution ${\bf u}$. The augmented matrix of this system is

\begin{eqnarray*}
\left[ \begin{array} \\ -1 & 0 & 1 & \vdots & \alpha \\ -1 & 0 & 1 & \vdots & \beta \\ -1 & 0 & 1 & \vdots & \alpha \end{array} \right],
\end{eqnarray*}

which is row equivalent to

\begin{equation}\label{eq:4.5.18}
\left[\begin{array}{rrrcr} 1 & 0 &- 1 &\vdots& -\alpha\\ 0 & 0 & 0
&\vdots&\beta-\alpha\\ 0 & 0 & 0 &\vdots&0\end{array}
\right].
\end{equation}

Therefore \eqref{eq:4.5.17} has a solution if and only if $\beta=\alpha$, where $\alpha$ is arbitrary. If $\alpha=\beta=1$ then \eqref{eq:4.5.12} and \eqref{eq:4.5.16} yield

\begin{eqnarray*}
{\bf x}_3 = {\bf x}_1 + {\bf x}_2 = \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] + \left[ \begin{array} \\ 0 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array} \\ 1 \\ 1 \\ 1 \end{array} \right],
\end{eqnarray*}

and the augmented matrix \eqref{eq:4.5.18} becomes

\begin{eqnarray*}
\left[ \begin{array} \\ 1 & 0 & -1 & \vdots & -1 \\ 0 & 0 & 0 & \vdots & 0 \\ 0 & 0 & 0 & \vdots & 0 \end{array} \right].
\end{eqnarray*}

This implies that $u_1=-1+u_3$, while $u_2$ and $u_3$ are arbitrary. Choosing $u_2=u_3=0$ yields

\begin{eqnarray*}
{\bf u} = \left[ \begin{array} \\ -1 \\ 0 \\ 0 \end{array} \right].
\end{eqnarray*}

Therefore \eqref{eq:4.5.14} implies that

\begin{eqnarray*}
{\bf y}_3 = {\bf u} e^t + {\bf x}_3 t e^t = \left[ \begin{array} \\ -1 \\ 0 \\ 0 \end{array} \right] e^t + \left[ \begin{array} \\ 1 \\ 1 \\ 1 \end{array} \right] t e^t
\end{eqnarray*}

is a solution of \eqref{eq:4.5.15}. Since ${\bf y}_1$, ${\bf y}_2$, and ${\bf y}_3$ are linearly independent by Theorem $(4.5.3)$, they form a fundamental set of solutions for \eqref{eq:4.5.15}. Therefore the general solution of \eqref{eq:4.5.15} is

\begin{eqnarray*}
{\bf y} = c_1 \left[ \begin{array} \\ 1 \\ 0 \\ 1 \end{array} \right] e^t + c_2 \left[ \begin{array} \\ 0 \\ 1 \\ 0 \end{array} \right] e^t + c_3 \left( \left[ \begin{array} \\ -1 \\ 0 \\ 0 \end{array} \right] e^t + \left[ \begin{array} \\ 1 \\ 1 \\ 1 \end{array} \right] e^t \right)
\end{eqnarray*}

Geometric Properties of Solutions when $n=2$

We'll now consider the geometric properties of solutions of a $2\times2$ constant coefficient system

\begin{equation} \label{eq:4.5.19}
\left[ \begin{array} \\ {y_1'} \\ {y_2'} \end{array} \right] = \left[ \begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}
\end{array}\right] \left[ \begin{array} \\ {y_1} \\ {y_2} \end{array} \right]
\end{equation}

under the assumptions of this section; that is, when the matrix

\begin{eqnarray*}
A = \left[ \begin{array} \\ a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]
\end{eqnarray*}

has a repeated eigenvalue $\lambda_1$ and the associated eigenspace is one-dimensional. In this case we know from Theorem $(4.5.1)$ that the general solution of \eqref{eq:4.5.19} is

\begin{equation} \label{eq:4.5.20}
{\bf y}=c_1{\bf x}e^{\lambda_1t}+c_2({\bf u}e^{\lambda_1t}+{\bf
x}te^{\lambda_1t}),
\end{equation}

where ${\bf x}$ is an eigenvector of $A$ and ${\bf u}$ is any one of the infinitely many solutions of

\begin{equation} \label{eq:4.5.21}
(A-\lambda_1I){\bf u}={\bf x}.
\end{equation}

We assume that $\lambda_1\ne0$.

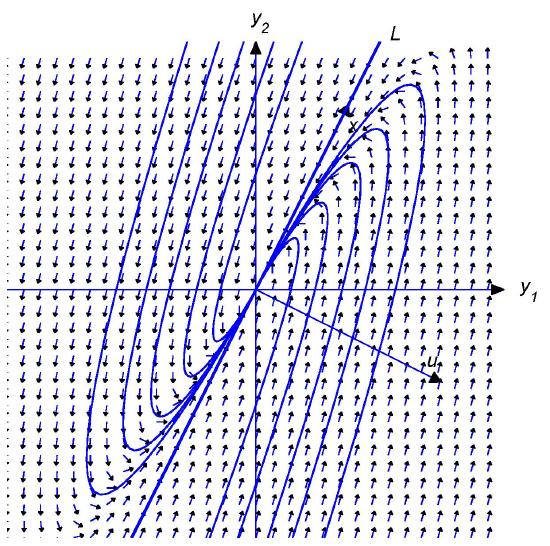
Figure $4.5.1$

Positive and negative half-planes

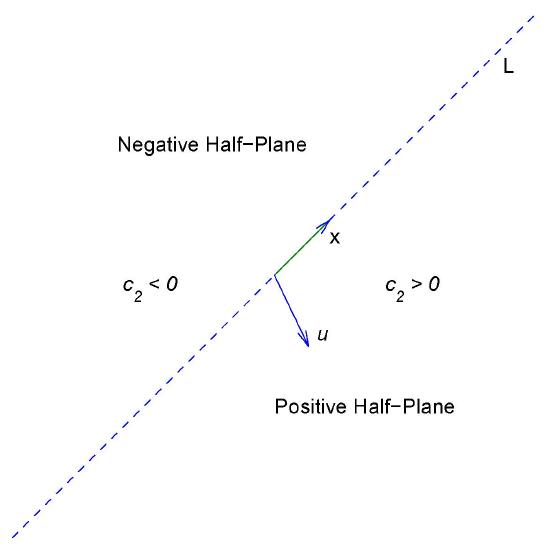
$fig100501.jpg$

Let $L$ denote the line through the origin parallel to ${\bf x}$. By a $ \textcolor{blue}{\mbox{half-line}} $ of $L$ we mean either of the rays obtained by removing the origin from $L$. Equation \eqref{eq:4.5.20} is a parametric equation of the half-line of $L$ in the direction of ${\bf x}$ if $c_1>0$, or of the half-line of |(L\) in the direction of $-{\bf x}$ if $c_1<0$. The origin is the trajectory of the trivial solution ${\bf y}\equiv{\bf 0}$.

Henceforth, we assume that $c_2\ne0$. In this case, the trajectory of \eqref{eq:4.5.20} can't intersect $L$, since every point of $L$ is on a trajectory obtained by setting $c_2=0$. Therefore the trajectory of \eqref{eq:4.5.20} must lie entirely in one of the open half-planes bounded by $L$, but does not contain any point on $L$. Since the initial point $(y_1(0),y_2(0))$ defined by ${\bf y}(0)=c_1{\bf x}_1+c_2{\bf u}$ is on the trajectory, we can determine which half-plane contains the trajectory from the sign of $c_2$, as shown in Figure $4.5.1$. For convenience we'll call the half-plane where $c_2>0$ the $ \textcolor{blue}{\mbox{positive half-plane}} $. Similarly, the-half plane where $c_2<0$ is the $ \textcolor{blue}{\mbox{negative half-plane}} $. You should convince yourself (Exercise $(4.5E.35)$) that even though there are infinitely many vectors ${\bf u}$ that satisfy \eqref{eq:4.5.21}, they all define the same positive and negative half-planes. In the figures simply regard ${\bf u}$ as an arrow pointing to the positive half-plane, since wen't attempted to give ${\bf u}$ its proper length or direction in comparison with ${\bf x}$. For our purposes here, only the relative orientation of ${\bf x}$ and ${\bf u}$ is important; that is, whether the positive half-plane is to the right of an observer facing the direction of ${\bf x}$ (as in Figures $4.5.2$ and $4.5.5$), or to the left of the observer (as in Figures $4.5.3$ and $4.5.4$).

Multiplying \eqref{eq:4.5.20} by $e^{-\lambda_1t}$ yields

\begin{eqnarray*}
e^{-\lambda_1 t} {\bf y}(t) = c_1{\bf x} + c_2{\bf u} + c_2 t {\bf x}.
\end{eqnarray*}

Since the last term on the right is dominant when $|t|$ is large, this provides the following information on the direction of ${\bf y}(t)$:

(a) Along trajectories in the positive half-plane ($c_2>0$), the direction of ${\bf y}(t)$ approaches the direction of ${\bf x}$ as $t\to\infty$ and the direction of $-{\bf x}$ as $t\to-\infty$.

(b) Along trajectories in the negative half-plane ($c_2<0$), the direction of ${\bf y}(t)$ approaches the direction of $-{\bf x}$ as $t\to\infty$ and the direction of ${\bf x}$ as $t\to-\infty$.

Since

\begin{eqnarray*}
\lim_{t\to\infty} \| {\bf y}(t) \| = \infty \quad \mbox{and} \quad \lim_{t\to-\infty}{\bf y}(t) = {\bf 0} \quad \mbox{if} \quad \lambda_1>0,
\end{eqnarray*}

\begin{eqnarray*}
\lim_{t-\to\infty} \| {\bf y}(t) \| = \infty \quad \mbox{and} \quad \lim_{t\to\infty}{\bf y}(t) = {\bf 0} \quad \mbox{if} \quad \lambda_1<0,
\end{eqnarray*}

there are four possible patterns for the trajectories of \eqref{eq:4.5.19}, depending upon the signs of $c_2$ and $\lambda_1$.
Figures $4.5.2$ to $4.5.5$ illustrate these patterns, and reveal the following principle:

If $\lambda_1$ and $c_2$ have the same sign then the direction of the trajectory approaches the direction of $-{\bf x}$ as $\|{\bf y} \|\to0$ and the direction of ${\bf x}$ as $\|{\bf y}\|\to\infty$ If $\lambda_1$ and $c_2$ have opposite signs then the direction of the trajectory approaches the direction of ${\bf x}$ as $\|{\bf y} \|\to0$ and the direction of $-{\bf x}$ as $\|{\bf y}\|\to\infty$.

Figure $4.5.2$

Positive eigenvalue; motion away from the origin

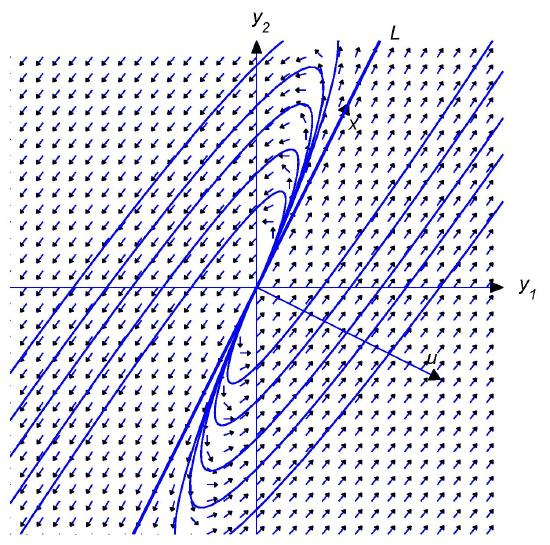
Positive eigenvalue; motion away from the origin

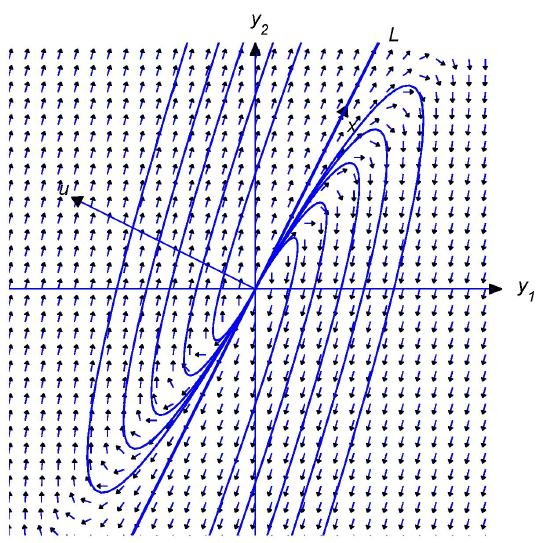
Negative eigenvalue; motion toward the origin

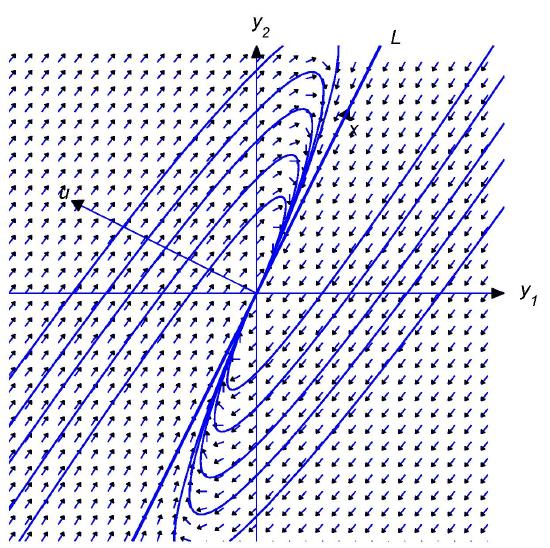
$fig100504.jpg$

Figure $4.5.5$

Negative eigenvalue; motion toward the origin

$fig100505.jpg$