7.3: Double Integrals in Polar Coordinates

Double integrals are sometimes much easier to evaluate if we change rectangular coordinates to polar coordinates. However, before we describe how to make this change, we need to establish the concept of a double integral in a polar rectangular region.

Polar Rectangular Regions of Integration

When we defined the double integral for a continuous function in rectangular coordinates—say, \(g\) over a region \(R\) in the \(xy\)-plane—we divided \(R\) into subrectangles with sides parallel to the coordinate axes. These sides have either constant \(x\)-values and/or constant \(y\)-values. In polar coordinates, the shape we work with is a polar rectangle, whose sides have constant \(r\)-values and/or constant \(\theta\)-values. This means we can describe a polar rectangle as in Figure \(\PageIndex{1a}\), with \(R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\).

Figure \(\PageIndex{1}\): (a) A polar rectangle \(R\) (b) divided into subrectangles \(R_{ij}\) (c) Close-up of a subrectangle.

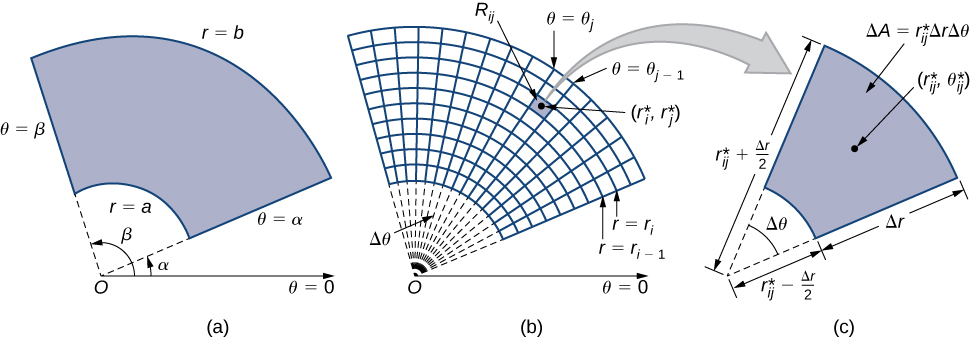
In this section, we are looking to integrate over polar rectangles. Consider a function \(f(r,\theta)\) over a polar rectangle \(R\). We divide the interval \([a,b]\) into \(m\) subintervals \([r_{i-1}, r_i]\) of length \(\Delta r = (b - a)/m\) and divide the interval \([\alpha, \beta]\) into \(n\) subintervals \([\theta_{i-1}, \theta_i]\) of width \(\Delta \theta = (\beta - \alpha)/n\). This means that the circles \(r = r_i\) and rays \(\theta = \theta_i\) for \(1 \leq i \leq m\) and \(1 \leq j \leq n\) divide the polar rectangle \(R\) into smaller polar subrectangles \(R_ij\) (Figure \(\PageIndex{1b}\)).

As before, we need to find the area \(\Delta A\) of the polar subrectangle \(R_{ij}\) and the “polar” volume of the thin box above \(R_{ij}\). Recall that, in a circle of radius \(r\) the length \(s\) of an arc subtended by a central angle of \(\theta\) radians is \(s = r\theta\). Notice that the polar rectangle \(R_{ij}\) looks a lot like a trapezoid with parallel sides \(r_{i-1}\Delta \theta\) and \(r_i\Delta \theta\) and with a width \(\Delta r\). Hence the area of the polar subrectangle \(R_{ij}\) is

\[\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_1 \delta \theta ).\]

Simplifying and letting \(r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i)\), we have \(\Delta A = r_{ij}^* \Delta r \Delta \theta\).

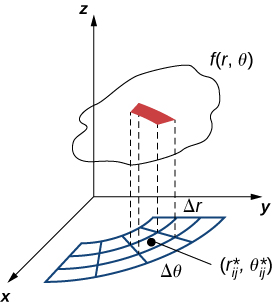
Therefore, the polar volume of the thin box above \(R_{ij}\) (Figure \(\PageIndex{2}\)) is

\[f(r_{ij}^*, \theta_{ij}^*) b\Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta.\]

Figure \(\PageIndex{2}\): Finding the volume of the thin box above polar rectangle \(R_{ij}\).

Using the same idea for all the subrectangles and summing the volumes of the rectangular boxes, we obtain a double Riemann sum as

\[\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta.\]

As we have seen before, we obtain a better approximation to the polar volume of the solid above the region \(R\) when we let \(m\) and \(n\) become larger. Hence, we define the polar volume as the limit of the double Riemann sum,

\[V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta.\]

This becomes the expression for the double integral.

Definition: The double integral in polar coordinates

The double integral of the function \(f(r, \theta)\) over the polar rectangular region \(R\) in the \(r\theta\)-plane is defined as

\[\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[5pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align}\]

Again, just as in section on Double Integrals over Rectangular Regions, the double integral over a polar rectangular region can be expressed as an iterated integral in polar coordinates. Hence,

\[\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta.\]

Notice that the expression for \(dA\) is replaced by \(r \, dr \, d\theta\) when working in polar coordinates. Another way to look at the polar double integral is to change the double integral in rectangular coordinates by substitution. When the function \(f\) is given in terms of \(x\) and \(y\) using \(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), and \(dA = r \, dr \, d\theta\) changes it to

\[\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta.\]

Note that all the properties listed in section on Double Integrals over Rectangular Regions for the double integral in rectangular coordinates hold true for the double integral in polar coordinates as well, so we can use them without hesitation.

Example \(\PageIndex{1A}\): Sketching a Polar Rectangular Region

Sketch the polar rectangular region

\[R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber\]

Solution

As we can see from Figure \(\PageIndex{3}\), \(r = 1\) and \(r = 3\) are circles of radius 1 and 3 and \(0 \leq \theta \leq \pi\) covers the entire top half of the plane. Hence the region \(R\) looks like a semicircular band.

Figure \(\PageIndex{3}\): The polar region \(R\) lies between two semicircles.

Now that we have sketched a polar rectangular region, let us demonstrate how to evaluate a double integral over this region by using polar coordinates.

Example \(\PageIndex{1B}\): Evaluating a Double Integral over a Polar Rectangular Region

Evaluate the integral \(\displaystyle \iint_R 3x \, dA\) over the region \(R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.\)

Solution

First we sketch a figure similar to Figure \(\PageIndex{3}\), but with outer radius \(r=2\). From the figure we can see that we have

\[\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta &\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta+0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta &\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta = 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}\]

Exercise \(\PageIndex{1}\)

Sketch the region \(D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}\), and evaluate \(\displaystyle \iint_R x \, dA\).

Hint

Follow the steps in Example \(\PageIndex{1A}\).

Answer

\(\frac{14}{3}\)

Example \(\PageIndex{2A}\): Evaluating a Double Integral by Converting from Rectangular Coordinates

Evaluate the integral

\[\iint_R (1 - x^2 - y^2) \,dA \nonumber\]

where \(R\) is the unit circle on the \(xy\)-plane.

Solution

The region \(R\) is a unit circle, so we can describe it as \(R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}\).

Using the conversion \(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), and \(dA = r \, dr \, d\theta\), we have

\[\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta = \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta = \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}\]

Example \(\PageIndex{2B}\): Evaluating a Double Integral by Converting from Rectangular Coordinates

Evaluate the integral \[\displaystyle \iint_R (x + y) \,dA \nonumber\] where \(R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.\)

Solution

We can see that \(R\) is an annular region that can be converted to polar coordinates and described as \(R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}\) (see the following graph).

Figure \(\PageIndex{4}\): The annular region of integration \(R\).

Hence, using the conversion \(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), and \(dA = r \, dr \, d\theta\), we have

\[\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\&= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}\]

Exercise \(\PageIndex{2}\)

Evaluate the integral \[ \displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber\] where \(R\) is the circle of radius 2 on the \(xy\)-plane.

Hint

Follow the steps in the previous example.

Answer

\(8\pi\)

General Polar Regions of Integration

To evaluate the double integral of a continuous function by iterated integrals over general polar regions, we consider two types of regions, analogous to Type I and Type II as discussed for rectangular coordinates in section on Double Integrals over General Regions. It is more common to write polar equations as \(r = f(\theta)\) than \(\theta = f(r)\), so we describe a general polar region as \(R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\) (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): A general polar region between \(\alpha < \theta < \beta\) and \(h_1(\theta) < r < h_2(\theta)\).

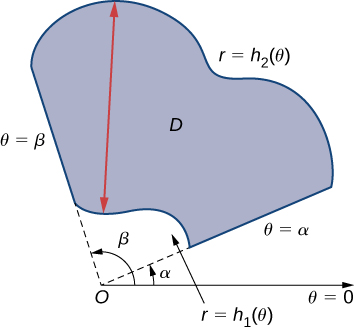
Theorem: Double Integrals over General Polar Regions

If \(f(r, \theta)\) is continuous on a general polar region \(D\) as described above, then

\[\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta.\]

Example \(\PageIndex{3}\): Evaluating a Double Integral over a General Polar Region

Evaluate the integral

\[\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber\]

where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \, \theta\).

Solution

We can describe the region \(D\) as \(\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\} \) as shown in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\): The region \(D\) is the top half of a cardioid.

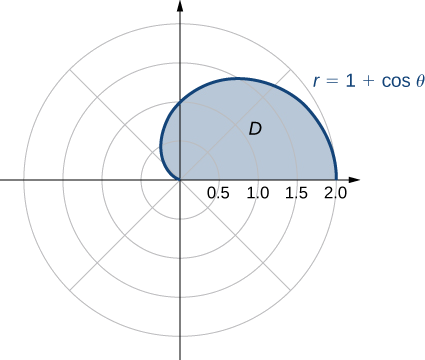
Hence, we have

\[\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\&= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ & = \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ & = - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}\]

Exercise \(\PageIndex{3}\)

Evaluate the integral

\[\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber\]

where \(D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}\).

Hint

Graph the region and follow the steps in the previous example.

Answer

\(\frac{\pi}{8}\)

Polar Areas and Volumes

As in rectangular coordinates, if a solid \(S\) is bounded by the surface \(z = f(r, \theta)\), as well as by the surfaces \(r = a, \, r = b, \, \theta = \alpha\), and \(\theta = \beta\), we can find the volume \(V\) of \(S\) by double integration, as

\[V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta.\]

If the base of the solid can be described as \(D = {(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)}\), then the double integral for the volume becomes

\[V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta.\]

We illustrate this idea with some examples.

Example \(\PageIndex{4A}\): Finding a Volume Using a Double Integral

Find the volume of the solid that lies under the paraboloid \(z = 1 - x^2 - y^2\) and above the unit circle on the \(xy\)-plane (Figure \(\PageIndex{7}\)).

Figure \(\PageIndex{7}\): Finding the volume of a solid under a paraboloid and above the unit circle.

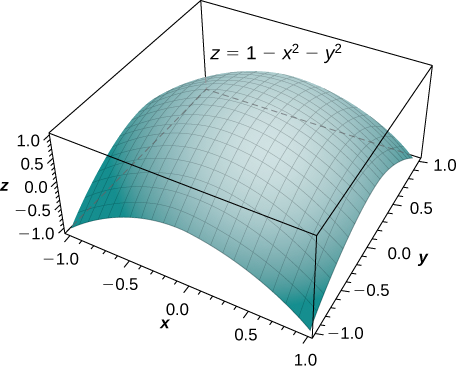
Solution

By the method of double integration, we can see that the volume is the iterated integral of the form \(\displaystyle \iint_R (1 - x^2 - y^2)\,dA\) where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}\).

This integration was shown before in Example, so the volume is \(\frac{\pi}{2}\) cubic units.

Example \(\PageIndex{4B}\): Finding a Volume Using Double Integration

Find the volume of the solid that lies under the paraboloid \(z = 4 - x^2 - y^2\) and above the disk \((x - 1)^2 + y^2 = 1\) on the \(xy\)-plane. See the paraboloid in Figure \(\PageIndex{8}\) intersecting the cylinder \((x - 1)^2 + y^2 = 1\) above the \(xy\)-plane.

Figure \(\PageIndex{8}\): Finding the volume of a solid with a paraboloid cap and a circular base.

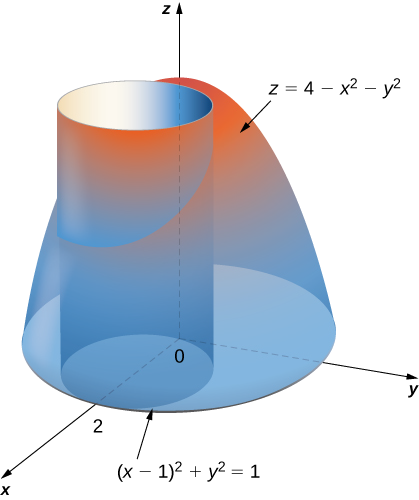
Solution

First change the disk \((x - 1)^2 + y^2 = 1\) to polar coordinates. Expanding the square term, we have \(x^2 - 2x + 1 + y^2 = 1\). Then simplify to get \(x^2 + y^2 = 2x\), which in polar coordinates becomes \(r^2 = 2r \, \cos \, \theta\) and then either \(r = 0\) or \(r = 2 \, \cos \, \theta\). Similarly, the equation of the paraboloid changes to \(z = 4 - r^2\). Therefore we can describe the disk \((x - 1)^2 + y^2 = 1\) on the \(xy\) -plane as the region

\[D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber\]

Hence the volume of the solid bounded above by the paraboloid \(z = 4 - x^2 - y^2\) and below by \(r = 2 \, \cos \theta\) is

\[\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\&= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\&= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^2\theta]\,d\theta = \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}\]

Notice in the next example that integration is not always easy with polar coordinates. Complexity of integration depends on the function and also on the region over which we need to perform the integration. If the region has a more natural expression in polar coordinates or if \(f\) has a simpler antiderivative in polar coordinates, then the change in polar coordinates is appropriate; otherwise, use rectangular coordinates.

Example \(\PageIndex{5A}\): Finding a Volume Using a Double Integral

Find the volume of the region that lies under the paraboloid \(z = x^2 + y^2\) and above the triangle enclosed by the lines \(y = x, \, x = 0\), and \(x + y = 2\) in the \(xy\)-plane.

Solution

First examine the region over which we need to set up the double integral and the accompanying paraboloid.

Figure \(\PageIndex{9}\): Finding the volume of a solid under a paraboloid and above a given triangle.

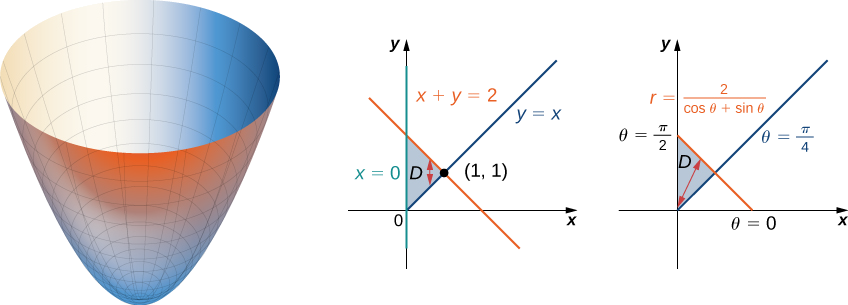
The region \(D\) is \(\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}\). Converting the lines \(y = x, \, x = 0\), and \(x + y = 2\) in the \(xy\)-plane to functions of \(r\) and \(\theta\) we have \(\theta = \pi/4, \, \theta = \pi/2\), and \(r = 2 / (\cos \, \theta + \sin \, \theta)\), respectively. Graphing the region on the \(xy\)- plane, we see that it looks like \(D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}\). Now converting the equation of the surface gives \(z = x^2 + y^2 = r^2\). Therefore, the volume of the solid is given by the double integral

\[\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ \cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta = \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right) d\theta = \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right) d\theta = 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}\]

As you can see, this integral is very complicated. So, we can instead evaluate this double integral in rectangular coordinates as

\[V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx.\]

Evaluating gives

\[\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx = \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 = \frac{4}{3} \; \text{units}^3. \end{align*}\]

To answer the question of how the formulas for the volumes of different standard solids such as a sphere, a cone, or a cylinder are found, we want to demonstrate an example and find the volume of an arbitrary cone.

Example \(\PageIndex{5B}\): Finding a Volume Using a Double Integral

Use polar coordinates to find the volume inside the cone \(z = 2 - \sqrt{x^2 + y^2}\) and above the \(xy\)-plane.

Solution

The region \(D\) for the integration is the base of the cone, which appears to be a circle on the \(xy\)-plane (Figure \(\PageIndex{10}\)).

Figure \(\PageIndex{10}\): Finding the volume of a solid inside the cone and above the \(xy\)-plane.

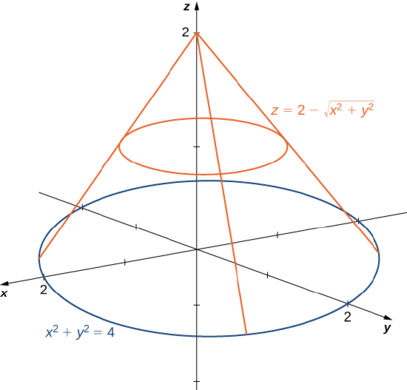
We find the equation of the circle by setting \(z = 0\):

\[\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}\]

This means the radius of the circle is \(2\) so for the integration we have \(0 \leq \theta \leq 2\pi\) and \(0 \leq r \leq 2\). Substituting \(x = r \, \cos \theta\) and \(y = r \, \sin \, \theta\) in the equation \(z = 2 - \sqrt{x^2 + y^2}\) we have \(z = 2 - r\). Therefore, the volume of the cone is

\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber\]

Analysis

Note that if we were to find the volume of an arbitrary cone with radius \(\alpha\) units and height \(h\) units, then the equation of the cone would be \(z = h - \frac{h}{a}\sqrt{x^2 + y^2}\).

We can still use Figure \(\PageIndex{10}\) and set up the integral as

\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber\]

Evaluating the integral, we get \(\frac{1}{3} \pi a^2 h\).

Exercise \(\PageIndex{5}\)

Use polar coordinates to find an iterated integral for finding the volume of the solid enclosed by the paraboloids \(z = x^2 + y^2\) and \(z = 16 - x^2 - y^2\).

Hint

Sketching the graphs can help.

Answer

\[V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber\]

As with rectangular coordinates, we can also use polar coordinates to find areas of certain regions using a double integral. As before, we need to understand the region whose area we want to compute. Sketching a graph and identifying the region can be helpful to realize the limits of integration. Generally, the area formula in double integration will look like

\[\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta.\]

Example \(\PageIndex{6A}\): Finding an Area Using a Double Integral in Polar Coordinates

Evaluate the area bounded by the curve \(r = \cos \, 4\theta\).

Solution

Sketching the graph of the function \(r = \cos \, 4\theta\) reveals that it is a polar rose with eight petals (see the following figure).

Figure \(\PageIndex{11}\): Finding the area of a polar rose with eight petals.

Using symmetry, we can see that we need to find the area of one petal and then multiply it by 8. Notice that the values of \(\theta\) for which the graph passes through the origin are the zeros of the function \(\cos \, 4\theta\), and these are odd multiples of \(\pi/8\). Thus, one of the petals corresponds to the values of \(\theta\) in the interval \([-\pi/8, \pi/8]\). Therefore, the area bounded by the curve \(r = \cos \, 4\theta\) is

\[\begin{align} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\&= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta = 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] = 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align}\]

Example \(\PageIndex{6B}\): Finding Area Between Two Polar Curves

Find the area enclosed by the circle \(r = 3 \, \cos \, \theta\) and the cardioid \(r = 1 + \cos \, \theta\).

Solution

First and foremost, sketch the graphs of the region (Figure \(\PageIndex{12}\)).

Figure \(\PageIndex{12}\): Finding the area enclosed by both a circle and a cardioid.

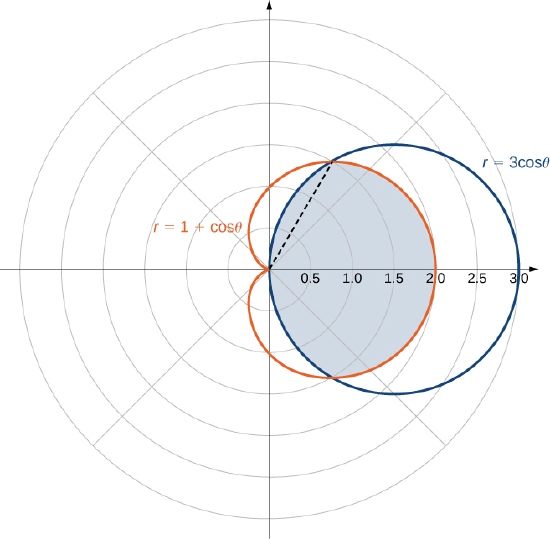
We can from see the symmetry of the graph that we need to find the points of intersection. Setting the two equations equal to each other gives

\[3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber\]

One of the points of intersection is \(\theta = \pi/3\). The area above the polar axis consists of two parts, with one part defined by the cardioid from \(\theta = 0\) to \(\theta = \pi/3\) and the other part defined by the circle from \(\theta = \pi/3\) to \(\theta = \pi/2\). By symmetry, the total area is twice the area above the polar axis. Thus, we have

\[A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber\]

Evaluating each piece separately, we find that the area is

\[A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber\]

Exercise \(\PageIndex{6}\)

Find the area enclosed inside the cardioid \(r = 3 - 3 \, \sin \theta\) and outside the cardioid \(r = 1 + \sin \theta\).

Hint

Sketch the graph, and solve for the points of intersection.

Answer

\[A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber\]

Example \(\PageIndex{7}\): Evaluating an Improper Double Integral in Polar Coordinates

Evaluate the integral

\[\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber\]

Solution

This is an improper integral because we are integrating over an unbounded region \(R^2\). In polar coordinates, the entire plane \(R^2\) can be seen as \(0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty\).

Using the changes of variables from rectangular coordinates to polar coordinates, we have

\[\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\&=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\&= \frac{\pi}{10}. \end{align*}\]

Exercise \(\PageIndex{7}\)

Evaluate the integral

\[\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber\]

Hint

Convert to the polar coordinate system.

Answer

\(\frac{\pi}{4}\)

Key Concepts

• To apply a double integral to a situation with circular symmetry, it is often convenient to use a double integral in polar coordinates. We can apply these double integrals over a polar rectangular region or a general polar region, using an iterated integral similar to those used with rectangular double integrals.
• The area \(dA\) in polar coordinates becomes \(r \, dr \, d\theta\).
• Use \(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), and \(dA = r \, dr \, d\theta\) to convert an integral in rectangular coordinates to an integral in polar coordinates.
• Use \(r^2 = x^2 + y^2\) and \(\theta = tan^{-1} \left(\frac{y}{x}\right)\) to convert an integral in polar coordinates to an integral in rectangular coordinates, if needed.
• To find the volume in polar coordinates bounded above by a surface \(z = f(r, \theta)\) over a region on the \(xy\)-plane, use a double integral in polar coordinates.

Key Equations

• Double integral over a polar rectangular region \(R\)

\[\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber \]

• Double integral over a general polar region

\[\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber\]

Glossary

polar rectangle

the region enclosed between the circles \(r = a\) and \(r = b\) and the angles \(\theta = \alpha\) and \(\theta = \beta\); it is described as \(R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\)

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.