3. Festive Folding
- Page ID
- 13596
This page is a draft and is under active development.
Holiday Decorations (as an excuse to problem solve in geometry!)
References:
- The Mathlab.com, Making the Dice of the Gods, http://www.themathlab.com/wonders/godsdice/godsdice.htm (as of Oct. 6, 2012)
- Aunt Annie’s Crafts, Platonic solids, http://www.auntannie.com/Geometric/PlatonicSolids/ (as if Oct. 6, 2012).
Grade level: This activity can be tailored to various grade levels
Outcomes: Students will construct holiday decorations (really the Platonic solids). A large variety of geometric topics can be built into the lesson and/or discussed afterword. Any platonic solid can be made but I’ll stick to the cube and icosahedrons. The cube because it is geometrically the simplest and makes nice gift boxes and an icosahedron because I think it is visually the most striking.
Motivational strategies:
- The teacher gets to choose the appropriate amount of mathematics to put into the activity and where to put the mathematics in. You can measure angles and lengths, discuss properties of circles and the regular polygons, apply the Pythagorean theorem to build a cube of a particular size, use the law of cosines or sine law to build an icosahedron of a particular size, discuss surface area and of course talk about the Platonic solids and other polyhedra.
Materials/Equipment:
- Cardstock, Bristol board, used greeting cards or some other stuff but not too thick paper. You’ll need lots of it for a class.
- White glue.
Process: You might want to look at the websites in the references to begin to see potential final versions of the decorations and make one or two on your own to get a feeling for time involved and difficulty. They are really just the Platonic solids with or without flaps. Unlike the website descriptions, however, we’ll use a circle cutter to speed the activity along. On the next page, I will outline the directions for making the decorations. After that, I will discuss the potential geometry you can discuss before, after or during the construction of the decorations.
CONSTRUCTION DIRECTIONS:
Step 1: Fix a radius on your circle cutter and mass produce a lot of circles. For example, if students were making cubes they’d need 6 per cube, if they make the icosahedrons they’ll need 20 circles (in my opinion icosahedrons with flaps are the nicest to make!) Keeping the radius fairly small (eg 4 inches on my non-metric circle cutter) would let you get away with using up less paper and makes a nice sized decoration. Produce some extra circles for errors and a geometry discussion with students.
Step 2: Take one of the circles and inscribe the template square (for cubes) or equilateral triangle (for icosahedrons). (Fold to get the center of the circle and for the square, the folds locate the vertices for the square. For the triangle, you can pull out a protractor and measure off 3 120 degree angles to get the vertices.) Cut out the template shape.
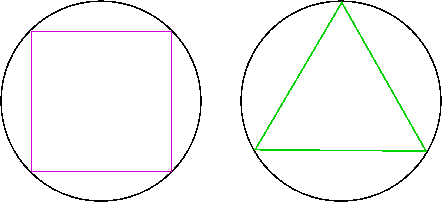
Step 3: Trace this shape and trace it out on as many circles as you need. Work fast – slight imperfections are ok. Now take a rule and a nail (or something else a little sharp) and quickly trace over the lines to break the surface of the cardstock. Fold the sides up to get little ‘cups’ with a square or triangular base. I have gone through steps one to three and made over 120 circles folded into cups in one hour.
Step 4: Bring nets of the cube and icosahedrons (or pictures from the websites mentioned) to help guide the students in putting the shape together. Students will be gluing the flaps together to form the cube or icosahedrons. You have the options of gluing the flaps out or flaps in. The icosahedrons look really neat with the flaps out. Given them the white glue and lead them through putting it together. Again, make one yourself in advance so you can get a feel for how much guidance your students will need and if they need an older helper to finish it off.
Some ideas for the geometry:
- Before you begin, show students a finished decoration and how it is actually constructed from squares/ equilateral triangles inscribed in circles. Show them a circle cutter and discuss how it works (a compass with a blade is much cooler than a compass with a pencil in it!)
- Give them a blank circle and have them problem solve how to find its center and inscribe a square in it. (Folding will do it). If they know about angles and protractors, ask them how to inscribe an equilateral triangle into it and ask why it works. You have the option (if appropriate for your grade level) to go into the general idea of inscribing regular polygons into circles. The regular n sided polygon can be thought of as made up of n identical triangles each triangle having two sides of length the radius of the circle and angle (360/n) degrees. (See picture below) From here you can get to the formula for the interior angles of a regular polygon.

- For lower grades, you can simply ask them to check the angles are equal (and what they are) and check that the side lengths are the same to confirm we have an equilateral triangle/square.
- Ask: I want to make a cube with side length X what radius should I set the circle cutter to get the cube? You need the Pythagorean Theorem to answer that one! Warning: If your circle cutter is not in metric it is a little ugly. (8.3 inches is harder to explain than 8.3 cm) (See below)
- Ask: I want to make an icosahedron with side length X, what radius should I set the circle cutter to get the equilateral triangles. You need the Law of Cosines or Law of Sines to get that one! (see below)

- You can talk about area and surface area. How much paper was wasted? What is the total surface area of the resulting cube/icosahedrons. (One could always find the area of an equilateral triangle by measuring).
- And of course, you can talk about the Platonic solids as well! In fact you can also construct other polyhedra (the Archimedean solids for example) using this technique. I’d need the Pythagorean theorem to construct a cuboctahedron.
Contributors
Roberta La Haye, Mount Royal University


