3.1.2: Proportions

Last updated
Save as PDF

Page ID: 116771

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

be able to describe proportions and find the missing factor in a proportion
be able to work with proportions involving rates

Ratios, Rates, and Proportions

Definition: Ratio, Rate

We have defined a ratio as a comparison, by division, of two pure numbers or two like denominate numbers. We have defined a rateas a comparison, by division, of two unlike denominate numbers.

Definition: Proportion

A proportion is a statement that two ratios or rates are equal. The following two examples show how to read proportions.

$Three fourths equals six eighths. 3 is to four as six is to eight. 25 miles divided by 1 gallon equals 50 miles divided by 2 gallons. 25 miles is to 1 gallon as 50 miles is to 2 gallons.$

Sample Set A

Write or read each proportion.

$\dfrac{3}{5} = \dfrac{12}{20}$

Solution

3 is to 5 as 12 is to 20

Sample Set A

$\dfrac{\text{10 items}}{\text{5 dollars}} = \dfrac{\text{2 items}}{\text{1 dollar}}$

Solution

10 items is to 5 dollars as 2 items is to 1 dollar

Sample Set A

8 is to 12 as 16 is to 24.

Solution

$\dfrac{8}{12} = \dfrac{16}{24}$

Sample Set A

50 milligrams of vitamin C is to 1 tablet as 300 milligrams of vitamin C is to 6 tablets.

Solution

$\dfrac{50}{1} = \dfrac{300}{6}$

Practice Set A

Write or read each proportion.

$\dfrac{3}{8} = \dfrac{6}{16}$

Answer: 3 is to 8 as 6 is to 16

Practice Set A

$\dfrac{\text{2 people}}{\text{1 window}} = \dfrac{\text{10 people}}{\text{5 windows}}$

Answer: 2 people are to 1 window as 10 people are to 5 windows

Practice Set A

15 is to 4 as 75 is to 20.

Answer: $\dfrac{15}{4} = \dfrac{75}{20}$

Practice Set A

2 plates are to 1 tray as 20 plates are to 10 trays.

Answer: \(\dfrac{\text{2 plates}}{\text{1 tray}} = \dfrac{\text{20 plates}}{\text{10 trays}}

Finding the Missing Factor in a Proportion

Many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specified numbers and one unknown number. It is customary to let a letter, such as $x$, represent the unknown number. An example of such a proportion is

$\dfrac{x}{4} = \dfrac{20}{16}$

This proportion is read as "$x$ is to 4 as 20 is to 16."

There is a method of solving these proportions that is based on the equality of fractions. Recall that two fractions are equivalent if and only if their cross products are equal. For example,

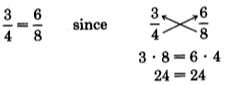
$Three fourths equals six eighths. Next to this equation are the same two fractions, with arrows pointing from the denominators to the opposite fraction's numerator, indicating a cross product. The cross product is 3 times 8 equals 6 times 4, or 24 equals 24.$

Notice that in a proportion that contains three specified numbers and a letter representing an unknown quantity, that regardless of where the letter appears, the following situation always occurs.

$\underbrace{(\text{number}) \cdot (\text{letter}) = (\text{number}) \cdot (\text{number})}_{}$

We recognize this as a multiplication statement. Specifically, it is a missing factor statement. (See [link] for a discussion of multiplication statements.) For example,

$\begin{array} {ll} {\dfrac{x}{4} = \dfrac{20}{16}} & {\text{ means that } 16 \cdot x = 4 \cdot 20} \\ {\dfrac{4}{x} = \dfrac{16}{20}} & {\text{ means that } 4 \cdot 20 = 16 \cdot x} \\ {\dfrac{5}{4} = \dfrac{x}{16}} & {\text{ means that } 5 \cdot 16 = 4 \cdot x} \\ {\dfrac{5}{4} = \dfrac{20}{x}} & {\text{ means that } 5 \cdot x = 4 \cdot 20} \end{array}$

Each of these statements is a multiplication statement. Specifically, each is a missing factor statement. (The letter used here is $x$, whereas $M$ was used in [link].)

Finding the Missing Factor in a Proportion
The missing factor in a missing factor statement can be determined by dividing the product by the known factor, that is, if $x$ represents the missing factor, then

$x = \text{(product)} \div \text{(known factor)}$

Sample Set B

Find the unknown number in each proportion.

$\dfrac{x}{4} = \dfrac{20}{16}$. Find the cross product.

Solution

$\begin{array} {ccll} {16 \cdot x} & = & {20 \cdot 4} & {} \\ {16 \cdot x} & = & {80} & {\text{ Divide the product 80 by the known factor 16.}} \\ {x} & = & {\dfrac{80}{16}} & {} \\ {x} & = & {5} & {\text{ The unkown number is 5.}} \end{array}$

This mean that $\dfrac{5}{4} = \dfrac{20}{16}$, or 5 is to 4 as 20 is to 16.

Sample Set B

$\dfrac{5}{x} = \dfrac{20}{16}$. Find the cross product.

Solution

$\begin{array} {ccll} {5 \cdot 16} & = & {20 \cdot x} & {} \\ {80} & = & {20 \cdot x} & {\text{ Divide the product 80 by the known factor 20.}} \\ {\dfrac{80}{20}} & = & {x} & {} \\ {4} & = & {x} & {\text{ The unkown number is 4.}} \end{array}$

This mean that $\dfrac{5}{4} = \dfrac{20}{16}$, or 5 is to 4 as 20 is to 16.

Sample Set B

$\dfrac{16}{3} = \dfrac{64}{x}$. Find the cross product.

Solution

$\begin{array} {ccll} {16 \cdot x} & = & {64 \cdot 3} & {} \\ {16 \cdot x} & = & {192} & {\text{ Divide 192 by 16.}} \\ {x} & = & {\dfrac{192}{16}} & {} \\ {x} & = & {12} & {\text{ The unkown number is 12.}} \end{array}$

This mean that $\dfrac{16}{3} = \dfrac{64}{12}$, or 16 is to 3 as 64 is to 12.

Sample Set B

$\dfrac{9}{8} = \dfrac{x}{40}$. Find the cross product.

Solution

$\begin{array} {ccll} {9 \cdot 40} & = & {8 \cdot x} & {} \\ {360} & = & {8 \cdot x} & {\text{ Divide 360 by 8.}} \\ {\dfrac{360}{8}} & = & {x} & {} \\ {45} & = & {x} & {\text{ The unkown number is 45.}} \end{array}$

Practice Set B

Find the unknown number in each proportion.

$\dfrac{x}{8} = \dfrac{12}{32}$

Answer: $x = 3$

Practice Set B

$\dfrac{7}{x} = \dfrac{14}{10}$

Answer: $x = 5$

Practice Set B

$\dfrac{9}{11} = \dfrac{x}{55}$

Answer: $x = 45$

Practice Set B

$\dfrac{1}{6} = \dfrac{8}{x}$

Answer: $x = 48$

Proportions Involving Rates

Recall that a rate is a comparison, by division, of unlike denominate numbers. We must be careful when setting up proportions that involve rates. The form is important. For example, if a rate involves two types of units, say unit type 1 and unit type 2, we can write

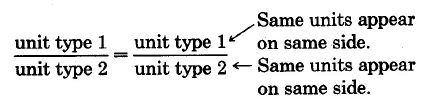
$unit type 1 over unit type 2 equals unit type 1 over unit type 2. The same units appear on the same side, in this case, the same units are part of the same fraction.$

$unit type 1 over unit type 2 equals unit type 1 over unit type 2. The same units appear on the same side, in this case, the same unit is in both denominators and the same unit is in both numerators.$

Both cross products produce a statement of the type

$(\text{unit type 1}) \cdot (\text{unit type 2}) = (\text{unit type 1}) \cdot (\text{unit type 2})$

which we take to mean the comparison

$A comparison of types of units.$

Examples of correctly expressed proportions are the following:

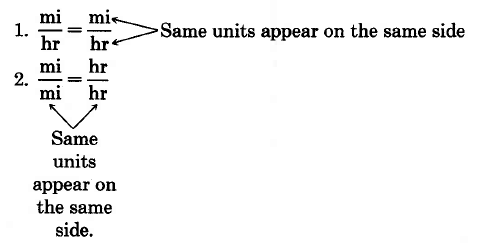
$Two proportions. The first is miles over hr equals miles over hour, where the same unit is always in the denominator. The second is miles over miles equals hours over hours, where the same unit is in its own fraction.$

However, if we write the same type of units on different sides, such as,

$\dfrac{\text{unit type 1}}{\text{unit type 2}} = \dfrac{\text{unit type 2}}{\text{unit type 1}}$

the cross product produces a statement of the form

$A chart showing the comparison of different unit types.$

We can see that this is an incorrect comparison by observing the following example: It is incorrect to write

$\dfrac{\text{2 hooks}}{\text{3 poles}} = \dfrac{\text{6 poles}}{\text{4 hooks}}$

for two reason.

The cross product is numerically wrong: $(2 \cdot 4 \ne 3 \cdot 6)$
The cross product produces the statement “hooks are to hooks as poles are to poles,” which makes no sense.

Exercises

Exercise $\PageIndex{1}$

A statement that two ratios or are equal is called a .

Answer: rates, proportion

For the following 9 problems, write each proportion in fractional form.

Exercise $\PageIndex{2}$

3 is to 7 as 18 is to 42.

Exercise $\PageIndex{3}$

1 is to 11 as 3 is to 33.

Answer: $\dfrac{1}{11} = \dfrac{3}{33}$

Exercise $\PageIndex{4}$

9 is to 14 as 27 is to 42.

Exercise $\PageIndex{5}$

6 is to 90 as 3 is to 45.

Answer: $\dfrac{6}{90} = \dfrac{3}{45}$

Exercise $\PageIndex{6}$

5 liters is to 1 bottle as 20 liters is to 4 bottles.

Exercise $\PageIndex{7}$

18 grams of cobalt is to 10 grams of silver as 36 grams of cobalt is to 20 grams of silver.

Answer: $\dfrac{\text{18 gr cobalt}}{\text{10 gr silver}} = \dfrac{\text{36 gr cobalt}}{\text{20 gr silver}}$

Exercise $\PageIndex{8}$

4 cups of water is to 1 cup of sugar as 32 cups of water is to 8 cups of sugar.

Exercise $\PageIndex{9}$

3 people absent is to 31 people present as 15 people absent is to 155 people present.

Answer: $\dfrac{\text{3 people absent}}{\text{31 people present}} = \dfrac{\text{15 people absent}}{\text{155 people present}}$

Exercise $\PageIndex{10}$

6 dollars is to 1 hour as 90 dollars is to 15 hours.

For the following 10 problems, write each proportion as a sentence.

Exercise $\PageIndex{11}$

$\dfrac{3}{4} = \dfrac{15}{20}$

Answer: 3 is to 4 as 15 is to 20

Exercise $\PageIndex{12}$

$\dfrac{1}{8} = \dfrac{5}{40}$

Exercise $\PageIndex{13}$

$\dfrac{\text{3 joggers}}{\text{100 feet}} = \dfrac{\text{6 joggers}}{\text{200 feet}}$

Answer: 3 joggers are to 100 feet as 6 joggers are to 200 feet

Exercise $\PageIndex{14}$

$\dfrac{\text{12 marshmallows}}{\text{3 sticks}} = \dfrac{\text{36 marshmallows}}{\text{9 sticks}}$

Exercise $\PageIndex{15}$

$\dfrac{\text{40 miles}}{\text{80 miles}} = \dfrac{\text{2 gallons}}{\text{4 gallons}}$

Answer: 40 miles are to 80 miles as 2 gallons are to 4 gallons

Exercise $\PageIndex{16}$

$\dfrac{\text{4 couches}}{\text{10 couches}} = \dfrac{\text{2 houses}}{\text{5 houses}}$

Exercise $\PageIndex{17}$

$\dfrac{\text{1 person}}{\text{1 job}} = \dfrac{\text{8 people}}{\text{8 jobs}}$

Answer: 1 person is to 1 job as 8 people are to 8 jobs

Exercise $\PageIndex{18}$

$\dfrac{\text{1 popsicle}}{\text{2 children}} = \dfrac{\dfrac{1}{2} \text{8 popsicle}}{\text{1 child}}$

Exercise $\PageIndex{19}$

$\dfrac{\text{2,000 pounds}}{\text{1 ton}} = \dfrac{\text{60,000 pounds}}{\text{30 tons}}$

Answer: 2,000 pounds are to 1 ton as 60,000 pounds are to 30 tons

Exercise $\PageIndex{20}$

$\dfrac{\text{1 table}}{\text{5 tables}} = \dfrac{\text{2 people}}{\text{10 people}}$

For the following 10 problems, solve each proportion.

Exercise $\PageIndex{21}$

$\dfrac{x}{5} = \dfrac{6}{15}$

Answer: $x = 2$

Exercise $\PageIndex{22}$

$\dfrac{x}{10} = \dfrac{28}{40}$

Exercise $\PageIndex{23}$

$\dfrac{5}{x} = \dfrac{10}{16}$

Answer: $x = 8$

Exercise $\PageIndex{24}$

$\dfrac{13}{x} = \dfrac{39}{60}$

Exercise $\PageIndex{25}$

$\dfrac{1}{3} = \dfrac{x}{24}$

Answer: $x = 8$

Exercise $\PageIndex{26}$

$\dfrac{7}{12} = \dfrac{x}{60}$

Exercise $\PageIndex{27}$

$\dfrac{8}{3} = \dfrac{72}{x}$

Answer: $x = 27$

Exercise $\PageIndex{28}$

$\dfrac{16}{1} = \dfrac{48}{x}$

Exercise $\PageIndex{29}$

$\dfrac{x}{25} = \dfrac{200}{125}$

Answer: $x = 40$

Exercise $\PageIndex{30}$

$\dfrac{65}{30} = \dfrac{x}{60}$

For the following 5 problems, express each sentence as a proportion then solve the proportion.

Exercise $\PageIndex{31}$

5 hats are to 4 coats as $x$ hats are to 24 coats.

Answer: $x = 30$

Exercise $\PageIndex{32}$

$x$ cushions are to 2 sofas as 24 cushions are to 16 sofas.

Exercise $\PageIndex{33}$

1 spacecraft is to 7 astronauts as 5 spacecraft are to $x$ astronauts.

Answer: $x = 35$

Exercise $\PageIndex{34}$

56 microchips are to $x$ circuit boards as 168 microchips are to 3 circuit boards.

Exercise $\PageIndex{35}$

18 calculators are to 90 calculators as $x$ students are to 150 students.

Answer: $x = 30$

Exercise $\PageIndex{36}$

$x$ dollars are to $40,000 as 2 sacks are to 1 sack.

Indicate whether the proportion is true or false.

Exercise $\PageIndex{37}$

$\dfrac{3}{16} = \dfrac{12}{64}$

Answer: true

Exercise $\PageIndex{38}$

$\dfrac{2}{15} = \dfrac{10}{75}$

Exercise $\PageIndex{39}$

$\dfrac{1}{9} = \dfrac{3}{30}$

Answer: false

Exercise $\PageIndex{40}$

$\dfrac{\text{6 knives}}{\text{7 forks}} = \dfrac{\text{12 knives}}{\text{15 forks}}$

Exercise $\PageIndex{41}$

$\dfrac{\text{33 miles}}{\text{1 gallon}} = \dfrac{\text{99 miles}}{\text{3 gallons}}$

Answer: true

Exercise $\PageIndex{42}$

$\dfrac{\text{320 feet}}{\text{5 seconds}} = \dfrac{\text{65 feet}}{\text{1 second}}$

Exercise $\PageIndex{43}$

$\dfrac{\text{35 students}}{\text{70 students}} = \dfrac{\text{1 class}}{\text{2 classes}}$

Answer: true

Exercise $\PageIndex{44}$

$\dfrac{\text{9 ml chloride}}{\text{45 ml chloride}} = \dfrac{\text{1 test tube}}{\text{7 test tubes}}$

Exercises for Review

Exercise $\PageIndex{43}$

([link]) Use the number 5 and 7 to illustrate the commutative property of addition.

Answer: $5 + 7 = 12$
$7 + 5 = 12$

Exercise $\PageIndex{44}$

([link]) Use the numbers 5 and 7 to illustrate the commutative property of multiplication.

Exercise $\PageIndex{43}$

([link]) Find the difference. $\dfrac{5}{14} - \dfrac{3}{22}$.

Answer: $\dfrac{17}{77}$

Exercise $\PageIndex{44}$

([link]) Find the product. $8.06129 \cdot 1,000$.

Exercise $\PageIndex{43}$

([link]) Write the simplified fractional form of the rate “sixteen sentences to two paragraphs.”

Answer: $\dfrac{\text{8 sentences}}{\text{1 paragraph}}$