4.4: Length of a Vector
- Last updated
- Save as PDF
- Page ID
- 72195
Learning Objectives
- Find the length of a vector and the distance between two points in \(\mathbb{R}^n\).
- Find the corresponding unit vector to a vector in \(\mathbb{R}^n\).
In this section, we explore what is meant by the length of a vector in \(\mathbb{R}^n\). We develop this concept by first looking at the distance between two points in \(\mathbb{R}^n\).
First, we will consider the concept of distance for \(\mathbb{R}\), that is, for points in \(\mathbb{R}^1\). Here, the distance between two points \(P\) and \(Q\) is given by the absolute value of their difference. We denote the distance between \(P\) and \(Q\) by \(d(P,Q)\) which is defined as \[d(P,Q) = \sqrt{ \left( P-Q\right) ^{2}} \label{distance1}\]
Consider now the case for \(n=2\), demonstrated by the following picture.
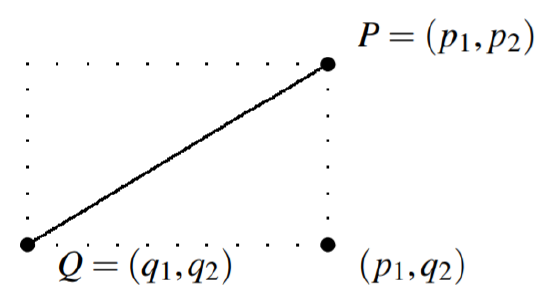
There are two points \(P =\left( p_{1},p_{2}\right)\) and \(Q = \left(q_{1},q_{2}\right)\) in the plane. The distance between these points is shown in the picture as a solid line. Notice that this line is the hypotenuse of a right triangle which is half of the rectangle shown in dotted lines. We want to find the length of this hypotenuse which will give the distance between the two points. Note the lengths of the sides of this triangle are \(\left| p_{1}-q_{1}\right|\) and \(\left| p_{2}-q_{2}\right|\), the absolute value of the difference in these values. Therefore, the Pythagorean Theorem implies the length of the hypotenuse (and thus the distance between \(P\) and \(Q\)) equals \[\left( \left| p_{1}-q_{1}\right| ^{2}+\left| p_{2}-q_{2}\right| ^{2}\right) ^{1/2}=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2} \label{distance2}\]
Now suppose \(n=3\) and let \(P = \left( p_{1},p_{2},p_{3}\right)\) and \(Q = \left( q_{1},q_{2},q_{3}\right)\) be two points in \(\mathbb{R}^{3}.\) Consider the following picture in which the solid line joins the two points and a dotted line joins the points \(\left( q_{1},q_{2},q_{3}\right)\) and \(\left( p_{1},p_{2},q_{3}\right) .\)
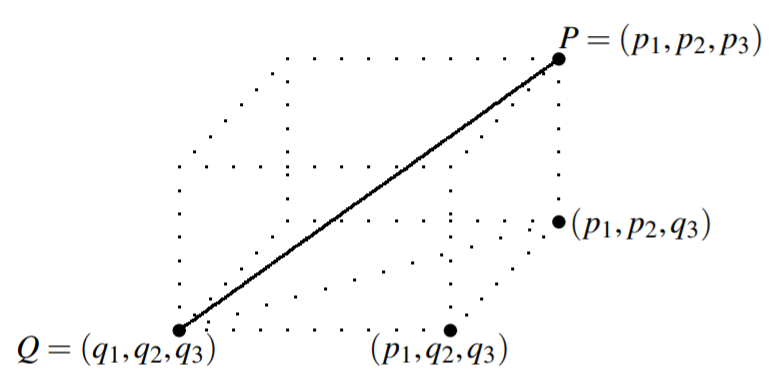
Here, we need to use Pythagorean Theorem twice in order to find the length of the solid line. First, by the Pythagorean Theorem, the length of the dotted line joining \(\left( q_{1},q_{2},q_{3}\right)\) and \(\left( p_{1},p_{2},q_{3}\right)\) equals \[\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\nonumber \] while the length of the line joining \(\left( p_{1},p_{2},q_{3}\right)\) to \(\left( p_{1},p_{2},p_{3}\right)\) is just \(\left| p_{3}-q_{3}\right| .\) Therefore, by the Pythagorean Theorem again, the length of the line joining the points \(P = \left( p_{1},p_{2},p_{3}\right)\) and \(Q = \left( q_{1},q_{2},q_{3}\right)\) equals \[\left( \left( \left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2}\nonumber \] \[=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2} \label{distance3}\]
This discussion motivates the following definition for the distance between points in \(\mathbb{R}^n\).
Definition \(\PageIndex{1}\): Distance Between Points
Let \(P=\left( p_{1},\cdots ,p_{n}\right)\) and \(Q=\left( q_{1},\cdots ,q_{n}\right)\) be two points in \(\mathbb{R}^{n}\). Then the distance between these points is defined as \[\text{ distance between }P\text{ and } Q\text{ } = d( P, Q ) = \left( \sum_{k=1}^{n}\left\vert p_{k}-q_{k}\right\vert ^{2}\right) ^{1/2}\nonumber \] This is called the distance formula. We may also write \(\left\vert P - Q \right\vert\) as the distance between \(P\) and \(Q\).
From the above discussion, you can see that Definition \(\PageIndex{1}\) holds for the special cases \(n=1,2,3\), as in Equations \(\eqref{distance1}\), \(\eqref{distance2}\), \(\eqref{distance3}\). In the following example, we use Definition \(\PageIndex{1}\) to find the distance between two points in \(\mathbb{R}^4\).
Example \(\PageIndex{1}\): Distance Between Points
Find the distance between the points \(P\) and \(Q\) in \(\mathbb{R}^{4}\), where \(P\) and \(Q\) are given by \[P=\left( 1,2,-4,6\right)\nonumber \] and \[Q=\left( 2,3,-1,0\right)\nonumber \]
Solution
We will use the formula given in Definition \(\PageIndex{1}\) to find the distance between \(P\) and \(Q\). Use the distance formula and write \[d(P,Q)= \left( \left( 1-2\right) ^{2}+\left( 2-3\right) ^{2}+\left( -4-\left( -1\right) \right) ^{2}+\left( 6-0\right)^{2}\right) ^{\frac{1}{2}} = 47\nonumber \]
Therefore, \(d( P,Q) = \sqrt{47}.\)
There are certain properties of the distance between points which are important in our study. These are outlined in the following theorem.
Theorem \(\PageIndex{1}\): Properties of Distance
Let \(P\) and \(Q\) be points in \(\mathbb{R}^n\), and let the distance between them, \(d( P, Q)\), be given as in Definition \(\PageIndex{1}\). Then, the following properties hold.
- \(d( P, Q) = d( Q, P)\)
- \(d( P, Q) \geq 0\), and equals 0 exactly when \(P = Q.\)
There are many applications of the concept of distance. For instance, given two points, we can ask what collection of points are all the same distance between the given points. This is explored in the following example.
Example \(\PageIndex{2}\): The Plane Between Two Points
Describe the points in \(\mathbb{R}^3\) which are at the same distance between \(\left( 1,2,3\right)\) and \(\left( 0,1,2\right) .\)
Solution
Let \(P = \left( p_1 , p_2, p_3\right)\) be such a point. Therefore, \(P\) is the same distance from \(\left( 1,2,3\right)\) and \(\left( 0,1,2\right) .\) Then byDefinition \(\PageIndex{1}\), \[\sqrt{\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3-3\right) ^{2}}= \sqrt{\left( p_1 - 0 \right)^{2}+\left( p_2-1\right) ^{2}+\left( p_3-2\right) ^{2}}\nonumber \] Squaring both sides we obtain \[\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3 -3\right) ^{2}=p_1^{2}+\left( p_2-1\right) ^{2}+\left( p_3 -2\right) ^{2}\nonumber \] and so \[ \ p_1^{2}-2p_1+14+p_2^{2}-4p_2+p_3^{2}-6p_3=p_1^{2}+p_2^{2}-2p_2+5+p_3^{2}-4p_3\nonumber \] Simplifying, this becomes \[-2p_1+14-4p_2-6p_3=-2p_2+5-4p_3\nonumber \] which can be written as \[2p_1+2p_2+2p_3=-9 \label{distanceplane}\] Therefore, the points \(P = \left( p_1,p_2,p_3\right)\) which are the same distance from each of the given points form a plane whose equation is given by \(\eqref{distanceplane}\).
We can now use our understanding of the distance between two points to define what is meant by the length of a vector. Consider the following definition.
Definition \(\PageIndex{2}\): Length of a Vector
Let \(\vec{u} = \left[ u_{1} \cdots u_{n} \right]^T\) be a vector in \(\mathbb{R}^n\). Then, the length of \(\vec{u}\), written \(\| \vec{u} \|\) is given by \[\| \vec{u} \| = \sqrt{ u_{1}^2 + \cdots + u_{n}^2}\nonumber \]
This definition corresponds to Definition \(\PageIndex{1}\), if you consider the vector \(\vec{u}\) to have its tail at the point \(0 = \left( 0, \cdots ,0 \right)\) and its tip at the point \(U = \left(u_1, \cdots, u_n \right)\). Then the length of \(\vec{u}\) is equal to the distance between \(0\) and \(U\), \(d(0,U)\). In general, \(d(P,Q)=||\vec{PQ}||\).
ConsiderExample \(\PageIndex{1}\). ByDefinition \(\PageIndex{2}\), we could also find the distance between \(P\) and \(Q\) as the length of the vector connecting them. Hence, if we were to draw a vector \(\overrightarrow{PQ}\) with its tail at \(P\) and its point at \(Q\), this vector would have length equal to \(\sqrt{47}\).
We conclude this section with a new definition for the special case of vectors of length \(1\).
Definition \(\PageIndex{3}\): Unit Vector
Let \(\vec{u}\) be a vector in \(\mathbb{R}^{n}\). Then, we call \(\vec{u}\) a unit vector if it has length 1, that is if \[\| \vec{u} \| = 1\nonumber \]
Let \(\vec{v}\) be a vector in \(\mathbb{R}^{n}\). Then, the vector \(\vec{u}\) which has the same direction as \(\vec{v}\) but length equal to \(1\) is the corresponding unit vector of \(\vec{v}\). This vector is given by \[\vec{u} = \frac{1}{\| \vec{v} \|} \vec{v}\nonumber \]
We often use the term normalize to refer to this process. When we normalize a vector, we find the corresponding unit vector of length \(1\). Consider the following example.
Example \(\PageIndex{3}\): Finding a Unit Vector
Let \(\vec{v}\) be given by \[\vec{v} = \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T\nonumber \] Find the unit vector \(\vec{u}\) which has the same direction as \(\vec{v}\).
Solution
We will use Definition \(\PageIndex{3}\) to solve this. Therefore, we need to find the length of \(\vec{v}\) which, by Definition \(\PageIndex{2}\) is given by \[\| \vec{v} \| = \sqrt{ v_{1}^2 + v_{2}^2+ v_{3}^2}\nonumber \] Using the corresponding values we find that \[\begin{aligned} \| \vec{v} \| &= \sqrt{ 1^2 + \left(-3 \right)^2 + 4^2} \\ &= \sqrt{ 1 + 9 + 16} \\ &= \sqrt{26} \end{aligned}\] In order to find \(\vec{u}\), we divide \(\vec{v}\) by \(\sqrt{26}\). The result is \[\begin{aligned} \vec{u} &= \frac{1}{\| \vec{v} \|} \vec{v} \\ &= \frac{1}{\sqrt{26}} \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T \\ &= \left[ \begin{array}{rrr} \frac{1}{\sqrt{26}} & -\frac{3}{\sqrt{26}} & \frac{4}{\sqrt{26}} \end{array} \right]^T\end{aligned}\]
You can verify using the Definition \(\PageIndex{1}\) that \(\| \vec{u} \| = 1\).


