4.9: The Cross Product
- Last updated
- Save as PDF
- Page ID
- 72200
Outcomes
- Compute the cross product and box product of vectors in \(\mathbb{R}^3\).
Recall that the dot product is one of two important products for vectors. The second type of product for vectors is called the cross product. It is important to note that the cross product is only defined in \(\mathbb{R}^{3}.\) First we discuss the geometric meaning and then a description in terms of coordinates is given, both of which are important. The geometric description is essential in order to understand the applications to physics and geometry while the coordinate description is necessary to compute the cross product.
Consider the following definition.
Definition \(\PageIndex{1}\): Right Hand System of Vectors
Three vectors, \(\vec{u},\vec{v},\vec{w}\) form a right hand system if when you extend the fingers of your right hand along the direction of vector \(\vec{u}\) and close them in the direction of \(\vec{v}\), the thumb points roughly in the direction of \(\vec{w}\).
For an example of a right handed system of vectors, see the following picture.
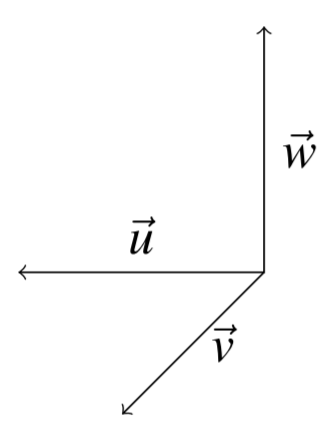
In this picture the vector \(\vec{w}\) points upwards from the plane determined by the other two vectors. Point the fingers of your right hand along \(\vec{u}\), and close them in the direction of \(\vec{v}\). Notice that if you extend the thumb on your right hand, it points in the direction of \(\vec{w}\).
You should consider how a right hand system would differ from a left hand system. Try using your left hand and you will see that the vector \(\vec{w}\) would need to point in the opposite direction.
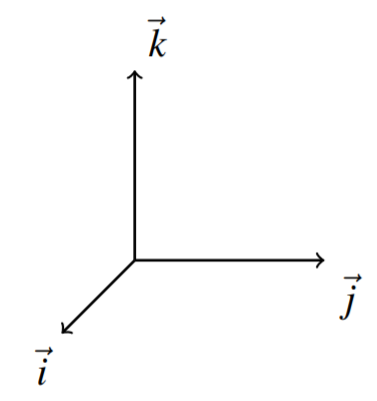
Notice that the special vectors, \(\vec{i},\vec{j},\vec{k}\) will always form a right handed system. If you extend the fingers of your right hand along \(\vec{i}\) and close them in the direction \(\vec{j}\), the thumb points in the direction of \(\vec{k}\).
The following is the geometric description of the cross product. Recall that the dot product of two vectors results in a scalar. In contrast, the cross product results in a vector, as the product gives a direction as well as magnitude.
Definition \(\PageIndex{2}\): Geometric Definition of Cross Product
Let \(\vec{u}\) and \(\vec{v}\) be two vectors in \(\mathbb{R}^{3}.\) Then the cross product, written \(\vec{u}\times \vec{v}\), is defined by the following two rules.
- Its length is \[\| \vec{u}\times \vec{v}\| =\| \vec{u}\| \| \vec{v}\| \sin \theta, \nonumber \] where \(\theta\) is the included angle between \(\vec{u}\) and \(\vec{v}\).
- It is perpendicular to both \(\vec{u}\) and \(\vec{v}\), that is \[\left( \vec{u}\times \vec{v} \right) \cdot \vec{u}=0, \]\[\left( \vec{u}\times \vec{v} \right) \cdot \vec{v}=0, \nonumber\] and \[\vec{u},\vec{v},\vec{u}\times \vec{v} \nonumber\] form a right hand system.
The cross product of the special vectors \(\vec{i}, \vec{j}, \vec{k}\) is as follows. \[\begin{array}{cc} \vec{i}\times \vec{j}=\vec{k} & \vec{j}\times \vec{i}=-\vec{k} \\ \vec{k}\times \vec{i}=\vec{j} & \vec{i}\times \vec{k}=-\vec{j} \\ \vec{j}\times \vec{k}=\vec{i} & \vec{k}\times \vec{j}=-\vec{i} \end{array}\nonumber \] With this information, the following gives the coordinate description of the cross product.
Recall that the vector \(\vec{u}= \left[ \begin{array}{ccc} u_1 & u_2 & u_3 \end{array} \right]^T\) can be written in terms of \(\vec{i}, \vec{j}, \vec{k}\) as \(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\).
Theorem \(\PageIndex{1}\): Coordinate Description of Cross Product
Let \(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\) and \(\vec{v}=v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\) be two vectors. Then
\[\begin{array}{c} \vec{u}\times \vec{v} =\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3} - u_{3}v_{1}\right) \vec{j}+ \left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \label{crossprod1} \end{array}\]
Writing \(\vec{u} \times \vec{v}\) in the usual way, it is given by
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} u_{2}v_{3}-u_{3}v_{2} \\ -(u_{1}v_{3}-u_{3}v_{1}) \\ u_{1}v_{2}-u_{2}v_{1} \end{array} \right]\nonumber \]
We now prove this proposition.
- Proof
-
From the above table and the properties of the cross product listed, \[\begin{aligned} \vec{u} \times \vec{v} &= \left( u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\right) \times \left( v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\right) \\ &= u_{1}v_{2}\vec{i}\times \vec{j}+u_{1}v_{3}\vec{i}\times \vec{k}+u_{2}v_{1}\vec{j}\times \vec{i}+ u_{2}v_{3}\vec{j}\times \vec{k}+ +u_{3}v_{1}\vec{k}\times \vec{i}+u_{3}v_{2}\vec{k}\times \vec{j} \\ &=u_{1}v_{2}\vec{k}-u_{1}v_{3}\vec{j}-u_{2}v_{1}\vec{k}+u_{2}v_{3} \vec{i}+u_{3}v_{1}\vec{j}-u_{3}v_{2}\vec{i} \\ &=\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}+\left( u_{3}v_{1}-u_{1}v_{3}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \end{aligned}\] \[\label{crossprod2}\]
There is another version of \(\eqref{crossprod1}\) which may be easier to remember. We can express the cross product as the determinant of a matrix, as follows.
\[\vec{u}\times \vec{v} = \left\vert \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{array} \right\vert \label{crossprod3}\] Expanding the determinant along the top row yields \[\vec{i}\left( -1\right) ^{1+1}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert +\vec{j}\left( -1\right) ^{2+1}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left( -1\right) ^{3+1}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber \]\
\[=\vec{i}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert -\vec{j}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber \]
Expanding these determinants leads to \[\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3}-u_{3}v_{1}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \nonumber \] which is the same as \(\eqref{crossprod2}\).
The cross product satisfies the following properties.
Proposition \(\PageIndex{1}\): Properties of the Cross Product
Let \(\vec{u}, \vec{v}, \vec{w}\) be vectors in \(\mathbb{R}^3\), and \(k\) a scalar. Then, the following properties of the cross product hold.
- \(\vec{u}\times \vec{v}= -\left( \vec{v}\times \vec{u}\right), \mbox{and} \; \vec{u}\times \vec{u}=\vec{0}\)
- \(\left( k \vec{u}\right)\times \vec{v}= k \left( \vec{u}\times \vec{v}\right) =\vec{u}\times \left( k \vec{v}\right)\)
- \(\vec{u}\times \left( \vec{v}+\vec{w}\right) =\vec{u}\times \vec{v}+\vec{u}\times \vec{w}\)
- \(\left( \vec{v}+\vec{w}\right) \times \vec{u}=\vec{v} \times \vec{u}+\vec{w}\times \vec{u}\)
- Proof
-
Formula \(1.\) follows immediately from the definition. The vectors \(\vec{u}\times \vec{v}\) and \(\vec{v}\times \vec{u}\) have the same magnitude, \(\left\vert \vec{u}\right\vert \left\vert \vec{v}\right\vert \sin \theta ,\) and an application of the right hand rule shows they have opposite direction.
Formula \(2.\) is proven as follows. If \(k\) is a non-negative scalar, the direction of \(\left( k \vec{u}\right) \times \vec{v}\) is the same as the direction of \(\vec{u}\times \vec{v}, k \left( \vec{u}\times \vec{v}\right)\) and \(\vec{u}\times \left( k \vec{v}\right)\). The magnitude is \(k\) times the magnitude of \(\vec{u}\times \vec{v}\) which is the same as the magnitude of \(k \left( \vec{u}\times \vec{v}\right)\) and \(\vec{u}\times \left( k \vec{v}\right) .\) Using this yields equality in \(2\). In the case where \(k <0,\) everything works the same way except the vectors are all pointing in the opposite direction and you must multiply by \(\left\vert k \right\vert\) when comparing their magnitudes.
The distributive laws, \(3.\) and \(4.\), are much harder to establish. For now, it suffices to notice that if we know that \(3.\) is true, \(4.\) follows. Thus, assuming \(3.\), and using \(1.\), \[\begin{aligned} \left( \vec{v}+\vec{w}\right) \times \vec{u}& =-\vec{u}\times \left( \vec{v}+\vec{w}\right) \\ & =-\left( \vec{u}\times \vec{v}+\vec{u}\times \vec{w}\right) \\ & =\vec{v}\times \vec{u}+\vec{w}\times \vec{u}\end{aligned}\]
We will now look at an example of how to compute a cross product.
Example \(\PageIndex{1}\): Find a Cross Product
Find \(\vec{u} \times \vec{v}\) for the following vectors
\[\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber \]
Solution
Note that we can write \(\vec{u}, \vec{v}\) in terms of the special vectors \(\vec{i}, \vec{j}, \vec{k}\) as
\[\begin{array}{c} \vec{u} = \vec{i}-\vec{j}+2\vec{k} \\ \vec{v} = 3\vec{i}-2\vec{j}+\vec{k} \end{array}\nonumber \]
We will use the equation given by \(\eqref{crossprod3}\) to compute the cross product.
\[\vec{u} \times \vec{v} = \left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & -1 & 2 \\ 3 & -2 & 1 \end{array} \right\vert =\left\vert \begin{array}{rr} -1 & 2 \\ -2 & 1 \end{array} \right\vert \vec{i}-\left\vert \begin{array}{rr} 1 & 2 \\ 3 & 1 \end{array} \right\vert \vec{j}+\left\vert \begin{array}{rr} 1 & -1 \\ 3 & -2 \end{array} \right\vert \vec{k}=3\vec{i}+5\vec{j}+\vec{k}\nonumber \]
We can write this result in the usual way, as \[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber \]
An important geometrical application of the cross product is as follows. The size of the cross product, \(\| \vec{u}\times \vec{v}\|\), is the area of the parallelogram determined by \(\vec{u}\) and \(\vec{v}\), as shown in the following picture.
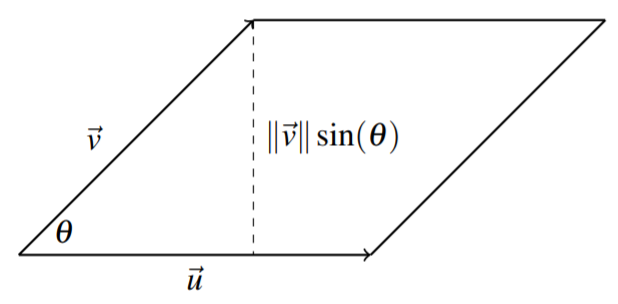
We examine this concept in the following example.
Example \(\PageIndex{2}\): Area of a Parallelogram
Find the area of the parallelogram determined by the vectors \(\vec{u}\) and \(\vec{v}\) given by
\[\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber \]
Solution
Notice that these vectors are the same as the ones given in Example \(\PageIndex{1}\). Recall from the geometric description of the cross product, that the area of the parallelogram is simply the magnitude of \(\vec{u} \times \vec{v}\). From Example \(\PageIndex{1}\), \(\vec{u} \times \vec{v} = 3\vec{i}+5\vec{j}+\vec{k}\). We can also write this as
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber \]
Thus the area of the parallelogram is
\[\| \vec{u} \times \vec{v} \| = \sqrt{(3)(3) + (5)(5) + (1)(1)} = \sqrt{9+25+1}=\sqrt{35}\nonumber \]
We can also use this concept to find the area of a triangle. Consider the following example.
Example \(\PageIndex{3}\): Area of Triangle
Find the area of the triangle determined by the points \(\left(1, 2, 3 \right) , \left( 0,2,5\right), \left( 5,1, 2 \right)\)
Solution
This triangle is obtained by connecting the three points with lines. Picking \(\left( 1,2,3\right)\) as a starting point, there are two displacement vectors, \(\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T\) and \(\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T\). Notice that if we add either of these vectors to the position vector of the starting point, the result is the position vectors of the other two points. Now, the area of the triangle is half the area of the parallelogram determined by \(\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T\) and \(\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T.\) The required cross product is given by
\[\left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right] \times \left[ \begin{array}{r} 4 \\ -1 \\ -1 \end{array} \right] = \left[ \begin{array}{rrr} 2 & 7 & 1 \end{array} \right]\nonumber \]
Taking the size of this vector gives the area of the parallelogram, given by
\[\sqrt{(2)(2) + (7)(7) + (1)(1)} = \sqrt{4+49+1} = \sqrt{54}\nonumber \] Hence the area of the triangle is \(\frac{1}{2}\sqrt{54}= \frac{3}{2}\sqrt{6}.\)
In general, if you have three points in \(\mathbb{R}^{3}, P,Q,R\), the area of the triangle is given by \[\frac{1}{2}\| \vec{PQ} \times \vec{PR} \|\nonumber \]
Recall that \(\vec{PQ}\) is the vector running from point \(P\) to point \(Q\).
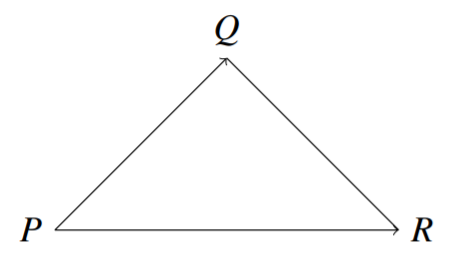
In the next section, we explore another application of the cross product.
The Box Product
Recall that we can use the cross product to find the the area of a parallelogram. It follows that we can use the cross product together with the dot product to find the volume of a parallelepiped. We begin with a definition.
Definition \(\PageIndex{3}\): Parallelepiped
A parallelepiped determined by the three vectors, \(\vec{u},\vec{v}\), and \(\vec{w}\) consists of \[\left\{ r\vec{u}+s\vec{v}+t\vec{w}:r,s,t\in \left[ 0,1\right] \right\}\nonumber \]
That is, if you pick three numbers, \(r,s,\) and \(t\) each in \(\left[ 0,1\right]\) and form \(r\vec{u}+s\vec{v}+t\vec{w}\) then the collection of all such points makes up the parallelepiped determined by these three vectors.
The following is an example of a parallelepiped.
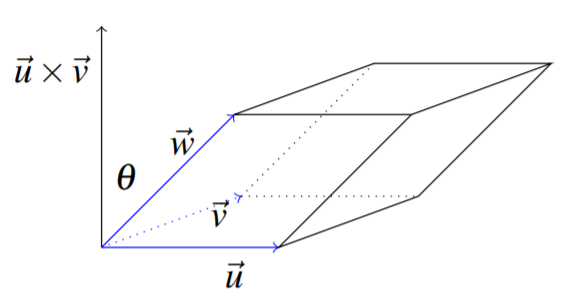
Notice that the base of the parallelepiped is the parallelogram determined by the vectors \(\vec{u}\) and \(\vec{v}\). Therefore, its area is equal to \(\| \vec{u}\times \vec{v} \|\). The height of the parallelepiped is \(\| \vec{w}\| \cos \theta\) where \(\theta\) is the angle shown in the picture between \(\vec{w}\) and \(\vec{u}\times \vec{v}\). The volume of this parallelepiped is the area of the base times the height which is just \[\| \vec{u}\times \vec{v}\| \| \vec{w}\| \cos \theta = \left( \vec{u}\times\vec{v}\right) \cdot \vec{w}\nonumber \] This expression is known as the box product and is sometimes written as \(\left[ \vec{u},\vec{v},\vec{w}\right] .\) You should consider what happens if you interchange the \(\vec{v}\) with the \(\vec{w}\) or the \(\vec{u}\) with the \(\vec{w}\). You can see geometrically from drawing pictures that this merely introduces a minus sign. In any case the box product of three vectors always equals either the volume of the parallelepiped determined by the three vectors or else \(-1\) times this volume.
Proposition \(\PageIndex{2}\): The Box Product
Let \(\vec{u}, \vec{v}, \vec{w}\) be three vectors in \(\mathbb{R}^n\) that define a parallelepiped. Then the volume of the parallelepiped is the absolute value of the box product, given by \[\left| \left(\vec{u}\times\vec{v}\right) \cdot \vec{w} \right|\nonumber \]
Consider an example of this concept.
Example \(\PageIndex{4}\): Volume of a Parallelepiped
Find the volume of the parallelepiped determined by the vectors
\[\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right], \vec{w} = \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right]\nonumber \]
Solution
According to the above discussion, pick any two of these vectors, take the cross product and then take the dot product of this with the third of these vectors. The result will be either the desired volume or \(-1\) times the desired volume. Therefore by taking the absolute value of the result, we obtain the volume.
We will take the cross product of \(\vec{u}\) and \(\vec{v}\). This is given by
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right] \times \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right]\nonumber \] \[=\left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & 2 & -5 \\ 1 & 3 & -6 \end{array} \right\vert = 3\vec{i}+\vec{j}+\vec{k} = \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right]\nonumber \]
Now take the dot product of this vector with \(\vec{w}\) which yields \[\begin{aligned} (\vec{u} \times \vec{v}) \cdot \vec{w} &= \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right] \cdot \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right] \\ &=\left( 3\vec{i}+\vec{j}+\vec{k}\right) \cdot \left( 3\vec{i}+2\vec{j}+3\vec{k}\right) \\ &=9+2+3 \\ &=14\end{aligned}\]
This shows the volume of this parallelepiped is 14 cubic units.
There is a fundamental observation which comes directly from the geometric definitions of the cross product and the dot product.
Proposition \(\PageIndex{3}\): Order of the Product
Let \(\vec{u},\vec{v}\), and \(\vec{w}\) be vectors. Then \(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}=\vec{u}\cdot \left( \vec{v}\times \vec{w} \right) .\)
- Proof
-
This follows from observing that either \(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}\) and \(\vec{u}\cdot \left( \vec{v}\times \vec{w}\right)\) both give the volume of the parallelepiped or they both give \(-1\) times the volume.
Recall that we can express the cross product as the determinant of a particular matrix. It turns out that the same can be done for the box product. Suppose you have three vectors, \(\vec{u}=\left[ \begin{array}{rrr} a & b & c \end{array} \right]^T ,\vec{v}=\left[ \begin{array}{rrr} d & e & f \end{array} \right]^T ,\) and \(\vec{w}=\left[ \begin{array}{rrr} g & h & i \end{array} \right]^T .\) Then the box product \(\vec{u}\cdot \left(\vec{v}\times \vec{w}\right)\) is given by the following. \[\begin{aligned} \vec{u}\cdot \left(\vec{v}\times \vec{w}\right) &= \left[ \begin{array}{r} a \\ b \\ c \end{array} \right] \cdot \left| \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ d & e & f \\ g & h & i \end{array} \right| \\ &=a\left| \begin{array}{rr} e & f \\ h & i \end{array} \right| -b\left| \begin{array}{rr} d & f \\ g & i \end{array} \right| +c\left| \begin{array}{rr} d & e \\ g & h \end{array} \right| \\ &= \det \left[ \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \right] \end{aligned}\]
To take the box product, you can simply take the determinant of the matrix which results by letting the rows be the components of the given vectors in the order in which they occur in the box product.
This follows directly from the definition of the cross product given above and the way we expand determinants. Thus the volume of a parallelepiped determined by the vectors \(\vec{u},\vec{v},\vec{w}\) is just the absolute value of the above determinant.


