5.9.1: Tree Traversal
- Page ID
- 18841
Definition
An ordered rooted tree is a rooted tree in which the children of each internal vertex have an order (generally from left to right).
investigate!
Create an ordered rooted tree for the expression \(3(y-z)^2+\frac{4-x}{2}\). Each vertex should either be assigned a number or an operation.
Mathematical expressions can be ambiguous (as many internet memes show), and the ambiguity can be removed by strict adherence to an order of operations or by complete use of parentheses (called infix notation). There are other ways of writing expressions; we will also consider prefix and postfix notation. Each of these ways of writing a mathematical expression can be derived from an ordered rooted tree for that expression.
Tree traversal algorithms
Definition
A tree traversal algorithm is a method for systematically visiting every vertex of an ordered rooted tree.
We discuss three such algorithms below.
preorder traversal algorithm
- Input: \(T\), an ordered rooted tree with root \(r\)
- Return \(r\)
- For each child \(v\) of \(r\), from left to right:
- Traverse subtree of \(T\) with root \(v\) using preorder
postorder traversal algorithm
- Input: \(T\), an ordered rooted tree with root \(r\)
- For each child \(v\) of \(r\), from left to right:
- Traverse subtree of \(T\) with root \(v\) using postorder
- Return \(r\)
Inorder traversal algorithm
- Input: \(T\), an ordered rooted tree with root \(r\)
- If \(r\) is a leaf, then return \(r\)
- Else, let \(L\) be the leftmost child of \(r\)
- Traverse subtree of \(T\) with root \(L\) using inorder
- Return \(r\)
- For each child \(v\) of \(r\) except \(L\) from left to right:
- Traverse subtree of \(T\) with root \(v\) using inorder
Exercise \(\PageIndex{1}\)
Determine the preorder, inorder, and postorder traversals of the ordered rooted tree below.
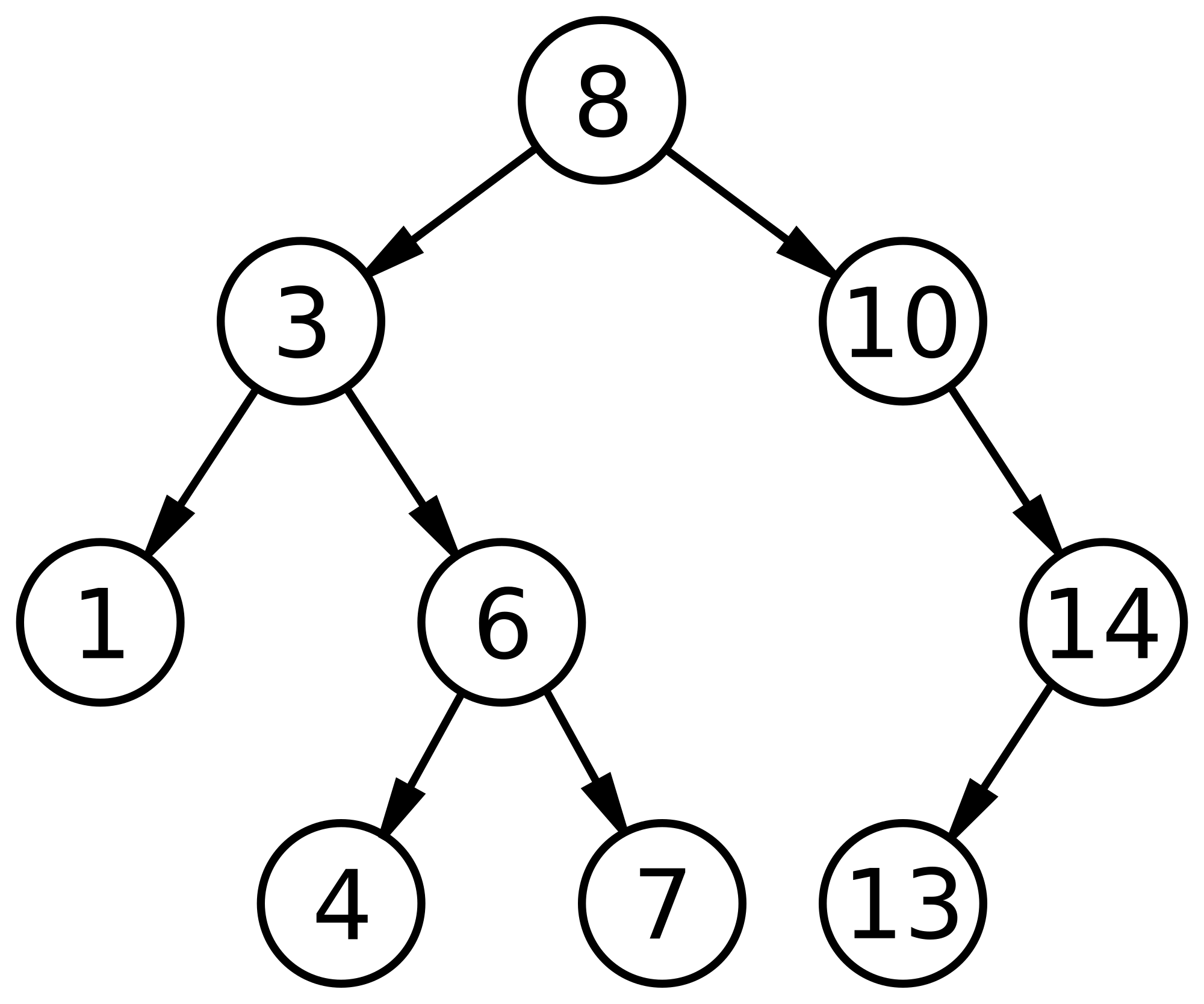
- Answer
-
Preorder: 8, 3, 1, 6, 4, 7, 10, 14, 13
Inorder: 1, 3, 4, 6, 7, 8, 13, 14, 10
Postorder: 1, 4, 7, 6, 3, 13, 14, 10, 8
In fact, there is a simpler way to determine these traversals. First, draw a closed curve around the rooted tree, hugging both sides of each edge. To get the preorder traversal, simply list each vertex the first time it is passed. For postorder, list the vertices the last time they are passed. For inorder, list leaves the first time they are passed and internal vertices the second time.
Exercise \(\PageIndex{2}\)
Determine the prefix form and postfix form of the mathematical expression above by traversing the ordered rooted tree you created in preorder and postorder, respectively. Use \(\uparrow\) to denote exponentiation.
Determine the infix form of the expression by traversing the tree in inorder, including all parentheses
To evaluate an expression in prefix form, notice that an operator precedes the numbers it is applied to. Therefore, we can read right to left, and whenever we encounter an operator preceded immediately by two numbers we can perform the operation. Likewise, we can evaluate an expression in postfix form by reading left to right and performing an operation when we encounter an operator immediately preceded by two numbers.
Example \(\PageIndex{1}\)
- Evaluate the following expression written in prefix form: \(-\,+\,*\,4\,3\,5\,/\,\uparrow\, 2\, 2\, 4\).
- Evaluate the following expression written in postfix form: \( 8\,6\,1\,*\,-\,3\,\uparrow\,10\,5\,/\,-\).
Tags recommended by the template: article:topic

