3. Sample Spaces
- Page ID
- 21069
The following topics are included in this series of five videos.
- Introduction to Sample Spaces
- Sample space, example 2
- Sizes of sample spaces and the multiplication principle
- Sizes of sample spaces, example 2
- Sizes of sample spaces, example 3
An outcome is a possible result from an experiment. A sample space is the set of outcomes of an experiment.
Example \(\PageIndex{1}\)
Consider the following experiment. A teacher is choosing the texts for her courses for next fall. There are 4 texts she is considering for Finite Math, 3 texts she is considering for Calculus, and 2 texts she is considering for Analysis. Describe the sample space for this experiment and then determine how many elements are in the sample space.
Solution
Each element in the sample space S consists of 1 textbook for Finite, 1 textbook for Calc, and 1 textbook for Analysis. If we let \(S\) be the sample space, then \(S=F\times C\times A\) where \(F\) is the set of finite textbooks, \(C\) is the set of calc textbooks, and \(A\) is the set of analysis textbooks. Then \(n(S)=4\times 3\times 2=24\).
The sample space is \(S=\{RR, RPRPP, RPP, PRR, PRPRPP, PRPP, PP\}\).
The sample space is \(S=\{WWW, WWT, WWL, WT, WL, T, LW, LT, LLW, LLT, LLL\}\).
PREWORK:
- Consider the following experiment. A caterer offers 6 appetizers, 4 entrees, and 5 desserts. A menu consists of an appetizer, an entree, and a dessert. A customer chooses a menu for the big party to celebrate her 19th birthday. What is the size of the sample space for this experiment? (In other words, how many different menus are possible?)
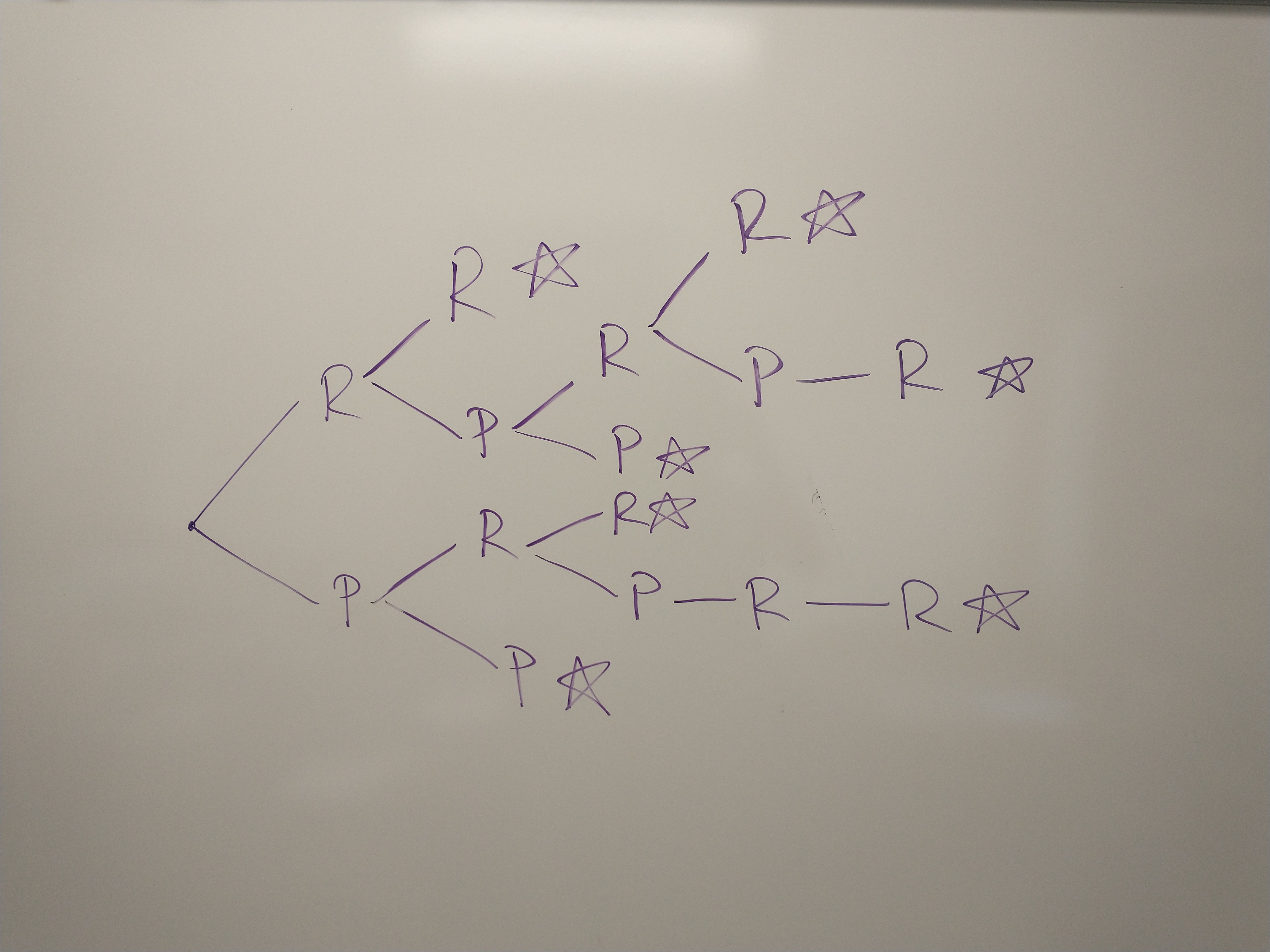
- A jar contains three red and two purple balls. Balls are selected one after the other without replacement until two consecutive balls of the same color are chosen or the jar is empty. Draw a tree diagram and write the sample space for this experiment.
Solutions
1. This experiment has three stages (appetizer, entree, dessert) and the choice made in any one stage doesn't affect the number of choices at any other stage. Therefore we can use the multiplication principle to get \(6\cdot 4\cdot 5=120\) different menus.
2. The tree diagram is below. The sample space is \(S=\{RR, RPRR, RPRPR, RPP, PRR, PRPRR, PP\}\).