5.9.2: Spanning Tree Algorithms
- Page ID
- 18868
Definition
Given a connected graph \(G\), a spanning tree of \(G\) is a subgraph of \(G\) which is a tree and includes all the vertices of \(G\).
We also provided the ideas of two algorithms to find a spanning tree in a connected graph.
Start with the graph connected graph \(G\). If there is no cycle, then the \(G\) is already a tree and we are done. If there is a cycle, let \(e\) be any edge in that cycle and consider the new graph \(G_1=G−e\) (i.e., the graph you get by deleting \(e\)). This tree is still connected since \(e\) belonged to a cycle, there were at least two paths between its incident vertices. Now repeat: if \(G_1\) has no cycles, we are done, otherwise define \(G_2\) to be \(G_1−e_1\), where \(e_1\) is an edge in a cycle in \(G_1\). Keep going. This process must eventually stop, since there are only a finite number of edges to remove. The result will be a tree, and since we never removed any vertex, a spanning tree.
This is by no means the only algorithm for finding a spanning tree. You could have started with the empty graph and added edges that belong to \(G\) as long as adding them would not create a cycle. You have some choices as to which edges you add first: you could always add an edge adjacent to edges you have already added (after the first one, of course), or add them using some other order. Which spanning tree you end up with depends on these choices.
We now provide two algorithms that follow this latter idea of starting with an empty graph and adding edges until we have formed a tree.
Depth-first search algorithm
- Input \(G\), a connected graph with vertices \(v_1,v_2,\ldots,v_n\)
- Let \(T:=\)tree with no edges and only the vertex \(v_1\)
- \(visit(v_1)\) (i.e. apply the procedure \(visit\) to \(v_1\))
VISIT
- Input \(v\), a vertex of a graph \(G\)
- For each vertex \(w\) adjacent to \(v\) and not yet in \(T\)
- add vertex \(w\) and edge \(\{v,w\}\) to \(T\)
- \(visit(w)\)
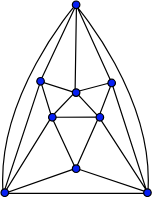
Notice that we can pick our starting vertex arbitrarily and adjacent vertices in any order. Label the vertices in the graph below, pick a starting vertex, and use depth-first search to find a spanning tree of the graph below.
Breadth-first search algorithm
- Input \(G\), a connected graph with vertices \(v_1,v_2,\ldots,v_n\)
- Let \(T:=\)tree with no edges and only the vertex \(v_1\)
- Let \(L:=\)empty list
- Put \(v_1\) in \(L\), a list of unprocessed vertices
- While \(L\) is not empty
- remove the first vertex \(v\) from \(L\)
- for each neighbor \(w\) of \(v\)
- if \(w\) is not in \(L\) and not in \(T\)
- add \(w\) to the end of the list \(L\)
- add \(w\) and the edge \(\{v,w\}\) to \(T\)
- if \(w\) is not in \(L\) and not in \(T\)
Using the same graph, same labels, and same starting vertex, apply the breadth-first search algorithm to find a spanning tree of the graph above.
Find a big-O estimate of the number of steps these algorithms require.
Spanning trees in weighted graphs
In the graph below, there is an oil well located at the left-most vertex, while other vertices represent storage facilities.
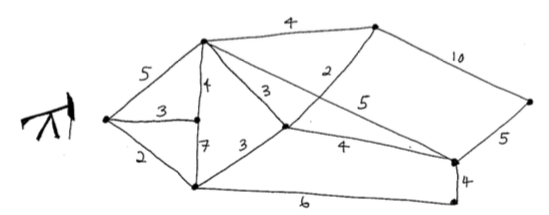
- Suppose the edges represent the possible pipelines we could build, and the weight on an edge represents the cost of building that edge (in millions of dollars). Which pipelines should we build so that we can transport oil from the well to each storage facility, but we want to spend as little money as possible? What is the total cost of building these pipelines? Describe an algorithm that could be used to solve this problem.
- Again, suppose the edges represent the possible pipelines we could build. Now suppose that the weight on each edge represents the time it takes for oil to get through that section of the pipeline (in hours). Which pipelines should we build so that we can transport oil from the well to each storage facility as quickly as possible? Describe an algorithm that could be used to solve this problem.
Definition
A minimum spanning tree in a connected weighted graph is a spanning tree with minimum possible total edge weight.
A shortest path spanning tree from v in a connected weighted graph is a spanning tree such that the distance from \(v\) to any other vertex \(u\) is as small as possible.
We present below two common algorithms used to find minimum spanning trees.
Prim's algorithm
- Input: \(G\), a connected weighted graph with \(n\) vertices
- Let \(T:=\)any edge with minimum weight
- for \(i\) from \(1\) to \(n-2\)
- let \(e:=\)an edge of minimum weight among those incident to a vertex in \(T\) that will not form a cycle in \(T\) if added to it
- \(T:=T\cup e\)
- Return \(T\)
Kruskal's algorithm
- Input: \(G\), a connected weighted graph with \(n\) vertices
- Let \(T\) be an empty graph
- for \(i\) from \(1\) to \(n-1\)
- let \(e:=\)an edge in \(G\) of minimum weight among those that do not form a cycle in \(T\) if added to it
- \(T:=T\cup e\)
- Return \(T\)
Notice the difference between the two algorithms. In Prim's edges that are incident to a vertex already in the tree are added, while in Kruskal's the edges that are added need not be incident to a vertex already in the tree.
We now present an algorithm that creates a shortest path spanning tree from a given vertex.
Shortest path spanning tree algorithm
- Input: \(G\), a connected weighted graph with \(n\) vertices \(v_1,v_2,\ldots,v_n\)and with source vertex \(v_1\)
- Apply Dijkstra's algorithm (Section 5.7) to \(G\)
- Let \(T\) be an empty graph
- For \(i\) from \(2\) to \(n\)
- Add edge \(e=\{v_i,prev(v_i)\}\) to \(T\)
- Return \(T\)

