Addition as combining
For now, we’ll focus on the base-10 system. Here’s how we think about the number 273 in that system:
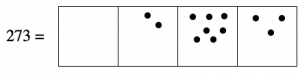
And here is the number 512:

273+512
We can add these in the natural way: just combine the piles of dots. Since they’re already in place-value columns, we can combine dots from the two numbers that are in the same place-value box.
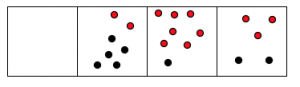
We can count up the answer: there are 7 dots in the hundreds box, 8 dots in the tens box, and 5 dots in the ones box.
\[\begin{split} 273& \\ +\; 512 \\ \hline 785& \end{split} \nonumber \]
And saying out the long way we have:
- Two hundreds plus five hundreds gives 7 hundreds.
- Seven tens plus one ten gives 8 tens.
- Three ones plus two ones gives 5 ones.
This gives the answer: 785.
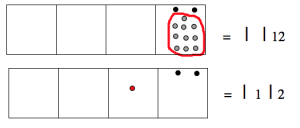
: 163+489
Let’s do another one. Consider 163+489.
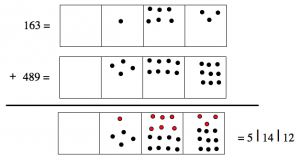
\[\begin{split} 1\; \; \; 6\; \; \; 3& \\ +\; 4\; \; \; 8\; \; \; 9& \\ \hline 5 | 14 | 12& \end{split} \nonumber \]
And this is absolutely correct:
- One hundred plus four hundreds is 5 hundreds.
- Six tens plus eight tens is 14 tens.
- Three ones plus nine ones is 12 ones.
The answer is 5 | 14 | 12, which we might try to pronounce as “five hundred and fourteeny-tenty twelvety.” The trouble with this answer is that most of the rest of the world wouldn’t understand what we are talking about.
Since this is a base 10 system, we can do some explosions.

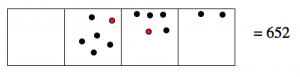
The answer is “six hundred fifty two.” Okay, the world can understand this one!
\[\begin{split} 1\; \; \; 6\; \; \; 3& \\ +\; 4\; \; \; 8\; \; \; 9& \\ \hline 5 | 14 | 12& = 652 \end{split} \nonumber \]
Think / Pair / Share
Solve the following exercises by thinking about the dots and boxes. (You can draw the pictures, or just imagine them.) Then translate the answer into something the rest of the world can understand.
\[\begin{split} 148& \\ +\; 323& \\ \hline \end{split} \qquad \qquad \begin{split} 567& \\ +\; 271& \\ \hline \end{split} \qquad \qquad \begin{split} 310462872& \\ +\; 389107123& \\ \hline \end{split} \nonumber \]
Problem 1
Use the dots and boxes technique to solve these problems. Do not covert to base 10! Try to work directly in the base given. It might help to actually draw the pictures.
\[\begin{split} 20413_{five}& \\ +\; 13244_{five}& \\ \hline \end{split} \qquad \qquad \begin{split} 4052_{nine}& \\ +\; 6288_{nine}& \\ \hline \end{split} \qquad \qquad \begin{split} 3323_{seven}& \\ +\; 3555_{seven}& \\ \hline \end{split} \nonumber \]
The Standard Algorithm for Addition
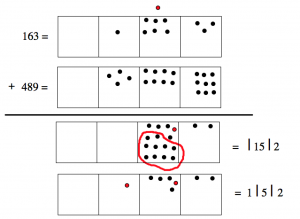
Let’s go back to the example 163+489. Some teachers don’t like writing:
\[\begin{split} 1\; \; \; 6\; \; \; 3& \\ +\; 4\; \; \; 8\; \; \; 9& \\ \hline 5 | 14 | 12& = 652 \end{split} \nonumber \]
They prefer to teach their students to start with the 3 and 9 at the end and sum those to get 12. This is of course correct — we got 12 as well.

But they don’t want students to write or think “twelvety,” so they have their students write something like this:
\[\begin{split} 1& \\ 16&3 \\ +\; 48&9 \\ \hline &2 \end{split} \nonumber \]
This can seem completely mysterious. What’s really going on? They are exploding ten dots, of course!
Now we carry on with the problem and add the tens. Students are taught to write:
\[\begin{split} 1& \\ 1&63 \\ +\; 4&89 \\ \hline &52 \end{split} \nonumber \]
But what this means is better shown in this next picture. Notice the “exploded” (or regrouped) dot at the very top, which is added to the tens box in the answer.
And now we finish the problem by combining the dots in the hundreds boxes:
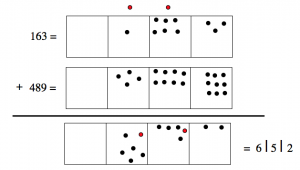
\[\begin{split} 1& \\ 1&63 \\ +\; 4&89 \\ \hline 6&52 \end{split} \nonumber \]
In the standard algorithm, we work from right to left, doing the “explosions” as we go along. This means that we start adding at the ones place and work towards the left-most place value, “carrying” digits that come from the explosions. (This is really not carrying; a better term for it is regrouping. Ten ones become one ten. Ten tens become one hundred. And so on.)
In the dots and boxes method, we add in any direction or order we like and then we do the explosions at the end.
- Why do we like the standard algorithm? Because it is efficient.
- Why do we like the dots and boxes method? Because it is easy to understand.











