7.E: Trigonometric Identities and Equations (Exercises)
- Last updated
- Save as PDF
- Page ID
- 13499
7.1: Solving Trigonometric Equations with Identities
In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.
Verbal
1) We know \(g(x)=\cos x\) is an even function, and \(f(x)=\sin x\) and \(h(x)=\tan x\)are odd functions. What about \(G(x)=\cos ^2 x\), \(F(x)=\sin ^2 x\) and \(H(x)=\tan ^2 x\)? Are they even, odd, or neither? Why?
- Answer
-
All three functions, \(F,G,\) and \(H\)
, This is because
\(F(-x)=\sin(-x)\sin(-x)=(-\sin x)(-\sin x)=\sin^2 x=F(x),G(-x)=\cos(-x)\cos(-x)=\cos x\cos x= cos^2 x=H(-x)=\tan(-x)\tan(-x)=(-\tan x)(-\tan x)=\tan2x=H(x)\)
2) Examine the graph of \(f(x)=\sec x\) on the interval \([-\pi ,\pi ]\)
3) After examining the reciprocal identity for \(\sec t\)
- Answer
-
When \(\cos t = 0\)
, ,
4) All of the Pythagorean identities are related. Describe how to manipulate the equations to get from \(\sin^2t+\cos^2t=1\) to the other forms.
Algebraic
For the exercises 5-15, use the fundamental identities to fully simplify the expression.
5) \(\sin x \cos x \sec x\)
- Answer
-
\(\sin x\)
6) \(\sin(-x)\cos(-x)\csc(-x)\)
7) \(\tan x\sin x+\sec x\cos^2x\)
- Answer
-
\(\sec x\)
8) \(\csc x+\cos x\cot(-x)\)
9) \(\dfrac{\cot t+\tan t}{\sec (-t)}\)
- Answer
-
\(\csc x\)
10) \(3\sin^3 t\csc t+\cos^2 t+2\cos(-t)\cos t\)
11) \(-\tan(-x)\cot(-x)\)
- Answer
-
\(-1\)
12) \(\dfrac{-\sin (-x)\cos x\sec x\csc x\tan x}{\cot x}\)
13) \(\dfrac{1+\tan ^2\theta }{\csc ^2\theta }+\sin ^2\theta +\dfrac{1}{\sec ^2 \theta }\)
- Answer
-
\(\sec^2 x\)
14) \(\left (\dfrac{\tan x}{\csc ^2 x}+\dfrac{\tan x}{\sec ^2 x} \right )\left (\dfrac{1+\tan x}{1+\cot x} \right )-\dfrac{1}{\cos ^2 x}\)
15) \(\dfrac{1-\cos ^2 x}{\tan ^2 x}+2\sin ^2 x\)
- Answer
-
\(\sin^2 x+1\)
For the exercises 16-28, simplify the first trigonometric expression by writing the simplified form in terms of the second expression.
16) \(\dfrac{\tan x+\cot x}{\csc x}; \cos x\)
17) \(\dfrac{\sec x+\csc x}{1+\tan x}; \sin x\)
- Answer
-
\(\dfrac{1}{\sin x}\)
18) \(\dfrac{\cos x}{1+\sin x}+\tan x; \cos x\)
19) \(\dfrac{1}{\sin x\cos x}-\cot x; \cot x\)
- Answer
-
\(\dfrac{1}{\cot x}\)
20) \(\dfrac{1}{1-\cos x}-\dfrac{\cos x}{1+\cos x}; \csc x\)
21) \((\sec x+\csc x)(\sin x+\cos x)-2-\cot x; \tan x\)
- Answer
-
\(\tan x\)
22) \(\dfrac{1}{\csc x-\sin x}; \sec x\) and \(\tan x\)
23) \(\dfrac{1-\sin x}{1+\sin x}-\dfrac{1+\sin x}{1-\sin x}; \sec x\) and \(\tan x\)
- Answer
-
\(-4\sec x \tan x\)
24) \(\tan x; \sec x\)
25) \(\sec x; \cot x\)
- Answer
-
\(\pm \sqrt{\dfrac{1}{\cot ^2 x}+1}\)
26) \(\sec x; \sin x\)
27) \(\cot x; \sin x\)
- Answer
-
\(\dfrac{\pm \sqrt{1-\sin ^2 x}}{\sin x}\)
28) \(\cot x; \csc x\)
For the exercises 29-33, verify the identity.
29) \(\cos x-\cos^3x=\cos x \sin^2 x\)
- Answer
-
Answers will vary. Sample proof:
\(\begin{align*} \cos x-\cos^3x &= \cos x (1-\cos^2 x)\\ &= \cos x\sin ^x \end{align*}\)
30) \(\cos x(\tan x-\sec(-x))=\sin x-1\)
31) \(\dfrac{1+\sin ^2x}{\cos ^2 x}=\dfrac{1}{\cos ^2 x}+\dfrac{\sin ^2x}{\cos ^2 x}=1+2\tan ^2x\)
- Answer
-
Answers will vary. Sample proof:
\(\begin{align*} \dfrac{1+\sin ^2x}{\cos ^2 x} &= \dfrac{1}{\cos ^2 x}+\dfrac{\sin ^2x}{\cos ^2 x}\\ &= \sec ^2x+\tan ^2x\\ &= \tan ^2x+1+\tan ^2x\\ &= 1+2\tan ^2x \end{align*}\)
32) \((\sin x+\cos x)^2=1+2 \sin x\cos x\)
33) \(\cos^2x-\tan^2x=2-\sin^2x-\sec^2x\)
- Answer
-
Answers will vary. Sample proof:
\(\begin{align*} \cos^2x-\tan^2x &= 1-\sin^2x-\left (\sec^2x -1 \right )\\ &= 1-\sin^2x-\sec^2x +1\\ &= 2-\sin^2x-\sec^2x \end{align*}\)
Extensions
For the exercises 34-39, prove or disprove the identity.
34) \(\dfrac{1}{1+\cos x}-\dfrac{1}{1-\cos (-x)}=-2\cot x\csc x\)
35) \(\csc^2x(1+\sin^2x)=\cot^2x\)
- Answer
-
False
36) \(\left (\dfrac{\sec ^2(-x)-\tan ^2x}{\tan x} \right )\left (\dfrac{2+2\tan x}{2+2\cot x} \right )-2\sin ^2 x=\cos (2x) \)
37) \(\dfrac{\tan x}{\sec x}\sin (-x)=\cos ^2x\)
- Answer
-
False
38) \(\dfrac{\sec (-x)}{\tan x+\cot x}=-\sin (-x)\)
39) \(\dfrac{1+\sin x}{\cos x}=\dfrac{\cos x}{1+\sin (-x)}\)
- Answer
-
Proved with negative and Pythagorean identities
For the exercises 40-, determine whether the identity is true or false. If false, find an appropriate equivalent expression.
40) \(\dfrac{\cos ^2 \theta -\sin ^2 \theta }{1-\tan ^2 \theta }=\sin ^2 \theta\)
41) \(3\sin^2\theta + 4\cos^2\theta =3+\cos^2\theta\)
- Answer
-
True
\(\begin{align*} 3\sin^2\theta + 4\cos^2\theta &= 3\sin ^2\theta +3\cos ^2\theta +\cos^2\theta \\ &= 3\left ( \sin ^2\theta +\cos ^2\theta \right )+\cos^2\theta \\ &= 3+\cos^2\theta \end{align*}\)
42) \(\dfrac{\sec \theta +\tan \theta }{\cot \theta+\cos ^\theta }=\sec ^2 \theta\)
7.2: Sum and Difference Identities
In this section, we will learn techniques that will enable us to solve useful problems. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.
Verbal
1) Explain the basis for the cofunction identities and when they apply.
- Answer
-
The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures \(x\)
, . .
2) Is there only one way to evaluate \(\cos \left (\dfrac{5\pi }{4} \right )\)
3) Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas can determine this characteristic for \(f(x)=\sin (x)\) and \(g(x)=\cos (x)\)
- Answer
-
\(\sin (-x)=-\sin x\), so \(\sin x\) is odd. \(\cos (-x)=\cos (0-x)=\cos x\), so \(\cos x\) is even.
Algebraic
For the exercises 4-9, find the exact value.
4) \(\cos \left (\dfrac{7\pi }{12} \right)\)
5) \(\cos \left (\dfrac{\pi }{12} \right)\)
- Answer
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
6) \(\sin \left (\dfrac{5\pi }{12} \right)\)
7) \(\sin \left (\dfrac{11\pi }{12} \right)\)
- Answer
-
\(\dfrac{\sqrt{6}-\sqrt{2}}{4}\)
8) \(\tan \left (-\dfrac{\pi }{12} \right)\)
9) \(\tan \left (\dfrac{19\pi }{12} \right)\)
- Answer
-
\(-2-\sqrt{3}\)
For the exercises 10-13, rewrite in terms of \(\sin x\) and \(\cos x\)
10) \(\sin \left (x+\dfrac{11\pi }{6} \right)\)
11) \(\sin \left (x-\dfrac{3\pi }{4} \right)\)
- Answer
-
\(-\dfrac{\sqrt{2}}{2}\sin x-\dfrac{\sqrt{2}}{2}\cos x\)
12) \(\cos \left (x-\dfrac{5\pi }{6} \right)\)
13) \(\cos \left (x+\dfrac{2\pi }{3} \right)\)
- Answer
-
\(-\dfrac{1}{2}\cos x-\dfrac{\sqrt{3}}{2}\sin x\)
For the exercises 14-19, simplify the given expression.
14) \(\csc \left (\dfrac{\pi }{2}-t \right)\)
15) \(\sec \left (\dfrac{\pi }{2}-\theta \right)\)
- Answer
-
\(\csc \theta\)
16) \(\cot \left (\dfrac{\pi }{2}-x \right)\)
17) \(\tan \left (\dfrac{\pi }{2}-x \right)\)
- Answer
-
\(\cot x\)
18) \(\sin(2x)\cos(5x)-\sin(5x)\cos(2x)\)
19) \(\dfrac{\tan \left (\dfrac{3}{2}x \right)-\tan \left (\dfrac{7}{5}x \right)}{1+\tan \left (\dfrac{3}{2}x \right)\tan \left (\dfrac{7}{5}x \right)}\)
- Answer
-
\(\tan \left (\dfrac{x}{10} \right)\)
For the exercises 20-21, find the requested information.
20) Given that \(\sin a=\dfrac{2}{3}\) and \(\cos b=-\dfrac{1}{4}\)
21) Given that \(\sin a=\dfrac{4}{5}\) and \(\cos b=\dfrac{1}{3}\), with \(a\) and \(b\) both in the interval \(\left [ 0, \dfrac{\pi }{2} \right )\), find \(\sin (a-b)\) and \(\cos (a+b)\).
- Answer
-
\(\sin (a-b)=\left ( \dfrac{4}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{3}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{4-6\sqrt{2}}{15}\)
\(\cos (a+b)=\left ( \dfrac{3}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{4}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{3-8\sqrt{2}}{15}\)
For the exercises 22-24, find the exact value of each expression.
22) \(\sin \left ( \cos^{-1}\left ( 0 \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )\)
23) \(\cos \left ( \cos^{-1}\left ( \dfrac{\sqrt{2}}{2} \right )+ \sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )\right )\)
- Answer
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
24) \(\tan \left ( \sin^{-1}\left ( \dfrac{1}{2} \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )\)
Graphical
For the exercises 25-32, simplify the expression, and then graph both expressions as functions to verify the graphs are identical.
25) \(\cos \left ( \dfrac{\pi }{2}-x \right )\)
- Answer
-
\(\sin x\)
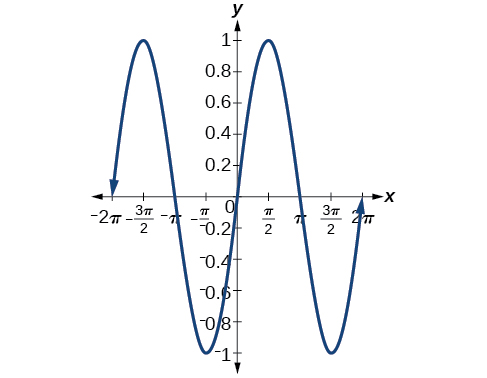
26) \(\sin (\pi -x)\)
27) \(\tan \left ( \dfrac{\pi }{3}+x \right )\)
- Answer
-
\(\cot \left ( \dfrac{\pi }{6}-x \right )\)
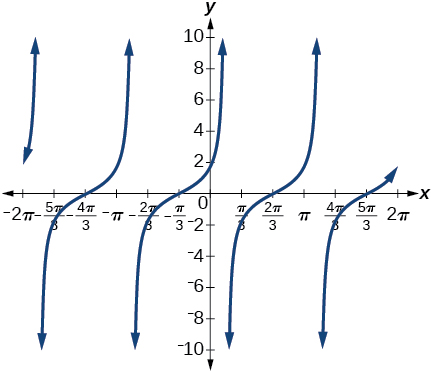
28) \(\sin \left ( \dfrac{\pi }{3}+x \right )\)
29) \(\tan \left ( \dfrac{\pi }{4}-x \right )\)
- Answer
-
\(\cot \left ( \dfrac{\pi }{4}+x \right )\)
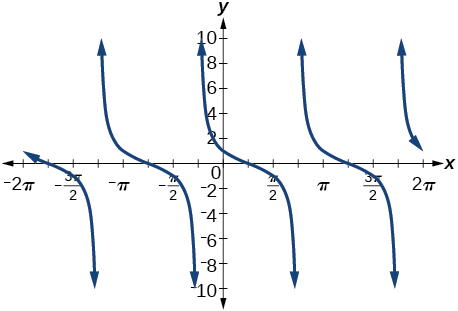
30) \(\cos \left ( \dfrac{7\pi }{6}+x \right )\)
31) \(\sin \left ( \dfrac{\pi }{4}+x \right )\)
- Answer
-
\(\dfrac{\sin x}{\sqrt{2}}+\dfrac{\cos x}{\sqrt{2}}\)
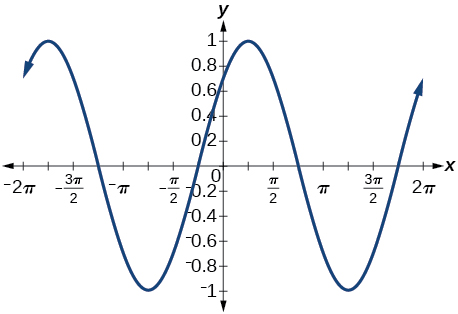
32) \(\cos \left ( \dfrac{5\pi }{4}+x \right )\)
For the exercises 33-41, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are different, replace the second function with one that is identical to the first. (Hint: think \(2x=x+x\))
33) \(f(x)=\sin(4x)-\sin(3x)\cos x, g(x)=\sin x \cos(3x)\)
- Answer
-
They are the same.
34) \(f(x)=\cos(4x)+\sin x \sin(3x), g(x)=-\cos x \cos(3x)\)
35) \(f(x)=\sin(3x)\cos(6x), g(x)=-\sin(3x)\cos(6x)\)
- Answer
-
They are different, try \(g(x)=\sin(9x)-\cos(3x)\sin(6x)\)
36) \(f(x)=\sin(4x), g(x)=\sin(5x)\cos x-\cos(5x)\sin x\)
37) \(f(x)=\sin(2x), g(x)=2 \sin x \cos x\)
- Answer
-
They are the same.
38) \(f(\theta )=\cos(2\theta ), g(\theta )=\cos^2\theta -\sin^2\theta\)
39) \(f(\theta )=\tan(2\theta ), g(\theta )=\dfrac{\tan \theta }{1+\tan^2\theta }\)
- Answer
-
They are different, try \(g(\theta )=\dfrac{2\tan \theta }{1-\tan^2\theta }\)
40) \(f(x)=\sin(3x)\sin x, g(x)=\sin^2(2x)\cos^2x-\cos^2(2x)\sin2x\)
41) \(f(x)=\tan(-x), g(x)=\dfrac{\tan x-\tan(2x)}{1-\tan x \tan(2x)}\)
- Answer
-
They are different, try \(g(x)=\dfrac{\tan x-\tan(2x)}{1+\tan x \tan(2x)}\)
Technology
For the exercises 42-46, find the exact value algebraically, and then confirm the answer with a calculator to the fourth decimal point.
42) \(\sin (75^{\circ})\)
43) \(\sin (195^{\circ})\)
- Answer
-
\(-\dfrac{\sqrt{3}-1}{2\sqrt{2}}\), or \(-0.2588\)
44) \(\cos (165^{\circ})\)
45) \(\cos (345^{\circ})\)
- Answer
-
\(\dfrac{1+\sqrt{3}}{2\sqrt{2}}\), or \(-0.9659\)
46) \(\tan (-15^{\circ})\)
Extensions
For the exercises 47-51, prove the identities provided.
47) \(\tan \left ( x+\dfrac{\pi }{4} \right )=\dfrac{\tan x+1}{1-\tan x}\)
- Answer
-
\(\begin{align*} \tan \left ( x+\dfrac{\pi }{4} \right ) &= \\ \dfrac{\tan x + \tan\left (\tfrac{\pi}{4} \right )}{1-\tan x \tan\left (\tfrac{\pi}{4} \right )} &= \\ \dfrac{\tan x+1}{1-\tan x(1)} &= \dfrac{\tan x+1}{1-\tan x} \end{align*}\)
48) \(\dfrac{\tan (a+b)}{\tan (a-b)}=\dfrac{\sin a \cos a + \sin b \cos b}{\sin a \cos a - \sin b \cos b}\)
49) \(\dfrac{\cos (a+b)}{\cos a \cos b}=1-\tan a \tan b\)
- Answer
-
\(\begin{align*} \dfrac{\cos (a+b)}{\cos a \cos b} &= \\ \dfrac{\cos a \cos b}{\cos a \cos b}- \dfrac{\sin a \sin b}{\cos a \cos b} &= 1-\tan a \tan b \end{align*}\)
50) \(\cos(x+y)\cos(x-y)=\cos^2x-\sin^2y\)
51) \(\dfrac{\cos(x+h)-\cos(x)}{h}=\cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h}\)
- Answer
-
\(\begin{align*} \dfrac{\cos(x+h)-\cos(x)}{h} &= \\ \dfrac{\cos x\cosh - \sin x\sinh -\cos x}{h} &= \\ \dfrac{\cos x(\cosh-1) - \sin x(\sinh-1)}{h} &= \cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h} \end{align*}\)
For the exercises 52-, prove or disprove the statements.
52) \(\tan (u+v)=\dfrac{\tan u+\tan v}{1-\tan u \tan v}\)
53) \(\tan (u-v)=\dfrac{\tan u-\tan v}{1+\tan u \tan v}\)
- Answer
-
True
54) \(\dfrac{\tan (x+y)}{1+\tan x \tan x}=\dfrac{\tan x + \tan y}{1-\tan^2 x \tan^2 y}\)
55) If \(\alpha ,\beta\)
- Answer
-
True. Note that \(\sin (\alpha +\beta )=\sin (\pi -\gamma )\) and expand the right hand side.
56) If \(\alpha ,\beta\), and \(\gamma\) are angles in the same triangle, then prove or disprove \(\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma\).
7.3: Double-Angle, Half-Angle, and Reduction Formulas
In this section, we will investigate three additional categories of identities. Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent. Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term. Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not.
Verbal
1) Explain how to determine the reduction identities from the double-angle identity \(\cos(2x)=\cos^2x-\sin^2x\)
- Answer
-
Use the Pythagorean identities and isolate the squared term.
2) Explain how to determine the double-angle formula for \(\tan(2x)\) using the double-angle formulas for \(\cos(2x)\) and \(\sin (2x)\).
3) We can determine the half-angle formula for \(\tan \left ( \dfrac{x}{2} \right )=\dfrac{\sqrt{1-\cos x}}{\sqrt{1+\cos x}}\) by dividing the formula for \(\sin \left ( \dfrac{x}{2} \right )\) by \(\cos \left ( \dfrac{x}{2} \right )\). Explain how to determine two formulas for \(\tan \left ( \dfrac{x}{2} \right )\) that do not involve any square roots.
- Answer
-
\(\dfrac{1-\cos x}{\sin x}\), \(\dfrac{\sin x}{1+\cos x}\), multiplying the top and bottom by \(\sqrt{1-\cos x}\) and \(\sqrt{1+\cos x}\), respectively.
4) For the half-angle formula given in the previous exercise for \(\tan \left ( \dfrac{x}{2} \right )\)
Algebraic
For the exercises 5-8, find the exact values of a) \(\sin (2x)\), b) \(\cos(2x)\)
5) If \(\sin x =\dfrac{1}{8}\)
- Answer
-
- \(\dfrac{3\sqrt{7}}{32}\)
- \(\dfrac{31}{32}\)
- \(\dfrac{3\sqrt{7}}{31}\)
6) If \(\cos x =\dfrac{2}{3}\), and \(x\) is in quadrant \(\mathrm{I}\).
7) If \(\cos x =-\dfrac{1}{2}\), and \(x\) is in quadrant \(\mathrm{III}\).
- Answer
-
- \(\dfrac{\sqrt{3}}{2}\)
- \(-\dfrac{1}{2}\)
- \(-\sqrt{3}\)
8) If \(\tan x =-8\), and \(x\) is in quadrant \(\mathrm{IV}\).
For the exercises 9-10, find the values of the six trigonometric functions if the conditions provided hold.
9) \(\cos(2\theta )=\dfrac{3}{5}\) and \(90^{\circ}\leq \theta \leq 180^{\circ}\)
- Answer
-
\(\cos \theta =-\frac{2\sqrt{5}}{5},\sin \theta =\frac{\sqrt{5}}{5},\tan \theta =-\frac{1}{2},\csc \theta =\sqrt{5},\sec \theta =-\frac{\sqrt{5}}{2},\cot \theta =-2\)
10) \(\cos(2\theta )=\dfrac{1}{\sqrt{2}}\) and \(180^{\circ}\leq \theta \leq 270^{\circ}\)
For the exercises 11-12, simplify to one trigonometric expression.
11) \(2\sin \left ( \dfrac{\pi }{4} \right )2\cos \left ( \dfrac{\pi }{4} \right )\)
- Answer
-
\(2\sin \left ( \dfrac{\pi }{2} \right )\)
12) \(4\sin \left ( \dfrac{\pi }{8} \right )\cos \left ( \dfrac{\pi }{8} \right )\)
For the exercises 13-19, find the exact value using half-angle formulas.
13) \(\sin \left ( \dfrac{\pi }{8} \right )\)
- Answer
-
\(\dfrac{\sqrt{2-\sqrt{2}}}{2}\)
14) \(\cos \left ( -\dfrac{11\pi }{12} \right )\)
15) \(\sin \left ( \dfrac{11\pi }{12} \right )\)
- Answer
-
\(\dfrac{\sqrt{2-\sqrt{3}}}{2}\)
16) \(\cos \left ( \dfrac{7\pi }{8} \right )\)
17) \(\tan \left ( \dfrac{5\pi }{12} \right )\)
- Answer
-
\(2+\sqrt{3}\)
18) \(\tan \left ( -\dfrac{3\pi }{12} \right )\)
19) \(\tan \left ( -\dfrac{3\pi }{8} \right )\)
- Answer
-
\(-1-\sqrt{2}\)
For the exercises 20-23, find the exact values of a) \(\sin \left ( \dfrac{x}{2} \right )\) b) \(\cos \left ( \dfrac{x}{2} \right )\)
20) If \(\tan x =-\dfrac{4}{3}\), and \(x\) is in quadrant \(\mathrm{IV}\).
21) If \(\sin x =-\dfrac{12}{13}\), and \(x\) is in quadrant \(\mathrm{III}\).
- Answer
-
- \(\dfrac{3\sqrt{13}}{13}\)
- \(-\dfrac{2\sqrt{13}}{13}\)
- \(-\dfrac{3}{2}\)
22) If \(\csc x =7\), and \(x\) is in quadrant \(\mathrm{II}\).
23) If \(\sec x =-4\), and \(x\) is in quadrant \(\mathrm{II}\).
- Answer
-
- \(\dfrac{\sqrt{10}}{4}\)
- \(\dfrac{\sqrt{6}}{4}\)
- \(\dfrac{\sqrt{15}}{3}\)
For the exercises 24-27, use Figure below to find the requested half and double angles.
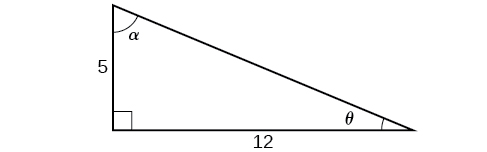
24) Find \(\sin (2\theta )\), \(\cos (2\theta )\)
25) Find \(\sin (2\alpha )\), \(\cos (2\alpha )\), and \(\tan (2\alpha )\).
- Answer
-
\(\dfrac{120}{169}, -\dfrac{119}{169}, -\dfrac{120}{119}\)
26) Find \(\sin \left (\dfrac{\theta }{2} \right )\), \(\cos \left (\dfrac{\theta }{2} \right )\), and \(\tan \left (\dfrac{\theta }{2} \right )\).
27) Find \(\sin \left (\dfrac{\alpha }{2} \right )\), \(\cos \left (\dfrac{\alpha }{2} \right )\), and \(\tan \left (\dfrac{\alpha }{2} \right )\).
- Answer
-
\(\dfrac{2\sqrt{13}}{13}, \dfrac{3\sqrt{13}}{13}, \dfrac{2}{3}\)
For the exercises 28-33, simplify each expression. Do not evaluate.
28) \(\cos ^2(28^{\circ})-\sin ^2(28^{\circ})\)
29) \(2\cos ^2(37^{\circ})-1\)
- Answer
-
\(\cos (74^{\circ})\)
30) \(1-2\sin ^2(17^{\circ})\)
31) \(\cos ^2(9x)-\sin ^2(9x)\)
- Answer
-
\(\cos (18x)\)
32) \(4\sin (8x)\cos (8x)\)
33) \(6\sin (5x)\cos (5x)\)
- Answer
-
\(3\sin (10x)\)
For the exercises 34-37, prove the identity given.
34) \((\sin t-\cos t)^2=1-\sin(2t)\)
35) \(\sin(2x)=-2 \sin(-x) \cos(-x)\)
- Answer
-
\(-2 \sin(-x)\cos(-x)=-2(-\sin(x)\cos(x))=\sin(2x)\)
36) \(\cot x-\tan x=2 \cot(2x)\)
37) \(\dfrac{1+\cos (2\theta )}{\sin (2\theta )}\tan ^2\theta =\tan \theta\)
- Answer
-
\(\dfrac{\sin (2\theta )}{1+\cos (2\theta )}\tan ^2\theta =\dfrac{2\sin (\theta )\cos (\theta )}{1+\cos ^2\theta -\sin ^2\theta }\tan ^2\theta=\)
\(\dfrac{2\sin (\theta )\cos (\theta )}{2\cos ^2\theta }\tan ^2\theta=\dfrac{\sin (\theta )}{\cos (\theta )}\tan ^2\theta=\)
\(\cot (\theta )\tan ^2\theta=\tan \theta\)
For the exercises 38-44, rewrite the expression with an exponent no higher than 1.
38) \(\cos ^2 (5x)\)
39) \(\cos ^2 (6x)\)
- Answer
-
\(\dfrac{1+\cos (12x)}{2}\)
40) \(\sin ^4 (8x)\)
41) \(\sin ^4 (3x)\)
- Answer
-
\(\dfrac{3+\cos(12x)-4\cos(6x)}{8}\)
42) \(\cos^2x \sin^4x\)
43) \(\cos^4x \sin^2x\)
- Answer
-
\(\dfrac{2+\cos(2x)-2\cos(4x)-\cos(6x)}{32}\)
44) \(\tan^2x \sin^2x\)
Technology
For the exercises 45-52, reduce the equations to powers of one, and then check the answer graphically.
45) \(\tan^4x\)
- Answer
-
\(\dfrac{3+\cos(4x)-4\cos(2x)}{3+\cos(4x)+4\cos(2x)}\)
46) \(\sin^2(2x)\)
47) \(\sin^2x \cos^2x\)
- Answer
-
\(\dfrac{1-\cos(4x)}{8}\)
48) \(\tan^2x \sin x\)
49) \(\tan^4x \cos^2 x\)
- Answer
-
\(\dfrac{3+\cos(4x)-4\cos(2x)}{4(\cos(2x)+1)}\)
50) \(\cos^2x \sin (2x)\)
51) \(\cos^2(2x) \sin x\)
- Answer
-
\(\dfrac{(1+\cos(4x))\sin x}{2}\)
52) \(\tan ^2\left ( \dfrac{x}{2} \right )\sin x\)
For the exercises 53-54, algebraically find an equivalent function, only in terms of \(\sin x\) and/or \(\cos x\)
53) \(\sin (4x)\)
- Answer
-
\(4\sin x\cos x(\cos^2x-\sin^2x)\)
54) \(\cos (4x)\)
Extensions
For the exercises 55-63, prove the identities.
55) \(\sin (2x)=\dfrac{2\tan x}{1+\tan ^2x}\)
- Answer
-
\(\dfrac{2\tan x}{1+\tan ^2x}=\dfrac{\tfrac{2\sin x}{\cos x}}{1+\tfrac{\sin ^2x}{\cos ^2x}}=\dfrac{\tfrac{2\sin x}{\cos x}}{\tfrac{\cos ^2x+\sin ^2x}{\cos ^2x}}=\dfrac{2\sin x}{\cos x}\cdot \dfrac{\cos ^2x}{1}=2\sin x \cos x=\sin (2x)\)
56) \(\cos (2\alpha )=\dfrac{1-\tan ^2\alpha }{1+\tan ^2\alpha }\)
57) \(\tan (2x)=\dfrac{2\sin x \cos x }{2\cos ^2 x-1}\)
- Answer
-
\(\dfrac{2\sin x \cos x }{2\cos ^2 x-1}=\dfrac{\sin (2x)}{ \cos (2x)}=\tan (2x)\)
58) \((\sin^2x-1)^2=\cos(2x)+\sin^4x\)
59) \(\sin(3x)=3\sin x \cos^2x-\sin^3x\)
- Answer
-
\(\begin{align*} \sin (x+2x) &= \sin x \cos (2x)+\sin (2x) \cos x\\ &= \sin x(\cos ^2 x - \sin ^2 x)+2\sin x \cos x \cos x\\ &= \sin x \cos ^2 x-\sin ^3 x + 2\sin x\cos ^2 x\\ &= 3\sin x\cos ^2 x - \sin ^3 x \end{align*}\)
60) \(\cos(3x)=\cos^3x-3\sin^2x\cos x\)
61) \(\dfrac{1+\cos (2t)}{\sin (2t)-\cos t}=\dfrac{2\cos t}{2\sin t-1}\)
- Answer
-
\(\begin{align*} \dfrac{1+\cos (2t)}{\sin (2t)-\cos t} &= \dfrac{1+2\cos ^2t-1}{2\sin t\cos t-\cos t}\\ &= \dfrac{2\cos ^2t}{\cos t(2\sin t-1)}\\ &= \dfrac{2\cos t}{2\sin t-1} \end{align*}\)
62) \(\sin(16x)=16 \sin x \cos x \cos(2x)\cos(4x)\cos(8x)\)
63) \(\cos(16x)=(\cos^2(4x)-\sin^2(4x)-\sin(8x))(\cos^2(4x)-\sin^2(4x)+\sin(8x))\)
- Answer
-
\(\begin{align*} (\cos^2(4x)-\sin^2(4x)-\sin(8x))(\cos^2(4x)-\sin^2(4x)+\sin(8x)) &= (\cos(8x)-\sin(8x))(\cos(8x)+\sin(8x))\\ &= \cos ^2 (8x)-\sin ^2 (8x)\\ &= \cos(16x) \end{align*}\)
7.4: Sum-to-Product and Product-to-Sum Formulas
From the sum and difference identities, we can derive the product-to-sum formulas and the sum-to-product formulas for sine and cosine. The product-to-sum formulas can rewrite products of sines, products of cosines, and products of sine and cosine as sums or differences of sines and cosines. We can also derive the sum-to-product identities from the product-to-sum identities using substitution. The sum-to-product formulas are used to rewrite sum or difference as products of sines and cosines.
Verbal
1) Starting with the product to sum formula \(\sin \alpha \cos \beta =\dfrac{1}{2} \left[\sin(\alpha +\beta )+\sin(\alpha -\beta ) \right]\)
- Answer
-
Substitute \(\alpha \) into cosine and \(\beta \) into sine and evaluate.
2) Explain two different methods of calculating \(\cos (195^{\circ}) \cos (105^{\circ})\)
3) Explain a situation where we would convert an equation from a sum to a product and give an example.
- Answer
-
Answers will vary. There are some equations that involve a sum of two trig expressions where when converted to a product are easier to solve. For example: \(\dfrac{\sin (3x)+\sin x}{\cos x}=1\)
.
4) Explain a situation where we would convert an equation from a product to a sum, and give an example.
Algebraic
For the exercises 5-10, rewrite the product as a sum or difference.
5) \(16\sin(16x)\sin(11x)\)
- Answer
-
\(8(\cos(5x)-\cos(27x))\)
6) \(2\cos(36t)\cos(6t)\)
7) \(2\sin(5x)\cos(3x)\)
- Answer
-
\(\sin(2x)+\sin(8x)\)
8) \(10\cos(5x)\sin(10x)\)
9) \(\sin(-x)\sin(5x)\)
- Answer
-
\(\dfrac{1}{2}(\cos(6x)-\cos(4x))\)
10) \(\sin(3x)\cos(5x)\)
For the exercises 11-16, rewrite the sum or difference as a product.
11) \(\cos(6t)+\cos(4t)\)
- Answer
-
\(2\cos(5t)\cos t\)
12) \(\sin(3x)+\sin(7x)\)
13) \(\cos(7x)+\cos(-7x)\)
- Answer
-
\(2\cos(7x)\)
14) \(\sin(3x)-\sin(-3x)\)
15) \(\cos(3x)+\cos(9x)\)
- Answer
-
\(2\cos(6x)\cos(3x)\)
16) \(\sin h-\sin(3h)\)
For the exercises 17-21, evaluate the product for the following using a sum or difference of two functions.
17) \(\cos (45^{\circ}) \cos (15^{\circ})\)
- Answer
-
\(\dfrac{1}{4}(1+\sqrt{3})\)
18) \(\cos (45^{\circ}) \sin (15^{\circ})\)
19) \(\sin (-345^{\circ}) \sin (-15^{\circ})\)
- Answer
-
\(\dfrac{1}{4}(\sqrt{3}-2)\)
20) \(\sin (195^{\circ}) \cos (15^{\circ})\)
21) \(\sin (-45^{\circ}) \sin (-15^{\circ})\)
- Answer
-
\(\dfrac{1}{4}(\sqrt{3}-1)\)
For the exercises 22-26, evaluate the product using a sum or difference of two functions. Leave in terms of sine and cosine.
22) \(\cos (23^{\circ}) \sin (17^{\circ})\)
23) \(2\sin (100^{\circ}) \sin (20^{\circ})\)
- Answer
-
\(\cos (80^{\circ})-\cos (120^{\circ})\)
24) \(2\sin (-100^{\circ})\sin (-20^{\circ})\)
25) \(\sin (213^{\circ})\cos (8^{\circ})\)
- Answer
-
\(\dfrac{1}{2}\left (\sin (221^{\circ})+\sin (205^{\circ}) \right )\)
26) \(2\cos (56^{\circ})\cos (47^{\circ})\)
For the exercises 27-31, rewrite the sum as a product of two functions. Leave in terms of sine and cosine.
27) \(\sin (76^{\circ})+\sin (14^{\circ})\)
- Answer
-
\(\sqrt{3}\cos (31^{\circ})\)
28) \(\cos (58^{\circ})-\cos (12^{\circ})\)
29) \(\sin (101^{\circ})-\sin (32^{\circ})\)
- Answer
-
\(2\cos (66.5^{\circ})\sin (34.5^{\circ})\)
30) \(\cos (100^{\circ})+\cos (200^{\circ})\)
31) \(\sin (-1^{\circ})+\sin (-2^{\circ})\)
- Answer
-
\(2\sin (-1.5^{\circ})\cos (0.5^{\circ})\)
For the exercises 32-38, prove the identity.
32) \(\dfrac{\cos (a-b)}{\cos (a+b)}=\dfrac{1-\tan a \tan b}{1+\tan a \tan b}\)
33) \(4\sin(3x)\cos(4x)=2\sin(7x)-2\sin x\)
- Answer
-
\(\begin{align*} 2\sin(7x)-2\sin x &= 2\sin(4x+3x)-2\sin(4x-3x)\\ &= 2(\sin(4x)\cos(3x)+\sin(3x)\cos(4x))-2(\sin(4x)\cos(3x)-\sin(3x)\cos(4x))\\ &= 2\sin(4x)\cos(3x)+2\sin(3x)\cos(4x))-2\sin(4x)\cos(3x)+2\sin(3x)\cos(4x))\\ &= 4\sin(3x)\cos(4x) \end{align*}\)
34) \(\dfrac{6\cos (8x)\sin (2x)}{\sin (-6x)}=-3\sin(10x)\csc(6x)+3\)
35) \(\sin x + \sin(3x)=4\sin x\cos^2 x\)
- Answer
-
\(\begin{align*} \sin x + \sin(3x) &= 2\sin\left ( \dfrac{4x}{2} \right )\cos\left ( -\dfrac{2x}{2} \right )\\ &= 2\sin(2x)\cos x\\ &= 2(2\sin x \cos x)\cos x\\ &= 4\sin x\cos^2 x \end{align*}\)
36) \(2(\cos^3x-\cos x \sin^2x)=\cos(3x)+\cos x\)
37) \(2\tan x \cos(3x)=\sec x(\sin(4x)-\sin(2x))\)
- Answer
-
\(\begin{align*} 2\tan x \cos(3x) &= \dfrac{2\sin x\cos (3x)}{\cos x}\\ &= \dfrac{2(.5(\sin (4x)-\sin (2x)))}{\cos x}\\ &= \dfrac{1}{\cos x}(\sin(4x)-\sin(2x))\\ &= \sec x(\sin(4x)-\sin(2x)) \end{align*}\)
38) \(\cos(a+b)+\cos(a-b)=2\cos a \cos b\)
Numeric
For the exercises 39-43, rewrite the sum as a product of two functions or the product as a sum of two functions. Give your answer in terms of sines and cosines. Then evaluate the final answer numerically, rounded to four decimal places.
39) \(\cos (58^{\circ})+\cos (12^{\circ})\)
- Answer
-
\(2\cos (35^{\circ})\cos (23^{\circ}),1.5081\)
40) \(\sin (2^{\circ})-\sin (3^{\circ})\)
41) \(\cos (44^{\circ})-\cos (22^{\circ})\)
- Answer
-
\(-2\sin (33^{\circ})\sin (11^{\circ}),-0.2078\)
42) \(\cos (176^{\circ})\sin (9^{\circ})\)
43) \(\sin (-14^{\circ})\sin (85^{\circ})\)
- Answer
-
\(\dfrac{1}{2}\left (\cos (99^{\circ})-\cos (71^{\circ}) \right ),-0.2410\)
Technology
For the exercises 44-48, algebraically determine whether each of the given expressions is a true identity. If it is not an identity, replace the right-hand side with an expression equivalent to the left side. Verify the results by graphing both expressions on a calculator.
44) \(2\sin(2x)\sin(3x)=\cos x-\cos(5x)\)
45) \(\dfrac{\cos(10\theta )+\cos(6\theta )}{\cos(6\theta )-\cos(10\theta )}=\cot(2\theta )\cot(\theta )\)
- Answer
-
It is an identity.
46) \(\dfrac{\sin(3x)-\sin(5x)}{\cos(3x)+\cos(5x)}=\tan x\)
47) \(2\cos(2x)\cos x+\sin(2x)\sin x=2\sin x\)
- Answer
-
It is not an identity, but \(2\cos ^3 x\) is.
48) \(\dfrac{\sin(2x)+\sin(4x)}{\sin(2x)-\sin(4x)}=-\tan (3x)\cot x\)
For the exercises 49-53, simplify the expression to one term, then graph the original function and your simplified version to verify they are identical.
49) \(\dfrac{\sin(9t)-\sin(3t)}{\cos(9t)+\cos(3t)}\)
- Answer
-
\(\tan (3t)\)
50) \(2\sin(8x)\cos(6x)-\sin(2x)\)
51) \(\dfrac{\sin(3x)-\sin(x)}{\sin x}\)
- Answer
-
\(2\cos (2x)\)
52) \(\dfrac{\cos(5x)+\cos(3x)}{\sin(5x)+\sin(3x)}\)
53) \(\sin x \cos(15x)-\cos x \sin(15x)\)
- Answer
-
\(-\sin (14x)\)
Extensions
For the exercises 54-55, prove the following sum-to-product formulas.
54) \(\sin x - \sin y = 2\sin \left ( \dfrac{x-y}{2} \right )\cos \left ( \dfrac{x+y}{2} \right )\)
55) \(\cos x + \cos y = 2\cos \left ( \dfrac{x+y}{2} \right )\cos \left ( \dfrac{x-y}{2} \right )\)
- Answer
-
Start with \(\cos x + \cos y\)
. , \(\cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos\alpha \cos\beta -\sin\alpha \sin\beta +\cos\alpha \cos\beta +\sin\alpha \sin\beta =2\cos\alpha \cos \beta\)
Since \(x=\alpha +\beta\) and \(y=\alpha -\beta\)
, \(2\cos \left ( \dfrac{x+y}{2} \right )\cos \left ( \dfrac{x-y}{2} \right )\)
For the exercises 56-63, prove the identity.
56) \(\dfrac{\sin(6x)+\sin(4x)}{\sin(6x)-\sin(4x)}=\tan (5x)\cot x\)
57) \(\dfrac{\cos(3x)+\cos x}{\cos(3x)-\cos(4x)}=-\cot (2x)\cot x\)
- Answer
-
\(\dfrac{\cos(3x)+\cos x}{\cos(3x)-\cos(4x)}=\dfrac{2\cos(2x)\cos x}{-2\sin(2x)\sin x}=-\cot (2x)\cot x\)
58) \(\dfrac{\cos(6y)+\cos(8y)}{\sin(6y)-\sin(4y)}=\cot y\cos(7y)\sec(5y)\)
59) \(\dfrac{\cos(2y)-\cos(4y)}{\sin(2y)+\sin(4y)}=\tan y\)
- Answer
-
\(\begin{align*} \dfrac{\cos(2y)-\cos(4y)}{\sin(2y)+\sin(4y)} &= \dfrac{-2\sin(3y)\sin(-y)}{2\sin(3y)\cos y}\\ &= \dfrac{2\sin(3y)\sin(y)}{2\sin(3y)\cos y}\\ &= \tan y \end{align*}\)
60) \(\dfrac{\sin(10x)-\sin(2x)}{\cos(10x)+\cos(2x)}=\tan(4x)\)
61) \(\cos x-\cos(3x)=4\sin^2x \cos x\)
- Answer
-
\(\begin{align*} \cos x-\cos(3x) &= -2\sin(2x)\sin(-x)\\ &= 2(2\sin x \cos x)\sin x\\ &= 4\sin^2x \cos x \end{align*}\)
62) \((\cos(2x)-\cos(4x))^2+(\sin(4x)+\sin(2x))^2=4\sin^2(3x)\)
63) \(\tan \left ( \dfrac{\pi }{4}-t \right )=\dfrac{1-\tan t}{1+\tan t}\)
- Answer
-
\(\tan \left ( \dfrac{\pi }{4}-t \right )=\dfrac{\tan \left ( \dfrac{\pi }{4} \right )-\tan t}{1+\tan \left ( \dfrac{\pi }{4} \right )\tan t}=\dfrac{1-\tan t}{1+\tan t}\)
7.5: Solving Trigonometric Equations
In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.
Verbal
1) Will there always be solutions to trigonometric function equations? If not, describe an equation that would not have a solution. Explain why or why not.
- Answer
-
There will not always be solutions to trigonometric function equations. For a basic example, \(\cos(x)=-5\).
2) When solving a trigonometric equation involving more than one trig function, do we always want to try to rewrite the equation so it is expressed in terms of one trigonometric function? Why or why not?
3) When solving linear trig equations in terms of only sine or cosine, how do we know whether there will be solutions?
- Answer
-
If the sine or cosine function has a coefficient of one, isolate the term on one side of the equals sign. If the number it is set equal to has an absolute value less than or equal to one, the equation has solutions, otherwise it does not. If the sine or cosine does not have a coefficient equal to one, still isolate the term but then divide both sides of the equation by the leading coefficient. Then, if the number it is set equal to has an absolute value greater than one, the equation has no solution.
Algebraic
For the exercises 4-12, find all solutions exactly on the interval \(0\leq \theta < 2\pi\)
4) \(2\sin \theta=-\sqrt{2}\)
5) \(2\sin \theta=\sqrt{3}\)
- Answer
-
\(\dfrac{\pi }{3}, \dfrac{2\pi }{3}\)
6) \(2\cos \theta=1\)
7) \(2\cos \theta=-\sqrt{2}\)
- Answer
-
\(\dfrac{3\pi }{4}, \dfrac{5\pi }{4}\)
8) \(\tan \theta=-1\)
9) \(\tan x=1\)
- Answer
-
\(\dfrac{\pi }{4}, \dfrac{5\pi }{4}\)
10) \(\cot x+1=0\)
11) \(4\sin^2 x-2=0\)
- Answer
-
\(\dfrac{\pi }{4}, \dfrac{3\pi }{4}, \dfrac{5\pi }{4}, \dfrac{7\pi }{4}\)
12) \(\csc^2 x-4=0\)
For the exercises 13-22, solve exactly on \([0,2\pi )\)
13) \(2\cos \theta=\sqrt{2}\)
- Answer
-
\(\dfrac{\pi }{4}, \dfrac{7\pi }{4}\)
14) \(2\cos \theta=-1\)
15) \(2\sin \theta=-1\)
- Answer
-
\(\dfrac{7\pi }{6}, \dfrac{11\pi }{6}\)
16) \(2\sin \theta=-\sqrt{3}\)
17) \(2\sin (3\theta )=1\)
- Answer
-
\(\dfrac{\pi }{18}, \dfrac{5\pi }{18}, \dfrac{13\pi }{18}, \dfrac{17\pi }{18}, \dfrac{25\pi }{18}, \dfrac{29\pi }{18}\)
18) \(2\sin (2\theta )=\sqrt{3}\)
19) \(2\cos (3\theta )=-\sqrt{2}\)
- Answer
-
\(\dfrac{3\pi }{12}, \dfrac{5\pi }{12}, \dfrac{11\pi }{12}, \dfrac{13\pi }{12}, \dfrac{19\pi }{12}, \dfrac{21\pi }{12}\)
20) \(\cos (2\theta )=-\dfrac{\sqrt{3}}{2}\)
21) \(2\sin(\pi \theta )=1\)
- Answer
-
\(\dfrac{1}{6}, \dfrac{5}{6}, \dfrac{13}{6}, \dfrac{17}{6}, \dfrac{25}{6}, \dfrac{29}{6}, \dfrac{37}{6}\)
22) \(2\cos \left(\dfrac{\pi }{5}\theta \right)=\sqrt{3}\)
For the exercises 23-32, find all exact solutions on \([0,2\pi )\)
23) \(\sec(x)\sin(x)-2\sin(x)=0\)
- Answer
-
\(0, \dfrac{\pi }{3}, \pi , \dfrac{5\pi }{3}\)
24) \(\tan(x)-2\sin(x)\tan(x)=0\)
25) \(2\cos^2 t+\cos(t)=1\)
- Answer
-
\(\dfrac{\pi }{3}, \pi , \dfrac{5\pi }{3}\)
26) \(2\tan^2(t)=3\sec(t)\)
27) \(2\sin(x)\cos(x)-\sin(x)+2\cos(x)-1=0\)
- Answer
-
\(\dfrac{\pi }{3}, \dfrac{3\pi }{2}, \dfrac{5\pi }{3}\)
28) \(\cos^2\theta =\dfrac{1}{2}\)
29) \(\sec^2 x =1\)
- Answer
-
\(0, \pi \)
30) \(\tan^2(x)=-1+2\tan(-x)\)
31) \(8\sin^2(x)+6\sin(x)+1=0\)
- Answer
-
\(\pi -\sin^{-1}\left ( -\dfrac{1}{4} \right ), \dfrac{7\pi }{6}, \dfrac{11\pi }{6}, 2\pi +\sin^{-1}\left ( -\dfrac{1}{4} \right )\)
32) \(\tan^5(x)=\tan(x)\)
For the exercises 33-40, solve with the methods shown in this section exactly on the interval \([0,2\pi )\)
33) \(\sin(3x)\cos(6x)-\cos(3x)\sin(6x)=-0.9\)
- Answer
-
\(\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{\pi }{3}-\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{2\pi }{3}+\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \pi -\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{4\pi }{3}+\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{5\pi }{3}-\)
34) \(\sin(6x)\cos(11x)-\cos(6x)\sin(11x)=-0.1\)
35) \(\cos(2x)\cos x+\sin(2x)\sin x=1\)
- Answer
-
\(0\)
36) \(6\sin(2t)+9\sin t=0\)
37) \(9\cos(2\theta )=9\cos^2\theta -4\)
- Answer
-
\(\dfrac{\pi }{6}, \dfrac{5\pi }{6}, \dfrac{7\pi }{6}, \dfrac{11\pi }{6}\)
38) \(\sin(2t)=\cos t\)
39) \(\cos(2t)=\sin t\)
- Answer
-
\(\dfrac{3\pi }{2}, \dfrac{\pi }{6}, \dfrac{5\pi }{6}\)
40) \(\cos(6x)-\cos(3x)=0\)
For the exercises 41-49, solve exactly on the interval \([0,2\pi )\)
41) \(\tan^2 x-\sqrt{3}\tan x=0\)
- Answer
-
\(0, \dfrac{\pi }{3}, \pi , \dfrac{4\pi }{3}\)
42) \(\sin^2 x+\sin x-2=0\)
43) \(\sin^2 x-2\sin x-4=0\)
- Answer
-
There are no solutions.
44) \(5\cos^2 x+3\cos x-1=0\)
45) \(3\cos^2 x-3\cos x-2=0\)
- Answer
-
\(\cos^{-1}\left (\dfrac{1}{3}\left ( 1-\sqrt{7} \right ) \right ), 2\pi -\cos^{-1}\left (\dfrac{1}{3}\left ( 1-\sqrt{7} \right ) \right )\)
46) \(5\sin^2 x+2\sin x-1=0\)
47) \(\tan^2 x+5\tan x-1=0\)
- Answer
-
\(\tan^{-1}\left (\dfrac{1}{2}\left ( \sqrt{29}-5 \right ) \right ), \pi +\tan^{-1}\left (\dfrac{1}{2}\left ( -\sqrt{29}-5 \right ) \right ), \pi +\tan^{-1}\left (\dfrac{1}{2}\left ( \sqrt{29}-5 \right ) \right ), 2\pi +\tan^{-1}\left (\dfrac{1}{2}\left ( -\sqrt{29}-5 \right ) \right )\)
48) \(\cot^2 x=-\cot x\)
49) \(-\tan^2 x-\tan x-2=0\)
- Answer
-
There are no solutions.
For the exercises 50-65, find exact solutions on the interval \([0,2\pi )\)
50) \(\sin^2 x-\cos^2 x-\sin x=0\)
51) \(\sin^2 x+\cos^2 x=0\)
- Answer
-
There are no solutions.
52) \(\sin(2x)-\sin x=0\)
53) \(\cos(2x)-\cos x=0\)
- Answer
-
\(0, \dfrac{2\pi }{3}, \dfrac{4\pi }{3}\)
54) \(\dfrac{2\tan x}{2-\sec ^2 x}-\sin^2 x=\cos^2 x\)
55) \(1-\cos(2x)=1+\cos(2x)\)
- Answer
-
\(\dfrac{\pi }{4}, \dfrac{3\pi }{4}, \dfrac{5\pi }{4}, \dfrac{7\pi }{4}\)
56) \(\sec^2 x=7\)
57) \(10\sin x \cos x=6 \cos x\)
- Answer
-
\(\sin^{-1}\left ( \dfrac{3}{5} \right ), \dfrac{\pi }{2}, \pi -\sin^{-1}\left ( \dfrac{3}{5} \right ), \dfrac{3\pi }{2}\)
58) \(-3\sin t=15\cos t \sin t\)
59) \(4\cos^2x - 4 = 15\cos x\)
- Answer
-
\(\cos^{-1}\left ( -\dfrac{1}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{1}{4} \right )\)
60) \(8\sin^2 x+6\sin x+1=0\)
61) \(8\cos^2 \theta =3-2\cos \theta\)
- Answer
-
\(\dfrac{\pi }{3}, \cos^{-1}\left ( -\dfrac{3}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{3}{4} \right ), \dfrac{5\pi }{3}\)
62) \(6\cos^2 x+7\sin x-8=0\)
63) \(12\sin^2 t+\cos t-6=0\)
- Answer
-
\(\cos^{-1}\left ( \dfrac{3}{4} \right ), \cos^{-1}\left ( -\dfrac{2}{3} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{2}{3} \right ), 2\pi -\cos^{-1}\left ( \dfrac{3}{4} \right )\)
64) \(\tan x=3\sin x\)
65) \(\cos^3 t=\cos t\)
- Answer
-
\(0, \dfrac{\pi }{2}, \pi , \dfrac{3\pi }{2}\)
Graphical
For the exercises 66-72, algebraically determine all solutions of the trigonometric equation exactly, then verify the results by graphing the equation and finding the zeros.
66) \(6\sin^2 x-5\sin x+1=0\)
67) \(8\cos^2 x-2\cos x-1=0\)
- Answer
-
\(\dfrac{\pi }{3}, \cos^{-1}\left ( -\dfrac{1}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{1}{4} \right ), \dfrac{5\pi }{3}\)
68) \(100\tan^2x+20\tan x-3=0\)
69) \(2\cos^2 x-\cos x+15=0\)
- Answer
-
There are no solutions.
70) \(20\sin^2 x-27\sin x+7=0\)
71) \(2\tan^2 x+7\tan x+6=0\)
- Answer
-
\(\pi +\tan^{-1}(-2), \pi +\tan^{-1}\left (-\dfrac{3}{2}\right ), 2\pi +\tan^{-1}(-2), 2\pi +\tan^{-1}\left (-\dfrac{3}{2} \right )\)
72) \(130\tan^2 x+69\tan x-130=0\)
Technology
For the exercises 73-76, use a calculator to find all solutions to four decimal places.
73) \(\sin x=0.27\)
- Answer
-
\(2\pi k+0.2734, 2\pi k+2.8682\)
74) \(\sin x=-0.55\)
75) \(\tan x=-0.34\)
- Answer
-
\(\pi k-0.3277\)
76) \(\cos x=0.71\)
77) \(\tan^2 x+3\tan x-3=0\)
- Answer
-
\(0.6694,1.8287,3.8110,4.9703\)
78) \(6\tan^2 x+13\tan x=-6\)
79) \(\tan^2 x-\sec x=1\)
- Answer
-
\(1.0472,3.1416,5.2360\)
80) \(\sin^2 x-2\cos^2 x=0\)
81) \(2\tan^2 x+9\tan x-6=0\)
- Answer
-
\(0.5326,1.7648,3.6742,4.9064\)
82) \(4\sin^2 x+\sin(2x)\sec x-3=0\)
Extensions
For the exercises 83-92, find all solutions exactly to the equations on the interval \([0,2\pi )\).
83) \(\csc^2 x-3\csc x-4=0\)
- Answer
-
\(\sin^{-1}\left ( \dfrac{1}{4} \right ), \pi -\sin^{-1}\left ( \dfrac{1}{4} \right ), \dfrac{3\pi }{2}\)
84) \(\sin^2 x-\cos^2 x-1=0\)
85) \(\sin^2 x(1-\sin^2 x)+\cos^2 x(1-\sin^2 x)=0\)
- Answer
-
\(\dfrac{\pi }{2}, \dfrac{3\pi }{2}\)
86) \(3\sec^2 x+2+\sin^2 x-\tan^2 x+\cos^2 x=0\)
87) \(\sin^2 x-1+2\cos(2x)-\cos^2 x=1\)
- Answer
-
There are no solutions.
88) \(\tan^2 x-1-\sec^3 x \cos x=0\)
89) \(\dfrac{\sin (2x)}{\sec ^2 x}=0\)
- Answer
-
\(0, \dfrac{\pi }{2}, \pi , \dfrac{3\pi }{2}\)
90) \(\dfrac{\sin (2x)}{2\csc ^2 x}=0\)
91) \(2\cos^2 x-\sin^2 x-\cos x-5=0\)
- Answer
-
There are no solutions.
92) \(\dfrac{1}{\sec ^2 x}+2+\sin ^2 x+4\cos ^2 x=4\)
Real-World Applications
93) An airplane has only enough gas to fly to a city \(200\) miles northeast of its current location. If the pilot knows that the city is \(25\) miles north, how many degrees north of east should the airplane fly?
- Answer
-
\(7.2^{\circ}\)
94) If a loading ramp is placed next to a truck, at a height of \(4\) feet, and the ramp is \(15\) feet long, what angle does the ramp make with the ground?
95) If a loading ramp is placed next to a truck, at a height of \(2\) feet, and the ramp is \(20\) feet long, what angle does the ramp make with the ground?
- Answer
-
\(5.7^{\circ}\)
96) A woman is watching a launched rocket currently \(11\) miles in altitude. If she is standing \(4\) miles from the launch pad, at what angle is she looking up from horizontal?
97) An astronaut is in a launched rocket currently \(15\) miles in altitude. If a man is standing \(2\) miles from the launch pad, at what angle is she looking down at him from horizontal? (Hint: this is called the angle of depression.)
- Answer
-
\(82.4^{\circ}\)
98) A woman is standing \(8\) meters away from a \(10\)-meter tall building. At what angle is she looking to the top of the building?
99) A man is standing \(10\) meters away from a \(6\)-meter tall building. Someone at the top of the building is looking down at him. At what angle is the person looking at him?
- Answer
-
\(31.0^{\circ}\)
100) A \(20\)-foot tall building has a shadow that is \(55\) feet long. What is the angle of elevation of the sun?
101) A \(90\)-foot tall building has a shadow that is \(2\) feet long. What is the angle of elevation of the sun?
- Answer
-
\(88.7^{\circ}\)
102) A spotlight on the ground \(3\) meters from a \(2\)-meter tall man casts a \(6\) meter shadow on a wall \(6\) meters from the man. At what angle is the light?
103) A spotlight on the ground \(3\) feet from a \(5\)-foot tall woman casts a \(15\)-foot tall shadow on a wall \(6\) feet from the woman. At what angle is the light?
- Answer
-
\(59.0^{\circ}\)
For the exercises 104-106, find a solution to the word problem algebraically. Then use a calculator to verify the result. Round the answer to the nearest tenth of a degree.
104) A person does a handstand with his feet touching a wall and his hands \(1.5\) feet away from the wall. If the person is \(6\) feet tall, what angle do his feet make with the wall?
105) A person does a handstand with her feet touching a wall and her hands \(3\) feet away from the wall. If the person is \(5\) feet tall, what angle do her feet make with the wall?
- Answer
-
\(36.9^{\circ}\)
106) A \(23\)-foot ladder is positioned next to a house. If the ladder slips at \(7\) feet from the house when there is not enough traction, what angle should the ladder make with the ground to avoid slipping?
7.6: Modeling with Trigonometric Equations
Many natural phenomena are also periodic. For example, the phases of the moon have a period of approximately \(28\) days, and birds know to fly south at about the same time each year. So how can we model an equation to reflect periodic behavior? First, we must collect and record data. We then find a function that resembles an observed pattern and alter the function to get a dependable model. Here. we will take a deeper look at specific types of periodic behavior and model equations to fit data.
Verbal
1) Explain what types of physical phenomena are best modeled by sinusoidal functions. What are the characteristics necessary?
- Answer
-
Physical behavior should be periodic, or cyclical.
2) What information is necessary to construct a trigonometric model of daily temperature? Give examples of two different sets of information that would enable modeling with an equation.
3) If we want to model cumulative rainfall over the course of a year, would a sinusoidal function be a good model? Why or why not?
- Answer
-
Since cumulative rainfall is always increasing, a sinusoidal function would not be ideal here.
4) Explain the effect of a damping factor on the graphs of harmonic motion functions.
Algebraic
For the exercises 5-13, find a possible formula for the trigonometric function represented by the given table of values.
5)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(−4\) |
| \(3\) | \(−1\) |
| \(6\) | \(2\) |
| \(9\) | \(−1\) |
| \(12\) | \(−4\) |
| \(15\) | \(−1\) |
| \(18\) | \(2\) |
- Answer
-
\(y=−3 \cos \left(\dfrac{π}{6}x \right)−1\)
6)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(5\) |
| \(2\) | \(1\) |
| \(4\) | \(−3\) |
| \(6\) | \(1\) |
| \(8\) | \(5\) |
| \(10\) | \(1\) |
| \(12\) | \(−3\) |
7)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(2\) |
| \(\frac{π}{4}\) | \(7\) |
| \(\frac{π}{2}\) | \(2\) |
| \(\frac{3π}{4}\) | \(−3\) |
| \(π\) | \(2\) |
| \(\frac{5π}{4}\) | \(7\) |
| \(\frac{3π}{2}\) | \(2\) |
- Answer
-
\(5 \sin (2x)+2\)
8)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(2\) |
| \(\frac{π}{4}\) | \(7\) |
| \(\frac{π}{2}\) | \(2\) |
| \(\frac{3π}{4}\) | \(−3\) |
| \(π\) | \(2\) |
| \(\frac{5π}{4}\) | \(7\) |
| \(\frac{3π}{2}\) | \(2\) |
9)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(1\) |
| \(1\) | \(−3\) |
| \(2\) | \(−7\) |
| \(3\) | \(−3\) |
| \(4\) | \(1\) |
| \(5\) | \(−3\) |
| \(6\) | \(−7\) |
- Answer
-
\(4\cos \left(\dfrac{xπ}{2} \right)−3\)
10)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(−2\) |
| \(1\) | \(4\) |
| \(2\) | \(10\) |
| \(3\) | \(4\) |
| \(4\) | \(−2\) |
| \(5\) | \(4\) |
| \(6\) | \(10\) |
11)
| \(x\) | \(y\) |
|---|---|
| \(0\) | \(5\) |
| \(1\) | \(-3\) |
| \(2\) | \(5\) |
| \(3\) | \(13\) |
| \(4\) | \(5\) |
| \(5\) | \(-3\) |
| \(6\) | \(5\) |
- Answer
-
\(5−8 \sin \left(\dfrac{xπ}{2} \right)\)
12)
| \(x\) | \(y\) |
|---|---|
| \(−3\) | \(−1−\sqrt{2}\) |
| \(−2\) | \(−1\) |
| \(−1\) | \(1−\sqrt{2}\) |
| \(0\) | \(0\) |
| \(1\) | \(\sqrt{2}−1\) |
| \(2\) | \(1\) |
| \(3\) | \(\sqrt{2}+1\) |
13)
| \(x\) | \(y\) |
|---|---|
| \(−1\) | \(\sqrt{3}−2\) |
| \(0\) | \(0\) |
| \(1\) | \(2−\sqrt{3}\) |
| \(2\) | \(\frac{\sqrt{3}}{3}\) |
| \(3\) | \(1\) |
| \(4\) | \(\sqrt{3}\) |
| \(5\) | \(2+\sqrt{3}\) |
- Answer
-
\(\tan \left(\dfrac{xπ}{12} \right)\)
Graphical
For the exercises 14-16, graph the given function, and then find a possible physical process that the equation could model.
14) \(f(x)=−30 \cos \left(\dfrac{xπ}{6} \right)−20 \cos ^2 \left(\dfrac{xπ}{6} \right)+80 \; [0,12]\)
15) \(f(x)=−18 \cos \left(\dfrac{xπ}{12} \right)−5 \sin \left(\dfrac{xπ}{12} \right)+100\) on the interval \([0,24]\)
- Answer
-
![Graph of f(x) = -18cos(x*pi/12) - 5sin(x*pi/12) + 100 on the interval [0,24]. There is a single peak around 12.](https://math.libretexts.org/@api/deki/files/7325/CNX_Precalc_Figure_07_06_202.jpg?revision=1)
Answers will vary. Sample answer: This function could model temperature changes over the course of one very hot day in Phoenix, Arizona.
16) \(f(x)=10−\sin \left(\dfrac{xπ}{6} \right)+24 \tan \left(\dfrac{xπ}{240} \right)\) on the interval \([0,80]\)
Technology
For the exercise 17, construct a function modeling behavior and use a calculator to find desired results.
17) A city’s average yearly rainfall is currently \(20\) inches and varies seasonally by \(5\) inches. Due to unforeseen circumstances, rainfall appears to be decreasing by \(15\%\) each year. How many years from now would we expect rainfall to initially reach \(0\) inches? Note, the model is invalid once it predicts negative rainfall, so choose the first point at which it goes below \(0\).
- Answer
-
\(9\) years from now
Real-World Applications
For the exercises 18-29, construct a sinusoidal function with the provided information, and then solve the equation for the requested values.
18) Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the high temperature of \(105°F\) occurs at 5PM and the average temperature for the day is \(85°F\). Find the temperature, to the nearest degree, at 9AM.
19) Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the high temperature of \(84°F\) occurs at 6PM and the average temperature for the day is \(70°F.\) Find the temperature, to the nearest degree, at 7AM.
- Answer
-
\(56 °F\)
20) Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the temperature varies between \(47°F\) and \(63°F\) during the day and the average daily temperature first occurs at 10 AM. How many hours after midnight does the temperature first reach \(51°F\)?
21) Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the temperature varies between \(64°F\) and \(86°F\) during the day and the average daily temperature first occurs at 12 AM. How many hours after midnight does the temperature first reach \(70°F\)?
- Answer
-
\(1.8024\) hours
22) A Ferris wheel is \(20\) meters in diameter and boarded from a platform that is \(2\) meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes \(1\) full revolution in \(6\) minutes. How much of the ride, in minutes and seconds, is spent higher than \(13\) meters above the ground?
23)A Ferris wheel is \(45\) meters in diameter and boarded from a platform that is \(1\) meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes \(1\) full revolution in \(10\) minutes. How many minutes of the ride are spent higher than \(27\) meters above the ground? Round to the nearest second.
- Answer
-
\(4:30\)
24) The sea ice area around the North Pole fluctuates between about \(6\) million square kilometers on September 1 to \(14\) million square kilometers on March 1. Assuming a sinusoidal fluctuation, when are there less than 9 million square kilometers of sea ice? Give your answer as a range of dates, to the nearest day.
25) The sea ice area around the South Pole fluctuates between about \(18\) million square kilometers in September to \(3\) million square kilometers in March. Assuming a sinusoidal fluctuation, when are there more than 15 million square kilometers of sea ice? Give your answer as a range of dates, to the nearest day.
- Answer
-
From July 8 to October 23
26) During a \(90\)-day monsoon season, daily rainfall can be modeled by sinusoidal functions. If the rainfall fluctuates between a low of \(2\) inches on day \(10\) and \(12\) inches on day \(55\), during what period is daily rainfall more than \(10\) inches?
27) During a \(90\)-day monsoon season, daily rainfall can be modeled by sinusoidal functions. A low of \(4\) inches of rainfall was recorded on day \(30\), and overall the average daily rainfall was \(8\) inches. During what period was daily rainfall less than \(5\) inches?
- Answer
-
From day \(19\) through day \(40\)
28) In a certain region, monthly precipitation peaks at \(8\) inches on June 1 and falls to a low of \(1\) inch on December 1. Identify the periods when the region is under flood conditions (greater than \(7\) inches) and drought conditions (less than \(2\) inches). Give your answer in terms of the nearest day.
29) In a certain region, monthly precipitation peaks at \(24\) inches in September and falls to a low of \(4\) inches in March. Identify the periods when the region is under flood conditions (greater than \(22\) inches) and drought conditions (less than \(5\) inches). Give your answer in terms of the nearest day.
- Answer
-
Floods: July 24 through October 7. Droughts: February 4 through March 27
For the exercises 30-32, find the amplitude, period, and frequency of the given function.
30) The displacement \(h(t)\) in centimeters of a mass suspended by a spring is modeled by the function \(h(t)=8 \sin (6πt),\) where \(t\) is measured in seconds. Find the amplitude, period, and frequency of this displacement.
31) The displacement \(h(t)\) in centimeters of a mass suspended by a spring is modeled by the function \(h(t)=11 \sin (12πt),\) where \(t\) is measured in seconds. Find the amplitude, period, and frequency of this displacement.
- Answer
-
Amplitude: \(11\), period: \(\dfrac{1}{6}\), frequency: \(6\) Hz
32) The displacement \(h(t)\) in centimeters of a mass suspended by a spring is modeled by the function \(h(t)=4 \cos \left(\dfrac{π}{2}t \right)\), where \(t\) is measured in seconds. Find the amplitude, period, and frequency of this displacement.
For the exercise 33, construct an equation that models the described behavior.
33) The displacement \(h(t)\), in centimeters, of a mass suspended by a spring is modeled by the function \(h(t)=−5 \cos (60πt)\), where \(t\) is measured in seconds. Find the amplitude, period, and frequency of this displacement.
- Answer
-
Amplitude: \(5\), period: \(\dfrac{1}{30}\), frequency: \(30\) Hz
For the exercises 34-41, construct an equation that models the described behavior.
34) A deer population oscillates \(19\) above and below average during the year, reaching the lowest value in January. The average population starts at \(800\) deer and increases by \(160\) each year. Find a function that models the population, \(P\), in terms of months since January, \(t\).
35) A rabbit population oscillates \(15\) above and below average during the year, reaching the lowest value in January. The average population starts at \(650\) rabbits and increases by \(110\) each year. Find a function that models the population, \(P\), in terms of months since January, \(t\).
- Answer
-
\(P(t)=−15 \cos \left(\dfrac{π}{6}t \right)+650+\dfrac{55}{6}t\)
36) A muskrat population oscillates \(33\) above and below average during the year, reaching the lowest value in January. The average population starts at \(900\) muskrats and increases by \(7\%\) each month. Find a function that models the population, \(P\), in terms of months since January, \(t\).
37) A fish population oscillates \(40\) above and below average during the year, reaching the lowest value in January. The average population starts at \(800\) fish and increases by \(4\%\) each month. Find a function that models the population, \(P\), in terms of months since January, \(t\).
- Answer
-
\(P(t)=−40 \cos \left(\dfrac{π}{6}t \right)+800(1.04)^t\)
38) A spring attached to the ceiling is pulled \(10\) cm down from equilibrium and released. The amplitude decreases by \(15\%\) each second. The spring oscillates \(18\) times each second. Find a function that models the distance, \(D\), the end of the spring is from equilibrium in terms of seconds, \(t\), since the spring was released.
39) A spring attached to the ceiling is pulled \(7\) cm down from equilibrium and released. The amplitude decreases by \(11\%\) each second. The spring oscillates \(20\) times each second. Find a function that models the distance, \(D\), the end of the spring is from equilibrium in terms of seconds, \(t,\) since the spring was released.
- Answer
-
\(D(t)=7(0.89)^t \cos (40πt)\)
40) A spring attached to the ceiling is pulled \(17\) cm down from equilibrium and released. After \(3\) seconds, the amplitude has decreased to \(13\) cm. The spring oscillates \(14\) times each second. Find a function that models the distance, \(D,\) the end of the spring is from equilibrium in terms of seconds, \(t\), since the spring was released.
41) A spring attached to the ceiling is pulled \(19\) cm down from equilibrium and released. After \(4\) seconds, the amplitude has decreased to \(14\) cm. The spring oscillates \(13\) times each second. Find a function that models the distance, \(D\), the end of the spring is from equilibrium in terms of seconds, \(t\), since the spring was released.
- Answer
-
\(D(t)=19(0.9265)^t \cos (26πt)\)
For the exercises 42-47, create a function modeling the described behavior. Then, calculate the desired result using a calculator.
42) A certain lake currently has an average trout population of \(20,000\). The population naturally oscillates above and below average by \(2,000\) every year. This year, the lake was opened to fishermen. If fishermen catch \(3,000\) fish every year, how long will it take for the lake to have no more trout?
43) Whitefish populations are currently at \(500\) in a lake. The population naturally oscillates above and below by \(25\) each year. If humans overfish, taking \(4\%\) of the population every year, in how many years will the lake first have fewer than \(200\) whitefish?
- Answer
-
\(20.1\) years
44) A spring attached to a ceiling is pulled down \(11\) cm from equilibrium and released. After \(2\) seconds, the amplitude has decreased to \(6\) cm. The spring oscillates \(8\) times each second. Find when the spring first comes between \(−0.1\) and \(0.1\) cm, effectively at rest.
45) A spring attached to a ceiling is pulled down \(21\) cm from equilibrium and released. After \(6\) seconds, the amplitude has decreased to \(4\) cm. The spring oscillates \(20\) times each second. Find when the spring first comes between \(−0.1\) and \(0.1\) cm, effectively at rest.
- Answer
-
\(17.8\) seconds
46) Two springs are pulled down from the ceiling and released at the same time. The first spring, which oscillates \(8\) times per second, was initially pulled down \(32\) cm from equilibrium, and the amplitude decreases by \(50\%\) each second. The second spring, oscillating \(18\) times per second, was initially pulled down \(15\) cm from equilibrium and after \(4\) seconds has an amplitude of \(2\) cm. Which spring comes to rest first, and at what time? Consider “rest” as an amplitude less than \(0.1\) cm.
47) Two springs are pulled down from the ceiling and released at the same time. The first spring, which oscillates \(14\) times per second, was initially pulled down \(2\) cm from equilibrium, and the amplitude decreases by \(8\%\) each second. The second spring, oscillating \(22\) times per second, was initially pulled down \(10\) cm from equilibrium and after \(3\) seconds has an amplitude of \(2\) cm. Which spring comes to rest first, and at what time? Consider “rest” as an amplitude less than \(0.1\) cm.
- Answer
-
Spring 2 comes to rest first after \(8.0\) seconds.
Extensions
48) A plane flies \(1\) hour at \(150\) mph at \(22^∘\) east of north, then continues to fly for \(1.5\) hours at \(120\) mph, this time at a bearing of \(112^∘\) east of north. Find the total distance from the starting point and the direct angle flown north of east.
49) A plane flies \(2\) hours at \(200\) mph at a bearing of \(60^∘\),then continues to fly for \(1.5\) hours at the same speed, this time at a bearing of \(150^∘\). Find the distance from the starting point and the bearing from the starting point. (Hint: bearing is measured counterclockwise from north.)
- Answer
-
\(500\) miles, at \(90^∘\)
For the exercises 50-52, find a function of the form \(y=ab^x \sin \left(\dfrac{π}{2}x \right)+c\) that fits the given data.
50)
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(y\) | 6 | 29 | 96 | 379 |
51)
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(y\) | 6 | 34 | 150 | 746 |
- Answer
-
\(y=6(5)^x+4 \sin \left(\dfrac{π}{2}x \right)\)
52)
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(y\) | 4 | 0 | 16 | -40 |
For the exercises 53-54, find a function of the form \(y=ab^x \cos \left(\dfrac{π}{2}x \right)+c\) that fits the given data.
53)
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(y\) | 11 | 3 | 1 | 3 |
- Answer
-
\(y=8\left(\dfrac{1}{2} \right)^x \cos \left(\dfrac{π}{2}x \right)+3\)
54)
| \(x\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(y\) | 4 | 1 | −11 | 1 |
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

