11.3: Geometric Sequences
- Last updated
- Save as PDF
- Page ID
- 13566
Learning Objectives
- Find the common ratio for a geometric sequence.
- List the terms of a geometric sequence.
- Use a recursive formula for a geometric sequence.
- Use an explicit formula for a geometric sequence.
Many jobs offer an annual cost-of-living increase to keep salaries consistent with inflation. Suppose, for example, a recent college graduate finds a position as a sales manager earning an annual salary of \($26,000\). He is promised a \(2\%\) cost of living increase each year. His annual salary in any given year can be found by multiplying his salary from the previous year by \(102\%\). His salary will be \($26,520\) after one year; \($27,050.40\) after two years; \($27,591.41\) after three years; and so on. When a salary increases by a constant rate each year, the salary grows by a constant factor. In this section, we will review sequences that grow in this way.
Finding Common Ratios
The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio. The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term.

Definition: GEOMETRIC SEQUENCE
A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence. The common ratio can be found by dividing any term in the sequence by the previous term. If \(a_1\) is the initial term of a geometric sequence and \(r\) is the common ratio, the sequence will be
\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]
How to: Given a set of numbers, determine if they represent a geometric sequence.
- Divide each term by the previous term.
- Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.
Example \(\PageIndex{1}\): Finding Common Ratios
Is the sequence geometric? If so, find the common ratio.
- \(1\), \(2\), \(4\), \(8\), \(16\),...
- \(48\), \(12\), \(4\), \(2\),...
Solution
Divide each term by the previous term to determine whether a common ratio exists.
- \(\dfrac{2}{1}=2\) \(\dfrac{4}{2}=2\) \(\dfrac{8}{4}=2\) \(\dfrac{16}{8}=2\)
The sequence is geometric because there is a common ratio. The common ratio is \(2\).
- \(\dfrac{12}{48}=\dfrac{1}{4}\) \(\dfrac{4}{12}=\dfrac{1}{3}\) \(\dfrac{2}{4}=\dfrac{1}{2}\)
The sequence is not geometric because there is not a common ratio.
Analysis
The graph of each sequence is shown in Figure \(\PageIndex{1}\). It seems from the graphs that both (a) and (b) appear have the form of the graph of an exponential function in this viewing window. However, we know that (a) is geometric and so this interpretation holds, but (b) is not.
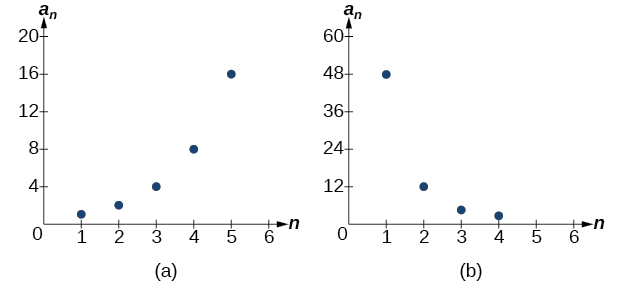
Figure \(\PageIndex{1}\)
Q&A
If you are told that a sequence is geometric, do you have to divide every term by the previous term to find the common ratio?
No. If you know that the sequence is geometric, you can choose any one term in the sequence and divide it by the previous term to find the common ratio.
Exercise \(\PageIndex{1A}\)
Is the sequence geometric? If so, find the common ratio.
\(5\), \(10\), \(15\), \(20\),...
- Answer
-
The sequence is not geometric because \(\dfrac{10}{5}≠\dfrac{15}{10}\)
Exercise \(\PageIndex{1B}\)
Is the sequence geometric? If so, find the common ratio.
\(100\), \(20\), \(4\), \(\dfrac{4}{5}\),...
- Answer
-
The sequence is geometric. The common ratio is \(\dfrac{1}{5}\)
Writing Terms of Geometric Sequences
Now that we can identify a geometric sequence, we will learn how to find the terms of a geometric sequence if we are given the first term and the common ratio. The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. For instance, if the first term of a geometric sequence is \(a_1=−2\) and the common ratio is \(r=4\), we can find subsequent terms by multiplying \(−2⋅4\) to get \(−8\) then multiplying the result \(−8⋅4\) to get \(−32\) and so on.
\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]
The first four terms are \(\{–2, –8, –32, –128\}\).
How to: Given the first term and the common factor, find the first four terms of a geometric sequence.
- Multiply the initial term, \(a_1\), by the common ratio to find the next term, \(a_2\).
- Repeat the process, using \(a_n=a_2\) to find \(a_3\) and then use \(a_3\) to find \(a_4\), until all four terms have been identified.
- Write the terms separated by commons within brackets.
Example \(\PageIndex{2}\): Writing the Terms of a Geometric Sequence
List the first four terms of the geometric sequence with \(a_1=5\) and \(r=–2\).
Solution
Multiply \(a_1\) by \(−2\) to find \(a_2\). Repeat the process, using \(a_2\) to find \(a_3\), and so on.
\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]
The first four terms are \(\{5,–10,20,–40\}\).
Exercise \(\PageIndex{2}\)
List the first five terms of the geometric sequence with \(a_1=18\) and \(r=\dfrac{1}{3}\).
- Answer
-
\(\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} \)
Using Recursive Formulas for Geometric Sequences
A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is \(9\). Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.
Note: RECURSIVE FORMULA FOR A GEOMETRIC SEQUENCE
The recursive formula for a geometric sequence with common ratio r and first term \(a_1\) is
\[a_n=ra_{n−1},\;\;\; n≥2\]
How to: Given the first several terms of a geometric sequence, write its recursive formula.
- State the initial term.
- Find the common ratio by dividing any term by the preceding term.
- Substitute the common ratio into the recursive formula for a geometric sequence.
Example \(\PageIndex{3}\): Using Recursive Formulas for Geometric Sequences
Write a recursive formula for the following geometric sequence.
\(\{6, 9, 13.5, 20.25, ...\} \nonumber\)
Solution
The first term is given as \(6\). The common ratio can be found by dividing the second term by the first term.
\(r=\dfrac{9}{6}=1.5 \nonumber\)
Substitute the common ratio into the recursive formula for geometric sequences and define \(a_1\).
\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]
Analysis
The sequence of data points follows an exponential pattern. The common ratio is also the base of an exponential function as shown in Figure \(\PageIndex{2}\).
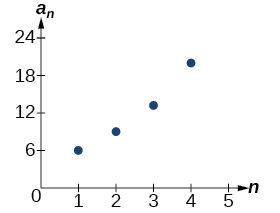
Figure \(\PageIndex{2}\)
Q&A
Do we have to divide the second term by the first term to find the common ratio?
No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.
Exercise \(\PageIndex{3}\)
Write a recursive formula for the following geometric sequence.
\(\{2, 43, 89, 1627, ...\}\)
- Answer
-
\(\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}\)
Using Explicit Formulas for Geometric Sequences
Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.
\[a_n=a_1r^{n−1}\]
Let’s take a look at the sequence \(\{18, 36, 72, 144, 288, ...\}\). This is a geometric sequence with a common ratio of \(2\) and an exponential function with a base of \(2\). An explicit formula for this sequence is
\(a_n=18·2^{n−1}\)
The graph of the sequence is shown in Figure \(\PageIndex{3}\).
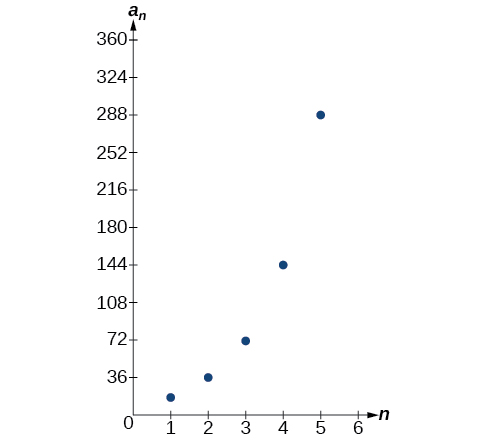
Figure \(\PageIndex{3}\)
Note: EXPLICIT FORMULA FOR A GEOMETRIC SEQUENCE
The \(n^{th}\) term of a geometric sequence is given by the explicit formula:
\[a_n=a_1r^{n−1}\]
Example \(\PageIndex{4}\): Writing Terms of Geometric Sequences Using the Explicit Formula
Given a geometric sequence with \(a_1=3\) and \(a_4=24\), find \(a_2\).
Solution
The sequence can be written in terms of the initial term and the common ratio \(r\).
\(3\), \(3r\), \(3r^2\), \(3r^3\),...
Find the common ratio using the given fourth term.
\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]
Find the second term by multiplying the first term by the common ratio.
\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]
Analysis
The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power.
Exercise \(\PageIndex{4}\)
Given a geometric sequence with \(a_2=4\) and \(2a_3=32\), find \(a_6\).
- Answer
-
\(a_6=16,384\)
Example \(\PageIndex{5}\): Writing an Explicit Formula for the nth Term of a Geometric Sequence
Write an explicit formula for the nth term of the following geometric sequence.
\(\{2, 10, 50, 250, ...\}\)
Solution
The first term is \(2\). The common ratio can be found by dividing the second term by the first term.
\(\dfrac{10}{2}=5\)
The common ratio is \(5\). Substitute the common ratio and the first term of the sequence into the formula.
\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]
The graph of this sequence in Figure \(\PageIndex{4}\) shows an exponential pattern.
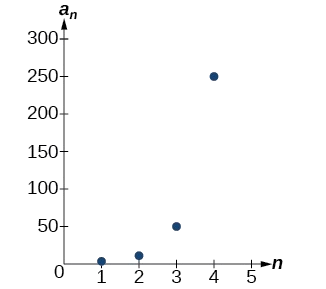
Figure \(\PageIndex{4}\)
Exercise \(\PageIndex{5}\)
Write an explicit formula for the following geometric sequence.
\(\{–1, 3, –9, 27, ...\}\)
- Answer
-
\(a_n=−{(−3)}^{n−1}\)
Solving Application Problems with Geometric Sequences
In real-world scenarios involving arithmetic sequences, we may need to use an initial term of \(a_0\) instead of \(a_1\). In these problems, we can alter the explicit formula slightly by using the following formula:
\(a_n=a_0r^n\)
Example \(\PageIndex{6}\): Solving Application Problems with Geometric Sequences
In 2013, the number of students in a small school is \(284\). It is estimated that the student population will increase by \(4\%\) each year.
- Write a formula for the student population.
- Estimate the student population in 2020.
Solution
- The situation can be modeled by a geometric sequence with an initial term of \(284\). The student population will be \(104\%\) of the prior year, so the common ratio is \(1.04\).
Let \(P\) be the student population and \(n\) be the number of years after 2013. Using the explicit formula for a geometric sequence we get
\(P_n =284⋅{1.04}^n\)
- We can find the number of years since 2013 by subtracting.
\(2020−2013=7\)
We are looking for the population after \(7\) years. We can substitute \(7\) for \(n\) to estimate the population in 2020.
\(P_7=284⋅{1.04}^7≈374\)
The student population will be about \(374\) in 2020.
Exercise \(\PageIndex{6}\)
A business starts a new website. Initially the number of hits is \(293\) due to the curiosity factor. The business estimates the number of hits will increase by \(2.6%\) per week.
- Write a formula for the number of hits.
- Estimate the number of hits in \(5\) weeks.
- Answer a
-
\(P_n = 293⋅1.026a^n\)
- Answer b
-
The number of hits will be about \(333\).
Media
Access these online resources for additional instruction and practice with geometric sequences.
Key Equations
| recursive formula for nth term of a geometric sequence | \(a_n=ra_{n−1}\), \(n≥2\) |
| explicit formula for nth term of a geometric sequence | \(a_n=a_1r^{n−1}\) |
Key Concepts
- A geometric sequence is a sequence in which the ratio between any two consecutive terms is a constant.
- The constant ratio between two consecutive terms is called the common ratio.
- The common ratio can be found by dividing any term in the sequence by the previous term. See Example \(\PageIndex{1}\).
- The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{4}\).
- A recursive formula for a geometric sequence with common ratio \(r\) is given by \(a_n=ra_{n–1}\) for \(n≥2\).
- As with any recursive formula, the initial term of the sequence must be given. See Example \(\PageIndex{3}\).
- An explicit formula for a geometric sequence with common ratio \(r\) is given by \(a_n=a_1r^{n–1}\). See Example \(\PageIndex{5}\).
- In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0r^n\). See Example \(\PageIndex{6}\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


