14.E: Differentiation of Functions of Several Variables (Exercise)
- Page ID
- 4807
14.1: Functions of Several Variables
For the following exercises, evaluate each function at the indicated values.
1) \(\displaystyle W(x,y)=4x^2+y^2.\) Find \(\displaystyle W(2,−1), W(−3,6).\)
Solution:\(\displaystyle 17,72\)
2) \(\displaystyle W(x,y)=4x^2+y^2\). Find \(\displaystyle W(2+h,3+h).\)
3) The volume of a right circular cylinder is calculated by a function of two variables, \(\displaystyle V(x,y)=πx^2y,\) where \(\displaystyle x\) is the radius of the right circular cylinder and \(\displaystyle y\) represents the height of the cylinder. Evaluate \(\displaystyle V(2,5)\) and explain what this means.
Solution:\(\displaystyle 20π.\) This is the volume when the radius is \(\displaystyle 2\) and the height is \(\displaystyle 5\).
4) An oxygen tank is constructed of a right cylinder of height \(\displaystyle y\) and radius \(\displaystyle x\) with two hemispheres of radius \(\displaystyle x\) mounted on the top and bottom of the cylinder. Express the volume of the cylinder as a function of two variables, \(\displaystyle x\) and \(\displaystyle y\), find \(\displaystyle V(10,2)\), and explain what this means.
For the following exercises, find the domain of the function.
5) \(\displaystyle V(x,y)=4x^2+y^2\)
Solution:All points in the \(\displaystyle xy-plane\)
6) \(\displaystyle f(x,y)=sqrt{x^2+y^2−4}\)
7) \(\displaystyle f(x,y)=4ln(y^2−x)\)
Solution:\(\displaystyle x<y^2\)
8) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)
9) \(\displaystyle z(x,y)=y^2−x^2\)
Solution:All real ordered pairs in the \(\displaystyle xy-plane\) of the form \(\displaystyle (a,b)\)
10) \(\displaystyle f(x,y)=\frac{y+2}{x^2}\)
Find the range of the functions.
11) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)
Solution:\(\displaystyle {z|0≤z≤4}\)
12) \(\displaystyle V(x,y)=4x^2+y^2\)
13) \(\displaystyle z=y^2−x^2\)
Solution:The set \(\displaystyle R\)
For the following exercises, find the level curves of each function at the indicated value of \(\displaystyle c\) to visualize the given function.
14) \(\displaystyle z(x,y)=y^2−x^2, c=1\)
15) \(\displaystyle z(x,y)=y^2−x^2, c=4\)
Solution:\(\displaystyle y^2−x^2=4,\) a hyperbola
16) \(\displaystyle g(x,y)=x^2+y^2;c=4,c=9\)
17) \(\displaystyle g(x,y)=4−x−y;c=0,4\)
Solution:\(\displaystyle 4=x+y,\) a line; \(\displaystyle x+y=0,\) line through the origin
18) \(\displaystyle f(x,y)=xy;c=1;c=−1\)
19) \(\displaystyle h(x,y)=2x−y;c=0,−2,2\)
Solution:\(\displaystyle 2x−y=0,2x−y=−2,2x−y=2;\) three lines
20) \(\displaystyle f(x,y)=x^2−y;c=1,2\)
21) \(\displaystyle g(x,y)=\frac{x}{x+y};c=−1,0,2\)
Solution:\(\displaystyle \frac{x}{x+y}=−1,\frac{x}{x+y}=0,\frac{x}{x+y}=2\)
22) \(\displaystyle g(x,y)=x^3−y;c=−1,0,2\)
23) \(\displaystyle g(x,y)=e^{xy};c=\frac{1}{2},3\)
Solution:\(\displaystyle e^{xy}=\frac{1}{2},e^{xy}=3\)
24) \(\displaystyle f(x,y)=x^2;c=4,9\)
25) \(\displaystyle f(x,y)=xy−x;c=−2,0,2\)
Solution:\(\displaystyle xy−x=−2,xy−x=0,xy−x=2\)
26) \(\displaystyle h(x,y)=ln(x^2+y^2);c=−1,0,1\)
27) \(\displaystyle g(x,y)=ln(\frac{y}{x^2});c=−2,0,2\)
Solution:\(\displaystyle e^{−2}x^2=y,y=x^2,y=e^2x^2\)
28) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}, c=3\)
29) \(\displaystyle f(x,y)=\frac{y+2}{x^2}, c=\)any constant
Solution:The level curves are parabolas of the form \(\displaystyle y=cx^2−2.\)
For the following exercises, find the vertical traces of the functions at the indicated values of \(\displaystyle x\) and \(\displaystyle y\), and plot the traces.
30) \(\displaystyle z=4−x−y;x=2\)
31) \(\displaystyle f(x,y)=3x+y^3,x=1\)
Solution:\(\displaystyle z=3+y^3,\) a curve in the zy-plane with rulings parallel to the \(\displaystyle x-axis\)
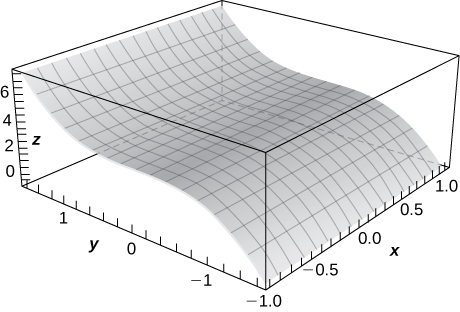
32) \(\displaystyle z=cos\sqrt{x^2+y^2} x=1\)
Find the domain of the following functions.
33) \(\displaystyle z=\sqrt{100−4x^2−25y^2}\)
Solution:\(\displaystyle \frac{x^2}{25}+\frac{y^2}{4}≤1\)
34) \(\displaystyle z=ln(x−y^2)\)
35) \(\displaystyle f(x,y,z)=\frac{1}{\sqrt{36−4x^2−9y^2−z^2}}\)
Solution:\(\displaystyle \frac{x^2}{9}+\frac{y^2}{4}+\frac{z^2}{36}<1\)
36) \(\displaystyle f(x,y,z)=\sqrt{49−x^2−y^2−z^2}\)
37) \(\displaystyle f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}\)
Solution:All points in \(\displaystyle xyz-space\)
38) \(\displaystyle f(x,y)=cos\sqrt{x^2+y^2}\)
For the following exercises, plot a graph of the function.
39) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}\)
Solution:
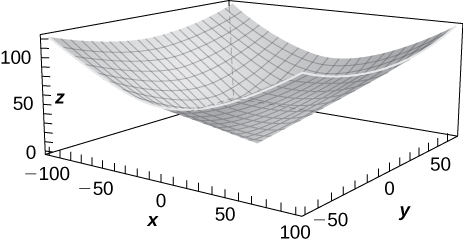
40) \(\displaystyle z=x^2+y^2\)
41) Use technology to graph \(\displaystyle z=x^2y.\)
Solution:
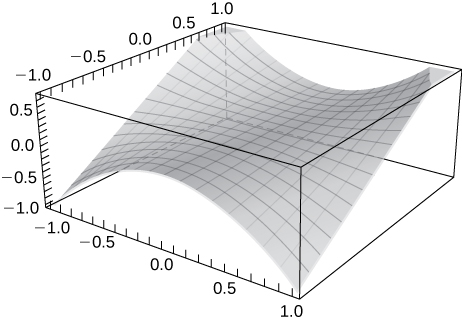
Sketch the following by finding the level curves. Verify the graph using technology.
42) \(\displaystyle f(x,y)=\sqrt{4−x^2−y^2}\)
43) \(\displaystyle f(x,y)=2−\sqrt{x^2+y^2}\)
Solution:
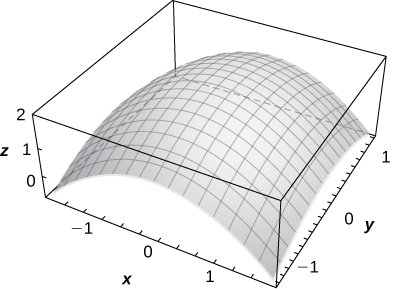
44) \(\displaystyle z=1+e^{−x^2−y^2}\)
45) \(\displaystyle z=cos\sqrt{x^2+y^2}\)
Solution:
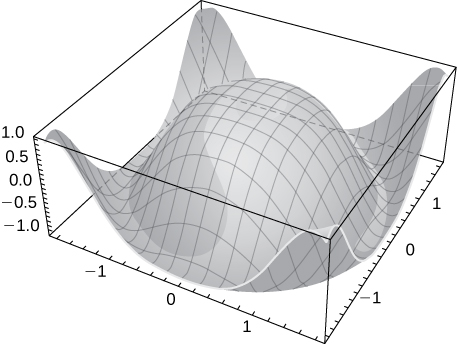
46) \(\displaystyle z=y^2−x^2\)
47) Describe the contour lines for several values of \(\displaystyle c\) for \(\displaystyle z=x^2+y^2−2x−2y.\)
Solution:The contour lines are circles.
Find the level surface for the functions of three variables and describe it.
48) \(\displaystyle w(x,y,z)=x−2y+z,c=4\)
49) \(\displaystyle w(x,y,z)=x^2+y^2+z^2,c=9\)
Solution:\(\displaystyle x^2+y^2+z^2=9\), a sphere of radius \(\displaystyle 3\)
50) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=−4\)
51) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=4\)
Solution:\(\displaystyle x^2+y^2−z^2=4,\) a hyperboloid of one sheet
52) \(\displaystyle w(x,y,z)=9x^2−4y^2+36z^2,c=0\)
For the following exercises, find an equation of the level curve of \(\displaystyle f\) that contains the point \(\displaystyle P\).
53) \(\displaystyle f(x,y)=1−4x^2−y^2,P(0,1)\)
Solution:\(\displaystyle 4x^2+y^2=1,\)
54) \(\displaystyle g(x,y)=y^2arctanx,P(1,2)\)
55) \(\displaystyle g(x,y)=e^{xy}(x^2+y^2),P(1,0)\)
Solution:\(\displaystyle 1=e^{xy}(x^2+y^2)\)
56) The strength \(\displaystyle E\) of an electric field at point \(\displaystyle (x,y,z)\) resulting from an infinitely long charged wire lying along the \(\displaystyle y-axis\) is given by \(\displaystyle E(x,y,z)=k/\sqrt{x^2+y^2}\), where \(\displaystyle k\) is a positive constant. For simplicity, let \(\displaystyle k=1\) and find the equations of the level surfaces for \(\displaystyle E=10\) and \(\displaystyle E=100.\)
57) A thin plate made of iron is located in the \(\displaystyle xy-plane.\) The temperature \(\displaystyle T\) in degrees Celsius at a point \(\displaystyle P(x,y)\) is inversely proportional to the square of its distance from the origin. Express \(\displaystyle T\) as a function of \(\displaystyle x\) and \(\displaystyle y\).
Solution:\(\displaystyle T(x,y)=\frac{k}{x^2+y^2}\)
58) Refer to the preceding problem. Using the temperature function found there, determine the proportionality constant if the temperature at point \(\displaystyle P(1,2)\) is \(\displaystyle 50°C.\) Use this constant to determine the temperature at point \(\displaystyle Q(3,4).\)
59) Refer to the preceding problem. Find the level curves for \(\displaystyle T=40°C\) and \(\displaystyle T=100°C,\) and describe what the level curves represent.
Solution:\(\displaystyle x^2+y^2=\frac{k}{40}, x^2+y^2=\frac{k}{100}\). The level curves represent circles of radii \(\displaystyle \sqrt{10k}/20\) and \(\displaystyle \sqrt{k}/10\)
14.2: Limits and Continuity
For the following exercises, find the limit of the function.
1) \(\displaystyle \lim_{(x,y)→(1,2)}x\)6.2E: Exercises
2) \(\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}\)
Solution:\(\displaystyle 2.0\)
3) Show that the limit \(\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}\) exists and is the same along the paths: \(\displaystyle y-axis\) and \(\displaystyle x-axis\), and along \(\displaystyle y=x\).
For the following exercises, evaluate the limits at the indicated values of \(\displaystyle x\) and \(\displaystyle y\). If the limit does not exist, state this and explain why the limit does not exist.
4) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}\)
Solution:\(\displaystyle \frac{2}{3}\)
5) \(\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}\)
6) \(\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2sinx}{x}\)
Solution:\(\displaystyle 1\)
7) \(\displaystyle \lim_{(x,y)→(0,0)}sin(\frac{x^8+y^7}{x−y+10})\)
8) \(\displaystyle \lim_{(x,y)→(π/4,1)}\frac{ytanx}{y+1}\)
Solution:\(\displaystyle \frac{1}{2}\)
9) \(\displaystyle \lim_{(x,y)→(0,π/4)}\frac{secx+2}{3x−tany}\)
10) \(\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})\)
Solution:\(\displaystyle −\frac{1}{2}\)
11) \(\displaystyle \lim_{(x,y)→(4,4)}xlny\)
12) \(\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}\)
Solution:\(\displaystyle e^{−32}\)
13) \(\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}\)
14) \(\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)\)
Solution:\(\displaystyle 11.0\)
15) \(\displaystyle \lim_{(x,y)→(π,π)}xsin(\frac{x+y}{4})\)
16) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}\)
Solution:\(\displaystyle 1.0\)
17) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}\)
18) \(\displaystyle \lim_{(x,y)→(0,0)}ln(x^2+y^2)\)
Solution:The limit does not exist because when \(\displaystyle x\) and \(\displaystyle y\) both approach zero, the function approaches \(\displaystyle ln0\), which is undefined (approaches negative infinity).
For the following exercises, complete the statement.
19) A point \(\displaystyle (x_0,y_0)\) in a plane region \(\displaystyle R\) is an interior point of \(\displaystyle R\) if _________________.
20) A point \(\displaystyle (x_0,y_0)\) in a plane region R is called a boundary point of \(\displaystyle R\) if ___________.
Solution:every open disk centered at \(\displaystyle (x_0,y_0)\) contains points inside \(\displaystyle R\) and outside \(\displaystyle R\)
For the following exercises, use algebraic techniques to evaluate the limit.
21) \(\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}\)
22) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}\)
Solution:\(\displaystyle 0.0\)
23) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}\)
24) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}\)
Solution:\(\displaystyle 0.00\)
For the following exercises, evaluate the limits of the functions of three variables.
25) \(\displaystyle lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}\)
26) \(\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}\)
Solution:The limit does not exist.
For the following exercises, evaluate the limit of the function by determining the value the function approaches along the indicated paths. If the limit does not exist, explain why not.
27) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}\)
a. Along the \(\displaystyle x-axis\) \(\displaystyle (y=0)\)
b. Along the \(\displaystyle y-axis\) \(\displaystyle (x=0)\)
c. Along the path \(\displaystyle y=2x\)
28) Evaluate \(\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}\) using the results of previous problem.
Solution:The limit does not exist. The function approaches two different values along different paths.
29) \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}\)
a. Along the \(\displaystyle x-axis\) \(\displaystyle (y=0)\)
b. Along the \(\displaystyle y-axis\) \(\displaystyle (x=0)\)
c. Along the path \(\displaystyle y=x^2\)
30) Evaluate \(\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}\) using the results of previous problem.
Solution:The limit does not exist because the function approaches two different values along the paths.
Discuss the continuity of the following functions. Find the largest region in the \(\displaystyle xy-plane\) in which the following functions are continuous.
31) \(\displaystyle f(x,y)=sin(xy)\)
32) \(\displaystyle f(x,y)=ln(x+y)\)
Solution:The function \(\displaystyle f\) is continuous in the region \(\displaystyle y>−x.\)
33) \(\displaystyle f(x,y)=e^{3xy}\)
34) \(\displaystyle f(x,y)=\frac{1}{xy}\)
Solution:The function \(\displaystyle f\) is continuous at all points in the \(\displaystyle xy-plane\) except at \(\displaystyle (0,0).\)
For the following exercises, determine the region in which the function is continuous. Explain your answer.
35) \(\displaystyle f(x,y)=\frac{x^2y}{x^2+y^2}\)
36) \(\displaystyle f(x,y)=\)\(\displaystyle \begin{cases}\frac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}\)
(Hint: Show that the function approaches different values along two different paths.)
Solution:The function is continuous at \(\displaystyle (0,0)\) since the limit of the function at \(\displaystyle (0,0)\) is \(\displaystyle 0\), the same value of \(\displaystyle f(0,0).\)
37) \(\displaystyle f(x,y)=\frac{sin(x^2+y^2)}{x^2+y^2}\)
38) Determine whether \(\displaystyle g(x,y)=\frac{x^2−y^2}{x^2+y^2}\) is continuous at \(\displaystyle (0,0)\).
Solution:The function is discontinuous at \(\displaystyle (0,0).\) The limit at \(\displaystyle (0,0)\) fails to exist and \(\displaystyle g(0,0)\) does not exist.
39) Create a plot using graphing software to determine where the limit does not exist. Determine the region of the coordinate plane in which \(\displaystyle f(x,y)=\frac{1}{x^2−y}\) is continuous.
40) Determine the region of the \(\displaystyle xy-plane\) in which the composite function \(\displaystyle g(x,y)=arctan(\frac{xy^2}{x+y})\) is continuous. Use technology to support your conclusion.
Solution:Since the function \(\displaystyle arctanx\) is continuous over \(\displaystyle (−∞,∞), g(x,y)=arctan(\frac{xy^2}{x+y})\) is continuous where \(\displaystyle z=\frac{xy^2}{x+y}\) is continuous. The inner function \(\displaystyle z\) is continuous on all points of the \(\displaystyle xy-plane\) except where \(\displaystyle y=−x.\) Thus, \(\displaystyle g(x,y)=arctan(\frac{xy^2}{x+y})\) is continuous on all points of the coordinate plane except at points at which \(\displaystyle y=−x.\)
41) Determine the region of the \(\displaystyle xy-plane\) in which \(\displaystyle f(x,y)=ln(x^2+y^2−1)\) is continuous. Use technology to support your conclusion. (Hint: Choose the range of values for \(\displaystyle x\) and \(\displaystyle y\) carefully!)
42) At what points in space is \(\displaystyle g(x,y,z)=x^2+y^2−2z^2\) continuous?
Solution:All points \(\displaystyle P(x,y,z)\) in space
43) At what points in space is \(\displaystyle g(x,y,z)=\frac{1}{x^2+z^2−1}\) continuous?
44) Show that \(\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}\) does not exist at \(\displaystyle (0,0)\) by plotting the graph of the function.
Solution:The graph increases without bound as \(\displaystyle x\) and \(\displaystyle y\) both approach zero.
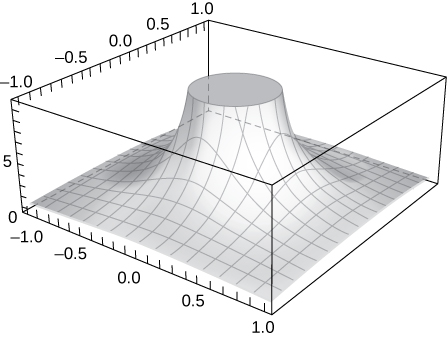
45) [T] Evaluate \(\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}\) by plotting the function using a CAS. Determine analytically the limit along the path \(\displaystyle x=y^2.\)
46) [T]
a. Use a CAS to draw a contour map of \(\displaystyle z=\sqrt{9−x^2−y^2}\).
b. What is the name of the geometric shape of the level curves?
c. Give the general equation of the level curves.
d. What is the maximum value of \(\displaystyle z\)?
e. What is the domain of the function?
f. What is the range of the function?
Solution:
a.
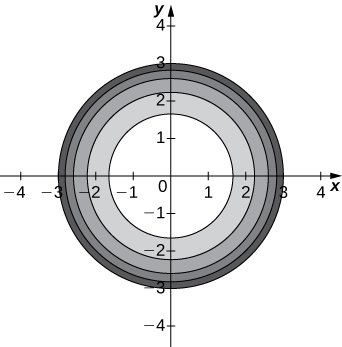
b. The level curves are circles centered at \(\displaystyle (0,0)\) with radius \(\displaystyle 9−c\). c. \(\displaystyle x^2+y^2=9−c\) d. \(\displaystyle z=3\) e. \(\displaystyle {(x,y)∈R^2∣x^2+y^2≤9}\) f. \(\displaystyle {z|0≤z≤3}\)
47) True or False: If we evaluate \(\displaystyle \lim_{(x,y)→(0,0)}f(x)\) along several paths and each time the limit is \(\displaystyle 1\), we can conclude that \(\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.\)
48) Use polar coordinates to find \(\displaystyle \lim_{(x,y)→(0,0)}\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.\) You can also find the limit using L’Hôpital’s rule.
Solution:\(\displaystyle 1.0\)
49) Use polar coordinates to find \(\displaystyle \lim_{(x,y)→(0,0)}cos(x^2+y^2).\)
50) Discuss the continuity of \(\displaystyle f(g(x,y))\) where \(\displaystyle f(t)=1/t\) and \(\displaystyle g(x,y)=2x−5y.\)
Solution:\(\displaystyle f(g(x,y))\) is continuous at all points \(\displaystyle (x,y)\) that are not on the line \(\displaystyle 2x−5y=0.\)
51) Given \(\displaystyle f(x,y)=x^2−4y,\) find \(\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.\)
52) Given \(\displaystyle f(x,y)=x^2−4y,\) find \(\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}\).
Solution:\(\displaystyle 2.0\)
14.3: Partial Derivatives
For the following exercises, calculate the partial derivative using the limit definitions only.
1) \(\displaystyle \frac{∂z}{∂x}\) for \(\displaystyle z=x^2−3xy+y^2\)
2) \(\displaystyle \frac{∂z}{∂y}\) for \(\displaystyle z=x^2−3xy+y^2\)
Solution:\(\displaystyle \frac{∂z}{∂y}=−3x+2y\)
For the following exercises, calculate the sign of the partial derivative using the graph of the surface.
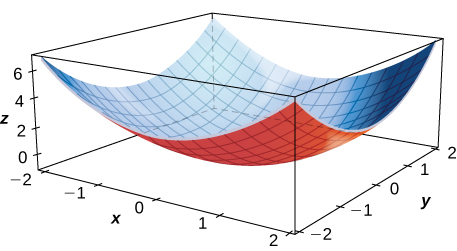
3) \(\displaystyle f_x(1,1)\)
4) \(\displaystyle f_x(−1,1)\)
Solution:The sign is negative.
5) \(\displaystyle f_y(1,1)\)
6) \(\displaystyle f_x(0,0)\)
Solution:The partial derivative is zero at the origin.
For the following exercises, calculate the partial derivatives.
7) \(\displaystyle \frac{∂z}{∂x}\) for \(\displaystyle z=sin(3x)cos(3y)\)
8) \(\displaystyle \frac{∂z}{∂y}\) for \(\displaystyle z=sin(3x)cos(3y)\)
Solution:\(\displaystyle \frac{∂z}{∂y}=−3sin(3x)sin(3y)\)
9) \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\) for \(\displaystyle z=x^8e^3y\)
10) \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\) for \(\displaystyle z=ln(x^6+y^4)\)
Solution:\(\displaystyle \frac{∂z}{∂x}=\frac{6x^5}{x^6+y^4};\frac{∂z}{∂y}=\frac{4y^3}{x^6+y^4}\)
11) Find \(\displaystyle f_y(x,y)\) for \(\displaystyle f(x,y)=e^{xy}cos(x)sin(y).\)
12) Let \(\displaystyle z=e^{xy}.\) Find \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\).
Solution:\(\displaystyle \frac{∂z}{∂x}=ye^{xy};\frac{∂z}{∂y}=xe^{xy}\)
13) Let \(\displaystyle z=ln(\frac{x}{y})\). Find \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\).
14) Let \(\displaystyle z=tan(2x−y).\) Find \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\).
Solution:\(\displaystyle \frac{∂z}{∂x}=2sec^2(2x−y),\frac{∂z}{∂y}=−sec^2(2x−y)\)
15) Let \(\displaystyle z=sinh(2x+3y).\) Find \(\displaystyle \frac{∂z}{∂x}\) and \(\displaystyle \frac{∂z}{∂y}\).
16) Let \(\displaystyle f(x,y)=arctan(\frac{y}{x}).\) Evaluate \(\displaystyle f_x(2,−2)\) and \(\displaystyle f_y(2,−2)\).
Solution:\(\displaystyle f_x(2,−2)=\frac{1}{4}=f_y(2,−2)\)
17) Let \(\displaystyle f(x,y)=\frac{xy}{x−y}.\) Find \(\displaystyle f_x(2,−2)\) and \(\displaystyle f_y(2,−2).\)
Evaluate the partial derivatives at point \(\displaystyle P(0,1).\)
18) Find \(\displaystyle \frac{∂z}{∂x}\) at \(\displaystyle (0,1)\) for \(\displaystyle z=e^{−x}cos(y)\).
Solution:\(\displaystyle \frac{∂z}{∂x}=−cos(1)\)
19) Given \(\displaystyle f(x,y,z)=x^3yz^2,\) find \(\displaystyle \frac{∂^2f}{∂x∂y}\) and \(\displaystyle f_z(1,1,1).\)
20) Given \(\displaystyle f(x,y,z)=2sin(x+y),\) find \(\displaystyle f_x(0,\frac{π}{2},−4), f_y(0,\frac{π}{2},−4),\) and \(\displaystyle f_z(0,\frac{π}{2},−4).\)
Solution:\(\displaystyle f_x=0,f_y=0,f_z=0\)
21) The area of a parallelogram with adjacent side lengths that are \(\displaystyle a\) and \(\displaystyle b\), and in which the angle between these two sides is \(\displaystyle θ\), is given by the function \(\displaystyle A(a,b,θ)=basin(θ).\)Find the rate of change of the area of the parallelogram with respect to the following:
a. Side a
b. Side b
c. \(\displaystyle Angleθ\)
22) Express the volume of a right circular cylinder as a function of two variables:
a. its radius \(\displaystyle r\) and its height \(\displaystyle h\).
b. Show that the rate of change of the volume of the cylinder with respect to its radius is the product of its circumference multiplied by its height.
c. Show that the rate of change of the volume of the cylinder with respect to its height is equal to the area of the circular base.
Solution:\(\displaystyle a. V(r,h)=πr^2h\) \(\displaystyle b. \frac{∂V}{∂r}=2πrh\) \(\displaystyle c. \frac{∂V}{∂h}=πr^2\)
23) Calculate \(\displaystyle \frac{∂w}{∂z}\) for \(\displaystyle w=zsin(xy^2+2z).\)
Find the indicated higher-order partial derivatives.
24) \(\displaystyle f_{xy}\) for \(\displaystyle z=ln(x−y)\)
Solution:\(\displaystyle f_{xy}=\frac{1}{(x−y)^2}\)
25) \(\displaystyle f_{yx}\) for \(\displaystyle z=ln(x−y)\)
26) Let \(\displaystyle z=x^2+3xy+2y^2.\) Find \(\displaystyle \frac{∂^2z}{∂x^2}\) and \(\displaystyle \frac{∂^2z}{∂y^2}\).
Solution:\(\displaystyle \frac{∂^2z}{∂x^2}=2,\frac{∂^2z}{∂y^2}=4\)
27) Given \(\displaystyle z=e^xtany,\) find \(\displaystyle \frac{∂^2z}{∂x∂y}\) and \(\displaystyle \frac{∂^2z}{∂y∂x}\).
28) Given \(\displaystyle f(x,y,z)=xyz,\) find \(\displaystyle f_{xyy},f_{yxy},\) and \(\displaystyle f_{yyx}\).
Solution:\(\displaystyle f_{xyy}=f_{yxy}=f_{yyx}=0\)
29) Given \(\displaystyle f(x,y,z)=e^{−2x}sin(z^2y),\) show that \(\displaystyle f_{xyy}=f_{yxy}\).
30) Show that \(\displaystyle z=\frac{1}{2}(e^y−e^{−y})sinx\) is a solution of the differential equation \(\displaystyle \frac{∂^2z}{∂x^2}+\frac{∂^2z}{∂y^2}=0.\)
Solution:
\(\displaystyle \frac{d^2z}{dx^2}=−\frac{1}{2}(e^y−e^{−y})sinx\)
\(\displaystyle \frac{d^2z}{dy^2}=\frac{1}{2}(e^y−e^{−y})sinx\)
\(\displaystyle \frac{d^2z}{dx^2}+\frac{d^2z}{dy^2}=0\)
31) Find \(\displaystyle f_{xx}(x,y)\) for \(\displaystyle f(x,y)=\frac{4x^2}{y}+\frac{y^2}{2x}.\)
32) Let \(\displaystyle f(x,y,z)=x^2y^3z−3xy^2z^3+5x^2z−y^3z.\) Find \(\displaystyle f_{xyz}.\)
Solution:\(\displaystyle f_{xyz}=6y^2x−18yz^2\)
33) Let \(\displaystyle F(x,y,z)=x^3yz^2−2x^2yz+3xz−2y^3z.\) Find \(\displaystyle F_{xyz}\).
34) Given \(\displaystyle f(x,y)=x^2+x−3xy+y^3−5,\) find all points at which \(\displaystyle f_x=f_y=0\) simultaneously.
Solution:\(\displaystyle (\frac{1}{4},\frac{1}{2}),(1,1)\)
35) Given \(\displaystyle f(x,y)=2x^2+2xy+y^2+2x−3,\) find all points at which \(\displaystyle \frac{∂f}{∂x}=0\) and \(\displaystyle \frac{∂f}{∂y}=0\) simultaneously.
36) Given \(\displaystyle f(x,y)=y^3−3yx^2−3y^2−3x^2+1\), find all points on \(\displaystyle f\) at which \(\displaystyle f_x=f_y=0\) simultaneously.
Solution:\(\displaystyle (0,0),(0,2),(\sqrt{3},−1),(−\sqrt{3},−1)\)
37) Given \(\displaystyle f(x,y)=15x^3−3xy+15y^3,\) find all points at which \(\displaystyle f_x(x,y)=f_y(x,y)=0\) simultaneously.
38) Show that \(\displaystyle z=e^xsiny\) satisfies the equation \(\displaystyle \frac{∂^2z}{∂x^2}+\frac{∂^2z}{∂y^2}=0.\)
Solution:\(\displaystyle \frac{∂^2z}{∂x^2}+\frac{∂^2z}{∂y^2}=e^xsin(y)−e^xsiny=0\)
39) Show that \(\displaystyle f(x,y)=ln(x^2+y^2)\) solves Laplace’s equation \(\displaystyle \frac{∂^2z}{∂x^2}+\frac{∂^2z}{∂y^2}=0.\)
40) Show that \(\displaystyle z=e^{−t}cos(\frac{x}{c})\) satisfies the heat equation \(\displaystyle \frac{∂z}{∂t}=−e^{−t}cos(\frac{x}{c}).\)
Solution:\(\displaystyle c^2\frac{∂^2z}{∂x^2}=e^{−t}cos(\frac{x}{c})\)
41) Find \(\displaystyle \lim_{Δx→0}\frac{f(x+Δx)−f(x,y)}{Δx}\) for \(\displaystyle f(x,y)=−7x−2xy+7y.\)
42) Find \(\displaystyle \lim_{Δy→0}\frac{f(x,y+Δy)−f(x,y)}{Δy}\) for \(\displaystyle f(x,y)=−7x−2xy+7y.\)
Solution:\(\displaystyle \frac{∂f}{∂y}=−2x+7\)
43) Find \(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) for \(\displaystyle f(x,y)=x^2y^2+xy+y.\)
44) Find \(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) for \(\displaystyle f(x,y)=sin(xy).\)
Solution:\(\displaystyle \frac{∂f}{∂x}=ycosxy\)
45) The function \(\displaystyle P(T,V)=\frac{nRT}{V}\) gives the pressure at a point in a gas as a function of temperature \(\displaystyle T\) and volume \(\displaystyle V\). The letters \(\displaystyle n\) and \(\displaystyle R\) are constants. Find \(\displaystyle \frac{∂P}{∂V}\) and \(\displaystyle \frac{∂P}{∂T}\), and explain what these quantities represent.
46) The equation for heat flow in the \(\displaystyle xy-plane\) is \(\displaystyle \frac{∂f}{∂t}=\frac{∂^2f}{∂x^2}+\frac{∂^2f}{∂y^2}\). Show that \(\displaystyle f(x,y,t)=e^{−2t}sinxsiny\) is a solution.
47) The basic wave equation is \(\displaystyle f_{tt}=f_{xx}.\) Verify that \(\displaystyle f(x,t)=sin(x+t)\) and \(\displaystyle f(x,t)=sin(x−t)\) are solutions.
48) The law of cosines can be thought of as a function of three variables. Let \(\displaystyle x,y,\) and \(\displaystyle θ\) be two sides of any triangle where the angle \(\displaystyle θ\) is the included angle between the two sides. Then, \(\displaystyle F(x,y,θ)=x^2+y^2−2xycosθ\) gives the square of the third side of the triangle. Find \(\displaystyle \frac{∂F}{∂θ}\) and \(\displaystyle \frac{∂F}{∂x}\) when \(\displaystyle x=2,y=3,\) and \(\displaystyle θ=\frac{π}{6}.\)
Solution:\(\displaystyle \frac{∂F}{∂θ}=6,\frac{∂F}{∂x}=4−3\sqrt{3}\)
49) Suppose the sides of a rectangle are changing with respect to time. The first side is changing at a rate of \(\displaystyle 2\)in./sec whereas the second side is changing at the rate of \(\displaystyle 4\) in/sec. How fast is the diagonal of the rectangle changing when the first side measures \(\displaystyle 16\) in. and the second side measures \(\displaystyle 20\) in.? (Round answer to three decimal places.)
50) A Cobb-Douglas production function is \(\displaystyle f(x,y)=200x^{0.7}y^{0.3},\) where \(\displaystyle x\) and \(\displaystyle y\) represent the amount of labor and capital available. Let \(\displaystyle x=500\) and \(\displaystyle y=1000.\) Find \(\displaystyle \frac{δf}{δx}\) and \(\displaystyle \frac{δf}{δy}\) at these values, which represent the marginal productivity of labor and capital, respectively.
Solution:\(\displaystyle \frac{δf}{δx}\) at \(\displaystyle (500,1000)=172.36, \frac{δf}{δy}\) at \(\displaystyle (500,1000)=36.93\)
51) The apparent temperature index is a measure of how the temperature feels, and it is based on two variables: \(\displaystyle h\), which is relative humidity, and \(\displaystyle t\), which is the air temperature.
\(\displaystyle A=0.885t−22.4h+1.20th−0.544.\) Find \(\displaystyle \frac{∂A}{∂t}\) and \(\displaystyle \frac{∂A}{∂h}\) when \(\displaystyle t=20°F\) and \(\displaystyle h=0.90.\)
14.4: Tangent Planes and Linear Approximations
For the following exercises, find a unit normal vector to the surface at the indicated point.
1) \(\displaystyle f(x,y)=x^3,(2,−1,8)\)
Solution:\(\displaystyle (\frac{\sqrt{145}}{145})(12i−k)\)
2) \(\displaystyle ln(\frac{x}{y−z})=0\) when \(\displaystyle x=y=1\)
For the following exercises, as a useful review for techniques used in this section, find a normal vector and a tangent vector at point \(\displaystyle P\).
3) \(\displaystyle x^2+xy+y^2=3,P(−1,−1)\)
Solution:Normal vector: \(\displaystyle i+j\), tangent vector: \(\displaystyle −j\)
4) \(\displaystyle (x^2+y^2)^2=9(x^2−y^2),d(\sqrt{2},1)\)
5) \(\displaystyle xy^2−2x^2+y+5x=6,P(4,2)\)
Solution:Normal vector: \(\displaystyle 7i−17j\), tangent vector: \(\displaystyle 7i+7j\)
6) \(\displaystyle 2x^3−x^2y^2=3x−y−7,P(1,−2)\)
7) \(\displaystyle ze^{x^2−y^2}−3=0, P(2,2,3)\)
Solution:\(\displaystyle −1.094i−0.18238j\)
For the following exercises, find the equation for the tangent plane to the surface at the indicated point. (Hint: Solve for \(\displaystyle z\) in terms of \(\displaystyle x\) and \(\displaystyle y\).)
8) \(\displaystyle −8x−3y−7z=−19,P(1,−1,2)\)
9) \(\displaystyle z=−9x^2−3y^2,P(2,1,−39)\)
Solution:\(\displaystyle −36x−6y−z=−39\)
10) \(\displaystyle x^2+10xyz+y^2+8z^2=0,P(−1,−1,−1)\)
11) \(\displaystyle z=ln(10x^2+2y^2+1),P(0,0,0)\)
Solution:\(\displaystyle z=0\)
12) \(\displaystyle z=e^{7x^2+4y^2}, P(0,0,1)\)
13) \(\displaystyle xy+yz+zx=11,P(1,2,3)\)
Solution:\(\displaystyle 5x+4y+3z−22=0\)
14) \(\displaystyle x^2+4y^2=z^2,P(3,2,5)\)
15) \(\displaystyle x^3+y^3=3xyz,P(1,2,\frac{3}{2})\)
Solution:\(\displaystyle 4x−5y+4z=0\)
16) \(\displaystyle z=axy,P(1,\frac{1}{a},1)\)
17) \(\displaystyle z=sinx+siny+sin(x+y),P(0,0,0)\)
Solution:\(\displaystyle 2x+2y−z=0\)
18) \(\displaystyle h(x,y)=ln\sqrt{x^2+y^2},P(3,4)\)
19) \(\displaystyle z=x^2−2xy+y^2,P(1,2,1)\)
Solution:\(\displaystyle −2(x−1)+2(y−2)−(z−1)=0\)
For the following exercises, find parametric equations for the normal line to the surface at the indicated point. (Recall that to find the equation of a line in space, you need a point on the line, \(\displaystyle P_0(x_0,y_0,z_0)\), and a vector \(\displaystyle n=⟨a,b,c⟩\) that is parallel to the line. Then the equation of the line is \(\displaystyle x−x_0=at,y−y_0=bt,z−z_0=ct.)\)
20) \(\displaystyle −3x+9y+4z=−4,P(1,−1,2)\)
21) \(\displaystyle z=5x^2−2y^2,P(2,1,18)\)
Solution:\(\displaystyle x=20t+2,y=−4t+1,z=−t+18\)
22) \(\displaystyle x^2−8xyz+y^2+6z^2=0,P(1,1,1)\)
23) \(\displaystyle z=ln(3x^2+7y^2+1),P(0,0,0)\)
Solution:\(\displaystyle x=0,y=0,z=t\)
24) \(\displaystyle z=e^{4x^2+6y^2},P(0,0,1)\)
25) \(\displaystyle z=x^2−2xy+y^2\) at point \(\displaystyle P(1,2,1)\)
Solution:\(\displaystyle x−1=2t;y−2=−2t;z−1=t\)
For the following exercises, use the figure shown here.
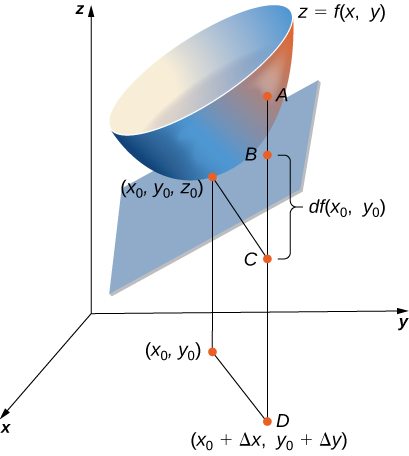
26) The length of line segment \(\displaystyle AC\) is equal to what mathematical expression?
27) The length of line segment \(\displaystyle BC\) is equal to what mathematical expression?
Solution:The differential of the function \(\displaystyle z(x,y)=dz=f_xdx+f_ydy\)
28) Using the figure, explain what the length of line segment \(\displaystyle AB\) represents.
For the following exercises, complete each task.
29) Show that \(\displaystyle f(x,y)=e^{xy}x\) is differentiable at point \(\displaystyle (1,0).\)
Solution:Using the definition of differentiability, we have \(\displaystyle e^{xy}x≈x+y.\)
30) Find the total differential of the function \(\displaystyle w=e^ycos(x)+z^2.\)
31) Show that \(\displaystyle f(x,y)=x^2+3y\) is differentiable at every point. In other words, show that \(\displaystyle Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy\), where both \(\displaystyle ε_1\) and \(\displaystyle ε_2\) approach zero as \(\displaystyle (Δx,Δy)\) approaches \(\displaystyle (0,0).\)
Solution:\(\displaystyle Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0\) for small \(\displaystyle Δx\) and \(\displaystyle z\) satisfies the definition of differentiability.
32) Find the total differential of the function \(\displaystyle z=\frac{xy}{y+x}\) where \(\displaystyle x\) changes from \(\displaystyle 10\) to \(\displaystyle 10.5\) and \(\displaystyle y\) changes from \(\displaystyle 15\) to \(\displaystyle 13\).
33) Let \(\displaystyle z=f(x,y)=xe^y.\) Compute \(\displaystyle Δz\) from \(\displaystyle P(1,2)\) to \(\displaystyle Q(1.05,2.1)\) and then find the approximate change in \(\displaystyle z\) from point \(\displaystyle P\) to point \(\displaystyle Q\). Recall \(\displaystyle Δz=f(x+Δx,y+Δy)−f(x,y)\), and \(\displaystyle dz\) and \(\displaystyle Δz\) are approximately equal.
Solution:\(\displaystyle Δz≈1.185422\) and \(\displaystyle dz≈1.108.\) They are relatively close.
34) The volume of a right circular cylinder is given by \(\displaystyle V(r,h)=πr^2h.\) Find the differential \(\displaystyle dV\). Interpret the formula geometrically.
35) See the preceding problem. Use differentials to estimate the amount of aluminum in an enclosed aluminum can with diameter \(\displaystyle 8.0cm\) and height \(\displaystyle 12cm\) if the aluminum is \(\displaystyle 0.04\) cm thick.
Solution:\(\displaystyle 16cm^3\)
36) Use the differential \(\displaystyle dz\) to approximate the change in \(\displaystyle z=\sqrt{4−x^2−y^2}\) as \(\displaystyle (x,y)\) moves from point \(\displaystyle (1,1)\) to point \(\displaystyle (1.01,0.97).\) Compare this approximation with the actual change in the function.
37) Let \(\displaystyle z=f(x,y)=x^2+3xy−y^2.\) Find the exact change in the function and the approximate change in the function as \(\displaystyle x\) changes from \(\displaystyle 2.00\) to \(\displaystyle 92.05\) and \(\displaystyle y\) changes from \(\displaystyle 3.00\) to \(\displaystyle 2.96\).
Solution:\(\displaystyle Δz=\) exact change \(\displaystyle =0.6449\), approximate change is \(\displaystyle dz=0.65\). The two values are close.
38) The centripetal acceleration of a particle moving in a circle is given by \(\displaystyle a(r,v)=\frac{v^2}{r},\) where \(\displaystyle v\) is the velocity and \(\displaystyle r\) is the radius of the circle. Approximate the maximum percent error in measuring the acceleration resulting from errors of \(\displaystyle 3%\) in \(\displaystyle v\) and \(\displaystyle 2%\) in \(\displaystyle r\). (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in a is given by \(\displaystyle \frac{da}{a}\).)
39) The radius \(\displaystyle r\) and height \(\displaystyle h\) of a right circular cylinder are measured with possible errors of \(\displaystyle 4%\) and \(\displaystyle 5%\), respectively. Approximate the maximum possible percentage error in measuring the volume (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in \(\displaystyle V\) is given by \(\displaystyle \frac{dV}{V}\).)
Solution:\(\displaystyle 13%\) or \(\displaystyle 0.13\)
40) The base radius and height of a right circular cone are measured as \(\displaystyle 10\) in. and \(\displaystyle 25\) in., respectively, with a possible error in measurement of as much as \(\displaystyle 0.1\) in. each. Use differentials to estimate the maximum error in the calculated volume of the cone.
41) The electrical resistance \(\displaystyle R\) produced by wiring resistors \(\displaystyle R_1\) and \(\displaystyle R_2\) in parallel can be calculated from the formula \(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\). If \(\displaystyle R_1\) and \(\displaystyle R_2\) are measured to be \(\displaystyle 7Ω\) and \(\displaystyle 6Ω\), respectively, and if these measurements are accurate to within \(\displaystyle 0.05Ω\), estimate the maximum possible error in computing \(\displaystyle R\). (The symbol \(\displaystyle Ω\) represents an ohm, the unit of electrical resistance.)
Solution:\(\displaystyle 0.025\)
42) The area of an ellipse with axes of length \(\displaystyle 2a\) and \(\displaystyle 2b\) is given by the formula \(\displaystyle A=πab\). Approximate the percent change in the area when \(\displaystyle a\) increases by \(\displaystyle 2%\) and \(\displaystyle b\) increases by \(\displaystyle 1.5%.\)
43) The period \(\displaystyle T\) of a simple pendulum with small oscillations is calculated from the formula \(\displaystyle T=2π\sqrt{\frac{L}{g}}\), where \(\displaystyle L\) is the length of the pendulum and \(\displaystyle g\) is the acceleration resulting from gravity. Suppose that \(\displaystyle L\) and \(\displaystyle g\) have errors of, at most, \(\displaystyle 0.5%\) and \(\displaystyle 0.1%\), respectively. Use differentials to approximate the maximum percentage error in the calculated value of \(\displaystyle T\).
Solution:\(\displaystyle 0.3%\)
44) Electrical power \(\displaystyle P\) is given by \(\displaystyle P=\frac{V^2}{R}\), where \(\displaystyle V\) is the voltage and \(\displaystyle R\) is the resistance. Approximate the maximum percentage error in calculating power if \(\displaystyle 120 V\) is applied to a \(\displaystyle 2000−Ω\) resistor and the possible percent errors in measuring \(\displaystyle V\) and \(\displaystyle R\) are \(\displaystyle 3%\) and \(\displaystyle 4%\), respectively.
For the following exercises, find the linear approximation of each function at the indicated point.
45) \(\displaystyle f(x,y)=x\sqrt{y},P(1,4)\)
Solution:\(\displaystyle 2x+\frac{1}{4}y−1\)
46) \(\displaystyle f(x,y)=e^xcosy;P(0,0)\)
47) \(\displaystyle f(x,y)=arctan(x+2y),P(1,0)\)
Solution:\(\displaystyle \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}\)
48) \(\displaystyle f(x,y)=\sqrt{20−x^2−7y^2},P(2,1)\)
49) \(\displaystyle f(x,y,z)=\sqrt{x^2+y^2+z^2},P(3,2,6)\)
Solution:\(\displaystyle \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z\)
50) [T] Find the equation of the tangent plane to the surface \(\displaystyle f(x,y)=x^2+y^2\) at point \(\displaystyle (1,2,5),\) and graph the surface and the tangent plane at the point.
51) [T] Find the equation for the tangent plane to the surface at the indicated point, and graph the surface and the tangent plane: \(\displaystyle z=ln(10x^2+2y^2+1),P(0,0,0).\)
Solution:\(\displaystyle z=0\)
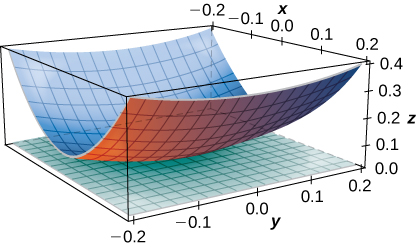
52) [T] Find the equation of the tangent plane to the surface \(\displaystyle z=f(x,y)=sin(x+y^2)\) at point \(\displaystyle (\frac{π}{4},0,\frac{\sqrt{2}}{2})\), and graph the surface and the tangent plane.
14.5: The Chain Rule
For the following exercises, use the information provided to solve the problem.
1) Let \(\displaystyle w(x,y,z)=xycosz,\) where \(\displaystyle x=t,y=t^2,\) and \(\displaystyle z=arcsint.\) Find \(\displaystyle \frac{dw}{dt}\).
Solution:\(\displaystyle \frac{dw}{dt}=ycosz+xcosz(2t)−\frac{xysinz}{\sqrt{1−t^2}}\)
2) Let \(\displaystyle w(t,v)=e^{tv}\) where \(\displaystyle t=r+s\) and \(\displaystyle v=rs\). Find \(\displaystyle \frac{∂w}{∂r}\) and \(\displaystyle \frac{∂w}{∂s}\).
3) If \(\displaystyle w=5x^2+2y^2,x=−3s+t,\) and \(\displaystyle y=s−4t,\) find \(\displaystyle \frac{∂w}{∂s}\) and \(\displaystyle \frac{∂w}{∂t}\).
Solution:\(\displaystyle \frac{∂w}{∂s}=−30x+4y, \frac{∂w}{∂t}=10x−16y\)
4) If \(\displaystyle w=xy^2,x=5cos(2t),\) and \(\displaystyle y=5sin(2t)\), find \(\displaystyle \frac{∂w}{∂t}\).
5) If \(\displaystyle f(x,y)=xy,x=rcosθ,\) and \(\displaystyle y=rsinθ\), find ∂f∂r and express the answer in terms of \(\displaystyle r\) and \(\displaystyle θ\).
Solution:\(\displaystyle \frac{∂f}{∂r}=rsin(2θ)\)
6) Suppose \(\displaystyle f(x,y)=x+y,u=e^xsiny,x=t^2\) and \(\displaystyle y=πt\), where \(\displaystyle x=rcosθ\) and \(\displaystyle y=rsinθ\). Find \(\displaystyle \frac{∂f}{∂θ}\).
For the following exercises, find \(\displaystyle \frac{df}{dt}\) using the chain rule and direct substitution.
7) \(\displaystyle f(x,y)=x^2+y^2, x=t,y=t^2\)
Solution:\(\displaystyle \frac{df}{dt}=2t+4t^3\)
8) \(\displaystyle f(x,y)=\sqrt{x^2+y^2},y=t^2,x=t\)
9) \(\displaystyle f(x,y)=xy,x=1−\sqrt{t},y=1+\sqrt{t}\)
Solution:\(\displaystyle \frac{df}{dt}=−1\)
10) \(\displaystyle f(x,y)=\frac{x}{y},x=e^t,y=2e^t\)
11) \(\displaystyle f(x,y)=ln(x+y), x=e^t,y=e^t\)
Solution:\(\displaystyle \frac{df}{dt}=1\)
12) \(\displaystyle f(x,y)=x^4, x=t,y=t\)
13) Let \(\displaystyle w(x,y,z)=x^2+y^2+z^2, x=cost,y=sint,\) and \(\displaystyle z=e^t\). Express \(\displaystyle w\) as a function of \(\displaystyle t\) and find \(\displaystyle \frac{dw}{dt}\) directly. Then, find \(\displaystyle \frac{dw}{dt}\) using the chain rule.
Solution:\(\displaystyle \frac{dw}{dt}=2e^{2t}\) in both cases
14) Let \(\displaystyle z=x^2y,\) where \(\displaystyle x=t^2\) and \(\displaystyle y=t^3\). Find \(\displaystyle \frac{dz}{dt}\).
15) Let \(\displaystyle u=e^xsiny,\) where \(\displaystyle x=t^2\) and \(\displaystyle y=πt\). Find \(\displaystyle \frac{du}{dt}\) when \(\displaystyle x=ln2\) and \(\displaystyle y=\frac{π}{4}\).
Solution:\(\displaystyle 2\sqrt{2}t+\sqrt{2}π=\frac{du}{dt}\)
For the following exercises, find \(\displaystyle \frac{dy}{dx}\)using partial derivatives.
16) \(\displaystyle sin(6x)+tan(8y)+5=0\)
17) \(\displaystyle x^3+y^2x−3=0\)
Solution:\(\displaystyle \frac{dy}{dx}=−\frac{3x^2+y^2}{2xy}\)
18) \(\displaystyle sin(x+y)+cos(x−y)=4\)
19) \(\displaystyle x^2−2xy+y^4=4\)
Solution:\(\displaystyle \frac{dy}{dx}=\frac{y−x}{−x+2y^3}\)
20) \(\displaystyle xe^y+ye^x−2x^2y=0\)
21) \(\displaystyle x^{2/3}+y^{2/3}=a^{2/3}\)
Solution:\(\displaystyle \frac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}\)
22) \(\displaystyle xcos(xy)+ycosx=2\)
23) \(\displaystyle e^{xy}+ye^y=1\)
Solution:\(\displaystyle \frac{dy}{dx}=−\frac{ye^{xy}}{xe^{xy}+e^y(1+y)}\)
24) \(\displaystyle x^2y^3+cosy=0\)
25) Find \(\displaystyle \frac{dz}{dt}\) using the chain rule where \(\displaystyle z=3x^2y^3,x=t^4,\) and \(\displaystyle y=t^2\).
Solution:\(\displaystyle \frac{dz}{dt}=42t^{13}\)
26) Let \(\displaystyle z=3cosx−sin(xy),x=\frac{1}{t},\) and \(\displaystyle y=3t.\) Find \(\displaystyle \frac{dz}{dt}\).
27) Let \(\displaystyle z=e^{1−xy},x=t^{1/3},\) and \(\displaystyle y=t^3\). Find \(\displaystyle \frac{dz}{dt}\).
Solution:\(\displaystyle \frac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}\)
28) Find \(\displaystyle \frac{dz}{dt}\) by the chain rule where \(\displaystyle z=cosh^2(xy),x=\frac{1}{2}t,\) and \(\displaystyle y=e^t\).
29) Let \(\displaystyle z=\frac{x}{y},x=2cosu,\) and \(\displaystyle y=3sinv.\) Find \(\displaystyle \frac{∂z}{∂u}\) and \(\displaystyle \frac{∂z}{∂v}\).
Solution:\(\displaystyle \frac{∂z}{∂u}=\frac{−2sinu3}{sinv}\) and \(\displaystyle \frac{∂z}{∂v}=\frac{−2cosucosv3}{sin^2v}\)
30) Let \(\displaystyle z=e^{x^2y}\), where \(\displaystyle x=\sqrt{uv}\) and \(\displaystyle y=\frac{1}{v}\). Find \(\displaystyle \frac{∂z}{∂u}\) and \(\displaystyle \frac{∂z}{∂v}\).
31) If \(\displaystyle z=xye^{x/y}, x=rcosθ,\) and \(\displaystyle y=rsinθ\), find \(\displaystyle \frac{∂z}{∂r}\) and \(\displaystyle \frac{∂z}{∂θ}\) when \(\displaystyle r=2\) and \(\displaystyle θ=\frac{π}{6}\).
Solution:\(\displaystyle \frac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \frac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}\)
32) Find \(\displaystyle \frac{∂w}{∂s}\) if \(\displaystyle w=4x+y^2+z^3,x=e^{rs^2},y=ln(\frac{r+s}{t}),\) and \(\displaystyle z=rst^2\).
33) If \(\displaystyle w=sin(xyz),x=1−3t,y=e^{1−t},\) and \(\displaystyle z=4t\), find \(\displaystyle \frac{∂w}{∂t}\).
Solution:\(\displaystyle \frac{∂w}{∂t}=cos(xyz)×yz×(−3)−cos(xyz)xze^{1−t}+cos(xyz)xy×4\)
For the following exercises, use this information: A function \(\displaystyle f(x,y)\) is said to be homogeneous of degree \(\displaystyle n\) if \(\displaystyle f(tx,ty)=t^nf(x,y)\). For all homogeneous functions of degree \(\displaystyle n\), the following equation is true: \(\displaystyle x\frac{∂f}{∂x}+y\frac{∂f}{∂y}=nf(x,y)\). Show that the given function is homogeneous and verify that \(\displaystyle x\frac{∂f}{∂x}+y\frac{∂f}{∂y}=nf(x,y)\).
34) \(\displaystyle f(x,y)=3x^2+y^2\)
35) \(\displaystyle f(x,y)=\sqrt{x^2+y^2}\)
Solution:\(\displaystyle f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \frac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)\)
36) \(\displaystyle f(x,y)=x^2y−2y^3\)
37) The volume of a right circular cylinder is given by \(\displaystyle V(x,y)=πx^2y,\) where \(\displaystyle x\) is the radius of the cylinder and \(\displaystyle y\) is the cylinder height. Suppose \(\displaystyle x\) and \(\displaystyle y\) are functions of \(\displaystyle t\) given by \(\displaystyle x=\frac{1}{2}t\) and \(\displaystyle y=\frac{1}{3}t\) so that \(\displaystyle x\) and \(\displaystyle y\) are both increasing with time. How fast is the volume increasing when \(\displaystyle x=2\) and \(\displaystyle y=5\)?
Solution:\(\displaystyle \frac{34π}{3}\)
38) The pressure \(\displaystyle P\) of a gas is related to the volume and temperature by the formula \(\displaystyle PV=kT\), where temperature is expressed in kelvins. Express the pressure of the gas as a function of both \(\displaystyle V\) and \(\displaystyle T\). Find \(\displaystyle \frac{dP}{dt}\) when \(\displaystyle k=1, \frac{dV}{dt}=2\) cm3/min, \(\displaystyle \frac{dT}{dt}=12\) K/min, \(\displaystyle V=20 cm^3\), and \(\displaystyle T=20°F\).
39) The radius of a right circular cone is increasing at \(\displaystyle 3\) cm/min whereas the height of the cone is decreasing at \(\displaystyle 2\) cm/min. Find the rate of change of the volume of the cone when the radius is \(\displaystyle 13\) cm and the height is \(\displaystyle 18\) cm.
Solution:\(\displaystyle \frac{dV}{dt}=\frac{1066π}{3}cm^3/min\)
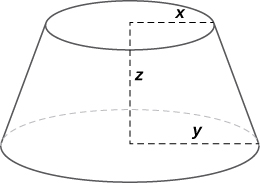
40) The volume of a frustum of a cone is given by the formula \(\displaystyle V=\frac{1}{3}πz(x^2+y^2+xy),\) where \(\displaystyle x\) is the radius of the smaller circle, \(\displaystyle y\) is the radius of the larger circle, and \(\displaystyle z\) is the height of the frustum (see figure). Find the rate of change of the volume of this frustum when \(\displaystyle x=10in.,y=12in.,\) and \(\displaystyle z=18in.\)
41) A closed box is in the shape of a rectangular solid with dimensions \(\displaystyle x,y,\) and \(\displaystyle z\). (Dimensions are in inches.) Suppose each dimension is changing at the rate of \(\displaystyle 0.5\) in./min. Find the rate of change of the total surface area of the box when \(\displaystyle x=2in.,y=3in.,\) and \(\displaystyle z=1in.\)
Solution:\(\displaystyle \frac{dA}{dt}=12in.^2/min\)
42) The total resistance in a circuit that has three individual resistances represented by \(\displaystyle x,y,\) and \(\displaystyle z\) is given by the formula \(\displaystyle R(x,y,z)=\frac{xyz}{yz+xz+xy}\). Suppose at a given time the \(\displaystyle x\) resistance is \(\displaystyle 100Ω\), the \(\displaystyle y\) resistance is \(\displaystyle 200Ω,\) and the \(\displaystyle z\) resistance is \(\displaystyle 300Ω.\) Also, suppose the \(\displaystyle x\) resistance is changing at a rate of \(\displaystyle 2Ω/min,\) the \(\displaystyle y\) resistance is changing at the rate of \(\displaystyle 1Ω/min\), and the \(\displaystyle z\) resistance has no change. Find the rate of change of the total resistance in this circuit at this time.
43) The temperature \(\displaystyle T\) at a point \(\displaystyle (x,y)\) is \(\displaystyle T(x,y)\) and is measured using the Celsius scale. A fly crawls so that its position after \(\displaystyle t\) seconds is given by \(\displaystyle x=\sqrt{1+t}\) and \(\displaystyle y=2+\frac{1}{3}t\), where \(\displaystyle x\) and \(\displaystyle y\) are measured in centimeters. The temperature function satisfies \(\displaystyle T_x(2,3)=4\) and \(\displaystyle T_y(2,3)=3\). How fast is the temperature increasing on the fly’s path after \(\displaystyle 3\) sec?
Solution:\(\displaystyle 2°C/sec\)
44) The \(\displaystyle x\) and \(\displaystyle y\) components of a fluid moving in two dimensions are given by the following functions: \(\displaystyle u(x,y)=2y\) and \(\displaystyle v(x,y)=−2x; x≥0;y≥0.\) The speed of the fluid at the point \(\displaystyle (x,y)\) is \(\displaystyle s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}\). Find \(\displaystyle \frac{∂s}{∂x}\) and \(\displaystyle \frac{∂s}{∂y}\) using the chain rule.
45) Let \(\displaystyle u=u(x,y,z),\) where \(\displaystyle x=x(w,t),y=y(w,t),z=z(w,t),w=w(r,s),\) and \(\displaystyle t=t(r,s).\) Use a tree diagram and the chain rule to find an expression for \(\displaystyle \frac{∂u}{∂r}\).
Solution:
\(\displaystyle \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})\)
14.6: Directional Derivatives and the Gradient
For the following exercises, find the directional derivative using the limit definition only.
1) \(\displaystyle f(x,y)=5−2x^2−\frac{1}{2}y^2\) at point \(\displaystyle P(3,4)\) in the direction of \(\displaystyle u=(cos\frac{π}{4})i+(sin\frac{π}{4})j\)
2) \(\displaystyle f(x,y)=y^2cos(2x)\) at point \(\displaystyle P(\frac{π}{3},2)\) in the direction of \(\displaystyle u=(cos\frac{π}{4})i+(sin\frac{π}{4})j\)
Solution:\(\displaystyle −3\sqrt{3}\)
3) Find the directional derivative of \(\displaystyle f(x,y)=y^2sin(2x)\) at point \(\displaystyle P(\frac{π}{4},2)\) in the direction of \(\displaystyle u=5i+12j.\)
For the following exercises, find the directional derivative of the function at point P in the direction of v.
4) \(\displaystyle f(x,y)=xy, P(0,−2), v=\frac{1}{2}i+\frac{\sqrt{3}}{2}j\)
Solution:\(\displaystyle −1\)
5) \(\displaystyle h(x,y)=e^xsiny,P(1,\frac{π}{2}),v=−i\)
6) \(\displaystyle h(x,y,z)=xyz,P(2,1,1),v=2i+j−k\)
Solution:\(\displaystyle \frac{2}{\sqrt{6}}\)
7) \(\displaystyle f(x,y)=xy,P(1,1),u=⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\)
8) \(\displaystyle f(x,y)=x^2−y^2,u=⟨\frac{\sqrt{3}}{2},\frac{1}{2}⟩,P(1,0)\)
Solution:\(\displaystyle \sqrt{3}\)
9) \(\displaystyle f(x,y)=3x+4y+7,u=⟨\frac{3}{5},\frac{4}{5}⟩,P(0,\frac{π}{2})\)
10) \(\displaystyle f(x,y)=e^xcosy,u=⟨0,1⟩,P=(0,\frac{π}{2})\)
Solution:\(\displaystyle −1.0\)
11) \(\displaystyle f(x,y)=y^{10},u=⟨0,−1⟩,P=(1,−1)\)
12) \(\displaystyle f(x,y)=ln(x^2+y^2),u=⟨\frac{3}{5},\frac{4}{5}⟩,P(1,2)\)
Solution:\(\displaystyle \frac{22}{25}\)
13) \(\displaystyle f(x,y)=x^2y,P(−5,5),v=3i−4j\)
14) \(\displaystyle f(x,y)=y^2+xz,P(1,2,2),v=⟨2,−1,2⟩\)
Solution:\(\displaystyle \frac{2}{3}\)
For the following exercises, find the directional derivative of the function in the direction of the unit vector \(\displaystyle u=cosθi+sinθj.\)
15) \(\displaystyle f(x,y)=x^2+2y^2,θ=\frac{π}{6}\)
16) \(\displaystyle f(x,y)=\frac{y}{x+2y},θ=−\frac{π}{4}\)
Solution:\(\displaystyle \frac{−\sqrt{2}(x+y)}{2(x+2y)^2}\)
17) \(\displaystyle f(x,y)=cos(3x+y),θ=\frac{π}{4}\)
18) \(\displaystyle w(x,y)=ye^x,θ=\frac{π}{3}\)
Solution:\(\displaystyle \frac{e^x(y+\sqrt{3})}{2}\)
19) \(\displaystyle f(x,y)=xarctan(y),θ=\frac{π}{2}\)
20) \(\displaystyle f(x,y)=ln(x+2y),θ=\frac{π}{3}\)
Solution:\(\displaystyle \frac{1+2\sqrt{3}}{2(x+2y)}\)
For the following exercises, find the gradient.
21) Find the gradient of \(\displaystyle f(x,y)=\frac{14−x^2−y^2}{3}\). Then, find the gradient at point \(\displaystyle P(1,2).\)
22) Find the gradient of \(\displaystyle f(x,y,z)=xy+yz+xz\) at point \(\displaystyle P(1,2,3).\)
Solution:\(\displaystyle ⟨5,4,3⟩\)
23) Find the gradient of \(\displaystyle f(x,y,z))\) at \(\displaystyle P\) and in the direction of \(\displaystyle u: f(x,y,z)=ln(x^2+2y^2+3z^2),P(2,1,4),u=\frac{−3}{13}i−\frac{4}{13}j−\frac{12}{13}k.\)
24) \(\displaystyle f(x,y,z)=4x^5y^2z^3,P(2,−1,1),u=\frac{1}{3}i+\frac{2}{3}j−\frac{2}{3}k\)
Solution:\(\displaystyle −320\)
For the following exercises, find the directional derivative of the function at point \(\displaystyle P\) in the direction of \(\displaystyle Q\).
25) \(\displaystyle f(x,y)=x^2+3y^2,P(1,1),Q(4,5)\)
26) \(\displaystyle f(x,y,z)=\frac{y}{x+z},P(2,1,−1),Q(−1,2,0)\)
Solution:\(\displaystyle \frac{3}{\sqrt{11}}\)
For the following exercises, find the derivative of the function at \(\displaystyle P\) in the direction of \(\displaystyle u\).
27) \(\displaystyle f(x,y)=−7x+2y,P(2,−4),u=4i−3j\)
28) \(\displaystyle f(x,y)=ln(5x+4y),P(3,9),u=6i+8j\)
Solution:\(\displaystyle \frac{31}{255}\)
29) [T] Use technology to sketch the level curve of \(\displaystyle f(x,y)=4x−2y+3\) that passes through \(\displaystyle P(1,2)\) and draw the gradient vector at \(\displaystyle P\).
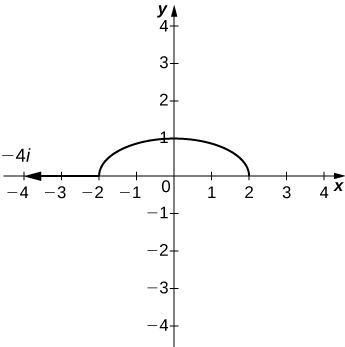
30) [T] Use technology to sketch the level curve of \(\displaystyle f(x,y)=x^2+4y^2\) that passes through \(\displaystyle P(−2,0)\) and draw the gradient vector at P.
Solution:
For the following exercises, find the gradient vector at the indicated point.
31) \(\displaystyle f(x,y)=xy^2−yx^2,P(−1,1)\)
32) \(\displaystyle f(x,y)=xe^y−ln(x),P(−3,0)\)
Solution:\(\displaystyle \frac{4}{3}i−3j\)
33) \(\displaystyle f(x,y,z)=xy−ln(z),P(2,−2,2)\)
34) \(\displaystyle f(x,y,z)=x\sqrt{y^2+z^2}, P(−2,−1,−1)\)
Solution:\(\displaystyle \sqrt{2}i+\sqrt{2}j+\sqrt{2}k\)
For the following exercises, find the derivative of the function.
35) \(\displaystyle f(x,y)=x^2+xy+y^2\) at point \(\displaystyle (−5,−4)\) in the direction the function increases most rapidly
36) \(\displaystyle f(x,y)=e^{xy}\) at point \(\displaystyle (6,7)\) in the direction the function increases most rapidly
Solution:\(\displaystyle 1.6(10^{19})\)
37) \(\displaystyle f(x,y)=arctan(\frac{y}{x})\) at point \(\displaystyle (−9,9)\) in the direction the function increases most rapidly
38) \(\displaystyle f(x,y,z)=ln(xy+yz+zx)\) at point \(\displaystyle (−9,−18,−27)\) in the direction the function increases most rapidly
Solution:\(\displaystyle \frac{5\sqrt{2}}{99}\)
39) \(\displaystyle f(x,y,z)=\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\) at point \(\displaystyle (5,−5,5)\) in the direction the function increases most rapidly
For the following exercises, find the maximum rate of change of \(\displaystyle f\) at the given point and the direction in which it occurs.
40) \(\displaystyle f(x,y)=xe^{−y}, (-2,0)\)
Solution:\(\displaystyle \sqrt{5},⟨1,2⟩\)
41) \(\displaystyle f(x,y)=\sqrt{x^2+2y}, (4,10)\)
42) \(\displaystyle f(x,y)=cos(3x+2y),(\frac{π}{6},−\frac{π}{8})\)
Solution:\(\displaystyle \sqrt{\frac{13}{2}},⟨−3,−2⟩\)
For the following exercises, find equations of
a. the tangent plane and
b. the normal line to the given surface at the given point.
43) The level curve \(\displaystyle f(x,y,z)=12\) for \(\displaystyle f(x,y,z)=4x^2−2y^2+z^2\) at point \(\displaystyle (2,2,2).\)
44) \(\displaystyle f(x,y,z)=xy+yz+xz=3\) at point \(\displaystyle (1,1,1)\)
Solution:\(\displaystyle a. x+y+z=3, b. x−1=y−1=z−1\)
45) \(\displaystyle f(x,y,z)=xyz=6\) at point \(\displaystyle (1,2,3)\)
46) \(\displaystyle f(x,y,z)=xe^ycosz−z=1\) at point \(\displaystyle (1,0,0)\)
Solution:\(\displaystyle a. x+y−z=1, b. x−1=y=−z\)
For the following exercises, solve the problem.
47) The temperature \(\displaystyle T\) in a metal sphere is inversely proportional to the distance from the center of the sphere (the origin: \(\displaystyle (0,0,0))\). The temperature at point \(\displaystyle (1,2,2)\) is \(\displaystyle 120°C.\)
a. Find the rate of change of the temperature at point \(\displaystyle (1,2,2)\) in the direction toward point \(\displaystyle (2,1,3).\)
b. Show that, at any point in the sphere, the direction of greatest increase in temperature is given by a vector that points toward the origin.
48) The electrical potential (voltage) in a certain region of space is given by the function \(\displaystyle V(x,y,z)=5x^2−3xy+xyz.\)
a. Find the rate of change of the voltage at point \(\displaystyle (3,4,5)\) in the direction of the vector \(\displaystyle ⟨1,1,−1⟩.\)
b. In which direction does the voltage change most rapidly at point \(\displaystyle (3,4,5)\)?
c. What is the maximum rate of change of the voltage at point \(\displaystyle (3,4,5)\)?
Solution:\(\displaystyle a. \frac{32}{\sqrt{3}}, b. ⟨38,6,12⟩, c. 2\sqrt{406}\)
49) If the electric potential at a point \(\displaystyle (x,y)\) in the xy-plane is \(\displaystyle V(x,y)=e^{−2x}cos(2y)\), then the electric intensity vector at \(\displaystyle (x,y)\) is \(\displaystyle E=−∇V(x,y).\)
a. Find the electric intensity vector at \(\displaystyle (\frac{π}{4},0).\)
b. Show that, at each point in the plane, the electric potential decreases most rapidly in the direction of the vector \(\displaystyle E.\)
50) In two dimensions, the motion of an ideal fluid is governed by a velocity potential \(\displaystyle φ\). The velocity components of the fluid u in the x-direction and v in the y-direction, are given by \(\displaystyle ⟨u,v⟩=∇φ\). Find the velocity components associated with the velocity potential \(\displaystyle φ(x,y)=sinπxsin2πy.\)
Solution:\(\displaystyle ⟨u,v⟩=⟨πcos(πx)sin(2πy),2πsin(πx)cos(2πy)⟩\)
14.7: Maxima/Minima Problems
For the following exercises, find all critical points.
1) \(\displaystyle f(x,y)=1+x^2+y^2\)
2) \(\displaystyle f(x,y)=(3x−2)^2+(y−4)^2\)
Solution:\(\displaystyle (\frac{2}{3},4)\)
3) \(\displaystyle f(x,y)=x^4+y^4−16xy\)
4) \(\displaystyle f(x,y)=15x^3−3xy+15y^3\)
Solution:\(\displaystyle (0,0) (\frac{1}{15},\frac{1}{15})\)
For the following exercises, find the critical points of the function by using algebraic techniques (completing the square) or by examining the form of the equation. Verify your results using the partial derivatives test.
5) \(\displaystyle f(x,y)=\sqrt{x^2+y^2+1}\)
6) \(\displaystyle f(x,y)=−x^2−5y^2+8x−10y−13\)
Solution:Maximum at \(\displaystyle (4,−1,8)\)
7) \(\displaystyle f(x,y)=x^2+y^2+2x−6y+6\)
8) \(\displaystyle f(x,y)=\sqrt{x^2+y^2}+1\)
Solution:Relative minimum at \(\displaystyle (0,0,1)\)
For the following exercises, use the second derivative test to identify any critical points and determine whether each critical point is a maximum, minimum, saddle point, or none of these.
9) \(\displaystyle f(x,y)=−x^3+4xy−2y^2+1\)
10) \(\displaystyle f(x,y)=x^2y^2\)
Solution:The second derivative test fails. Since \(\displaystyle x^2y^2>0\) for all \(\displaystyle x\) and \(\displaystyle y\) different from zero, and \(\displaystyle x^2y^2=0\) when either \(\displaystyle x\) or \(\displaystyle y\) equals zero (or both), then the absolute minimum occurs at \(\displaystyle (0,0).\)
11) \(\displaystyle f(x,y)=x^2−6x+y^2+4y−8\)
12) \(\displaystyle f(x,y)=2xy+3x+4y\)
Solution:\(\displaystyle f(−2,−\frac{3}{2})=−6\) is a saddle point.
13) \(\displaystyle f(x,y)=8xy(x+y)+7\)
14) \(\displaystyle f(x,y)=x^2+4xy+y^2\)
Solution:\(\displaystyle f(0,0)=0; (0,0,0)\) is a saddle point.
15) \(\displaystyle f(x,y)=x^3+y^3−300x−75y−3\)
16) \(\displaystyle f(x,y)=9−x^4y^4\)
Solution:\(\displaystyle f(0,0)=9\) is a local maximum.
20) \(\displaystyle f(x,y)=7x^2y+9xy^2\)
21) \(\displaystyle f(x,y)=3x^2−2xy+y^2−8y\)
Solution:Relative minimum located at \(\displaystyle (2,6)\).
22) \(\displaystyle f(x,y)=3x^2+2xy+y^2\)
23) \(\displaystyle f(x,y)=y2+xy+3y+2x+3\)
Solution:\(\displaystyle (1,−2)\) is a saddle point.
24) \(\displaystyle f(x,y)=x^2+xy+y^2−3x\)
25) \(\displaystyle f(x,y)=x^2+2y^2−x^2y\)
Solution:\(\displaystyle (2,1)\) and \(\displaystyle (−2,1)\) are saddle points; \(\displaystyle (0,0)\) is a relative minimum.
26) \(\displaystyle f(x,y)=x^2+y−e^y\)
27) \(\displaystyle f(x,y)=e^{−(x^2+y^2+2x)}\)
Solution:\(\displaystyle (−1,0)\) is a relative maximum.
28) \(\displaystyle f(x,y)=x^2+xy+y^2−x−y+1\)
29) \(\displaystyle f(x,y)=x^2+10xy+y^2\)
Solution:\(\displaystyle (0,0)\) is a saddle point.
30) \(\displaystyle f(x,y)=−x^2−5y^2+10x−30y−62\)
31) \(\displaystyle f(x,y)=120x+120y−xy−x^2−y^2\)
Solution:The relative maximum is at \(\displaystyle (40,40)\).
32) \(\displaystyle f(x,y)=2x^2+2xy+y^2+2x−3\)
33) \(\displaystyle f(x,y)=x^2+x−3xy+y^3−5\)
Solution:\(\displaystyle (\frac{1}{4},\frac{1}{2})\) is a saddle point and \(\displaystyle (1,1)\) is the relative minimum.
34) \(\displaystyle f(x,y)=2xye^{−x^2−y^2}\)
For the following exercises, determine the extreme values and the saddle points. Use a CAS to graph the function.
35) [T] \(\displaystyle f(x,y)=ye^x−e^y\)
Solution:A saddle point is located at \(\displaystyle (0,0).\)
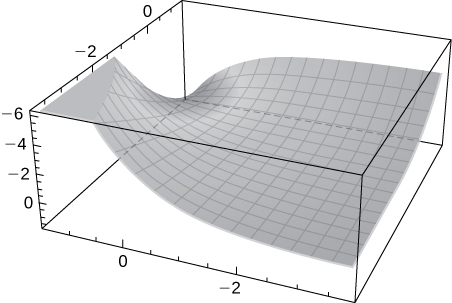
36) [T] \(\displaystyle f(x,y)=xsin(y)\)
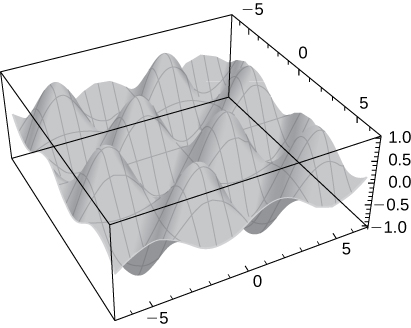
37) [T] \(\displaystyle f(x,y)=sin(x)sin(y),x∈(0,2π),y∈(0,2π)\)
Solution:There is a saddle point at \(\displaystyle (π,π),\) local maxima at \(\displaystyle (\frac{π}{2},\frac{π}{2})\) and \(\displaystyle (\frac{3π}{2},\frac{3π}{2})\), and local minima at \(\displaystyle (\frac{π}{2},\frac{3π}{2})\) and \(\displaystyle (\frac{3π}{2},\frac{π}{2})\).
Find the absolute extrema of the given function on the indicated closed and bounded set \(\displaystyle R\).
38) \(\displaystyle f(x,y)=xy−x−3y; R\) is the triangular region with vertices \(\displaystyle (0,0),(0,4),\) and \(\displaystyle (5,0)\).
39) Find the absolute maximum and minimum values of \(\displaystyle f(x,y)=x^2+y^2−2y+1\) on the region \(\displaystyle R={(x,y)∣x^2+y^2≤4}.\)
Solution:\(\displaystyle (0,1,0)\) is the absolute minimum and \(\displaystyle (0,−2,9)\) is the absolute maximum.
40) \(\displaystyle f(x,y)=x^3−3xy−y^3\) on \(\displaystyle R={(x,y):−2≤x≤2,−2≤y≤2}\)
41) \(\displaystyle f(x,y)=\frac{−2y}{x^2+y^2+1}\) on \(\displaystyle R={(x,y):x^2+y^2≤4}\)
Solution:There is an absolute minimum at \(\displaystyle (0,1,−1)\) and an absolute maximum at \(\displaystyle (0,−1,1)\).
42) Find three positive numbers the sum of which is \(\displaystyle 27\), such that the sum of their squares is as small as possible.
43) Find the points on the surface \(\displaystyle x^2−yz=5\) that are closest to the origin.
Solution:\(\displaystyle (\sqrt{5},0,0),(−\sqrt{5},0,0)\)
44) Find the maximum volume of a rectangular box with three faces in the coordinate planes and a vertex in the first octant on the line \(\displaystyle x+y+z=1\).
45) The sum of the length and the girth (perimeter of a cross-section) of a package carried by a delivery service cannot exceed \(\displaystyle 108\) in. Find the dimensions of the rectangular package of largest volume that can be sent.
Solution:\(\displaystyle 18\) by \(\displaystyle 36\) by \(\displaystyle 18\) in.
46) A cardboard box without a lid is to be made with a volume of \(\displaystyle 4\) ft3. Find the dimensions of the box that requires the least amount of cardboard.
47) Find the point on the surface \(\displaystyle f(x,y)=x^2+y^2+10\) nearest the plane \(\displaystyle x+2y−z=0.\) Identify the point on the plane.
Solution:\(\displaystyle (\frac{47}{24},\frac{47}{12},\frac{235}{24})\)
48) Find the point in the plane \(\displaystyle 2x−y+2z=16\) that is closest to the origin.
49) A company manufactures two types of athletic shoes: jogging shoes and cross-trainers. The total revenue from \(\displaystyle x\) units of jogging shoes and \(\displaystyle y\) units of cross-trainers is given by \(\displaystyle R(x,y)=−5x^2−8y^2−2xy+42x+102y,\) where \(\displaystyle x\) and \(\displaystyle y\) are in thousands of units. Find the values of \(\displaystyle x\) and \(\displaystyle y\) to maximize the total revenue.
Solution:\(\displaystyle x=3\) and \(\displaystyle y=6\)
50) A shipping company handles rectangular boxes provided the sum of the length, width, and height of the box does not exceed \(\displaystyle 96\)in. Find the dimensions of the box that meets this condition and has the largest volume.
51) Find the maximum volume of a cylindrical soda can such that the sum of its height and circumference is \(\displaystyle 120\) cm.
Solution:\(\displaystyle V=\frac{64,000}{π}≈20,372cm^3\)
14.8: Lagrange Multipliers
For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints.
f(x,y)=x2y;x2+2y2=6f(x,y)=x2y;x2+2y2=6
f(x,y,z)=xyz,x2+2y2+3z2=6f(x,y,z)=xyz,x2+2y2+3z2=6
maximum: 23√3,233, minimum: −23√3−233
f(x,y)=xy;4x2+8y2=16f(x,y)=xy;4x2+8y2=16
f(x,y)=4x3+y2;2x2+y2=1f(x,y)=4x3+y2;2x2+y2=1
maximum: (2√2,0,2–√),(22,0,2), minimum: (−2√2,0,−2–√)(−22,0,−2)
f(x,y,z)=x2+y2+z2,x4+y4+z4=1f(x,y,z)=x2+y2+z2,x4+y4+z4=1
f(x,y,z)=yz+xy,xy=1,y2+z2=1f(x,y,z)=yz+xy,xy=1,y2+z2=1
maximum: 32,32, minimum = 11
f(x,y)=x2+y2,(x−1)2+4y2=4f(x,y)=x2+y2,(x−1)2+4y2=4
f(x,y)=4xy,x29+y216=1f(x,y)=4xy,x29+y216=1
maxima: f(32√2,22–√)=24,f(322,22)=24, f(−32√2,−22–√)=24;f(−322,−22)=24; minima: f(−32√2,22–√)=−24,f(−322,22)=−24, f(32√2,−22–√)=−24f(322,−22)=−24
f(x,y,z)=x+y+z,1x+1y+1z=1f(x,y,z)=x+y+z,1x+1y+1z=1
f(x,y,z)=x+3y−z,x2+y2+z2=4f(x,y,z)=x+3y−z,x2+y2+z2=4
maximum: 211−−√211 at f(211√,611√,−211√);f(211,611,−211); minimum: −211−−√−211 at f(−211√,−611√,211√)f(−211,−611,211)
f(x,y,z)=x2+y2+z2,xyz=4f(x,y,z)=x2+y2+z2,xyz=4
Minimize f(x,y)=x2+y2f(x,y)=x2+y2 on the hyperbola xy=1.xy=1.
2.02.0
Minimize f(x,y)=xyf(x,y)=xy on the ellipse b2x2+a2y2=a2b2.b2x2+a2y2=a2b2.
Maximize f(x,y,z)=2x+3y+5zf(x,y,z)=2x+3y+5z on the sphere x2+y2+z2=19.x2+y2+z2=19.
192–√192
Maximize f(x,y)=x2−y2;x>0,y>0;g(x,y)=y−x2=0f(x,y)=x2−y2;x>0,y>0;g(x,y)=y−x2=0
The curve x3−y3=1x3−y3=1 is asymptotic to the line y=x.y=x. Find the point(s) on the curve x3−y3=1x3−y3=1 farthest from the line y=x.y=x.
(12√3,−12√3)(123,−123)
Maximize U(x,y)=8x4/5y1/5;4x+2y=12U(x,y)=8x4/5y1/5;4x+2y=12
Minimize f(x,y)=x2+y2,x+2y−5=0.f(x,y)=x2+y2,x+2y−5=0.
f(1,2)=5f(1,2)=5
Maximize f(x,y)=6−x2−y2−−−−−−−−−√,x+y−2=0.f(x,y)=6−x2−y2,x+y−2=0.
Minimize f(x,y,z)=x2+y2+z2,x+y+z=1.f(x,y,z)=x2+y2+z2,x+y+z=1.
f(13,13,13)=13f(13,13,13)=13
Minimize f(x,y)=x2−y2f(x,y)=x2−y2 subject to the constraint x−2y+6=0.x−2y+6=0.
Minimize f(x,y,z)=x2+y2+z2f(x,y,z)=x2+y2+z2 when x+y+z=9x+y+z=9 and x+2y+3z=20.x+2y+3z=20.
minimum: f(2,3,4)=29f(2,3,4)=29
For the next group of exercises, use the method of Lagrange multipliers to solve the following applied problems.
A pentagon is formed by placing an isosceles triangle on a rectangle, as shown in the diagram. If the perimeter of the pentagon is 1010 in., find the lengths of the sides of the pentagon that will maximize the area of the pentagon.

A rectangular box without a top (a topless box) is to be made from 1212 ft2 of cardboard. Find the maximum volume of such a box.
The maximum volume is 44 ft3. The dimensions are 1×2×21×2×2 ft.
Find the minimum and maximum distances between the ellipse x2+xy+2y2=1x2+xy+2y2=1 and the origin.
Find the point on the surface x2−2xy+y2−x+y=0x2−2xy+y2−x+y=0 closest to the point (1,2,−3).(1,2,−3).
(1,12,−3)(1,12,−3)
Show that, of all the triangles inscribed in a circle of radius RR (see diagram), the equilateral triangle has the largest perimeter.

Find the minimum distance from point (0,1)(0,1) to the parabola x2=4y.x2=4y.
1.01.0
Find the minimum distance from the parabola y=x2y=x2 to point (0,3).(0,3).
Find the minimum distance from the plane x+y+z=1x+y+z=1 to point (2,1,1).(2,1,1).
3–√3
A large container in the shape of a rectangular solid must have a volume of 480480 m3. The bottom of the container costs $5/m2 to construct whereas the top and sides cost $3/m2 to construct. Use Lagrange multipliers to find the dimensions of the container of this size that has the minimum cost.
Find the point on the line y=2x+3y=2x+3 that is closest to point (4,2).(4,2).
(25,195)(25,195)
Find the point on the plane 4x+3y+z=24x+3y+z=2 that is closest to the point (1,−1,1).(1,−1,1).
Find the maximum value of f(x,y)=sinxsiny,f(x,y)=sinxsiny, where xandyxandy denote the acute angles of a right triangle. Draw the contours of the function using a CAS.
1212

A rectangular solid is contained within a tetrahedron with vertices at
(1,0,0),(0,1,0),(0,0,1),(1,0,0),(0,1,0),(0,0,1), and the origin. The base of the box has dimensions x,y,x,y, and the height of the box is z.z. If the sum of x,y,andzx,y,andz is 1.0, find the dimensions that maximizes the volume of the rectangular solid.
[T] By investing x units of labor and y units of capital, a watch manufacturer can produce P(x,y)=50x0.4y0.6P(x,y)=50x0.4y0.6 watches. Find the maximum number of watches that can be produced on a budget of $20,000$20,000 if labor costs $100/unit and capital costs $200/unit. Use a CAS to sketch a contour plot of the function.
Roughly 3365 watches at the critical point (80,60)(80,60)



