11.3E: Exercises for The Dot Product
- Page ID
- 8631
For exercises 1-4, the vectors \(\vecs{u}\) and \(\vecs{v}\) are given. Calculate the dot product \(\vecs{u}\cdot\vecs{v}\).
1) \(\quad \vecs{u}=⟨3,0⟩, \quad \vecs{v}=⟨2,2⟩\)
- Answer:
- \(\vecs{u}\cdot\vecs{v}=6\)
2) \(\quad \vecs{u}=⟨3,−4⟩, \quad \vecs{v}=⟨4,3⟩\)
3) \(\quad \vecs{u}=⟨2,2,−1⟩, \quad \vecs{v}=⟨−1,2,2⟩\)
- Answer:
- \(\vecs{u}\cdot\vecs{v}=0\)
4) \(\quad \vecs{u}=⟨4,5,−6⟩, \quad \vecs{v}=⟨0,−2,−3⟩\)
For exercises 5-8, the vectors \(\vecs{a}, \,\vecs{b}\), and \(\vecs{c}\) are given. Determine the vectors \((\vecs{a}\cdot\vecs{b})\vecs{c}\) and \((\vecs{a}⋅\vecs{c})\vecs{b}.\) Express the vectors in component form.
5) \(\quad \vecs{a}=⟨2,0,−3⟩, \quad \vecs{b}=⟨−4,−7,1⟩, \quad \vecs{c}=⟨1,1,−1⟩\)
- Answer:
- \( (\vecs a⋅\vecs b)\vecs c=⟨−11,−11,11⟩; (\vecs a⋅\vecs c)b=⟨−20,−35,5⟩\)
6) \(\quad \vecs{a}=⟨0,1,2⟩, \quad \vecs{b}=⟨−1,0,1⟩, \quad \vecs{c}=⟨1,0,−1⟩\)
7) \(\quad \vecs{a}=\mathbf{\hat i} +\mathbf{\hat j} , \quad \vecs{b}=\mathbf{\hat i} −\mathbf{\hat k} , \quad \vecs{c}=\mathbf{\hat i} −2\mathbf{\hat k} \)
- Answer:
- \( (\vecs a⋅\vecs b)\vecs c=⟨1,0,−2⟩; (\vecs a⋅\vecs c)\vecs b=⟨1,0,−1⟩\)
8) \(\quad \vecs{a}=\mathbf{\hat i} −\mathbf{\hat j} +\mathbf{\hat k} , \quad \vecs{b}=\mathbf{\hat j} +3\mathbf{\hat k} , \quad \vecs{c}=−\mathbf{\hat i} +2\mathbf{\hat j} −4\mathbf{\hat k} \)
For exercises 9-12, two vectors are given.
a. Find the measure of the angle \(θ\) between these two vectors. Express the answer in radians rounded to two decimal places, if it is not possible to express it exactly.
b. Is \(θ\) an acute angle?
9) [T] \(\quad \vecs{a}=⟨3,−1⟩, \quad \vecs{b}=⟨−4,0⟩\)
- Answer:
- \( a. θ=2.82\) rad; \( b. θ\) is not acute.
10) [T] \(\quad \vecs{a}=⟨2,1⟩, \quad \vecs{b}=⟨−1,3⟩\)
11) \(\quad \vecs{u}=3\mathbf{\hat i}, \quad \vecs{v}=4\mathbf{\hat i} +4\mathbf{\hat j} \)
- Answer:
- \( a. θ=\frac{π}{4}\) rad; \( b. θ\) is acute.
12) \(\quad \vecs{u}=5\mathbf{\hat i}, \quad \vecs{v}=−6\mathbf{\hat i} +6\mathbf{\hat j} \)
For exercises 13-18, find the measure of the angle between the three-dimensional vectors \(\vecs{a}\) and \(\vecs{b}\). Express the answer in radians rounded to two decimal places, if it is not possible to express it exactly.
13) \(\quad \vecs{a}=⟨3,−1,2⟩, \quad \vecs{b}=⟨1,−1,−2⟩\)
- Answer:
- \( θ=\frac{π}{2}\)
14) \(\quad \vecs{a}=⟨0,−1,−3⟩, \quad \vecs{b}=⟨2,3,−1⟩\)
15) \(\quad \vecs{a}=\mathbf{\hat i} +\mathbf{\hat j} , \quad \vecs{b}=\mathbf{\hat j} −\mathbf{\hat k} \)
- Answer:
- \( θ=\frac{π}{3}\)
16) \(\quad \vecs{a}=\mathbf{\hat i} −2\mathbf{\hat j} +\mathbf{\hat k} , \quad \vecs{b}=\mathbf{\hat i} +\mathbf{\hat j} −2\mathbf{\hat k} \)
17) [T] \(\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} −2\mathbf{\hat k} , \quad \vecs{b}=\vecs v+\vecs w,\) where \(\quad \vecs{v}=−2\mathbf{\hat i} −3\mathbf{\hat j} +2\mathbf{\hat k} \) and \(\vecs{w}=\mathbf{\hat i} +2\mathbf{\hat k} \)
- Answer:
- \( θ\approx 2.00\) rad
18) [T] \(\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} +2\mathbf{\hat k} , \quad \vecs{b}=\vecs v−\vecs w,\) where \(\quad \vecs{v}=2\mathbf{\hat i} +\mathbf{\hat j} +4\mathbf{\hat k} \) and \(\vecs{w}=6\mathbf{\hat i} +\mathbf{\hat j} +2\mathbf{\hat k} \)
For exercises 19-22, determine whether the given vectors are orthogonal.
19) \(\quad \vecs{a}=⟨x,y⟩, \quad \vecs{b}=⟨−y, x⟩\), where \(x\) and \(y\) are nonzero real numbers
- Answer:
- Orthogonal
20) \(\quad \vecs{a}=⟨x, x⟩, \quad \vecs{b}=⟨−y, y⟩\), where \(x\) and \(y\) are nonzero real numbers
21) \(\quad \vecs{a}=3\mathbf{\hat i} −\mathbf{\hat j} −2\mathbf{\hat k} , \quad \vecs{b}=−2\mathbf{\hat i} −3\mathbf{\hat j} +\mathbf{\hat k} \)
- Answer:
- Not orthogonal
22) \(\quad \vecs{a}=\mathbf{\hat i} −\mathbf{\hat j} , \quad \vecs{b}=7\mathbf{\hat i} +2\mathbf{\hat j} −\mathbf{\hat k} \)
23) Find all two-dimensional vectors \(\vecs a\) orthogonal to vector \( \vecs b=⟨3,4⟩.\) Express the answer in component form.
- Answer:
- \( \vecs a=⟨−\frac{4α}{3},α⟩,\) where \( α≠0\) is a real number
24) Find all two-dimensional vectors \( \vecs a\) orthogonal to vector \( \vecs b=⟨5,−6⟩.\) Express the answer by using standard unit vectors.
25) Determine all three-dimensional vectors \( \vecs u\) orthogonal to vector \( \vecs v=⟨1,1,0⟩.\) Express the answer by using standard unit vectors.
- Answer:
- \( \vecs u=−α\mathbf{\hat i} +α\mathbf{\hat j} +β\mathbf{\hat k} ,\) where \( α\) and \( β\) are real numbers such that \( α^2+β^2≠0\)
26) Determine all three-dimensional vectors \(\vecs u\) orthogonal to vector \(\vecs v=\mathbf{\hat i} −\mathbf{\hat j} −\mathbf{\hat k} \). Express the answer in component form.
27) Determine the real number \(α\) such that vectors \(\vecs a=2\mathbf{\hat i} +3\mathbf{\hat j} \) and \(\vecs b=9\mathbf{\hat i} +α\mathbf{\hat j} \) are orthogonal.
- Answer:
- \(α=−6\)
28) Determine the real number \(α\) such that vectors \(\vecs a=−3\mathbf{\hat i} +2\mathbf{\hat j} \) and \(\vecs b=2\mathbf{\hat i} +α\mathbf{\hat j} \) are orthogonal.
29) [T] Consider the points \(P(4,5)\) and \(Q(5,−7)\), and note that \(O\) represents the origin.
a. Determine vectors \(\vecd{OP}\) and \(\vecd{OQ}\). Express the answer by using standard unit vectors.
b. Determine the measure of angle \(O\) in triangle \(OPQ\). Express the answer in degrees rounded to two decimal places.
- Answer:
- \(a. \vecd{OP}=4\mathbf{\hat i} +5\mathbf{\hat j} , \quad \vecd{OQ}=5\mathbf{\hat i} −7\mathbf{\hat j} ; \quad b. 105.8°\)
30) [T] Consider points \( A(1,1), B(2,−7),\) and \(C(6,3)\).
a. Determine vectors \( \vecd{BA}\) and \(\vecd{BC}\). Express the answer in component form.
b. Determine the measure of angle \(B\) in triangle \(ABC\). Express the answer in degrees rounded to two decimal places.
31) Determine the measure of angle \(A\) in triangle \(ABC\), where \(A(1,1,8), B(4,−3,−4),\) and \(C(−3,1,5).\) Express your answer in degrees rounded to two decimal places.
- Answer:
- \(68.33°\)
32) Consider points \(P(3,7,−2)\) and \(Q(1,1,−3).\) Determine the angle between vectors \(\vecd{OP}\) and \(\vecd{OQ}\). [Remember that \(O\) represents the origin.] Express the answer in degrees rounded to two decimal places.
For exercises 33-34, determine which (if any) pairs of the following vectors are orthogonal.
33) \(\quad\vecs u=⟨3,7,−2⟩, \quad \vecs v=⟨5,−3,−3⟩, \quad \vecs w=⟨0,1,−1⟩\)
- Answer:
- \(\vecs u\) and \(\vecs v\) are orthogonal; \(\vecs v\) and \(\vecs w\) are orthogonal, but \(\vecs u\) and \(\vecs w\) are not orthogonal.
34) \(\quad\vecs u=\mathbf{\hat i} −\mathbf{\hat k} , \quad \vecs v=5\mathbf{\hat j} −5\mathbf{\hat k} , \quad \vecs w=10\mathbf{\hat j} \)
35) Use vectors to show that a parallelogram with equal diagonals is a rectangle.
36) Use vectors to show that the diagonals of a rhombus are perpendicular.
37) Show that \(\vecs u⋅(\vecs v+\vecs w)=\vecs u⋅\vecs v+\vecs u⋅\vecs w\) is true for any vectors \(\vecs u, \vecs v\), and \(\vecs w\).
38) Verify the identity \(\vecs u⋅(\vecs v+\vecs w)=\vecs u⋅\vecs v+\vecs u⋅\vecs w\) for vectors \(\vecs u=⟨1,0,4⟩, \vecs v=⟨−2,3,5⟩,\) and \(\vecs w=⟨4,−2,6⟩\).
For exercises 39-41, determine \(\vecs u\cdot\vecs v\) using the given information.
39) \(\quad\|\vecs u\| = 5\), \(\quad\|\vecs v\| = 3\), and the angle between \(\vecs u\) and \(\vecs v\) is \(\pi/6\) rad.
- Answer:
- \(\vecs u \cdot \vecs v = (5)(3)\cos \frac{\pi}{6} = 15\cdot\frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{2} \)
40) \(\quad\|\vecs u\| = 20\), \(\quad\|\vecs v\| = 15\), and the angle between \(\vecs u\) and \(\vecs v\) is \(5\pi/4\) rad.
41) \(\quad\|\vecs u\| = 7\), \(\quad\|\vecs v\| = 12\), and the angle between \(\vecs u\) and \(\vecs v\) is \(\pi/2\) rad.
- Answer:
- \(\vecs u \cdot \vecs v = (7)(12)\cos \frac{\pi}{2} = 84\cdot0 = 0 \)
42) Considering the definition of the dot product, \(\vecs u\cdot\vecs v = \|\vecs u\|\|\vecs v\|\cos \theta\), where \(\theta\) is the angle between \(\vecs u\) and \(\vecs v\), what can you say about the angle \(\theta\) between two nonzero vectors \(\vecs u\) and \(\vecs v\) if:
a. \(\quad\vecs u \cdot \vecs v > 0\)?
b. \(\quad\vecs u \cdot \vecs v < 0\)?
c. \(\quad\vecs u \cdot \vecs v = 0\)?
In exercises 43-45, you are given the vertices of a triangle. Use dot products to determine whether each triangle is acute, obtuse, or right.
43) \(\quad (2, 3, 0), \, (3, 1, -2), \, (-1, 4, 5)\)
- Answer:
- Label the points \(P\), \(Q\) and \(R\). Then determine the vectors \(\vecd{PQ}\) and \(\vecd{PR}\).
Here we see that, if \(P = (2, 3, 0), \, Q = (3, 1, -2)\) and \(R = (-1, 4, 5)\), so we have \(\vecd{PQ} = <1,-2,-2>\) and \(\vecd{PR} = <-3,1,5>\).
Then \(\vecd{PQ} \cdot \vecd{PR} = -15 < 0\), so angle \(QPR\) is obtuse. Therefore this triangle must be an obtuse triangle.
44) \(\quad (5, 1, 0), \, (7, 1, 1), \, (6, 3, 2)\)
45) \(\quad (6, 1, 4), \, (3, 2, -1), \, (2, 3, 1)\)
- Solution:
- Label the points \(P\), \(Q\) and \(R\). Then determine the vectors \(\vecd{PQ}\) and \(\vecd{PR}\).
Here we see that, if \(P = (6, 1, 4), \, Q = (3, 2, -1)\) and \(R = (2, 3, 1)\), so we have \(\vecd{PQ} = <-3,1,-5>\) and \(\vecd{PR} = <-4,2,-3>\).
Then \(\vecd{PQ} \cdot \vecd{PR} = 29 > 0\), so angle \(QPR\) is acute. This triangle could still be any of the three types, so we need to check another angle.
Considering angle \(PQR\) we find \(\vecd{QP} = <3,-1,5>\) and \(\vecd{QR} = <-1,1,2>\), so \(\vecd{QP} \cdot \vecd{QR} = 6 > 0\), showing angle \(PQR\) is also acute.
We then must check the third angle to determine whether this is a right triangle or an acute triangle.
To check angle \(PRQ\) we find \(\vecd{RP} = <4,-2,3>\) and \(\vecd{RQ} = <1,-1,-2>\), giving us \(\vecd{RP} \cdot \vecd{RQ} = 0\). Angle \(PRQ\) is thus a right angle.
Therefore this triangle is a right triangle.
46) Which of the following operations are allowed for nonzero vectors \(\vecs u\), \(\vecs v\), and \(\vecs w\), and which are not. Explain your reasoning.
a. \(\vecs u + \left(\vecs v \cdot \vecs w\right)\) b. \(\left(\vecs u \cdot \vecs v\right) \cdot \vecs w\) c. \(\left(\vecs u \cdot \vecs v\right) \vecs w\)
d. \(\left(\vecs u + \vecs v\right) \cdot \vecs w\) e. \(\left(\vecs u + \vecs v\right) \cdot \|\vecs w\|\) f. \(\|\vecs u + \vecs v\| \|\vecs w\|\)
Projections
For the exercises 47-50, given the vectors \(\vecs u\) and \(\vecs v\):
a. Find the vector projection \(\text{Proj}_\vecs{u}\vecs v\) of vector \(\vecs v\) onto vector \(\vecs u\) and the component of \(\vecs v\) that is orthogonal to \(\vecs u\), i.e., \(\vecs v_\text{perp}\). Express your answers in component form.
b. Find the scalar projection \(\text{comp}_\vecs{u}\vecs v = \| \text{Proj}_\vecs{u}\vecs v \|\) of vector \(\vecs v\) onto vector \(\vecs u\).
c. Find the vector projection \(\text{Proj}_\vecs{v}\vecs u\) of vector \(\vecs u\) onto vector \(\vecs v\) and the component of \(\vecs u\) that is orthogonal to \(\vecs v\), i.e., \(\vecs u_\text{perp}\). Express your answers in unit vector form.
d. Find the scalar projection \(\text{comp}_\vecs{v}\vecs u\) of vector \(\vecs u\) onto vector \(\vecs v\).
47) \(\quad\vecs u=5\mathbf{\hat i} +2\mathbf{\hat j} , \quad \vecs v=2\mathbf{\hat i} +3\mathbf{\hat j} \)
- Answer:
- a. \(\text{Proj}_\vecs{u}\vecs v =⟨\frac{80}{29},\frac{32}{29}⟩\) and \(\vecs v_\text{perp} = <-\frac{22}{29}, \frac{55}{29}>\); b. \(\text{comp}_\vecs{u}\vecs v=\frac{16}{\sqrt{29}} = \frac{16\sqrt{29}}{29};\)
c. \(\text{Proj}_\vecs{v}\vecs u = \frac{32}{13}\mathbf{\hat i} + \frac{48}{13}\mathbf{\hat j} \) and \(\vecs u_\text{perp} = \frac{33}{13}\mathbf{\hat i} - \frac{22}{13}\mathbf{\hat j} \); d. \(\text{comp}_\vecs{v}\vecs u=\frac{16}{\sqrt{13}}=\frac{16\sqrt{13}}{13}\)
48) \(\quad\vecs u=⟨−4,7⟩,\quad \vecs v=⟨3,5⟩\)
49) \(\quad\vecs u=3\mathbf{\hat i} +2\mathbf{\hat k} , \quad \vecs v=2\mathbf{\hat j} +4\mathbf{\hat k} \)
- Answer:
- a. \(\text{Proj}_\vecs{u}\vecs v =⟨\frac{24}{13},0,\frac{16}{13}⟩\) and \(\vecs v_\text{perp} = <-\frac{24}{13}, 2, \frac{36}{13}> \); b. \(\text{comp}_\vecs{u}\vecs v=\frac{8}{\sqrt{13}}=\frac{8\sqrt{13}}{13}\)
c. \(\text{Proj}_\vecs{v}\vecs u =\frac{4}{5}\mathbf{\hat j} + \frac{8}{5}\mathbf{\hat k} \) and \(\vecs u_\text{perp} = 3\mathbf{\hat i} - \frac{4}{5}\mathbf{\hat j} + \frac{2}{5}\mathbf{\hat k} \); d. \(\text{comp}_\vecs{v}\vecs u=\frac{\sqrt{80}}{5} = \frac{4\sqrt{5}}{5};\)
50) \(\quad\vecs u=⟨4,4,0⟩, \quad \vecs v=⟨0,4,1⟩\)
51) Consider the vectors \(\vecs u=4\mathbf{\hat i} −3\mathbf{\hat j} \) and \(\vecs v=3\mathbf{\hat i} +2\mathbf{\hat j} .\)
a. Find the component form of vector \(\text{Proj}_\vecs{u}\vecs v\) that represents the projection of \(\vecs v\) onto \(\vecs u\).
b. Write the decomposition \(\vecs v=\vecs w+\vecs q\) of vector \(\vecs v\) into the orthogonal components \(\vecs w\) and \(\vecs q\), where \(\vecs w\) is the projection of \(\vecs v\) onto \(\vecs u\) and \(\vecs q\) is the vector component of \(\vecs v\) orthogonal to the direction of \(\vecs u\). That is, \( \vecs q = \vecs v_\text{perp}\).
- Answer:
- a. \(\text{Proj}_\vecs{u}\vecs v=⟨\frac{24}{25},−\frac{18}{25}⟩\); b. \(\vecs q = \vecs v_\text{perp} =⟨\frac{51}{25},\frac{68}{25}⟩\),
\(\vecs v =\vecs w+\vecs q= \text{Proj}_\vecs{u}\vecs v + \vecs v_\text{perp} =⟨\frac{24}{25},−\frac{18}{25}⟩+⟨\frac{51}{25},\frac{68}{25}⟩\)
So we have that, \(\vecs v = ⟨\frac{24}{25},−\frac{18}{25}⟩+⟨\frac{51}{25},\frac{68}{25}⟩\).
52) Consider vectors \(\vecs u=2\mathbf{\hat i} +4\mathbf{\hat j} \) and \(\vecs v=4\mathbf{\hat j} +2\mathbf{\hat k} .\)
a. Find the component form of vector \(\vecs w=\text{Proj}_\vecs{u}\vecs v\) that represents the projection of \(\vecs v\) onto \(\vecs u\).
b. Write the decomposition \(\vecs v=\vecs w+\vecs q\) of vector \(\vecs v\) into the orthogonal components \(\vecs w\) and \(\vecs q\), where \(\vecs w\) is the projection of \(\vecs v\) onto \(\vecs u\) and \(\vecs q\) is a vector orthogonal to the direction of \(\vecs u\).
53) A \(50,000\)-pound truck is parked on a hill with a \(5°\) slope above the horizontal (in the positive \(x\)-direction). Considering only the force due to gravity, find
a. the component of the weight of the truck that is pulling the truck down the hill (aligned with the road)
b. the component of the weight of the truck that is perpendicular to the road.
c. the magnitude of the force needed to keep the truck from rolling down the hill
d. the magnitude of the force that is perpendicular to the road.
- Solution:
- Let \(\vecs F\) be the force due to gravity on the truck (its weight) and let \(\vecs r\) be the unit vector pointing up the hill to the right.
Then
a. the component of the weight of the truck that is pulling the truck down the hill is \(\text{Proj}_\vecs{r}\vecs F\).
Now \(\vecs F = -50,000\mathbf{\hat j} \quad\text{and}\quad \vecs r = \cos 5°\,\mathbf{\hat i} + \sin 5°\,\mathbf{\hat j} \) and \(\vecs F\cdot\vecs r = -50,000\sin 5° \approx -4357.78714\)
Note that \(\|\vecs r\| = 1\).
Then: \(\quad\,\text{Proj}_\vecs{r}\vecs F = \left(\frac{\vecs F\cdot\vecs r}{\|\vecs r\|^2}\right)\vecs r \quad = \left(-50,000\sin 5°\right)\vecs r \quad=\quad -50000\sin 5° \cos 5° \,\mathbf{\hat i} - 50000\sin^2 5° \,\mathbf{\hat j} \).
Using the identity, \(\sin 2\theta = 2\cos \theta \sin \theta\), we can simplify this as
\(\text{Proj}_\vecs{r}\vecs F = -25000\sin 10° \,\mathbf{\hat i} - 50000\sin^2 5°\, \mathbf{\hat j} \quad\approx\quad -4341.2\,\mathbf{\hat i} - 379.8\,\mathbf{\hat j} \).
b. the component of the weight of the truck that is perpendicular to the road is \(\vecs F_\text{perp}\).
Since we know that \(\vecs F = \text{Proj}_\vecs{r}\vecs F+\vecs F_\text{perp}\), we have that \(\vecs F_\text{perp} = \vecs F - \text{Proj}_\vecs{r}\vecs F\).
So \(\quad \vecs F_\text{perp} = -50000\mathbf{\hat j} - \left( -25000\sin 10° \,\mathbf{\hat i} - 50000\sin^2 5°\, \mathbf{\hat j} \right)\)
\(= 25000\sin 10° \,\mathbf{\hat i} + \left(50000\sin^2 5° - 50000\right)\mathbf{\hat j} = 25000\sin 10° \,\mathbf{\hat i} - 50000\cos^2 5° \,\mathbf{\hat j} \quad\approx\quad 4341.2\,\mathbf{\hat i} - 49620.2\,\mathbf{\hat j} \).
c. the magnitude of the force needed to keep the truck from rolling down the hill is \(\| \text{Proj}_\vecs{r}\vecs F \| = 50,000\sin 5°\) lbs \(\approx 4357.8\) lbs. Note that this force is actually the negative of the projection vector, but its magnitude is the same.
d. the magnitude of the truck's weight that is perpendicular to the road is \( \| \vecs F_\text{perp} \| \approx 49809.7\) lbs.
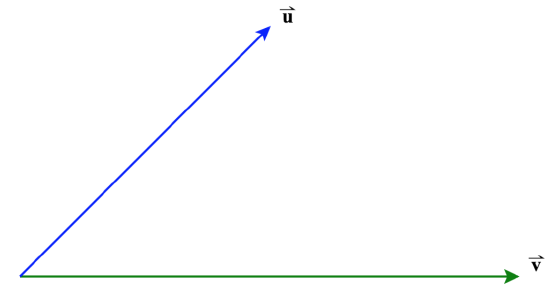
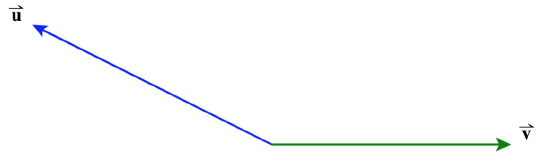
54) Given the vectors \(\vecs u\) and \(\vecs v\) shown in each diagram below, draw in \(\text{Proj}_\vecs{v}\vecs u\) and \( \vecs u_\text{perp} \).
Work
55) Find the work done by force \(\vecs F=⟨5,6,−2⟩\) (measured in Newtons) that moves a particle from point \(P(3,−1,0)\) to point \(Q(2,3,1)\) along a straight line (the distance is measured in meters).
- Answer:
- \(17\,\text{N⋅m}\)
56) [T] A sled is pulled by exerting a force of 100 N on a rope that makes an angle of \(25°\) with the horizontal. Find the work done in pulling the sled 40 m. (Round the answer to one decimal place.)
57) [T] A father is pulling his son on a sled at an angle of \(20°\) with the horizontal with a force of 25 lb (see the following image). He pulls the sled in a straight path of 50 ft. How much work was done by the man pulling the sled? (Round the answer to the nearest integer.)
- Answer:
- 1175 ft⋅lb
58) [T] A car is towed using a force of 1600 N. The rope used to pull the car makes an angle of 25° with the horizontal. Find the work done in towing the car 2 km. Express the answer in joules (\(1\) J\(=1\) N⋅m) rounded to the nearest integer.
59) [T] A boat sails north aided by a wind blowing in a direction of \( N30°E\) with a magnitude of 500 lb. How much work is performed by the wind as the boat moves 100 ft? (Round the answer to two decimal places.)
- Answer:
- \(25000\sqrt{3}\) ft-lbs \(\approx 43,301.27\) ft-lbs
- Solution:
- Vector representing the wind: \(\vecs w = 500\cos 60^{\circ} \mathbf{\hat i} + 500\sin 60^{\circ} \mathbf{\hat j}\)
Vector representing the displacement to the north: \(\vecs d = 100 \mathbf{\hat j}\)
Work done by the wind: \(W = \vecs w \cdot \vecs d = 25000\sqrt{3}\) ft-lbs \(\approx 43,301.27\) ft-lbs
Other Applications of the Dot Product
60) [T] Find the vectors that join the center of a clock to the hours 1:00, 2:00, and 3:00. Assume the clock is circular with a radius of 1 unit.
61) A methane molecule has a carbon atom situated at the origin and four hydrogen atoms located at points \(P(1,1,−1),Q(1,−1,1),R(−1,1,1),\) and \(S(−1,−1,−1)\) (see figure).
a. Find the distance between the hydrogen atoms located at \(P\)and \(R\).
b. Find the angle between vectors \(\vecd{OS}\) and \(\vecd{OR}\) that connect the carbon atom with the hydrogen atoms located at \(S\) and \(R\), which is also called the bond angle. Express the answer in degrees rounded to two decimal places.
- Answer:
- \(a. 2\sqrt{2}; \quad b. 109.47°\)
62) Vector \(\vecs p=⟨150,225,375⟩\) represents the price of certain models of bicycles sold by a bicycle shop. Vector \(\vecs n=⟨10,7,9⟩\) represents the number of bicycles sold of each model, respectively. Compute the dot product \(\vecs p⋅\vecs n\) and state its meaning.
63) [T] Two forces \(\vecs F_1\) and \(\vecs F_2\) are represented by vectors with initial points that are at the origin. The first force has a magnitude of 20 lb and passes through the point \(P(1,1,0)\). The second force has a magnitude of 40 lb and passes through the point \(Q(0,1,1)\). Let \(\vecs F\) be the resultant force of forces \(\vecs F_1\) and \(\vecs F_2\).
a. Find the magnitude of \(\vecs F\). (Round the answer to one decimal place.)
b. Find the direction angles of \(\vecs F\). (Express the answer in degrees rounded to one decimal place.)
- Answer:
- \( a. ∥\vecs F_1+\vecs F_2∥=52.9\) lb; b. The direction angles are \(α=74.5°,\,β=36.7°,\) and \( γ=57.7°.\)
64) [T] Consider \(\vecs r(t)=⟨\cos t,\sin t,2t⟩\) the position vector of a particle at time \(t∈[0,30]\), where the components of \(\vecs r\) are expressed in centimeters and time in seconds. Let \(\vecd{OP}\) be the position vector of the particle after 1 sec.
a. Show that all vectors \(\vecd{PQ}\), where \(Q(x,y,z)\) is an arbitrary point, orthogonal to the instantaneous velocity vector \(\vecs v(1)\) of the particle after 1 sec, can be expressed as \( \vecd{PQ}=⟨x−\cos 1,y−\sin 1,z−2⟩\), where \(x\sin 1−y\cos 1−2z+4=0.\) The set of point \(Q\) describes a plane called the normal plane to the path of the particle at point \(P\).
b. Use a CAS to visualize the instantaneous velocity vector and the normal plane at point \(P\) along with the path of the particle.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Exercises and LaTeX edited by Paul Seeburger. Problems 39-46 and 53 & 54 were created by Paul Seeburger.
Solution to Problem 59 also was added by Paul Seeburger.

