4.E: Basic Concepts of Euclidean Geometry (Exercises)
- Page ID
- 4898
Exercise \(\PageIndex{1}\): Similarity
Assess whether each of the following statement is true or false and justify your answer.
- Any two equilateral triangles are similar.
- Any two isosceles triangles are similar.
- Any two squares are similar.
- Any two rectangles are similar.
- Any two pentagons are similar.
- Any two polygons are similar.
Exercise \(\PageIndex{2}\): Area
Starting with the formula for the area of a triangle, show how to obtain the formula for the area of a parallelogram and the area of a hexagon.
Exercise \(\PageIndex{3}\): Interior angle
Find the general formula for the center angle in a regular n-sided polygon? Justify your answer.
Find the general formula for the exterior angle in a regular n-sided polygon? Justify your answer.
Exercise \(\PageIndex{4}\): Triangles
Prove or disprove the following: an equilateral triangle is an isosceles triangle.
explain why an equilateral triangle is not a scalene triangle?
Exercise \(\PageIndex{5}\): True or False
Explain why the following statements below are true.
- A square is a rectangle.
- A rectangle is a parallelogram.
- A square is a kite.
- A parallelogram is a trapezoid.
Exercise \(\PageIndex{6}\): Angles
Given cutout sheets with angles \(40^{\circ}, 55^{\circ }\) and \(85^{\circ}\). By adding or subtracting angles, construct other angles that measure \(15^{\circ}, 30^{\circ}, 70^{\circ}, 95^{\circ} \)and \(100^{\circ}.\)
Can you construct an angle that measures \( 75^{\circ}? \)Explain how or say why not.
Exercise \(\PageIndex{7}\): Converse of the Pythagorean Theorem
State the statement for the converse of the Pythagorean Theorem. Is this statement true or false? Justify your answer.
Exercise \(\PageIndex{8}\): Venn diagram
Create a Venn diagram to illustrate the types of quadrilaterals, listed in this section.
Exercise \(\PageIndex{9}\): Parallelogram
Let \((a; b); ((0; c); (d:e); (f; 0)\) be vertices of a quadrilateral. Show that if you take the midpoints of any quadrilateral and connect them in turn, you will always get a parallelogram.
Exercise \(\PageIndex{10}\): Venn Triangles
Express the relationship between scalene, isosceles and equilateral triangles with Venn diagram.
Exercise \(\PageIndex{11}\): Angles
Consider the figure:
Given that \( a= 47^{\circ}, \) and \(c= 55^{circ}.\)
Find other listed angles.
Exercise \(\PageIndex{12}\):
Refer to the cube picture above.
Name the following:
1.Two parallel line segments.
Exercise \(\PageIndex{13}\): Inner Circle
Find the area between the perimeter of this square and the unit circle.
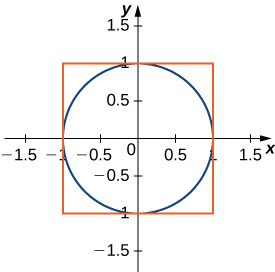
- Answer
-
\(1- \pi\)
Exercise \(\PageIndex{14}\): Outer Circle
Find the area between the perimeter of the unit circle and the triangle created from connecting the points \((0,1), (−\frac{4}{5}, −\frac{3}{5}) \)and \(\displaystyle (\frac{4}{5}, −\frac{3}{5}) \), as seen in the following figure.
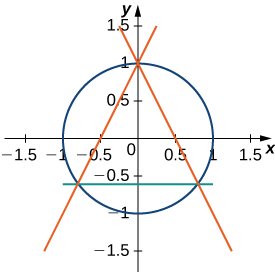
- Answer
-
(\displaystyle π−\frac{32}{25}\)
Exercise \(\PageIndex{15}\): Reuleaux triangle
The Reuleaux triangle consists of an equilateral triangle and three regions, each of them bounded by a side of the triangle and an arc of a circle of radius \(s \) centered at the opposite vertex of the triangle. Show that the area of the Reuleaux triangle in the following figure of side length \(s\) is \(\frac{s^2}{2}(\pi - \sqrt{3})\).

Exercise \(\PageIndex{16}\):lunes of Alhazen
Show that the area of the lunes of Alhazen, the two blue lunes in the following figure, is the same as the area of the right triangle ABC. The outer boundaries of the lunes are semicircles of diameters \(AB\) and \(AC\) respectively, and the inner boundaries are formed by the circumcircle of the triangle \(ABC\).

By Illuyanka (Own work) [GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons
Exercises 13-16 are from
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


