0.1: Real numbers

Real number arithmetic

Rules

1. The distributive law: If \(a,b\) and \(c\) are real numbers, then \[a(b+c)=ab+ac\] and \[(b+c)a=ba+ca.\]
2. The commutative laws: If \(a\) and \(b\) are real numbers, then \[ab=ba\] and \[a+b=b+a.\]
3. The associative law: If \(a,b\) and \(c\) are real numbers, then \[a+(b+c)=(a+b)+c\] and \[a(bc)=(ab)c.\]
4. The existence of \(0\): The real number \(0\) exists so that, for any real number \(a\), \[a+0=0+a=a.\]
5. The existence of \(1\): The real number \(1\) exists so that, for any real number \(a\), \[a \cdot 1=1 \cdot a=a.\]
6. Subtraction: For each real number \(a,\) there exists a real number \(-a,\) so that \[a+(-a)=0=(-a)+a.\]
7. Division: For each nonzero real number \(a,\) there exists a real number \(\displaystyle\frac{1}{a},\) so that \[a\left(\frac{1}{a}\right)=\left(\frac{1}{a}\right)a=1.\]

The laws above form the foundation of arithmetic and algebra of real numbers. They are the laws that we have accepted and used with no reserve. They are mentioned
here to encourage the reader to develop an appreciation for them and an awareness that they must be respected in all calculations involving real numbers.

The partitioning of the real number system

The collection of all real numbers contains a number of important sets. These are introduced next together with the appropriate standard notation.

1. The collection of counting numbers otherwise known as the collection of natural numbers is usually denoted by \(\mathbb{N}.\) We write \[\bf{\mathbb{N}} = \{ 1,2,3,4, \dots\}.\]
2. The collection of the integers is usually denoted by \(\mathbb{Z}\) and we write \[\bf{\mathbb{Z}} = \{ \dots,-3,-2,-1,0,1,2,3,4, \dots\}.\] Notice that \(\bf{\mathbb{N}}\) is properly contained in \(\mathbb{Z},\) denoted by \[{\mathbb{N}} \subsetneqq \mathbb{Z}.\]
3. The collection of all rational numbers (fractions) is usually denoted by \(\mathbb{Q}\) and We write \[\bf{\mathbb{Q}} = \left\{ \frac{a}{b}: a \mbox{ and }b \mbox{ are integers}, \, b \ne 0 \right\}.\] Notice that \(\bf{\mathbb{Z}}\) is properly contained in \(\bf{\mathbb{Q}}\) That is, \[{\mathbb{Z}} \subsetneqq \mathbb{Q}.\]
4. The collection of all irrational numbers is denoted by \(\bf{\mathbb{I}}\). This set contains all the real numbers which are not rational numbers. The rational numbers and irrational numbers have no elements in common. That means \[\bf{\mathbb{Q}} \cap \mathbb{I} = \emptyset.\]
5. The collection of all real numbers is denoted by \(\mathbb{R}\). This set contains all of the rational numbers and all of the irrational numbers. We write \[\bf{\mathbb{Q}} \cup \mathbb{I} = \mathbb{R}.\]

Definitions

1. A real number is called positive if it is greater than \(0\).
2. A real number is called non-negative if it is greater than or equal to \(0\).
3. An integer \(n\) is an even number if there is an integer \(m\) such that \(n=2m\).
4. An integer \(n\) is an odd number if there is an integer \(m\) such that \(n=2m+1\).

Special properties of the real numbers

It is worthwhile mentioning the following three properties:

Property \(\PageIndex{1}\)

The collection of real numbers has an order:

Given any two distinct real numbers \(a\) and \(b\), one of the following statements
will be true:

1. \(a<b,\)
2. \(b<a.\)

Example \(\PageIndex{1}\):

Consider the real numbers \(3.111\) and \(3.11101,\) it is not difficult to see that
\[3.111<3.11101.\]

Property \(\PageIndex{1}\)

The collection of the real numbers is complete:

Given any two distinct real numbers, there will always be a third real number that will lie in between
the two given.

Example \(\PageIndex{2}\):

Given the real numbers \(1.99999\) and \(1.999991,\) we can find the real number \(1.9999905\) which certainly lies in between the two.

Property\(\PageIndex{1}\)

The collection of the real numbers has neither the greatest element nor does it have the least element.

Useful hints for calculations without your calculator

Often in calculations, multiplication and division will be necessary, and although calculators are now available to help us through these chores, it is useful to develop a facility with these two operations. To this end, we conclude here some very useful facts.

1. An integer is an even number if and only if it is divisible by \(2.\)

2. An integer is divisible by \(3\) if and only if the sum of its digits is divisible by \(3.\)

Example \(\PageIndex{3}\):

\(3579\) is divisible by \(3\) since the sum of its digits is \(24\) which is divisible by \(3.\)

\(476911\) is not divisible by \(3\) since the sum of its digits is \(28\) which is not divisible by \(3.\)

3. An integer is divisible by \(5\) if and only if its last digit (the units digit) is either \(0\) or \(5.\)

Example \(\PageIndex{4}\):

\(27795\) and \(46790\) are both divisible by \(5.\)

\(3714\) is not divisible by \(5\) since its last digit (the units digit) is \(4.\)

4. Given any integer, if the difference between the sum of every other digit and the sum of the digits which remain is divisible by \(11\), then the integer is itself divisible by \(11\).

Example \(\PageIndex{5}\):

\(46791272\) is divisible by \(11\), since
\((4+7+1+7)=19\) and \((6+9+2+2)=19,\) \((4+7+1+7)-(6+9+2+2)=0\) and \(46791272\) is divisible by \(11.\)

\(9123917\) is divisible by \(11\), since
\(9+2+9+7=27\) and \(1+3+1=5,\) \((9+2+9+7)-(1+3+1)=22,\) which is divisible by \(11.\)

Intervals on the real line

\( \bf{\mathbb{R}}=(-\infty,\infty)\) in keeping with the fact that the collection of all real numbers has neither a least element nor a greatest element.

The symbol \(\infty\) does not represent a real number, but is used to denote the open endedness of the set.

1. For real numbers \(a\) and \(b\), with \(a<b,\) \(\{x \in \mathbb{R}: a<x<b \}\) which is denoted by \((a,b).\)

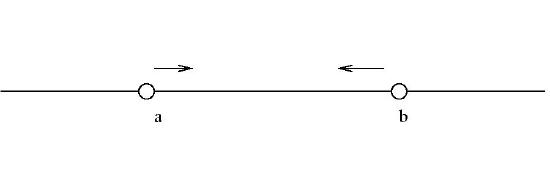
This is an open interval since the end-points of the interval are not contained in the interval.

2. For real numbers \(a\) and \(b\), with \(a<b,\) \(\{x \in \mathbb{R}: a\leq x \leq b \}\}\) which is denoted by \([a,b].\)

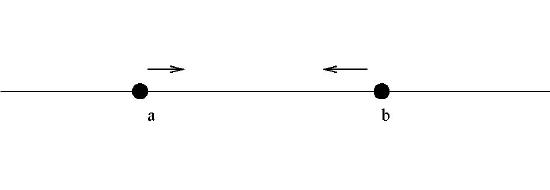
This is a closed interval since the end-points of the interval are contained in the interval.

3. For real numbers \(a\) and \(b\), with \(a<b,\) \(\{x \in \mathbb{R}: a<x \leq b \}\}\) which is denoted by \((a,b].\)

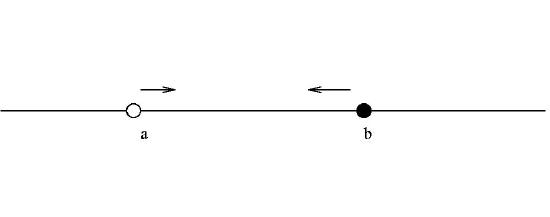
and \(\{x \in \mathbb{R}: a \leq x <b \}\}\) which is denoted by \([a,b).\)

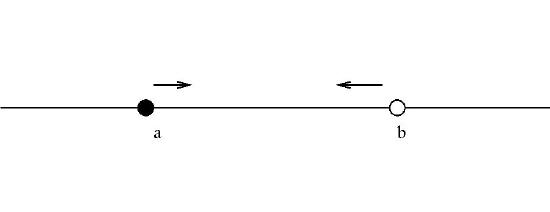
These are half open or half closed intervals since only one of the end-points must be included in the interval.

4. For real numbers \(a\) and \(b\), with \(a<b,\) \(\{x \in \mathbb{R}: x>b \}\}\) which is denoted by \((b,\infty).\)

\(\{x \in \mathbb{R}: x<b \}\}\) which is denoted by \((-\infty,b).\)

This notation must not be confused with the notation adopted for representing a point in the plane. Both are used freely in the literature and usually the reader should find it easy to distinguish between the two.

The partial order \(<\) on the set of all real numbers

Partial ORDER

If \(a,b\) and \(c\) are real numbers, then the following statements are true:

1. If \(a<b\) and \(b<c\) then \(a<c.\)
2. If \(a<b\), then for any real number \(c\), \(a+c<b+c\).
3. If \(a<b\) and \(c>0\) then \(ac<bc.\)
4. If \(a<b\) and \(c<0\) then \(ac>bc.\)

Example \(\PageIndex{6}\):

\(2<3\) and \(4<6.\)

Example \(\PageIndex{7}\):

\(2<3\) and \(-4>-6.\)

The absolute value

Definition

For any real number \(x\) the absolute value of \(x\) is denoted by \(|x|\) and defined by
\[|x|= \left\{\begin{array}{cc}
x& \mbox{ if } x\geq 0,\\
-x& \mbox{ if } x< 0.
\end{array}
\right.\]

Consequently we see that \(|-2|=|2|=2.\)

Rules

For real numbers \(a,b\) and \(c,\) the following hold:

1. \(|a| \geq 0,\) with equality when \(a=0.\)
2. \(|a^2|=a^2=|a|^2.\)
3. \(|ab|=|a| \cdot |b|.\)
4. This is a special case of above . If \(k\) is positive real number, then \(|ka|=k \cdot |a|.\)
5. \(\left|\displaystyle\frac{a}{b}\right|=\displaystyle\frac{|a|}{|b|},\) provided \(b \ne 0.\)
6. \( |a+b| \leq |a|+|b|.\)

A few examples to emphasize the importance of applying these rules as stated are given below.

Example \(\PageIndex{8}\):

\begin{eqnarray}
|6-2|&=&|6+(-2)| \nonumber \\
&=&|4|=4 .\nonumber\\
\mbox{Yet } |6|+|-2|&=&6+2=8.\nonumber\\
\mbox{Clearly then } |6-2| &<&|6|+|-2|.\nonumber
\end{eqnarray}

In rule 4, it is necessary that our choice of \(k\) be positive number. For example if \(k=-2,\)
\[|(-2)3|=|-2|\cdot |3|=6.\]
More generally, for any real number \(b,\)
\[|(-2)b|=|-2|\cdot |b|=2|b|.\]

Laws of exponents

Rules

For real numbers \(a,b,m\) and \(n,\) with \(a\ne 0\) and \(b\ne 0,\) the following rules hold:

1. \(a^m a^n=a^{m+n}\)

2. \(\displaystyle \frac{a^m}{a^n}=a^{m-n}\)

3. \(a^0=1\)

4. \((ab)^n=a^nb^n\)

5. \(\left(\displaystyle \frac{a}{b}\right)^n=\displaystyle \frac{a^n}{b^n}\)

6. \(\left( a^m \right)^n=a^{mn}\)

7. \(\displaystyle \frac{1}{a^n}=a^{-n}\)

Square roots

For any positive real number \(a,\) we can find another real number \(b,\) with the property that \[(b)(b)=a.\]

In this case \(b\) is called the square root of \(a,\) and \(b= \sqrt{a}\) means that \(b\) is the positive square root of \(a.\)

Rules

For positive real numbers \(a\) and \(b\),

1. \( \sqrt{a}\sqrt{a}=a\)

2. \( \sqrt{a}\sqrt{b}=\sqrt{ab}\)

3. \( \displaystyle \frac{\sqrt{a}}{\sqrt{b}}=\displaystyle\sqrt\frac{a}{b}\)

4. \( \sqrt{a^2}=|a|\)

If \(k\) is a positive real number, then \(\sqrt{k^2a}=k \sqrt{a}\)

5. \(\sqrt{a}=a^{1/2}\)

6. \(\sqrt[n]{a}=a^{1/n}\)

Caution

Except in special cases, \(\sqrt{(a^2+b^2)}\ne a+b,\mbox{ for positive real numbers.}\)

In particular, \(\sqrt{(3^2+4^2)}=\sqrt{25}=5 \ne 3+4.\)

The quadratic formula

The quadratic formula

Given the quadratic equation \(ax^2+bx+c=0,\, a,b,\) and \(c\) being real numbers \(a \ne 0\), then
\[x=\frac{-b \pm \sqrt{(b^2-4ac)}}{2a},\]
where \(b^2-4ac\) is called the discriminant.

If the discriminant is \(0\) (that is \(b^2-4ac=0\)) then the quadratic equation has exactly one solution (root) and that solution is \[x=\frac{-b}{2a}.\]

If the discriminant is positive (that is \(b^2-4ac>0\)) then the quadratic equation has two distinct solutions (roots).

If the discriminant is negative (that is \(b^2-4ac<0\)) then the quadratic equation has no real number solutions.

Example \(\PageIndex{9}\):

The quadratic equation \(4x^2-20x+25=0\) has exactly one solution since the discriminant \(= (-20)^2-(4)(4)(25)=400-400=0.\)

In fact, \(x=\displaystyle \frac{-(-20)}{2(4)}=\frac{5}{2}.\)

Example \(\PageIndex{10}\):

Given that \(3x^2+2x-7=0.\) Here \(a=3,b=2,c=-7.\)
\begin{eqnarray}
\mbox{ The discriminant} & =& 2^2-(4)(3)(-7)\nonumber \\
&=& 4+84\nonumber\\
&=& 88.\nonumber
\end{eqnarray}

Since the discriminant is positive, the equation has two distinct real number solutions.
In fact, \begin{eqnarray}
x&=&\frac{-2 \pm \sqrt{88}}{2(3)}\nonumber\\
&=&\frac{2(-1 \pm \sqrt{22})}{2(3)}\nonumber\\
&=&\frac{-1 \pm \sqrt{22}}{3}.\nonumber
\end{eqnarray}

Example \(\PageIndex{11}\):

Given that \(3x^2-2x+7=0.\) Here \(a=3,b=-2,c=7.\)

\begin{eqnarray}
\mbox{ The discriminant} & =& (-2)^2-(4)(3)(7)\nonumber \\
&=& 4-84\nonumber\\
&=& -80<0.\nonumber
\end{eqnarray}

Since the discriminant is negative, the equation has no real number solutions.