3.5E: Exercises
- Page ID
- 10930
This page is a draft and is under active development.
Exercise \(\PageIndex{1}\)
1) If c is a critical point of \(f(x)\), when is there no local maximum or minimum at \(c\)? Explain.
2) For the function \(y=x^3\), is \(x=0\) both an inflection point and a local maximum/minimum?
- Answer
-
It is not a local maximum/minimum because \(f′\) does not change sign
3) For the function \(y=x^3\), is \(x=0\) an inflection point?
4) Is it possible for a point \(c\) to be both an inflection point and a local extrema of a twice differentiable function?
- Answer
-
No
6) Why do you need continuity for the first derivative test? Come up with an example.
7) Explain whether a concave-down function has to cross \(y=0\) for some value of \(x\).
- Answer
-
False; for example, \(y=\sqrt{x}\).
8) Explain whether a polynomial of degree \(2\) can have an inflection point.
- Answer
-
Under Construction.
Exercise \(\PageIndex{2}\)
For the following exercises, analyze the graphs of \(f′\), then list all intervals where f is increasing or decreasing.
1)
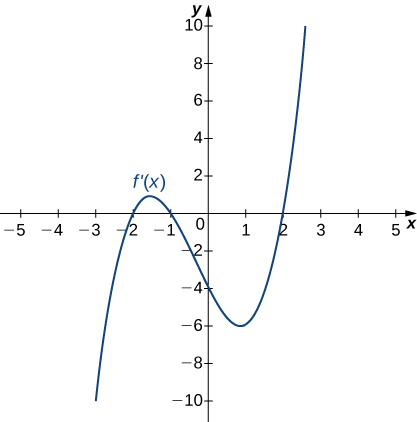
- Answer
-
Increasing for \(−2<x<−1\) and \(x>2\); decreasing for \(x<−2\) and \(−1<x<2\)
2)
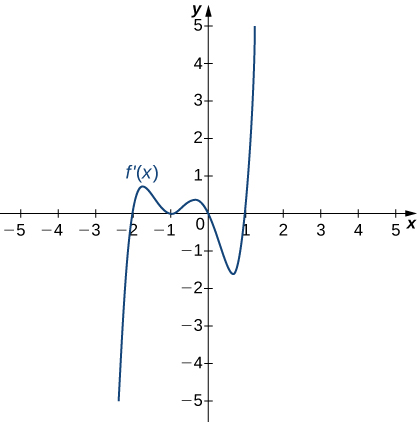
3)
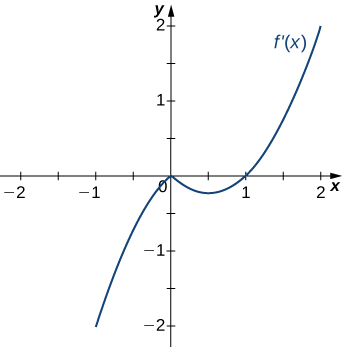
- Answer
-
Decreasing for \(x<1\), increasing for \(x>1\)
4)
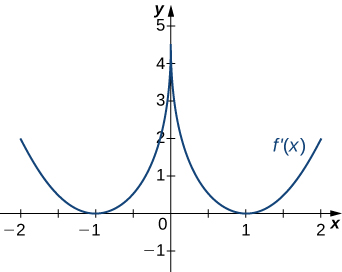
5)
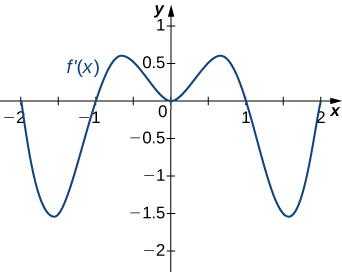
- Answer
-
Decreasing for \(−2<x<−1\) and \(1<x<2\); increasing for \(−1<x<1\) and \(x<−2\) and \(x>2\)
Exercise \(\PageIndex{3}\)
For the following exercises, analyze the graphs of \(f′,\) then list all intervals where
a. \(f\) is increasing and decreasing and
b. the minima and maxima are located.
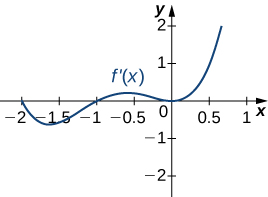
1)
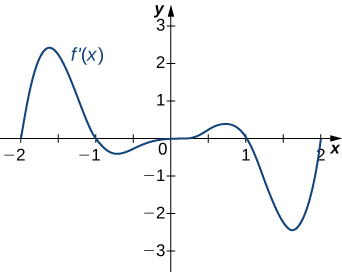
- Answer
-
a. Increasing over \(−2<x<−1,0<x<1,x>2\), decreasing over \(x<−2, −1<x<0,1<x<2;\) b. maxima at \(x=−1\) and \(x=1\), minima at \(x=−2\) and \(x=0\) and \(x=2\)
2)
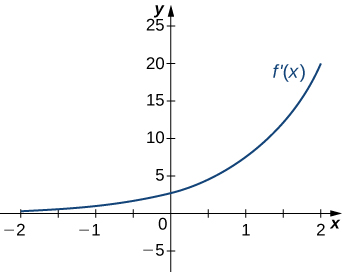
3)
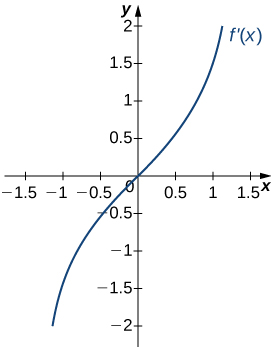
- Answer
-
a. Increasing over \(x>0\), decreasing over \(x<0;\) b. Minimum at \(x=0\)
4)
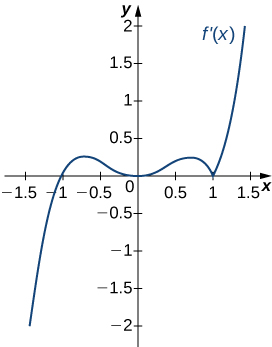
Exercise \(\PageIndex{4}\)
For the following exercises, analyze the graphs of \(f′\), then list all inflection points and intervals \(f\) that are concave up and concave down.
1)
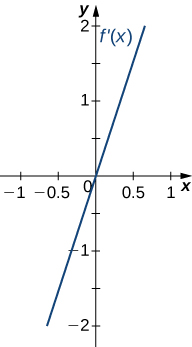
- Answer
-
Concave up on all \(x\), no inflection points
2)
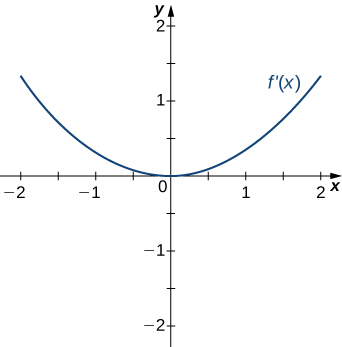
3)
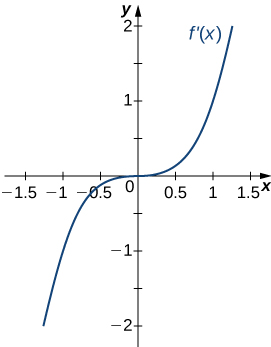
- Answer
-
Concave up on all \(x\), no inflection points
4)
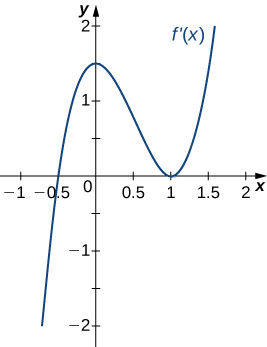
5)
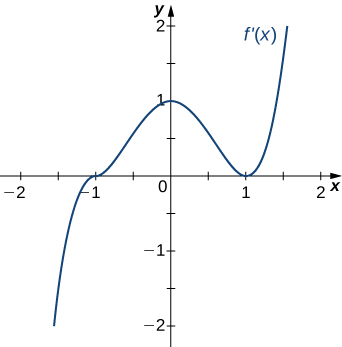
- Answer
-
Concave up for \(x<0\) and \(x>1\), concave down for \(0<x<1\), inflection points at \(x=0\) and \(x=1\)
Exercise \(\PageIndex{5}\)
For the following exercises, draw a graph that satisfies the given specifications for the domain \(x=[−3,3].\) The function does not have to be continuous or differentiable.
1) \(f(x)>0,f′(x)>0\) over \(x>1,−3<x<0,f′(x)=0\) over \(0<x<1\)
2) \(f′(x)>0\) over \(x>2,−3<x<−1,f′(x)<0\) over \(−1<x<2,f''(x)<0\) for all \(x\)
3) \(f''(x)<0\) over \(−1<x<1,f''(x)>0,−3<x<−1,1<x<3,\) local maximum at \(x=0,\) local minima at \(x=±2\)
4) There is a local maximum at \(x=2,\) local minimum at \(x=1,\) and the graph is neither concave up nor concave down.
5) There are local maxima at \(x=±1,\) the function is concave up for all \(x\), and the function remains positive for all \(x.\)
- Answer
-
Under Construction
Exercise \(\PageIndex{6}\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing and
b. local minima and maxima of \(f\).
1) \(f(x)=sinx+sin^3x\) over −π<x<π
- Answer
-
a. Increasing over \(−\frac{π}{2}<x<\frac{π}{2},\) decreasing over \(x<−π\frac{π}{2},x>\frac{π}{2}\)
b. Local maximum at \(x=\frac{π}{2}\); local minimum at \(x=−\frac{π}{2}\)
2) \(f(x)=x^2+cosx\)
- Answer
-
Under Construction
Exercise \(\PageIndex{7}\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f\),
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\)
1) \(f(x)=x^3−4x^2+x+2\)
- Answer
-
a. Concave up for \(x>\frac{4}{3},\) concave down for \(x<\frac{34}{3}\)
b. Inflection point at \(x=\frac{4}{3}\)
2) \(f(x)=x^2−6x\)
3) \(f(x)=x^3−6x^2\)
- Answer
-
a. Increasing over \(x<0\) and \(x>4,\) decreasing over \(0<x<4\)
b. Maximum at \(x=0\), minimum at \(x=4\)
c. Concave up for \(x>2\), concave down for \(x<2\)
d. Infection point at \(x=2\)
4) \(f(x)=x^4−6x^3\)
5) \(f(x)=x^{11}−6x^{10}\)
- Answer
-
a. Increasing over \(x<0\) and \(x>\frac{60}{11}\), decreasing over \(0<x<\frac{60}{11}\)
b. Minimum at \(x=\frac{60}{11}\)
c. Concave down for \(x<\frac{54}{11}\), concave up for \(x>\frac{54}{11}\)
d. Inflection point at \(x=\frac{54}{11}\)
6) \(f(x)=x+x^2−x^3\)
7) \(f(x)=x^2+x+1\)
- Answer
-
a. Increasing over \(x>−\frac{1}{2}\), decreasing over \(x<−\frac{1}{2}\)
b. Minimum at \(x=−\frac{1}{2}\)
c. Concave up for all \(x\)
d. No inflection points
8) \(f(x)=x^3+x^4\)
Exercise \(\PageIndex{8}\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f,\)
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f.\) Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.
1) \(f(x)=sin(πx)−cos(πx)\) over \(x=[−1,1]\)
- Answer
-
a. Increases over \(−\frac{1}{4}<x<\frac{3}{4},\) decreases over \(x>\frac{3}{4}\) and \(x<−\frac{1}{4}\)
b. Minimum at \(x=−\frac{1}{4}\), maximum at \(x=\frac{3}{4}\)
c. Concave up for \(−\frac{3}{4}<x<\frac{1}{4}\), concave down for \(x<−\frac{3}{4}\) and \(x>\frac{1}{4}\)
d. Inflection points at \(x=−\frac{3}{4},x=\frac{1}{4}\)
2) \(f(x)=x+sin(2x)\) over \(x=[−\frac{π}{2},\frac{π}{2}]\)
3) \(f(x)=sinx+tanx\) over \((−\frac{π}{2},\frac{π}{2})\)
- Answer
-
a. Increasing for all \(x\)
b. No local minimum or maximum
c. Concave up for \(x>0\), concave down for \(x<0\)
d. Inflection point at \(x=0\)
4) \(f(x)=(x−2)^2(x−4)^2\)
5) \(f(x)=\frac{1}{1−x},x≠1\)
- Answer
-
a. Increasing for all \(x\) where defined
b. No local minima or maxima
c. Concave up for \(x<1\); concave down for \(x>1\)
d. No inflection points in domain
6) \(f(x)=\frac{sinx}{x}\) over \(x=[−2π,2π] [2π,0)∪(0,2π]\)
7) \(f(x)=sin(x)e^x\) over \(x=[−π,π]\)
- Answer
-
a. Increasing over \(−\frac{π}{4}<x<\frac{3π}{4}\), decreasing over \(x>\frac{3π}{4},x<−\frac{π}{4}\)
b. Minimum at \(x=−\frac{π}{4}\), maximum at \(x=\frac{3π}{4}\)
c. Concave up for \(−\frac{π}{2}<x<\frac{π}{2}\), concave down for \(x<−\frac{π}{2},x>\frac{π}{2}\)
d. Infection points at \(x=±\frac{π}{2}\)
8) \(f(x)=lnx\sqrt{x},x>0\)
9) \(f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},x>0\)
- Answer
-
a. Increasing over \(x>4,\) decreasing over \(0<x<4\)
b. Minimum at \(x=4\)
c. Concave up for \(0<x<8\sqrt[3]{2}\), concave down for \(x>8\sqrt[3]{2}\)
d. Inflection point at \(x=8\sqrt[3]{2}\)
10) \(f(x)=\frac{e^x}{x},x≠0\)
11) \(f(x)=\frac{x}{ln(|x|)}\)
- Answer
-
a. Increasing over \(x>e,\) decreasing over \(-1<x<e\)
b. Minimum at \(x=e\)
c. Concave up for \((-1,0) \cup (1, \infty)\\), concave down for \((0,1)\)
d. Inflection point at \(x=0\)
Exercise \(\PageIndex{9}\)
For the following exercises, interpret the sentences in terms of \(f,f′,\) and \(f''.\)
1) The population is growing more slowly. Here \(f\) is the population.
- Answer
-
\(f>0,f′>0,f''<0\)
2) A bike accelerates faster, but a car goes faster. Here \(f=\) Bike’s position minus Car’s position.
3) The airplane lands smoothly. Here \(f\) is the plane’s altitude.
- Answer
-
\(f>0,f′<0,f''<0\)
4) Stock prices are at their peak. Here \(f\)is the stock price.
5) The economy is picking up speed. Here \(f\) is a measure of the economy, such as GDP.
- Answer
-
\(f>0,f′>0,f''>0\)
Exercise \(\PageIndex{10}\)
For the following exercises, consider a third-degree polynomial \(f(x),\) which has the properties f′(1)=0,f′(3)=0.
Determine whether the following statements are true or false. Justify your answer.
1) \(f(x)=0\) for some \(1≤x≤3\)
2) \(f''(x)=0\) for some \(1≤x≤3\)
- Answer
-
True, by the Mean Value Theorem
3) There is no absolute maximum at \(x=3\)
4) If \(f(x)\) has three roots, then it has \(1\) inflection point.
- Answer
-
True, examine derivative
5) If \(f(x)\) has one inflection point, then it has three real roots.
\begin{enumerate}
\item {Consider the function \[f(x)=x^2 e^{-x}.\]
\begin{enumerate}
\item Find the interval(s) on which $f(x)$ is increasing and
\item Find the interval(s) on which $f(x)$ is decreasing and
\item Find the local (relative) maximum and local (relative) minimum (if any).
%\vspace{8in}
\end{enumerate}}
\item {Consider the function \[f(x)=3(x^2-4)^{2/3}.\]
\begin{enumerate}
\item Find the interval(s) on which $f(x)$ is increasing and
\item Find the interval(s) on which $f(x)$ is decreasing and
\item Find the local (relative) maximum and local (relative) minimum (if any).
%\vspace{8in}
\end{enumerate}}
\item Consider the function \[g(x)=10x^3+ 3x^5.\[ Find
\begin{enumerate}
\item the interval(s) on which $g(x)$ is concave up and
\item the interval(s) on which $g(x)$ is concave down and
\item inflection points ( if any).
\end{enumerate}
\item Consider the function \[g(x)=e^{-x^2/2}.\[ Find
\begin{enumerate}
\item the interval(s) on which $g(x)$ is concave up and
\item the interval(s) on which $g(x)$ is concave down and
\item inflection points ( if any).
\end{enumerate}
\item{ Find horizontal asymptote of the function \[ y=f(x)= x- \sqrt{x^2+2x-6}.\[}
%\vspace{8 in}
\item { Consider the function \[f(x)=x e^{-2x}.\]
\begin{enumerate}
\item Find the interval(s) on which $f(x)$ is increasing and
\item Find the interval(s) on which $f(x)$ is decreasing and
\item Find the local (relative) maximum and local (relative) minimum (if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function \[f(x)=x^2 e^{-x}.\]
\begin{enumerate}
\item Find the interval(s) on which $f(x)$ is increasing and
\item Find the interval(s) on which $f(x)$ is decreasing and
\item Find the local (relative) maximum and local (relative) minimum (if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function \[f(x)=x+\frac{1}{x}.\]
\begin{enumerate}
\item Find the interval(s) on which $f(x)$ is increasing and
\item Find the interval(s) on which $f(x)$ is decreasing and
\item Find the local (relative) maximum and local (relative) minimum (if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function \[g(x)=5x^3+ 2x^5.\[ Find
\begin{enumerate}
\item the interval(s) on which $g(x)$ is concave up and
\item the interval(s) on which $g(x)$ is concave down and
\item inflection points ( if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function \[g(x)=\ln(1+x^2).\[ Find
\begin{enumerate}
\item the interval(s) on which $g(x)$ is concave up and
\item the interval(s) on which $g(x)$ is concave down and
\item inflection points ( if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function \[g(x)=(3-x^2)^2.\[ Find
\begin{enumerate}
\item the interval(s) on which $g(x)$ is concave up and
\item the interval(s) on which $g(x)$ is concave down and
\item inflection points ( if any).
%\vspace{8in}
\end{enumerate}}
\item { Consider the function
\]
\displaystyle{f(t)=\frac{1}{1-t^2}}
\]
b) Find vertical and horizontal asymptotes (if any).
c) Find the intervals when $f(t)$ is concave up and concave down.
}
\item {Consider the function
\]
\displaystyle{f(t)=e^{-t^2}}
\]
a) Find the local maxima and minima for the function $f(t)$.
b) Find the intervals when $f(t)$ is increasing and decreasing.
c) Find the intervals when $f(t)$ is concave up and down.
d) Find the inflection points for $f(t)$.
}
\item { Find all vertical and
horizontal asymptotes for the function
\]
\displaystyle{f(x)=\frac{x^2-5x+6}{x^2-4x+3}}
\]
Justify your work using limits.
}
\item Suppose we have the following
information, where
\[y=\frac{x}{x^2-1},\qquad y^\prime=-\frac{x^2+1}{\left(x^2-1\right)^2},
\mbox{ and }y^{\prime\prime}=\frac{2x\left(x^2+3\right)}{\left(x^2-1
\right)^3}.\]
\noindent a) Identify any asymptotes for the function $y$ using limits.
\noindent b) Find where the function $y$ is
increasing/decreasing and any relative extrema.
\noindent c) Find where the function $y$ is concave
up/down and any points of inflection.
\noindent d) Graph the function $y$.
\item Let $f(x) = x^{5/4}-x^{1/4}.$ Determine the intervals on which $f$ is increasing and decreasing and find any local extrema.
\item Let $g(x) = \ln (x^2+1).$ Determine the intervals of concavity of $g(x)$ and locate any inflection points. \item Let $f(x) = x^2e^{-16x^2}.$ Determine the intervals on which $f$ is increasing and decreasing and find any local extrema.
\item Let $g(x) = (\ln x)^2.$ Determine the intervals of concavity of $g(x)$ and locate any inflection points. \item Given a function $\displaystyle{y=f(x)= x-2tan^{-1}(x)}$, find interval(s) on which the function is concave
up and the interval(s) on which the function is concave down, and inflection point(s).
\item Let $g(x) = x-2 \tan^{-1}(x).$ Determine the intervals of concavity of $g(x)$ and locate any inflection points.
\end{enumerate}
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

