2.6: Division Algorithm
- Page ID
- 7554
This page is a draft and is under active development.
The absolute value
Definition: Absolute value
For any real number \(x\) the absolute value of \(x\) is denoted by \(|x|\) and defined by
\[|x|= \left\{\begin{array}{cc}
x& \mbox{ if } x\geq 0,\\
-x& \mbox{ if } x< 0.
\end{array}
\right.\]
Example \(\PageIndex{1}\) : Absolute Value
Consequently we see that \(|-2|=|2|=2.\)

Theorem \(\PageIndex{1}\): Well ordering principle
Every non-empty subset of \(\bf N\) has a smallest element.
Theorem \(\PageIndex{2}\): Division Algorithm
Let \(n\) and \(d\) be integers. Then there exist unique integers \(q\) and \(r\) such that \(n=dq+r, 0\leq r <|d|\), where \(q\) is the quotient and \(r\) is the remainder, and the absolute value of \(d\) is defined as:
\[|d|= \left\{ \begin{array}{c}
d, \mbox{if } d \geq 0\\
\\
-d, \mbox{if } d<0.
\end{array}
\right.\]
- Proof
-
We will show that \(q,r \in \mathbb{Z}\) exist and that they are unique.
Let \(a,b \in \mathbb{Z}\) s.t. \(b>0\).
Let \(S\) be a set defined by \(S=\{a-bm: a-bm \ge 0, m\in \mathbb{Z}\}\).
We will show existence by examining the possible cases.
Case 1: \( 0 \in S\)
If \(0 \in S\), then \(a-bm=0\) for some \(m \in \mathbb{Z}\).
Thus, \(a=bm\)
Since \(b|a\), \(q=m\) and \(r=0\).
Therefore existence has been proved.
Case 2: \(0 \notin S\).
Since \(0 \notin S\), we will show that \(S \ne \emptyset\) by examining the possible cases. Note: \(S \subseteq \mathbb{N}\).
Case a: \(a>0\).
Since \(a>0\), \(a=a-b(0)>0\).
Therefore \(a \in S\).
Case b: \(a<0\).
Consider \(a-bm\), where \(m=2a\).
Thus \(a-b(2a)=a(1-2b)\).
Consider \(1-2b\) is always negative since \(b>0 \cap b \in \mathbb{N}\), thus greatest \(1-2b\) can be in \(-1\).
Therefore \(a(1-2b) \ge 0\) since \(b \ge 1\).
Note: The \(\ge\) could be > without loss of generality.
Since both case a & b are non empty sets, \(S \ne \emptyset \subseteq \mathbb{N}\).
Thus \(S\) has the smallest element by the well ordering principle and lets call it \(r\).
That means \(r=a-bm\), for some \(m\in \mathbb{Z}\) where \(r \ge 0\).
Thus the non empty set is \(r=a-bm \ge 0\).
We shall show that \(r < b\) by proceeding with a proof by contradiction.
Assume that \(r \ge b\).
Then \( a-b(m+1)=a-bm-b=r-b \ge 0\) for some \(m \in \mathbb{Z}\).
Then \(r-b \in S\) and \(r-b<r\). Note \((b>0)\)
This contradicts that \(r\) is the smallest element of \(S\).
Therefore \(r < b\).
Having examined all possible cases, \(a=bq+r, 0 \le r < b\) exists.
Next, we will show uniqueness.
Let \(r_1,r_2, q_1,q_2\) s.t. \(a=bq_1+r_1\) and \(a=bq_2+r_2\) with \( 0 \le r_1,r_2 < b\).
Consider \(bq_1+r_1=bq_2+r_2\), \(0 \le r_1<b\).
Further since \(b(q_1-q_2)=r_2-r_1\), \(b|(r_2-r_1)}\), but \(b\) has to be \(\le r_1\).
Since, \(r_2-r_1 < b\), \(r_2-r_1=0\) and \(r_1=r_2\).
Hence \(q_1=q_2\).
Therefore uniqueness has been shown.
Let \(n\) and \(d\) be integers. Then there exist unique integers \(q\) and \(r\) such that \(n=dq+r, 0\leq r <|d|\), where \(q\) is the quotient and \(r\) is the remainder, and the absolute value of \(d\) is defined as:
\[|d|= \left\{ \begin{array}{c}
d, \mbox{if } d \geq 0\\
\\
-d, \mbox{if } d<0.
\end{array}
\right.\]
Example \(\PageIndex{2}\):
Find the \(q\) is the quotient and \(r\) is the remainder for the following values of \(n\) and \(d\).
- \(n=2018\) and \(d=343\).
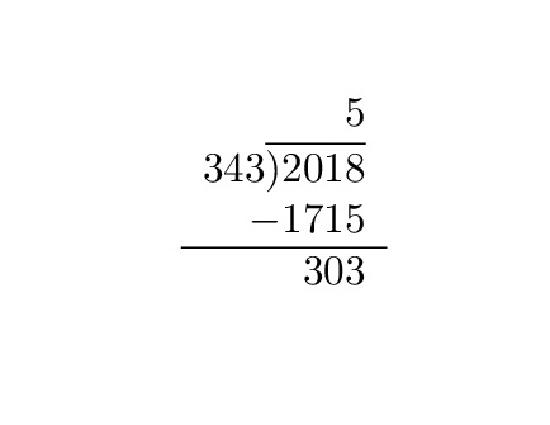
Thus \(2018=(5)(343)+303\).
2. \(n=-2018\) and \(d=343\).
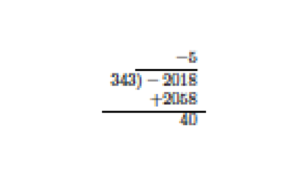
Thus \(-2018=(-6)(343)+40\).-
3, . \(n=2018\) and \(d=-343\).
Thus \(2018=(6)(-343)+40\).
4.
\(n=-2018\) and \(d=-343\).
Thus \(-2018=(6)(-343)+ 40\).
Example \(\PageIndex{3}\):
Today is March 3, 2018, and it is Friday. What day will it be on March 3, 2019?
At first, note that 2019 is not a leap year. Therefore, there are \(365\) days between March 3, 2018, and March 3, 2019. Also \(365=(52)(7)+1\). There are seven days in a week and keeping Friday as 0, we can conclude that March 3, 2019, will be a Saturday.
Leap Year
The Gregorian calendar is the calendar we most commonly use today throughout the world. The Gregorian calendar consists of both common years with 365 days and Leap years consisting of 366 days due to the intercalary day added on February 29th.Leap years are necessary in order to keep the Gregorian calendar aligned with the Earth’s revolution around the sun.
Following our modern day Gregorian calendar there are three rules to take into consideration to identify leap years:
- The year must be evenly divided by 4.
- If the year is evenly divided by 100, it is not a leap year unless:
- The year is also evenly divided by 400.
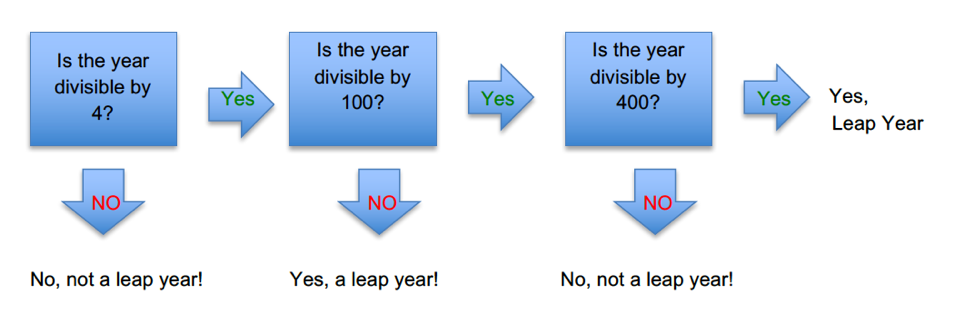
For example: the years 1600, 1800, 2000 are all leap years, but the years 1700 and 1900 aren’t leap years.
Example \(\PageIndex{4}\):
Each day, Ms. Mary visits grocery stores A, B, C, D in that order. Further, she spends exactly \( \$ 27, \$ 35, \$ 12, \$ 40\) in the stores A, B, C, D respectively. Her total expenditure, from the beginning of the month up to a certain day of the month, was \(\$924\). Which store would she be visiting next?
Example \(\PageIndex{5}\)
In a 101-digit multiple of 13, the first 50 digits are all 5s and the last 50 digits are all 8s. What is the middle digit?
Solution
Since \( 13 | 555555 \) and \( 13 | 888888,\) we need to consider what the value of \( X \in ℤ\) is such that \(13 | 55X88 \), since
the first and last \(48\) digits of the number will produce multiples of \(13. \) At this point (Solution 1), trial and error can be applied to this calculation, resulting in X = 5.
A more elegant solution (Solution 2) can be obtained by recognizing that any number \( Q ∈ ℤ+ \) can be written as:
\( Q = 10a + b, \) where \( a, b ∈ \{0, 1, ..., 8, 9\}. \)
Next find a multiple of \(13\) that has a \(1 \) as the last digit. This condition is satisfied with \(91\). Next, rewrite the equation to be \(Q - 91b = 10a + b - 91b \) and simplify to \(Q - 91b = 10(a - 9b). \) Using this formula, \(55X8 - 9(8)\) a number whose last digit is a \(6\), is divisible by \(13 \) and the first two digits must be either \(55 \) or \(54 \) will satisfy the condition \( 13 | 55X88.\) The only number that satisfies these conditions is \(5486. \) Adding back \(72,\) we obtain \(5558,\) thus confirming that \(X = 5.\)
A more deductive solution (Solution 3) can be seen using long division as follows:



