1.3: Trigonometric Functions
- Page ID
- 8213
When you first encountered the trigonometric functions it was probably in the context of "triangle trigonometry,'' defining, for example, the sine of an angle as the "side opposite over the hypotenuse.'' While this will still be useful in an informal way, we need to use a more expansive definition of the trigonometric functions. First an important note: while degree measure of angles is sometimes convenient because it is so familiar, it turns out to be ill-suited to mathematical calculation, so (almost) everything we do will be in terms of radian measure of angles.
To define the radian measurement system, we consider the unit circle in the \(xy\)-plane:
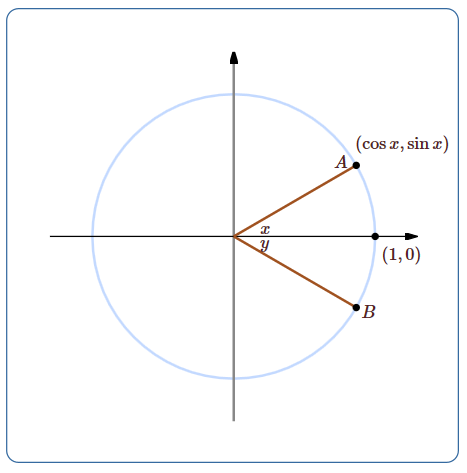
While an angle with a particular measure can appear anywhere around the circle, we need a fixed, conventional location so that we can use the coordinate system to define properties of the angle. The standard convention is to place the starting radius for the angle on the positive \(x\)-axis, and to measure positive angles counterclockwise around the circle. In the figure, \(x\) is the standard location of the angle \(\pi/6\), that is, the length of the arc from \((1,0)\) to \(A\) is \(\pi/6\). The angle \(y\) in the picture is \(-\pi/6\), because the distance from \((1,0)\) to \(B\) along the circle is also \(\pi/6\), but in a clockwise direction.
Now the fundamental trigonometric definitions are: the cosine of \(x\) and the sine of \(x\) are the first and second coordinates of the point \(A\), as indicated in the figure. The angle \(x\) shown can be viewed as an angle of a right triangle, meaning the usual triangle definitions of the sine and cosine also make sense. Since the hypotenuse of the triangle is 1, the "side opposite over hypotenuse'' definition of the sine is the second coordinate of point \(A\) over 1, which is just the second coordinate; in other words, both methods give the same value for the sine.
The simple triangle definitions work only for angles that can "fit'' in a right triangle, namely, angles between 0 and \(\pi/2\). The coordinate definitions, on the other hand, apply to any angles, as indicated in this figure:
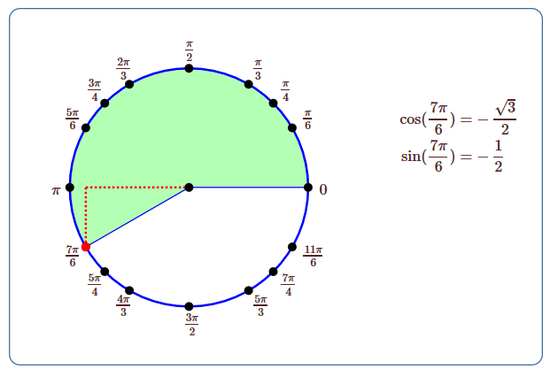
The angle \(x\) is subtended by the heavy arc in the figure, that is, \(x=7\pi/6\). Both coordinates of point \(A\) in this figure are negative, so the sine and cosine of \(7\pi/6\) are both negative.
The remaining trigonometric functions can be most easily defined in terms of the sine and cosine, as usual:
\[\eqalign{ \tan x &= {\sin x\over \cos x}\cr \cot x &= {\cos x \over \sin x}\cr \sec x &= {1\over \cos x}\cr \csc x &= {1\over \sin x}\cr }\]
and they can also be defined as the corresponding ratios of coordinates.
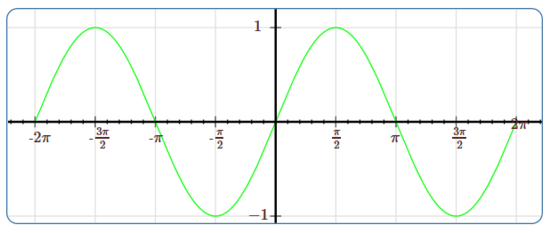
Although the trigonometric functions are defined in terms of the unit circle, the unit circle diagram is not what we normally consider the graph of a trigonometric function. (The unit circle is the graph of, well, the circle.) We can easily get a qualitatively correct idea of the graphs of the trigonometric functions from the unit circle diagram. Consider the sine function, \(y=\sin x\). As \(x\) increases from 0 in the unit circle diagram, the second coordinate of the point \(A\) goes from 0 to a maximum of 1, then back to 0, then to a minimum of \(-1\), then back to 0, and then it obviously repeats itself. So the graph of \(y=\sin x\) must look something like this: