Derivatives The Easy Way
- Page ID
- 623
Constant Rule and Power Rule
We have seen the following derivatives:
- If f(x) = c, then f '(x) = 0
- If f(x) = x, then f '(x) = 1
- If f(x) = x2, then f '(x) = 2x
- If f(x) = x3, then f '(x) = 3x2
- Iff(x) = x4, thenf '(x) = 4x3
This leads us the guess the following theorem.
|
Theorem d |
Proof:
We have
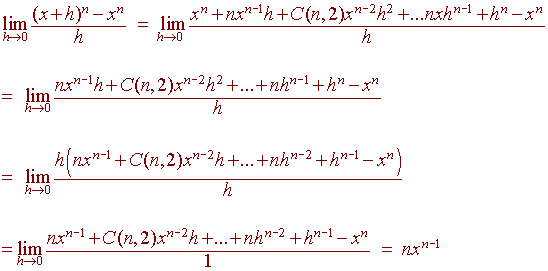
Applications
Example
Find the derivatives of the following functions:
-
f(x) = 4x3 - 2x100
-
f(x) = 3x5 + 4x8 - x + 2
-
f(x) = (x3 - 2)2
Solution
We use our new derivative rules to find
-
12x2 - 200x99
-
15x3+32x7-1
-
First we FOIL to get
[x6 - 4x3 + 4] '
Now use the derivative rule for powers
6x5 - 12x2
Example:
Find the equation to the tangent line to
y = 3x3 - x + 4
at the point(1,6)
Solution:
y' = 9x2 - 1
at x = 1 this is 8. Using the point-slope equation for the line gives
y - 6 = 8(x - 1)
or
y = 8x - 2
Example:
Find the points where the tangent line to
y = x3 - 3x2 - 24x + 3
is horizontal.
Solution:
We find
y' = 3x2 - 6x - 24
The tangent line will be horizontal when its slope is zero, that is, the derivative is zero. Setting the derivative equal to zero gives:
3x2 - 6x - 24 = 0
or
x2 - 2x - 8 = 0
or
(x - 4)(x + 2) = 0
so that
x = 4 or x = -2
Derivative of f(x) = sin(x)
Proof:
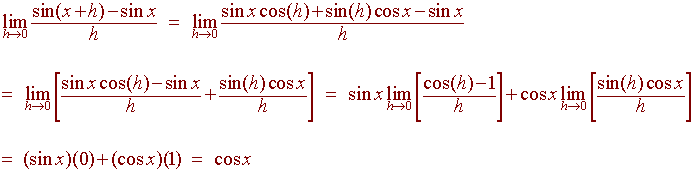
d/dx cos(x)


