15.7: Triple Integrals in Cylindrical and Spherical Coordinates
- Page ID
- 2649
Sometimes, you may end up having to calculate the volume of shapes that have cylindrical, conical, or spherical shapes and rather than evaluating such triple integrals in Cartesian coordinates, you can simplify the integrals by transforming the coordinates to cylindrical or spherical coordinates. For this topic, we will learn how to do such transformations then evaluate the triple integrals.
Introduction
As you learned in Triple Integrals in Rectangular Coordinates, triple integrals have three components, traditionally called x, y, and z. When transforming from Cartesian coordinates to cylindrical or spherical or vice versa, you must convert each component to their corresponding component in the other coordinate system.
There are three coordinate systems that we will be considering. The first is the traditional x, y, and z system also know as the Cartesian coordinate the system; the other two are explored below.
Converting to Cylindrical Coordinates
The second set of coordinates is known as cylindrical coordinates. Working in cylindrical coordinates is essentialy the same as working in polar coordinates in two dimensions except we must account for the z-component of the system. When transforming from Cartesian to cylindircal, x and y become their polar counterparts. Recall that \(x=r*cos \theta\), \(y=r*sin \theta\), \(r^2=x^2+y^2\), and \(tan\theta=\dfrac{y}{x}\). Now, the conversion for z is simply \(z=z\). \(r\) and \(\theta\) create a plane parallel to the xy-plane, and adding the z component simply gives the plane a "height".
Now, say we have the equation \(r=1\) for \(0\leq\theta<2\pi\). In two dimensions, that would simply give us a circle centered at \((0,0)\) with a radius of 1. By adding the z-axis, the circle has a height of z, which gives it the shape of a cylinder, hence the name cylindrical coordinates.
As seen in Double Integrals in Polar Form, when converting a double integral from Cartesian to polar coordinates, the \(dA\) term, \(dx\,dy\) in Cartesian gets converted to its polar equivilent.
\[\iint_{D}f(x,y) dxdxy \Rightarrow \iint_{D}f(r\cos \theta ,r\sin \theta) rd\,r\,d\theta\nonumber \]
The same conversion happens with triple integrals from Cartesian to cylindrical for the \(dV\) term except you must account for the z-axis with a \(dz\) term.
\[\iiint_{D}f(x,y,z) dxdydz \Rightarrow \iiint_{D}f(r\cos \theta ,r\sin \theta ,z) r\,dr\,d\theta \;dz\nonumber \]
Example \(\PageIndex{1}\): Using Cylindrical Coordinates
Convert this triple integral into cylindrical coordinates and evaluate
\[\int_{-1}^{1}\int_{0}^{\sqrt{1-x^2}}\int_{0}^{y}x^2dz\; dy\; dx \nonumber\nonumber \]
Solution
There are three steps that must be done in order to properly convert a triple integral into cylindrical coordinates.
First, we must convert the bounds from Cartesian to cylindrical. By looking at the order of integration, we know that the bounds really look like
\[\int_{x=-1}^{x=1}\int_{y=0}^{y=\sqrt{1-x^2}}\int_{z=0}^{z=y} \nonumber \nonumber \]
Using the Cartesian to cylindrical conversions, we see that the new bounds are
\[\int_{x=-1}^{x=1}\int_{y=0}^{y=\sqrt{1-x^2}}\int_{z=0}^{z=y} \Rightarrow \int_{\theta=0}^{\theta=\pi}\int_{r=0}^{r=1}\int_{z=0}^{z=r\sin\theta} \nonumber \nonumber \]
Next, we convert the integrand to its cylindrical equivalent
\[x^2 \Rightarrow r^2cos\theta \nonumber \nonumber \]
Thirdly, we convert the differentials at the end of the integral to their cylindrical equivalent being careful to denote the correct order of integration
\[dz\,dy\,dx \Rightarrow r\, dz\, dr\, d\theta \nonumber \nonumber \]
Finally, we put it all together, and we have our newly cylindrically-converted integral
\[\int_{0}^{\pi}\int_{0}^{1}\int_{0}^{r \sin\theta}r^2\cos^2\theta r\,dz \,dr \, d\theta \nonumber \nonumber \]
Now, we actually evaluate the integral
\[\begin{align*} &\int_{0}^{\pi}\int_{0}^{1}\int_{0}^{r\sin\theta}r^3\cos^2\theta dz\, dr\, d\theta \nonumber \\ &= \int_{0}^{\pi}\int_{0}^{1} \left [r^3 \cos^2\theta*z \right]_{z=0}^{z=r\sin\theta} dr\, d\theta \nonumber \\ &= \int_{0}^{\pi}\int_{0}^{1} r^4 \cos^2\theta \sin \, \theta dr\, d\theta \nonumber \\ &= \int_{0}^{\pi} \left[\dfrac{r^5}{5}\cos^2\theta \sin\theta \right]_{r=0}^{r=1} d\theta \nonumber \\ &= \dfrac{1}{5}\int_{0}^{\pi}cos^2\theta \sin\theta d\theta \nonumber \end{align*}\nonumber \]
Using u-substitution, we find that the integrand \(\cos^2\theta \sin \theta\) integrates to
\[\dfrac{1}{5} \left[-\dfrac{1}{3}\cos^3\theta \right]_{\theta=0}^{\theta=\pi} \nonumber \nonumber \]
Which evaluates to
\[\dfrac{1}{5} \left[-\dfrac{1}{3}\cos^3(\pi)+\dfrac{1}{3}\cos^3(0) \right] = \dfrac{2}{15} \nonumber \nonumber \]
Converting to Spherical Coordinates
Figure 1 shows a visual representation of spherical coordinates. We define \(\rho\) as the distance from the origin to point \(P\). The point \(P\) and the origin create a line segment we will call \(\bar{OP}\), \(O\) being the origin. \(\theta\) is the angle in the x-y plane from the projection of \(\bar{OP}\), which is shown as \(\bar{OQ}\). \(\phi\) is the angle between the z-axis and \(\bar{OP}\).
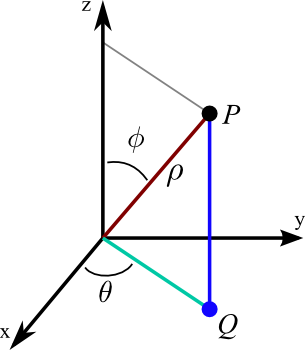
The conversions of Cartesian to Spherical are as follows
Just as \(r=\sqrt{x^2+y^2}\), \(\rho=\sqrt{x^2+y^2+z^2}\) and like with cylindrical, \(\theta=tan^{-1}(\dfrac{y}{x})\)
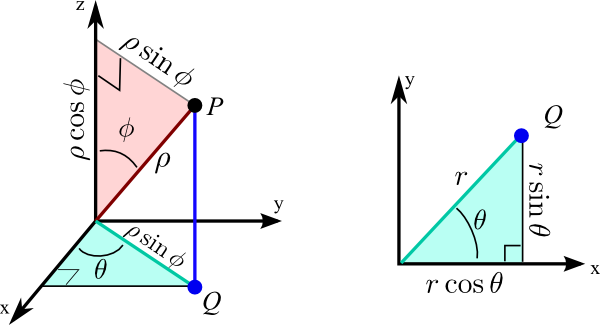
As you can see from Figure 2, \(r=\rho sin\phi\), and using this and other trigonometric relations visible here, we can find conversions for x, y, and z.
x and y look like their cylindrical counterparts; however \(r\) is replaced with \(\rho sin\phi\). So \(x=\rho \sin\phi cos\theta\) and \(y=\rho \sin\phi \sin\theta\). Also, from the diagrams, we see that \(z=\rho cos\phi\).
As for the \(dV\) term of a triple integral, when converted to spherical coordinates, it becomes \(dV=\rho^2 \sin\phi d\rho d\phi d\theta\).
Example \(\PageIndex{2}\): Using Spherical Coordinates
We are going to find the volume between the sphere \(\rho=cos\phi\) and the hemisphere \(\rho=6\). A diagram of the shapes is on the right.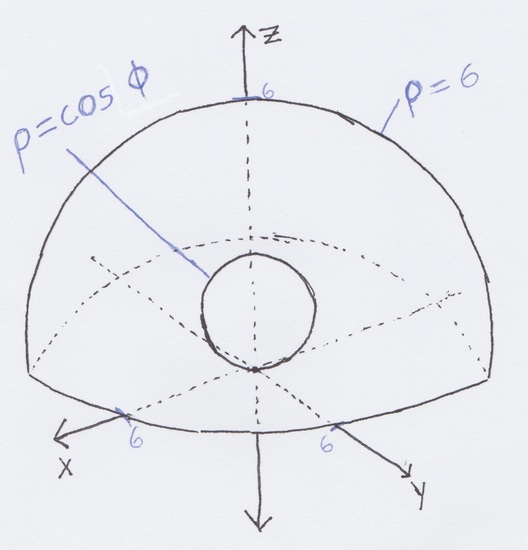
Solution
First we must set up an integral to calculate the volume:
\[V=\int_{\theta_0}^{\theta_1}\int_{\phi_0}^{\phi_1}\int_{\rho_0}^{\rho_1}dV\nonumber \]
Now we replace the \(dV\) term and fill in the bounds of integration:
\[V=\int_{\theta_0=0}^{\theta_1=2\pi}\int_{\phi_0=0}^{\phi_1=\dfrac{\pi}{2}}\int_{\rho_0=cos\phi}^{\rho_1=6}\rho^2 \sin\phi d\rho d\phi d\theta\nonumber \]
From there we evaluate the integral:
\[\begin{align*} V&=\dfrac{1}{3}\int_{0}^{2\pi}\int_{0}^{\dfrac{\pi}{2}} \left(216-cos^3\phi \right) \sin \phi d\phi d\theta \\ & =\dfrac{1}{3}\int_{0}^{2\pi}[-216 \cos\phi+\dfrac{ \cos^4\phi}{4}]^{\dfrac{\pi}{2}}_{0} d\theta \\ & =\dfrac{1}{3}\int_{0}^{2\pi} \left(216-\dfrac{1}{4} \right) d\theta \\ & \dfrac{863}{4}(2\pi) \\ & \dfrac{863\pi}{2} \end{align*}\nonumber \]
Example \(\PageIndex{3}\)
Michael wants to eat a bowl of Fruity Hoops Cereal. However, he needs to go to the store and get milk for his cereal, and he is unsure of how much milk to buy. He needs your help deciding the appropriate amount to purchase. The volume of his cereal bowl can be represented by the region bounded below by \(\rho=4\cos\phi\) and bounded above by \(z=4\). Using this information, find how much milk Michael will need to fill his cereal bowl. The units are in ounces.
First off, we want to draw a diagram, representing the situation, in order to assist us with choosing our bounds of integration.
Contributors and Attributions
- Paul Salessi (UCD)

