1.3: Find the Equation of a Line

Learning Objectives

By the end of this section, you will be able to:

• Find an equation of the line given the slope and \(y\)-intercept
• Find an equation of the line given the slope and a point
• Find an equation of the line given two points
• Find an equation of a line parallel to a given line
• Find an equation of a line perpendicular to a given line

Be Prepared

Before you get started, take this readiness quiz.

1. Solve \(\dfrac{2}{5}(x+15)\).
2. Simplify \(−3(x−(−2))\).
3. Solve for \(y\): \(y−3=−2(x+1)\).

How do online companies know that “we may also like” a particular item based on something we just ordered? How can economists know how a rise in the minimum wage will affect the unemployment rate? How do medical researchers create drugs to target cancer cells? How can traffic engineers predict the effect on our commuting time of an increase or decrease in gas prices? It’s all mathematics.

The physical sciences, social sciences, and the business world are full of situations that can be modeled with linear equations relating two variables. To create a mathematical model of a linear relation between two variables, we must be able to find an equation of a line. In this section, we will look at several ways to write an equation of a line. The specific method we use will be determined by what information we are given.

Find an Equation of a Line Given the Slope and \(y\)-intercept

If we have an equation of a line which is in slope-intercept form, \(y=mx+b\), we can easily determine the line's slope and \(y\)-intercept. Now we will do the reverse - we will start with the slope and the \(y\)-intercept and find an equation of the line. A line has only one equation which is in slope-intercept form. So, if an equation is requested to be in slope-intercept form, we will write "the equation" instead of "an equation".

Example \(\PageIndex{1}\)

Find the slope-intercept form of an equation of a line with slope \(−9\) and \(y\)-intercept \((0,−4)\).

Solution

Since we are given the slope and \(y\)-intercept of the line, we can substitute the needed values into the slope-intercept form, \(y=mx+b.\)

Identify the slope \(m\).	\(m=-9\)
Identify the \(y\)-intercept \((0,b)\) and \(b\).	The \(y\)-intercept is \((0,-4)\), so \(b=-4\).
Substitute the values into \(y=mx+b\).	\(\begin{aligned} y &=mx+b \\ y&=-9x+(-4)\end{aligned}\)
Simplify.	\(y=-9x-4\)
Answer the question in slope-intercept form.	The equation of the line is \(y=-9x-4\).

Try It \(\PageIndex{2}\)

Find the slope-intercept form of an equation of a line with slope \(\dfrac{2}{5}\) and \(y\)-intercept \((0,4)\).

Answer

The equation of the line is \(y=\dfrac{2}{5}x+4\).

Try It \(\PageIndex{3}\)

Find the slope-intercept form of an equation of a line with slope \(−1\) and \(y\)-intercept \((0,−3)\).

Answer

The equation of the line is \(y=−x−3\).

Sometimes, the slope and intercept need to be determined from the graph.

Example \(\PageIndex{4}\)

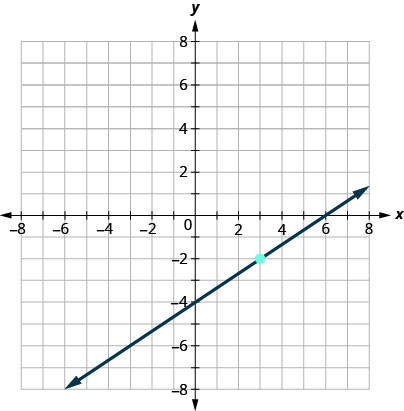
Find the slope-intercept form of an equation of the line shown in the graph.

Solution

We need to find the slope and \(y\)-intercept of the line from the graph so that we can substitute the needed values into the slope-intercept form, \(y=mx+b\).

To find the slope, we choose two points on the graph.

The \(y\)-intercept is \((0,−4)\) and the graph passes through \((3,−2)\).

Pick two points on the line.	\((0,−4)\) and \((3,−2)\)
Determine the rise and run.	The rise is \(2\), and the run is \(3\).
Substitute the rise and run into the slope formula, \(m=\dfrac{\text{rise}}{\text{run}}\).	\(\begin{aligned} m&=\dfrac{\text{rise}}{\text{run}} \\ m&=\dfrac{2}{3}\end{aligned}\)
Find the \(y\)-intercept.	The \(y\)-intercept is \((0,-4)\).
Substitute the values into \(y=mx+b\).	\(\begin{aligned} y&=mx+b\\ y&=\dfrac{2}{3}x+(-4)\end{aligned}\)
Simplify.	\(y=\dfrac{2}{3}x-4\)
Answer the question.	The equation of the line is \(y=\dfrac{2}{3}x-4\).

Try It \(\PageIndex{5}\)

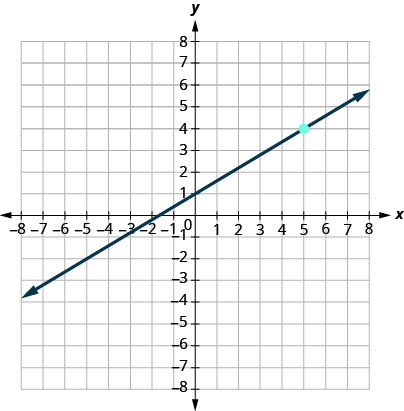
Find the slope-intercept form of an equation of the line shown in the graph.

Answer

The equation of the line is \(y=\dfrac{3}{5}x+1\).

Try It \(\PageIndex{6}\)

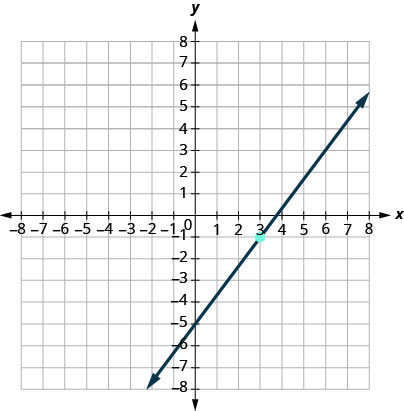
Find the slope-intercept form of an equation of the line shown in the graph.

Answer

The equation of the line is \(y=\dfrac{4}{3}x−5\).

Find an Equation of the Line Given the Slope and a Point

Finding an equation of a line using the slope-intercept form of the equation works well when we are given the slope and \(y\)-intercept or when we read them off a graph. But what happens when we have another point instead of the \(y\)-intercept?

We are going to use the slope formula to derive another form of an equation of the line. By 'another form' we mean that it is an equation that has the line as it's graph though the equation has a different structure, or looks different, from what we have seen before.

Suppose we have a line that has slope \(m\) and that contains some specific point \((x_1,y_1)\) and some other point, which we will just call \((x,y)\). We can write the slope of this line and then change it to a different form. We will write our answer in slope-intercept form, or of the form \(x=a\), since this gives a unique answer.

Write the slope formula based on two points, \((x_1,y_1)\) and \((x,y)\).	\(m=\dfrac{y-y_1}{x-x_1}\)
Multiply both sides of the equation by \(x−x_1\).	\(m(x-x_1)=\left(\dfrac{y-y_1}{x-x_1}\right)\cdot (x-x_1)\)
Simplify.	\(m(x-x_1) = y-y_1\)
Rewrite the equation with the \(y\) terms on the left.	\(y-y_1= m(x-x_1)\) This format is called the point-slope form of an equation of a line.

Point-slope form of an equation of a line

The point-slope form of an equation of a line with slope \(m\) and containing the point \((x_1,y_1)\) is

\[y−y_1=m(x−x_1). \nonumber\]

We can use the point-slope form of an equation to find an equation of a line when we know the slope and at least one point.

How to Find an Equation of a Line Given a Point and the Slope

In the example below we will find an equation for a line with given attributes. In order to have a unique answer, we specify that the answer should be the equation which is in slope-intercept form, or in the form \(x=a\).

Example \(\PageIndex{7}\)

Find an equation of a line with slope \(m=−\dfrac{1}{3}\) that contains the point \((6,−4)\). Write the equation in slope-intercept form.

Solution

In order to use the point-slope form, we need the slope and one point.

Identify the slope.	\(m=−\dfrac{1}{3}\)
Identify the point, \((x_1,y_1)\).	\(\underbrace{(6,−4)}_{(x_1,y_1)}\)
Substitute the values into the point-slope form, \(y-y_1=m(x-x_1)\).	\(\begin{aligned} y-y_1&=m(x-x_1) \\y-(-4)& = −\dfrac{1}{3}(x-6)\end{aligned}\)
Simplify.	\(y+4=-\dfrac{1}{3}x+2\)
Write the equation in slope-intercept form, \(y=mx+b\).	\(y=-\dfrac{1}{3}x-2\)
Answer the question in slope-intercept form, or in the form \(x=a\).	The equation of the line is \(y=-\dfrac{1}{3}x-2\).

Try It \(\PageIndex{8}\)

Find an equation of a line with slope \(m=−\dfrac{2}{5}\) that contains the point \((10,−5)\).

Answer

The equation of the line in slope-intercept form is \(y=−\dfrac{2}{5}x−1\).

Try It \(\PageIndex{9}\)

Find the equation of a line with slope \(m=−\dfrac{3}{4}\) that contains the point \((4,−7)\).

Answer

The equation of the line in slope-intercept form is \(y=−\dfrac{3}{4}x−4\).

We list the steps for easy reference.

To find an equation of a line given the slope and a point

1. Identify the slope.
2. Identify the point.
3. Substitute the values into the point-slope form, \(y−y_1=m(x−x_1)\).
4. Write the equation in slope-intercept form or in the form \(x=a\).

Example \(\PageIndex{10}\)

Find an equation of a horizontal line that contains the point \((−2,−6)\). Write the equation in slope-intercept form.

Solution

Every horizontal line has slope \(0\). We can substitute the slope and a point into the point-slope form, \(y−y_1=m(x−x_1)\). We need the slope and the point.

Identify the slope.	\(m=0\)
Identify the point.	\(\underbrace{(-2,-6)}_{(x_1,y_1)}\)
Substitute the values into \(y−y_1=m(x−x_1)\).	\(\begin{aligned} y−y_1&=m(x−x_1) \\ y−(-6)&=0(x−(-2))\end{aligned}\)
Simplify.	\(y+6=0\)
Solve for \(y\).	\(y=-6\)
Write in slope-intercept form.	It is in \(y\)-form, but it could be written as \(y=0x−6\).
Answer the question.	The equation of the horizontal line is \(y=-6\) or \(y=0x-6\).

Did we end up with the form of a horizontal line, \(y=a\)?

Try It \(\PageIndex{11}\)

Find an equation of a horizontal line that contains the point \((−3,8)\). Write the equation in slope-intercept form.

Answer

The equation is \(y=8\).

Try It \(\PageIndex{12}\)

Find an equation of a horizontal line that contains the point \((−1,4)\). Write the equation in slope-intercept form.

Answer

The equation is \(y=4\).

Find an Equation of the Line Given Two Points

When real-world data is collected, a linear model can be created from two data points. In the next example we will see how to find an equation of a line when just two points are given.

So far, we have two options for finding an equation of a line: by using the slope-intercept form or by using the point-slope form. When we start with two points, it makes more sense to use the point-slope form. But then we need the slope. Can we find the slope with just two points? Yes. Then, once we have the slope, we can use it and one of the given points to find an equation. While our equation is an equation for the given line, we will then rewrite our equation in slope-intercept form, or in the form \(x=a\) so that our answer is unique.

Example \(\PageIndex{13}\)

Find an equation of the line that contains the points \((−3,−1)\) and \((2,−2)\). Write the equation in slope-intercept form.

Solution

In order to find the equation of the line using the point-slope form, we need the slope and the point.

Write the given points.	\((−3,−1)\) and \((2,−2)\)
Choose one point and identify \(x_1\) and \(y_1\).	\(\underbrace{(−3,-1)}_{(x_1,y_1)}\) \(x_1=-3\) \(y_1=-1\)
Pick the other point and identify \(x_2\) and \(y_2\).	\(\underbrace{(2,-2)}_{(x_2,y_2)}\) \(x_2=2\) \(y_2=-2\)
Find the slope, using \(m=\dfrac{y_2−y_1}{x_2−x_1}\).	\(\begin{aligned}m&=\dfrac{y_2−y_1}{x_2−x_1} \\m &=\dfrac{-2-(-1)}{2-(-3)} \\ m& =\dfrac{−1}{5} \\ m& =-\dfrac{1}{5} \end{aligned}\) The slope is \(m=-\dfrac{1}{5}\).
Substitute the values into the point-slope form, \(y-y_1=m(x-x_1)\).	\(\begin{aligned} y-y_1&=m(x-x_1)\\ y-(-1) &=-\dfrac{1}{5}(x-(-3)) \end{aligned}\)
Simplify to write the equation in slope-intercept form, \(y=mx+b\).	\(\begin{aligned} y+1 &= -\dfrac{1}{5}(x+3) \\ y+1 &= -\dfrac{1}{5}x-\dfrac{3}{5} \\y &= -\dfrac{1}{5}x-\dfrac{8}{5}\end{aligned}\)
Answer the question.	The equation of the line is \(y = -\dfrac{1}{5}x-\dfrac{8}{5}\).

Try It \(\PageIndex{14}\)

Find the equation of a line that contains the points \((−2,−4)\) and \((1,−3)\). Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=\dfrac{1}{3}x−\dfrac{10}{3}\).

Try It \(\PageIndex{15}\)

Find the equation of a line that contains the points \((−4,−3)\) and \((1,−5)\). Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=−\dfrac{2}{5}x−\dfrac{23}{5}\).

The steps are summarized here.

To find an equation of a line given two points

1. Find the slope using the given points: \(m=\dfrac{y_2−y_1}{x_2−x_1}\).
2. Choose one point.
3. Substitute the values into the point-slope form: \(y−y_1=m(x−x_1)\).
4. Write the equation in slope-intercept form.

Example \(\PageIndex{16}\)

Find an equation of a line that contains the points \((−3,5)\) and \((−3,4)\). Write the equation in slope-intercept form.

Solution

In order to find the equation of the line using the point-slope form, we need the slope and the point.

Write the given points.	\((−3,5)\) and \((−3,4)\)
Choose one point, name it \((x_1,y_1)\), and identify \(x_1\) and \(y_1\).	\(\underbrace{(−3,5)}_{(x_1,y_1)}\) \(x_1=-3\) \(y_1=5\)
Pick the other point, name it \((x_2,y_2)\), and identify \(x_2\) and \(y_2\).	\(\underbrace{(−3,4)}_{(x_2,y_2)}\) \(x_2=-3\) \(y_2=4\)
Find the slope, using \(m=\dfrac{y_2−y_1}{x_2−x_1}\).	\(\begin{aligned}m&=\dfrac{y_2−y_1}{x_2−x_1} \\m &=\dfrac{4−5}{−3−(−3)} \\ m& =\dfrac{−1}{0} \end{aligned}\) The slope is undefined.
Conclusion.	This tells us it is a vertical line. Both of our points have an \(x\)-coordinate of \(−2\). So our equation of the line is \(x=−2\). Since there is no \(y\), we cannot write it in slope-intercept form.

We may want to sketch a graph using the two given points. Does the graph agree with our conclusion that this is a vertical line?

Try It \(\PageIndex{17}\)

Find the equation of a line that contains the points \((5,1)\) and \((5,−4)\).

Answer

The equation of the line is \(x=5\).

Try It \(\PageIndex{18}\)

Find the equation of a line that contains the points \((−4,4)\) and \((−4,3)\).

Answer

The equation of the line is \(x=−4\).

We have seen that we can use the slope-intercept form or the point-slope form to find an equation of a line. Which form we use will depend on the information we are given.

To write an equation of a line
If given:	Use:	Form:
Slope and \(y\)-intercept	slope-intercept	\(y=mx+b\)
Slope and a point	point-slope	\(y−y_1=m(x−x_1)\)
Two points	point-slope	\(y−y_1=m(x−x_1)\)

Find an Equation of a Line Parallel to a Given Line

Suppose we need to find an equation of a line that passes through a specific point and is parallel to a given line. We can use the fact that parallel lines have the same slope. So we will have a point and the slope - just what we need to use the point-slope equation.

First, let’s look at this graphically.

This graph shows \(y=2x−3.\) We want to graph a line parallel to this line and passing through the point \((−2,1)\).

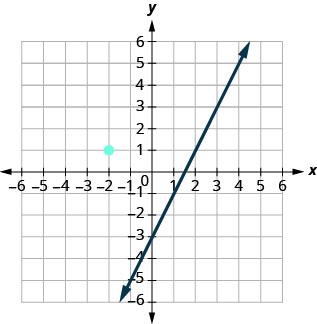
We know that parallel lines have the same slope. So the second line will have the same slope as \(y=2x−3\). That slope is \(m_{||}=2\). We’ll use the notation \(m_{||}\) to represent the slope of a line parallel to a line with slope \(m\). (Notice that the subscript \(||\) looks like two parallel lines.)

The second line will pass through \((−2,1)\) and have \(m=2\).

To graph the line, we start at \((−2,1)\) and count out the rise and run.

With \(m=2\) (or \(m=\dfrac{2}{1}\)), we count out the rise 2 and the run 1. We draw the line, as shown in the graph.

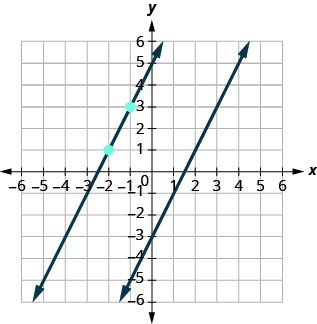
Do the lines appear parallel? Does the second line pass through \((−2,1)\)?

We were asked to graph the line, now let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. Here we know one point and can find the slope. So we will use the point-slope form.

Example \(\PageIndex{19}\)

Find an equation of a line parallel to \(y=2x−3\) that contains the point \((−2,1)\). Write the equation in slope-intercept form.

Solution

\(y=2x−3\)
Find the slope of the given line.	The line is in slope-intercept form, \(y=2x-3\).	\(m=2\)
Find the slope of the parallel line.	Parallel lines have the same slopes.	\(m_\parallel=2\)
Identify the point.	The given point is \((-2,1)\).	\(\underbrace{(-2,1)}_{(x_1,y_1)}\)
Substitute the values into the point-slope form, \(y-y_1=m(x-x_1)\).	Simplify.	\(\begin{aligned}y-y_1&=m(x-x_1)\\ y-1 &=2(x-(-2))\\ y-1 &=2(x+2) \\y-1&=2x+4\end{aligned}\)
Write the equation in slope-intercept form.		\(y=2x+5\)

Look at graph with the parallel lines shown previously. Does this equation make sense? What is the \(y\)-intercept of the line? What is the slope?

Try It \(\PageIndex{20}\)

Find an equation of a line parallel to the line \(y=3x+1\) that contains the point \((4,2)\). Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=3x−10\).

Try It \(\PageIndex{21}\)

Find an equation of a line parallel to the line \(y=\dfrac{1}{2}x−3\) that contains the point \((6,4)\). Write the equation in slope-intercept form.

Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=\dfrac{1}{2}x+1\).

Find an equation of a line parallel to a given line

1. Find the slope of the given line.
2. Find the slope of the parallel line.
3. Identify the point.
4. Substitute the values into the point-slope form: \(y−y_1=m(x−x_1)\).
5. Write the equation in slope-intercept form.

Find an Equation of a Line Perpendicular to a Given Line

Now, let’s consider perpendicular lines. Suppose we need to find the line passing through a specific point and which is perpendicular to a given line. We can use the fact that perpendicular lines have slopes that are negative reciprocals. We will again use the point-slope equation, like we did with parallel lines.

This graph shows \(y=2x−3\). Now, we want to graph a line perpendicular to this line and passing through \((−2,1)\).

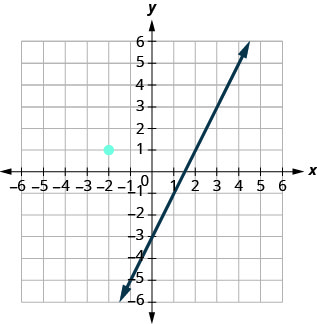
We know that perpendicular lines have slopes that are negative reciprocals.

We will use the notation \(m_⊥\) to represent the slope of a line perpendicular to a line with slope \(m\). (Notice that the subscript \(⊥\) looks like the right angles made by two perpendicular lines.)

\[y=2x−3 \quad \text{ perpendicular line} \nonumber\]

\[m=2 \qquad m_⊥=−\dfrac{1}{2}\nonumber\]

We now know the perpendicular line will pass through \((−2,1)\) with \(m_⊥=−\dfrac{1}{2}\).

To graph the line, we will start at \((−2,1)\) and count out the rise \(−1\) and the run \(2\). Then we draw the line.

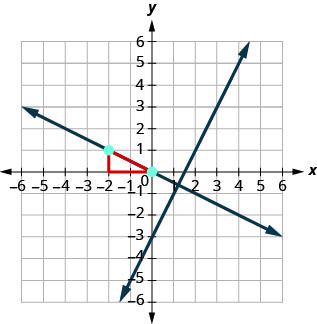
Do the lines appear perpendicular? Does the second line pass through \((−2,1)\)?

We were asked to graph the line, now, let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. In this Example we know one point, and can find the slope, so we will use the point-slope form.

Example \(\PageIndex{22}\)

Find an equation of a line perpendicular to \(y=2x−3\) that contains the point \((−2,1)\). Write the equation in slope-intercept form.

Solution

\(y=2x-3\)
Find the slope of the given line.	The line is in slope-intercept form, \(y=2x-3\).	\(m=2\)
Find the slope of the perpendicular line.	The slopes of perpendicular lines are negative.	\(m_{\perp}=-\dfrac{1}{2}\)
Identify the point.	The given point is \((-2,1)\).	\(\underbrace{(-2,1)}_{(x_1,y_1)}\)
Substitute the values into the point-slope form, \(y-y_1=m(x-x_1)\).	Simplify.	\(\begin{aligned}y-y_1&=m(x-x_1)\\ y-1 &=-\dfrac{1}{2}(x-(-2))\\ y-1 &=-\dfrac{1}{2}(x+2) \\y-1&=-\dfrac{1}{2}x-1\end{aligned}\)
Write the equation in slope-intercept form.		\(y=-\dfrac{1}{2}x\)
Answer the question.	The equation of the line is \(y=-\dfrac{1}{2}x\).

Try It \(\PageIndex{23}\)

Find an equation of a line perpendicular to the line \(y=3x+1\) that contains the point \((4,2)\). Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=−\dfrac{1}{3}x+\dfrac{10}{3}\).

Try It \(\PageIndex{24}\)

Find an equation of a line perpendicular to the line \(y=\dfrac{1}{2}x−3\) that contains the point \((6,4)\). Write the equation in slope-intercept form.

Answer

The equation of the line is \(y=−2x+16\).

Find an equation of a line perpendicular to a given line

1. Find the slope of the given line.
2. Find the slope of the perpendicular line.
3. Identify the point.
4. Substitute the values into the point-slope form, \(y−y_1=m(x−x_1)\).
5. Write the equation in slope-intercept form.

Example \(\PageIndex{25}\)

Find an equation of a line perpendicular to \(x=5\) that contains the point \((3,−2)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Solution

Again, since we know one point, the point-slope option seems more promising than the slope-intercept option. We need the slope to use this form, and we know the new line will be perpendicular to \(x=5\). This line is vertical, so its perpendicular will be horizontal. This tells us the \(m_⊥=0\).

Identify the point.	\((3,−2)\)
Identify the slope of the perpendicular line.	\(m_{\perp}=0\)
Substitute the values into \(y−y_1=m(x−x_1)\).	\(y-(-2)=0(x-3)\)
Simplify.	\(y+2=0\)
Write the equation in slope-intercept form.	\(y=-2\)
Answer the question.	The equation of the line is \(y=-2\).

Sketch the graph of both lines. On the graph, do the lines appear to be perpendicular?

Try It \(\PageIndex{26}\)

Find an equation of a line that is perpendicular to the line \(x=4\) that contains the point \((4,−5)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Answer

The equation of the line is \(y=−5\).

Try It \(\PageIndex{27}\)

Find an equation of a line that is perpendicular to the line \(x=2\) that contains the point \((2,−1)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Answer

The equation of the line is \(y=−1\).

In Example 1.3.25, we used the point-slope form to find the equation. We could have looked at this in a different way.

We want to find a line that is perpendicular to \(x=5\) that contains the point \((3,−2)\). This graph shows us the line \(x=5\) and the point \((3,−2)\).

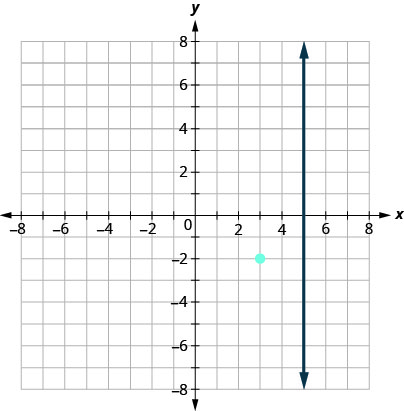
We know every line perpendicular to a vertical line is horizontal, so we will sketch the horizontal line through \((3,−2)\).

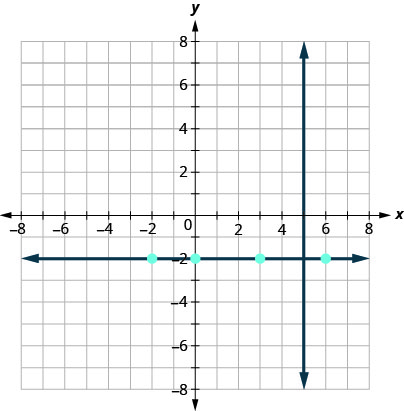
Do the lines appear perpendicular?

If we look at a few points on this horizontal line, we notice they all have \(y\)-coordinates of \(−2\). So, the equation of the line perpendicular to the vertical line \(x=5\) is \(y=−2\).

Example \(\PageIndex{28}\)

Find an equation of a line that is perpendicular to \(y=−3\) that contains the point \((−3,5)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Solution

The line \(y=−3\) is a horizontal line. Any line perpendicular to it must be vertical, in the form \(x=a\). Since the perpendicular line is vertical and passes through \((−3,5)\), every point on it has an \(x\)-coordinate of \(−3\). The equation of the perpendicular line is \(x=−3\).

We may want to sketch the lines. Do they appear perpendicular?

Try It \(\PageIndex{29}\)

Find an equation of a line that is perpendicular to the line \(y=1\) that contains the point \((−5,1)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Answer

The equation of the line is \(x=−5\).

Try It \(\PageIndex{30}\)

Find an equation of a line that is perpendicular to the line \(y=−5\) that contains the point \((−4,−5)\). Write the equation in slope-intercept form, or in the form \(x=a\).

Answer

The equation of the line is \(x=−4\).

Key Concepts

• How to find an equation of a line given the slope and a point.
  1. Identify the slope.
  2. Identify the point.
  3. Substitute the values into the point-slope form,\( y−y_1=m(x−x_1)\).
  4. Write the equation in slope-intercept form.
• How to find an equation of a line given two points.
  1. Find the slope using the given points. \(m=\dfrac{y_2−y_1}{x_2−x_1}\)
  2. Choose one point.
  3. Substitute the values into the point-slope form: \(y−y_1=m(x−x_1)\).
  4. Write the equation in slope-intercept form.

     To Write an Equation of a Line
     If given:	Use:	Form:
     Slope and \(y\)-intercept	slope-intercept	\(y=mx+b\)
     Slope and a point	point-slope	\(y−y_1=m(x−x_1)\)
     Two points	point-slope	\(y−y_1=m(x−x_1)\)

• How to find an equation of a line parallel to a given line.
  1. Find the slope of the given line.
  2. Find the slope of the parallel line.
  3. Identify the point.
  4. Substitute the values into the point-slope form: \(y−y_1=m(x−x_1)\).
  5. Write the equation in slope-intercept form
• How to find an equation of a line perpendicular to a given line.
  1. Find the slope of the given line.
  2. Find the slope of the perpendicular line.
  3. Identify the point.
  4. Substitute the values into the point-slope form, \(y−y_1=m(x−x_1)\).
  5. Write the equation in slope-intercept form.

Glossary

point-slope form

The point-slope form of an equation of a line with slope m and containing the point \((x_1,y_1)\) is \(y−y_1=m(x−x_1)\).

Practice Makes Perfect

In the below, when we write "Write the equation in slope-intercept form" we mean "Write the equation in slope-intercept form or in the form \(x=a\)."

Find an Equation of the Line Given the Slope and y-Intercept

In the following exercises, find the equation of a line with given slope and y-intercept. Write the equation in slope-intercept form.

1. slope \(3\) and \(y\)-intercept \((0,5)\)

Answer

\(y=3x+5\)

2. slope \(8\) and \(y\)-intercept \((0,−6)\)

3. slope \(−3\) and \(y\)-intercept \((0,−1)\)

Answer

\(y=−3x−1\)

4. slope \(−1\) and \(y\)-intercept \((0,3)\)

5. slope \(\dfrac{1}{5}\) and \(y\)-intercept \((0,−5)\)

Answer

\(y=\dfrac{1}{5}x−5\)

6. slope \(−\dfrac{3}{4}\) and \(y\)-intercept \((0,−2)\)

7. slope \(0\) and \(y\)-intercept \((0,−1)\)

Answer

\(y=−1\)

8. slope \(−4\) and \(y\)-intercept \((0,0)\)

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope-intercept form.

9.

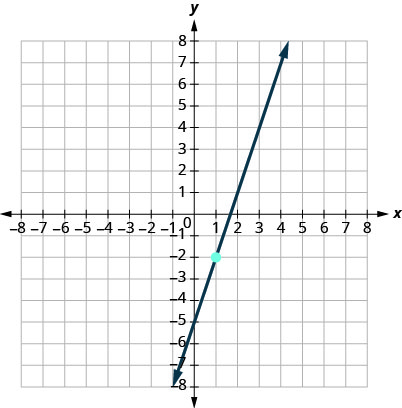
Answer

\(y=3x−5\)

10.

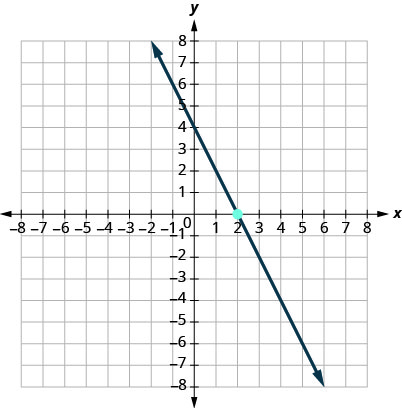
11.

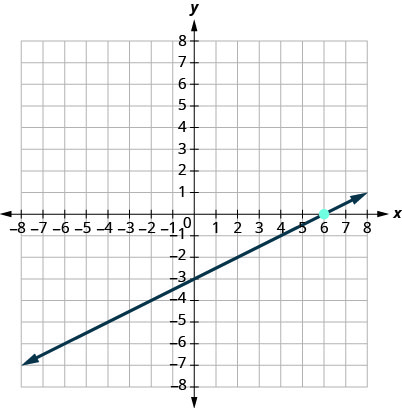
Answer

\(y=\dfrac{1}{2}x−3\)

12.

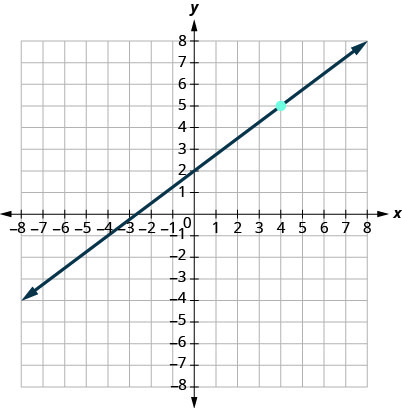
13.

Answer

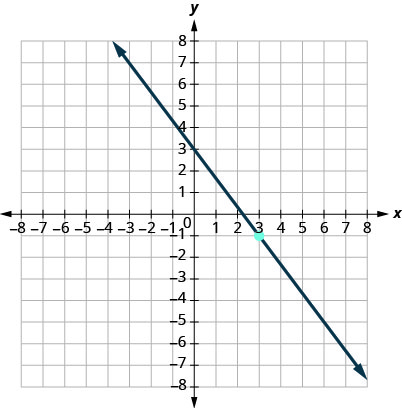
\(y=−\dfrac{4}{3}x+3\)

14.

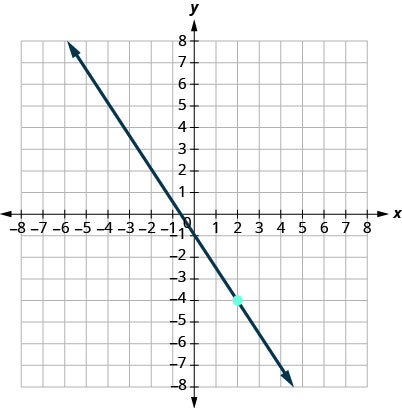
15.

Answer

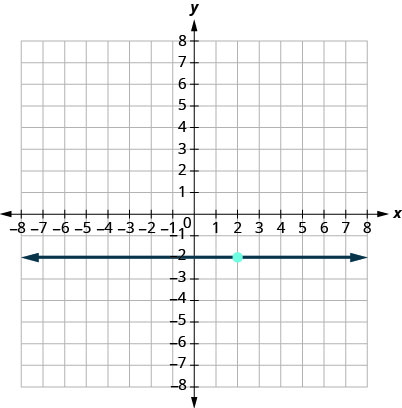
\(y=−2\)

16.

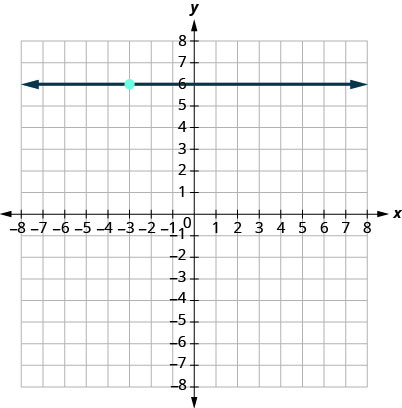
Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope-intercept form.

17. \(m=\dfrac{5}{8}\), point \((8,3)\)

Answer

\(y=\dfrac{5}{8}x−2\)

18. \(m=\dfrac{5}{6}\), point \((6,7)\)

19. \(m=−\dfrac{3}{5}\), point \((10,−5)\)

Answer

\(y=−\dfrac{3}{5}x+1\)

20. \(m=−\dfrac{3}{4}\), point \((8,−5)\)

21. \(m=−\dfrac{3}{2}\), point \((−4,−3)\)

Answer

\(y=−\dfrac{3}{2}x+9\)

22. \(m=−\dfrac{5}{2}\), point \((−8,−2)\)

23. \(m=−7\), point \((−1,−3)\)

Answer

\(y=−7x−10\)

24. \(m=−4\), point \((−2,−3)\)

25. Horizontal line containing \((−2,5)\)

Answer

\(y=5\)

26. Horizontal line containing \((−2,−3)\)

27. Horizontal line containing \((−1,−7)\)

Answer

\(y=−7\)

28. Horizontal line containing \((4,−8)\)

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope-intercept form.

29. \((2,6)\) and \((5,3)\)

Answer

\(y=−x+8\)

30. \((4,3)\) and \((8,1)\)

31. \((−3,−4)\) and \((5−2)\).

Answer

\(y=\dfrac{1}{4}x−\dfrac{13}{4}\)

32. \((−5,−3)\) and \((4,−6)\).

33. \((−1,3)\) and \((−6,−7)\).

Answer

\(y=2x+5\)

34. \((−2,8)\) and \((−4,−6)\).

35. \((0,4)\) and \((2,−3)\).

Answer

\(y=−\dfrac{7}{2}x+4\)

36. \((0,−2)\) and \((−5,−3)\).

37. \((7,2)\) and \((7,−2)\).

Answer

\(x=7\)

38. \((−2,1)\) and \((−2,−4)\).

39. \((3,−4)\) and \((5,−4)\).

Answer

\(y=−4\)

40. \((−6,−3)\) and \((−1,−3)\)

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope-intercept form.

41. line \(y=4x+2\), point \((1,2)\)

Answer

\(y=4x−2\)

42. line \(y=−3x−1\), point \(2,−3)\).

43. line \(2x−y=6\), point \((3,0)\).

Answer

\(y=2x−6\)

44. line \(2x+3y=6\), point \((0,5)\).

45. line \(x=−4\), point \((−3,−5)\).

Answer

\(x=−3\)

46. line \(x−2=0\), point \((1,−2)\)

47. line \(y=5\), point \((2,−2)\)

Answer

\(y=−2\)

48. line \(y+2=0\), point \((3,−3)\)

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope-intercept form.

49. line \(y=−2x+3\), point \((2,2)\)

Answer

\(y=\dfrac{1}{2}x+1\)

50. line \(y=−x+5\), point \((3,3)\)

51. line \(y=\dfrac{3}{4}x−2\), point \((−3,4)\)

Answer

\(y=−\dfrac{4}{3}x\)

52. line \(y=\dfrac{2}{3}x−4\), point \((2,−4)\)

53. line \(2x−3y=8\), point \((4,−1)\)

Answer

\(y=−\dfrac{3}{2}x+5\)

54. line \(4x−3y=5\), point \((−3,2)\)

55. line \(2x+5y=6\), point \((0,0)\)

Answer

\(y=\dfrac{5}{2}x\)

56. line \(4x+5y=−3\), point \((0,0)\)

57. line \(x=3\), point \((3,4)\)

Answer

\(y=4\)

58. line \(x=−5\), point \((1,−2)\)

59. line \(x=7\), point \((−3,−4)\)

Answer

\(y=−4\)

60. line \(x=−1\), point \((−4,0)\)

61. line \(y−3=0\), point \((−2,−4)\)

Answer

\(x=−2\)

62. line \(y−6=0\), point \((−5,−3)\)

63. line \(y\)-axis, point \((3,4)\)

Answer

\(y=4\)

64. line \(y\)-axis, point \((2,1)\)

Mixed Practice

In the following exercises, find the equation of each line. Write the equation in slope-intercept form.

65. Containing the points \((4,3)\) and \((8,1)\)

Answer

\(y=−\dfrac{1}{2}x+5\)

66. Containing the points \((−2,0)\) and \((−3,−2)\)

67. \(m=\dfrac{1}{6}\), containing point \((6,1)\)

Answer

\(y=\dfrac{1}{6}x\)

68. \(m=\dfrac{5}{6}\), containing point \((6,7)\)

69. Parallel to the line \(4x+3y=6\), containing point \((0,−3)\)

Answer

\(y=−\dfrac{4}{3}x−3\)

70. Parallel to the line \(2x+3y=6\), containing point \((0,5)\)

71. \(m=−\dfrac{3}{4}\), containing point \((8,−5)\)

Answer

\(y=−\dfrac{3}{4}x+1\)

72. \(m=−\dfrac{3}{5}\), containing point \((10,−5)\)

73. Perpendicular to the line \(y−1=0\), point \((−2,6)\)

Answer

\(x=−2\)

74. Perpendicular to the line y-axis, point \((−6,2)\)

75. Parallel to the line \(x=−3\), containing point \((−2,−1)\)

Answer

\(x=−2\)

76. Parallel to the line \(x=−4\), containing point \((−3,−5)\)

77. Containing the points \((−3,−4)\) and \((2,−5)\)

Answer

\(y=−\dfrac{1}{5}x−\dfrac{23}{5}\)

78. Containing the points \((−5,−3)\) and \((4,−6)\)

79. Perpendicular to the line \(x−2y=5\), point \((−2,2)\)

Answer

\(y=−2x−2\)

80. Perpendicular to the line \(4x+3y=1\), point \((0,0)\)

Writing Exercises

81. Why are all horizontal lines parallel?

Answer

Answers will vary.

82. Explain in your own words why the slopes of two perpendicular lines must have opposite signs.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?