2.1: Solve Systems of Linear Equations with Two Variables
- Page ID
- 66287
By the end of this section, you will be able to:
- Determine whether an ordered pair is a solution of a system of equations
- Solve a system of linear equations by graphing
- Solve a system of equations by substitution
- Solve a system of equations by elimination
- Choose the most convenient method to solve a system of linear equations
Before you get started, take this readiness quiz.
1. For the equation \(y=\dfrac{2}{3}x−4\),
a. Is \((6,0)\) a solution?
b. Is \((−3,−2)\) a solution?
2. Find the slope and \(y\)-intercept of the line \(3x−y=12\).
3. Find the \(x\)- and \(y\)-intercepts of the line \(2x−3y=12\).
If you missed any of these problems, review [link].
Determine Whether an Ordered Pair is a Solution of a System of Equations
We have learned about solutions to linear equations with two variables. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations.
When two or more linear equations are grouped together, they form a system of linear equations.
In this section, we will focus our work on systems of two linear equations with two unknowns. We will solve larger systems of equations later in this chapter.
An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.
\[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]
A linear equation in two variables, such as \(2x+y=7\), has an infinite number of solutions. Its graph is a line. Remember, every point on the line is a solution to the equation and every solution to the equation is a point on the line.
To solve a system of two linear equations, we want to find the values of the variables that are solutions to both equations. In other words, we are looking for the ordered pairs \((p,q)\) that when substituted in for \((x,y)\) (\(p\) for \(x\) and \(q\) for \(y\)) make both equations true. These are called the solutions of a system of equations.
The solutions of a system of equations are the values of the variables that make all the equations true. A solution of a system of two linear equations is represented by an ordered pair \((p,q)\). We say \((x,y)\)=\((p,q)\) is a solution to the system if when when we substitute \(p\) for \(x\) and \(q\) for \(y\), both resulting equations are true.
To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.
Determine whether the ordered pair is a solution to the system \(\left \{ \begin{array}{l} x−y = −1 \\ 2x−y = −5 \end{array}\right. .\)
a. \((−2,−1)\)
b. \((−4,−3)\)
- Solution
-
a.
\(x-y=-1\) \(2x-y=-5\) We substitute \(-2\) for \(x\) and \(-1\) for \(y\) in both equations. \(\begin{aligned} x-y&=-1 \\ -2-(-1) & \stackrel{?}{=} -1 \\-1 & \stackrel{?}{=} -1 \quad \text{True}\end{aligned}\) \(\begin{aligned} 2x-y&=-5 \\ 2(-2)-(-1) & \stackrel{?}{=} -5 \\-3 & \stackrel{?}{=} -5 \quad \text{False}\end{aligned}\) Is \((-2,1)\) a solution to the equation? Yes No Answer the question. Since substituting in \((-2,-1)\) does not make both equations true, \((-2,-1)\) is not a solution. b.
\(x-y=-1\) \(2x-y=-5\) We substitute \(-4\) for \(x\) and \(-3\) for \(y\) in both equations. \(\begin{aligned} x-y&=-1 \\ -4-(-3) & \stackrel{?}{=} -1 \\-1 & \stackrel{?}{=} -1 \quad \text{True}\end{aligned}\) \(\begin{aligned} 2x-y&=-5 \\ 2(-4)-(-3) & \stackrel{?}{=} -5 \\-5 & \stackrel{?}{=} -5 \quad \text{True}\end{aligned}\) Is \((-4,-3)\) a solution to the equation? Yes Yes Answer the question. Since substituting in \((-4,-3)\) does make both equations true, \((-4,-3)\) is not a solution.
Determine whether the ordered pair is a solution to the system \(\left \{ \begin{aligned} 3x+y &= 0 \\ x+2y &= −5 \end{aligned} \right. \).
a. \((1,−3)\)
b. \((0,0)\)
- Answer
-
a. It is a solution.
b. It is not a solution.
Determine whether the ordered pair is a solution to the system \(\left \{ \begin{array}{l} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \).
a. \((2,−2)\)
b. \((−2,2)\)
- Answer
-
a. It is not a solution.
b. It is a solution.
Solve a System of Linear Equations by Graphing
In this section, we will use three methods to solve a system of linear equations. The first method we will use is graphing.
The graph of a linear equation is a line. With the representation of ordered pairs of numbers on the coordinate plane, we will call these ordered pairs points and imagine them on the coordinate plane. So, we will say, for example, that each point on the line is a solution to the equation instead of that each point on the line represents a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we will find the solution to the system.
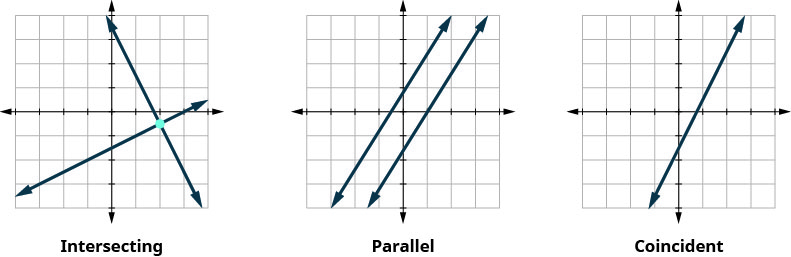
When we solve a system of two linear equations represented by a graph of two lines in the same plane. There are three possible cases, as shown.

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section we will decide which method was the most convenient way to solve this system.
Solve the system \( \left\{ \begin{aligned} 2x+y &= 7 \\ x−2y &= 6 \end{aligned} \right.\) by graphing.
- Solution
-
\( \left\{ \begin{aligned} 2x+y &= 7 \\ x−2y &= 6 \end{aligned} \right.\) Graph the first equation. To graph the first line, write the equation in slope-intercept form.
\(\begin{aligned} 2x+y&=7\\ y&= -2x+7 \end{aligned}\)
The slope is \(m=-2\).
The \(y\)-intercept is \((0,7)\), so \(b=7\).
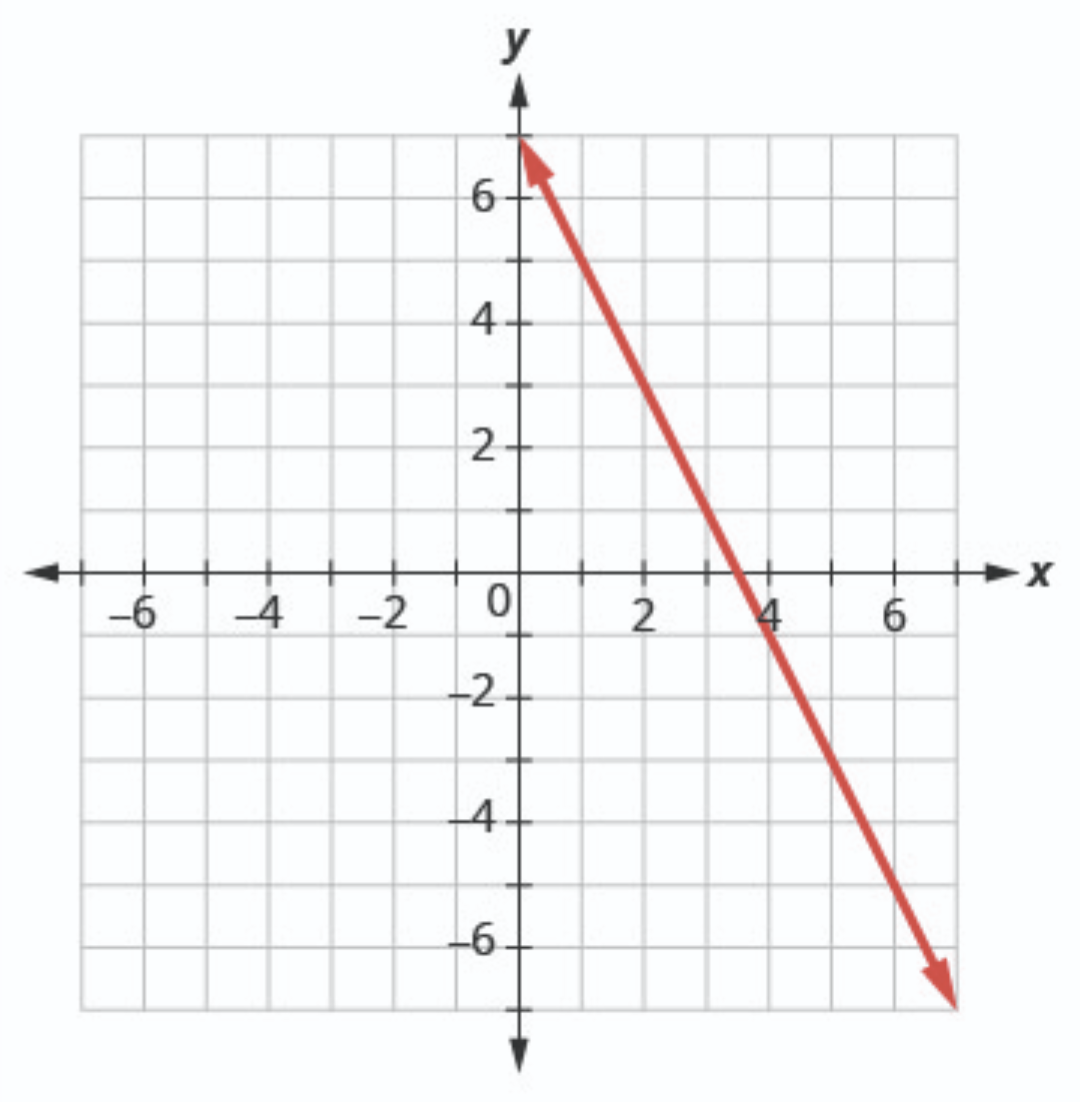
Graph the second equation on the same rectangular coordinate system. To graph the second line,
\(x-2y=6\)
use intercepts.
The \(x\)-intercept is \((6,0)\).
The \(y\)-intercept is \((0,-3)\).
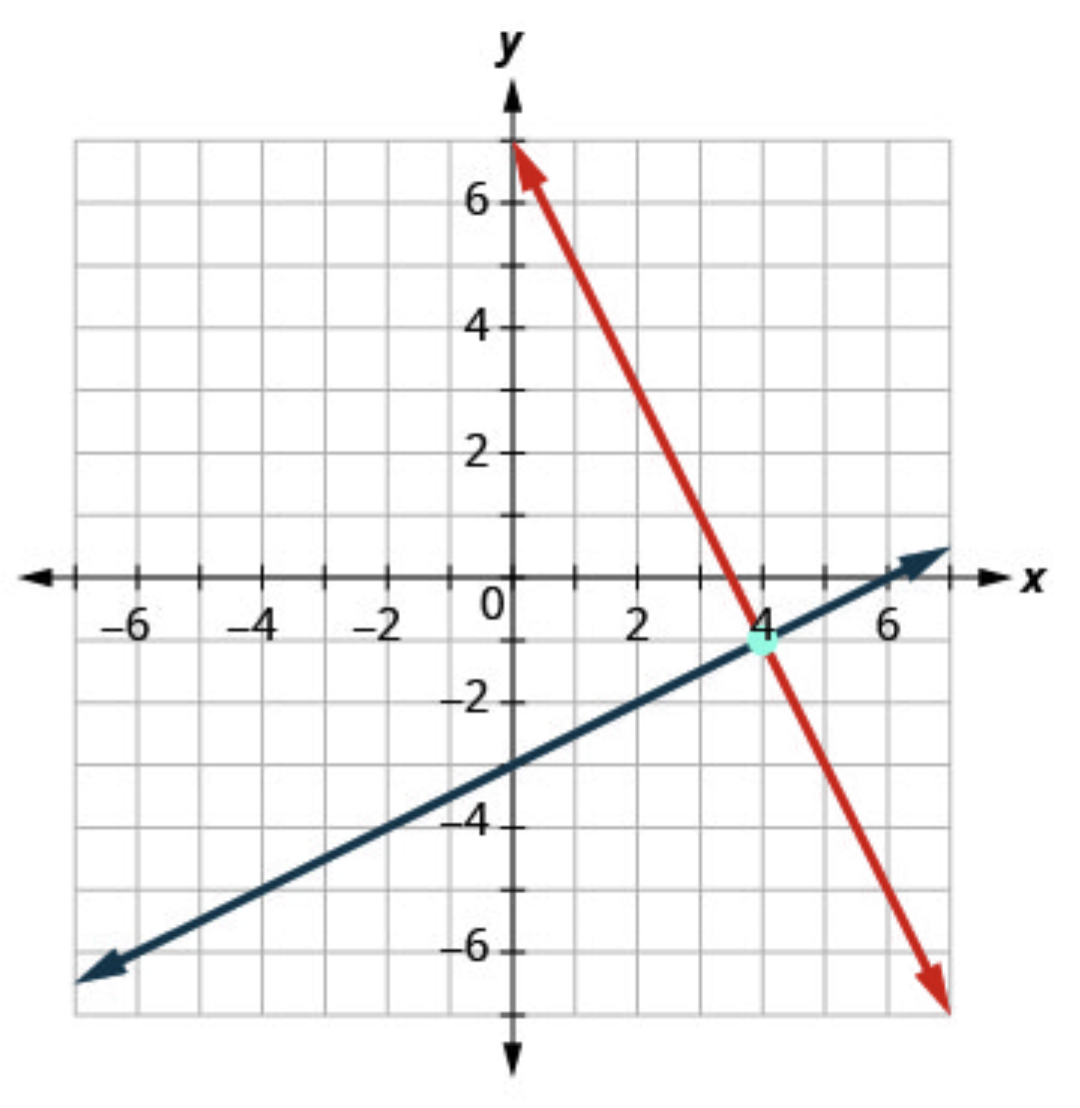
Determine whether the lines intersect, are parallel, or are the same line. Look at the graph of the lines. The lines intersect. Identify the solution to the system.
- If the lines intersect, identify the point of intersection. Check to make sure it is a solution to both equations. This is the solution to the system.
- If the lines are parallel, the system has no solution.
- If the lines are the same, the system has an infinite number of solutions.
Since the lines intersect, find the point of intersection.
Check the point in both equations.
The lines intersect at \((4,-1)\).
\(\begin{aligned} 2x+y&=7 \\ 2(4)+(-1) & \stackrel{?}{=} 7 \\7 & \stackrel{?}{=} 7\\ &\quad \text{True}\end{aligned}\quad\quad\begin{aligned} x-2y&=6 \\ 4-2(-1)& \stackrel{?}{=} 6 \\6 & \stackrel{?}{=} 6 \\ &\quad \text{True}\end{aligned}\)
Substituting \((4,-1)\) in for \((x,y)\) makes both equations true.
Answer the question. The solution is \((4,-1)\).
Solve the system \( \left\{ \begin{array}{l} x−3y = −3 \\ x+y = 5 \end{array} \right.\) by graphing.
- Answer
-
The solution is \((3,2)\).
Solve the system \( \left\{ \begin{array}{l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\) by graphing.
- Answer
-
The solution is \((2,3)\).
The steps to use to solve a system of linear equations by graphing are shown here.
- Graph the first equation.
- Graph the second equation on the same rectangular coordinate system.
- Determine whether the lines intersect, are parallel, or are the same line.
- Identify the solution to the system.
- If the lines intersect, identify the point of intersection. This is the solution to the system.
- If the lines are parallel, the system has no solution.
- If the lines are the same, the system has an infinite number of solutions.
- Check the solution in both equations.
In the next example, we will first rewrite the equations into slope-intercept form as this will make it easy for us to quickly graph the lines.
Solve the system \(\left\{ \begin{aligned} 3x+y &= −1 \\ 2x+y& = 0 \end{aligned}\right.\) by graphing.
- Solution
-
We will solve both of these equations for \(y\) so that we can easily graph them using their slopes and \(y\)-intercepts.
\(\left\{ \begin{aligned} 3x+y &= −1 \\ 2x+y &= 0 \end{aligned}\right.\) Solve the first equation for \(y\). \(\begin{aligned} 3x+y &= -1 \\ y &= -3x-1\end{aligned}\) Find the slope and \(y\)-intercept. The slope is \(m=-3\).
The \(y\)-intercept is \((0,-1)\).
Solve the second equation for \(y\). \(\begin{aligned} 2x+y &= 0 \\ y &= -2x\end{aligned}\)
Find the slope and \(y\)-intercept. The slope is \(m=-2\).
The \(y\)-intercept is \((0,0)\).
Graph the lines. 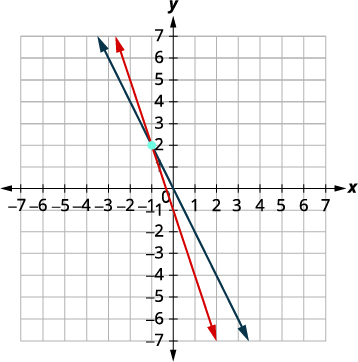
Determine the point of intersection. The lines intersect at \((−1,2)\). Check the solution in both equations.
\(\begin{aligned} 3x+y&=-1 \\ 3(-1)+2 & \stackrel{?}{=} -1 \\-1 & \stackrel{?}{=} -1\\ &\quad \text{True}\end{aligned}\quad\quad\begin{aligned} 2x+y&=0 \\ 2(-1)+2 & \stackrel{?}{=} 0 \\0 & \stackrel{?}{=} 0 \\ &\quad \text{True}\end{aligned}\)
Substituting \((-1,2)\) in for \((x,y)\) makes both equations true.
Answer the question. The solution is \((−1,2)\).
Solve the system \(\left\{ \begin{array}{l} −x+y = 1 \\2x+y = 10 \end{array}\right.\) by graphing.
- Answer
-
The solution is \((3,4)\).
Solve the system \(\left\{\begin{array}{l} 2x+y = 6 \\x+y = 1 \end{array}\right.\) by graphing.
- Answer
-
The solution is \((5,−4)\).
In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.
Solve the system \(\left\{ \begin{array}{l} y = \dfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right.\) by graphing.
- Solution
-
\(\left\{ \begin{array} {l} y = \dfrac{1}{2}x-3 \\ x-2y= 4 \end{array}\right. \) To graph the first equation, we will use its
slope and \(y\)-intercept.\(y = \dfrac{1}{2}x-3\)
The slope is \(m=\dfrac{1}{2}\).
The \(y\)-intercept is \((0,-3)\).
To graph the second equation, we will use
the intercepts.\(x-2y=4\) Find the \(x\)- and \(y\)-intercepts of the second equation. \(x\) \(y\) \((x,y)\) \(0\) \(-2\) \((0,-2)\) \(4\) \(0\) \((4,0)\) The \(x\)-intercept is \((4,0)\).
The \(y\)-intercept is \((0,-2)\).
Graph the lines. 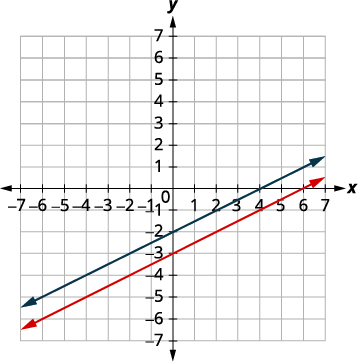
Determine the points of intersection. The lines are parallel.
Since no point is on both lines, there is no
ordered pair that makes both equations
true upon substitution.Answer the question. There is no solution to the system.
Solve the system \(\left\{\begin{array}{l} y = -\dfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right.\) by graphing.
- Answer
-
The system has no solution.
Solve the system \(\left\{ \begin{array}{l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right.\) by graphing.
- Answer
-
The system has no solution.
Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that, when substituted, make both equations true. Therefore there are infinitely many solutions to the system.
Solve the system \(\left\{ \begin{array}{l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right.\) by graphing.
- Solution
-
\(\left\{\begin{array}{l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \) Find the slope and \(y\)-intercept of the first equation. \(y = 2x-3\)
The slope is \(m=2\).
The \(y\)-intercept is \((0,-3)\).
To graph the second equation, we will use
the intercepts.\(-6x+3y = 9\) Find the \(x\)- and \(y\)-intercepts of the second equation. \(x\) \(y\) \((x,y)\) \(0\) \(-3\) \((0,-3)\) \(\dfrac{3}{2}\) \(0\) \(\left(\dfrac{3}{2},0\right)\) The \(x\)-intercept is \(\left(\dfrac{3}{2},0\right)\).
The \(y\)-intercept is \((0,-3)\).
Graph the lines. 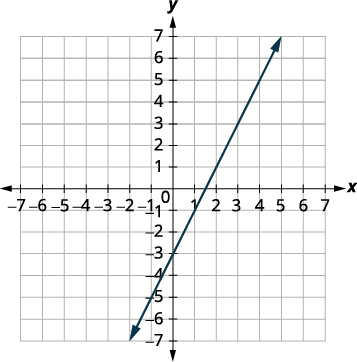
Determine the points of intersection. The lines are the same! Any point on the line is a point of intersection.
Since every point on the line, when substituted, makes both equations true, there are infinitely many ordered pairs that make both equations true.Answer the question. There are infinitely many solutions to the system. If we write the second equation in slope-intercept form, we may recognize that the equations have the same slope and same \(y\)-intercept.
Solve the system \(\left\{ \begin{array}{l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right.\) by graphing.
- Answer
-
The system has infinitely many solutions.
Solve the system \(\left\{ \begin{array}{l} y = \dfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right.\) by graphing.
- Answer
-
The system has infinitely many solutions.
When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident. Coincident lines have the same slope and same \(y\)-intercept.
Coincident lines have the same slope and same \(y\)-intercept.
The systems of equations in Example and Example each had two intersecting lines. Each system had one solution.
In Example, the equations gave coincident lines, and so the system had infinitely many solutions.
The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.
A system with parallel lines, like Example, has no solution. We call a system of equations like this inconsistent. It has no solution.
A consistent system of equations is a system of equations with at least one solution.
An inconsistent system of equations is a system of equations with no solution.
We also categorize the equations in a system of equations by calling the equations independent or dependent. If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines. Otherwise, they each have their own different set of solutions and we say the two equations are independent. Intersecting lines and parallel lines are independent.
Two equations are dependent if they have the same set of solutions. Two equations are independent if their solutions differ.
Let’s sum this up by looking at the graphs of the three types of systems. See below.
| Lines | Intersecting | Parallel | Coincident |
|---|---|---|---|
| Number of solutions | One point | No solution | Infinitely many |
| Consistent/Inconsistent | Consistent | Inconsistent | Consistent |
| Dependent/Independent | Independent | Independent | Dependent |
Solving systems of linear equations by graphing is a good way to visualize the types of solutions that may result. However, there are many cases where solving a system by graphing is inconvenient or imprecise. If the graphs extend beyond the small grid with \(x\) and \(y\) both between \(−10\) and \(10\), graphing the lines may be cumbersome. And if the solutions to the system are not integers, it can be hard to read their values precisely from a graph.
Solve a System of Equations by Substitution
We will now solve systems of linear equations by the substitution method.
We will use the same system we used first for graphing.
\[ \left\{ \begin{aligned} 2x+y&=7 \\ x−2y&=6 \end{aligned} \right. \nonumber \]
We will first solve one of the equations for either \(x\) or \(y\). We can choose either equation and solve for either variable - but we’ll try to make a choice that will keep the work easy.
Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!
After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it is a solution to both equations.
Solve the system \(\left\{ \begin{aligned} 2x+y&=7 \\ x−2y&=6 \end{aligned} \right.\) by substitution.
- Solution
-
\( \left\{ \begin{aligned} 2x+y&=7 \\ x−2y&=6 \end{aligned} \right. \) Solve one of the equations for either variable. We will solve the first equation for \(y\). \(\begin{aligned} 2x+y &= 7\\ y &=7-2x\end{aligned}\) Substitute the expression from the previous step into the other equation. We replace \(y\) in the second equation with the expression \(7-2x\). \(\begin{aligned} x-2y&= 6\\ x-2(7-2x) &=6\end{aligned}\) Solve the resulting equation. Now we have an equation with just one variable. We know how to solve this. \(\begin{aligned} x-14+4x &= 6 \\ 5x&= 20 \\ x &=4 \end{aligned}\) Substitute the solution just found into one of the original equations to find the other variable. We will use the first equation and replace \(x\) with \(4\). \(\begin{aligned} 2x+y &= 7\\ 2\cdot 4 +y&=7 \\8+y&=7 \\ y&=-1\end{aligned}\) Write the solution as an ordered pair. Write \(x=4\) and \(y=-1\) as an ordered pair. \((4,-1)\) Check that the ordered pair is a solution to both original equations. Substitute \(x=4\) and \(y=-1\) into both equations and make sure they are both true. \(\begin{aligned} 2x+y&=7 \\ 2 (4)+(-1) & \stackrel{?}{=} 7 \\ 7& \stackrel{?}{=} 7\\ & \quad\text{True}\end{aligned}\quad\quad\begin{aligned} x−2y&=6 \\ 4-2(-1) & \stackrel{?}{=} 6 \\6 & \stackrel{?}{=} 6 \\ &\quad \text{True}\end{aligned}\)
Substituting \((4,-1)\) in for \((x,y)\) makes both equations true.
Answer the question. \((4,-1)\) is a solution to the system.
Solve the system \( \left\{ \begin{array}{l} −2x+y =−11 \\ x+3y=9 \end{array} \right.\) by substitution.
- Answer
-
The solution is \((6,1)\).
Solve the system \( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right.\) by substitution.
- Answer
-
The solution is \((−3,5)\).
- Solve one of the equations for either variable.
- Substitute the expression from Step 1 into the other equation.
- Solve the resulting equation.
- Substitute the solution in Step 3 into either of the original equations to find the other variable.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations. This step is added here in order to check for errors.
Be very careful with the signs in the next example.
Solve the system \( \left\{ \begin{array}{l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \) by substitution.
- Solution
-
We need to solve one equation for one variable. We will solve the first equation for \(y\).
\( \left\{ \begin{array}{l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \) Solve the first equation for \(y\). \(\begin{aligned} 4x+2y &= 4\\ 2y &=-4x+4\\ y &= -2x+2\end{aligned}\)
Replace the \(y\) with \(−2x+2\) in the second equation. \(\begin{aligned} 6x-y &= 8\\ 6x-(-2x+2) &=8\end{aligned}\)
Solve the equation for \(x\). \(\begin{aligned} 6x+2x-2 &= 8 \\ 8x &=10 \\ x &= \dfrac{5}{4}\end{aligned}\)
Substitute \(x=\dfrac{5}{4}\) into \(4x+2y=4\) to find \(y\). \(\begin{aligned} 4x+2y &= 4 \\ 4\cdot \dfrac{5}{4} + 2y &= 4 \\ 5+2y &= 4\\ 2y &= -1 \\ y &= -\dfrac{1}{2}\end{aligned}\)
Write the solution as an ordered pair. The ordered pair is \(\left(\dfrac{5}{4},−\dfrac{1}{2}\right)\). Check the ordered pair in both equations.
\(\begin{aligned} 4x+2y&=4 \\ 4\left(\dfrac{5}{4}\right)+2\left(-\dfrac{1}{2}\right) & \stackrel{?}{=} 4 \\ 5-1& \stackrel{?}{=} 4\\ 4& \stackrel{?}{=} 4 \\ & \quad\text{True}\end{aligned}\quad\quad\begin{aligned} 6x-y&=8 \\ 6\left(\dfrac{5}{4}\right)-\left(-\dfrac{1}{2}\right) & \stackrel{?}{=} 8 \\ \dfrac{15}{4}+\dfrac{1}{2}& \stackrel{?}{=} 8\\ \dfrac{16}{2}& \stackrel{?}{=} 8 \\ 4& \stackrel{?}{=} 4\\ & \quad \text{True}\end{aligned}\)
Substituting \(\left(\dfrac{5}{4},−\dfrac{1}{2}\right)\) in for \((x,y)\) makes both equations true.
Answer the question. \(\left(\dfrac{5}{4},−\dfrac{1}{2}\right)\) is a solution to the system.
Solve the system \( \left\{\begin{array}{l}x−4y=−4 \\ −3x+4y=0 \end{array} \right. \) by substitution.
- Answer
-
The solution is \(\left(2,\dfrac{3}{2}\right)\).
Solve the system \( \left\{ \begin{array}{l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \) by substitution.
- Answer
-
The solution is \(\left(−\dfrac{1}{2},−2\right)\).
Solve a System of Equations by Elimination
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations with two variables and reduced it to one equation with one variable. This is what we will do with the elimination method, too, but we will get there a different way.
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when we add the same quantity to both sides of an equation, we still have equality. We will extend the Addition Property of Equality to say that when we add equal quantities to both sides of an equation, the results are equal. In other words, for any expressions \(a\), \(b\), \(c\), and \(d\),
\[\begin{array} {lrcl} {\text{if}} &a &=&b \\ {\text{and}} &c&=&d \\ {\text{then}} &a+c&=&b+d. \nonumber \end{array}\]
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]
\[\quad\quad \; 5x=5 \nonumber\]
The \(y\)’s add to zero and we have one equation with one variable.
Let’s try another one:
\[ \left\{ \begin{aligned} x+4y&=2 \\ 2x+5y&=−2 \end{aligned} \right. \nonumber\]
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by \(−2\), we will make the coefficients of \(x\) opposites. We must multiply every term on both sides of the equation by \(−2\).
\[ \left\{ \begin{aligned} (-2)(x+4y)&=(-2)2 \\ 2x+5y&=−2 \end{aligned} \right. \nonumber\]
Then rewrite the system of equations.
\[ \left\{ \begin{aligned} -2x-8y &=-4 \\ 2x+5y &=−2 \end{aligned} \right. \nonumber\]
Now we see that the coefficients of the \(x\) terms are opposites, so \(x\) will be eliminated when we add these two equations.
\[ \left\{ \begin{aligned} -2x-8y=-4 \\ \underline{2x+5y =−2} \end{aligned} \right. \nonumber\]
\[\quad\qquad -3y=-6 \nonumber\]
Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.
Now we will see how to use elimination to solve the same system of equations we solved by graphing and by substitution.
Solve the system \(\left\{\begin{array}{l} 2x+y=7 \\ x−2y=6 \end{array} \right. \) by elimination.
- Solution
-
\(\left\{\begin{array}{l} 2x+y=7 \\ x−2y=6 \end{array} \right. \) Write both equations in standard form.
- If any coefficients are fractions, clear them.
Both equations are in standard form, \(Ax+By=C\). There are no fractions \(\left\{\begin{array}{l} 2x+y=7 \\ x−2y=6 \end{array} \right. \) Make the coefficients of one variable opposites.
- Decide which variable you will eliminate.
- Multiply one of both equations so that the coefficients of that variable are opposites.
We can eliminate the \(y\)'s by multiplying the first equation by \(2\).
Multiply both sides of \(2x+y=7\) by \(2\).
\(\left\{\begin{aligned} 2(2x+y)&=2(7) \\ x−2y&=6 \end{aligned} \right. \) Add the equations resulting from the previous step to eliminate one variable. We add the \(x\)'s, \(y\)'s, and constants. \(\left\{\begin{array}{l} 4x+2y=14 \\ \;\;\underline{x−2y=6}\\\quad\quad 5x=20 \end{array} \right. \) Solve for the remaining variable. Solve for \(x\). \(x=4\)
Substitute the solution from the previous step into one of the original equations. Then solve for the other variable. Substitute \(x=4\) into the second equation, \(x-2y=6\). Then solve for \(y\). \(\begin{aligned}x-2y&= 6\\ 4-2y&= 6\\-2y&= 2\\ y&=-1\end{aligned}\) Write the solution as an ordered pair. Write it as \((x,y)\). \((4,-1)\) Check that the ordered pair is a solution to both original equations. Substitute \(x=4\), \(y=-1\) into \(2x+y=7\) and \(x-2y=6\). Do they make both equations true? \(\begin{aligned} 2x+y&=7 \\ 2(4)+(-1) & \stackrel{?}{=} 7 \\7 & \stackrel{?}{=} 7\\ &\quad \text{True}\end{aligned}\quad\quad\begin{aligned} x-2y&=6 \\ 4-2(-1) & \stackrel{?}{=} 6 \\6 & \stackrel{?}{=} 6 \\ &\quad \text{True}\end{aligned}\)
Substituting \((x,y)=(4,-1)\) makes both equations true.
Answer the question. The solution is \((4,-1)\)
Solve the system \(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\) by elimination.
- Answer
-
The solution is \((2,−1)\).
Solve the system \(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\) by elimination.
- Answer
-
The solution is \((−2,3)\).
The steps are listed here for easy reference.
- Write both equations in standard form. If any coefficients are fractions, clear them.
- Make the coefficients of one variable opposites.
- Decide which variable you will eliminate.
- Multiply one or both equations by appropriate numbers so that the coefficients of that variable are opposites.
- Add the equations resulting from Step 2 to eliminate one variable.
- Solve for the remaining variable.
- Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Write the solution as an ordered pair.
- Check that the ordered pair is a solution to both original equations. This step is included for the purpose of detecting errors.
Now we will do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.
Solve the system \(\left\{ \begin{array}{l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \) by elimination.
- Solution
-
In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.
\(\left\{ \begin{array}{l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \) Both equations are in standard form.
To get opposite coefficients of \(y\), we will
multiply the first equation by \(2\) and the
second equation by \(3\).\(\left\{ \begin{aligned} 2(4x−3y)&=2(9) \\ 3(7x+2y)&=3(−6) \end{aligned} \right. \) Simplify. \(\left\{ \begin{aligned} 8x−6y&=18 \\ 21x+6y&=-18 \end{aligned} \right.\) Add the two equations to eliminate \(y\). \(29x=0\) Solve for \(x\). \(x=0\) Substitute \(x=0\) into one of the original equations. \(\begin{aligned} 7x+2y&=−6 \\ 7(0)+2y&=-6\end{aligned}\) Simplify. \(2y=-6\) Solve for \(y\). \(y=-3\) Check that the ordered pair is a solution to
both original equations.\(\begin{aligned} 4x-3y&=9 \\ 4(0)-3(-3) & \stackrel{?}{=} 9 \\9 & \stackrel{?}{=} 9\\ &\quad \text{True}\end{aligned}\quad\quad\begin{aligned} 7x+2y&=-6 \\ 7(0)+2(-3) & \stackrel{?}{=} -6 \\-6 & \stackrel{?}{=} -6 \\ &\quad \text{True}\end{aligned}\)
Substituting \((x,y)=(0,-3)\) makes both equations true.
Answer the question. The solution is \((0,-3)\).
Solve the system \(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \) by elimination.
- Answer
-
The solution is \((1,3)\).
Solve the system \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\) by elimination.
- Answer
-
The solution is \((4,−3)\).
When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.
Solve the system \(\left\{ \begin{array}{l} x+\dfrac{1}{2}y =6 \\ \dfrac{3}{2}x+\dfrac{2}{3}y=\dfrac{17}{2} \end{array} \right.\) by elimination.
- Solution
-
In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.
\(\left\{ \begin{aligned} x+\dfrac{1}{2}y &=6 \\ \dfrac{3}{2}x+\dfrac{2}{3}y&=\dfrac{17}{2} \end{aligned} \right.\) To clear the fractions, multiply each
equation by its LCD.\(\left\{ \begin{aligned}2\left( x+\dfrac{1}{2}y\right) &=2(6) \\ 6\left(\dfrac{3}{2}x+\dfrac{2}{3}y\right)&=6\left(\dfrac{17}{2}\right) \end{aligned} \right.\)
Simplify \(\left\{ \begin{aligned} 2x+y &=12 \\ 9x+4y&=51 \end{aligned} \right.\) Now we are ready to eliminate one of the variables. Notice that both equations are in
standard form.We can eliminate \(y\) by multiplying the top equation by \(−4\).
\(\left\{ \begin{aligned} -4(2x+y) &=-4(12) \\ 9x+4y&=51 \end{aligned} \right.\) Simplify. \(\left\{ \begin{aligned}-8x-4y&= -48 \\ 9x+4y&=51\end{aligned}\right.\) Add. \(x=3\) Substitute \(x=3\) into one of the original equations. \(\begin{aligned} x+\dfrac{1}{2}y &=6 \\3+\dfrac{1}{2}y &=6\end{aligned}\) Simplify. \(\dfrac{1}{2}y = 3\) Solve for \(y\). \(y=6\) Write the solution as an ordered pair. The ordered pair is \((3,6)\). Check that the ordered pair is a solution to
both original equations.\(\begin{aligned} x+\dfrac{1}{2}y&=6 \\3+\dfrac{1}{2}(6) & \stackrel{?}{=} 6 \\3+3 & \stackrel{?}{=} 6 \\ 6&\stackrel{?}{=} 6 \\ & \quad \text{True}\end{aligned}\quad\quad\begin{aligned} \dfrac{3}{2}x+\dfrac{2}{3}y&\stackrel{?}{=} \dfrac{17}{2} \\ \dfrac{3}{2}(3)+\dfrac{2}{3}(6)&\stackrel{?}{=} \dfrac{17}{2} \\ \dfrac{9}{2}+4 &\stackrel{?}{=} \dfrac{17}{2} \\ \dfrac{9}{2}+\dfrac{8}{2} &\stackrel{?}{=} \dfrac{17}{2} \\ \dfrac{17}{2}&\stackrel{?}{=} \dfrac{17}{2} \\ &\quad \text{True}\end{aligned}\)
Substituting \((x,y)=(3,6)\) makes both equations true.
Answer the question. The solution is \((3,6)\).
Solve the system \(\left\{ \begin{array} {l} \dfrac{1}{3}x−\dfrac{1}{2}y=1 \\ \dfrac{3}{4}x−y=\dfrac{5}{2} \end{array} \right.\) by elimination.
- Answer
-
The solution is \((6,2)\).
Solve the system \(\left\{ \begin{array} {l} x+\dfrac{3}{5}y=−\dfrac{1}{5} \\ −\dfrac{1}{2}x−\dfrac{2}{3}y=\dfrac{5}{6} \end{array} \right.\) by elimination.
- Answer
-
The solution is \((1,−2)\).
When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.
The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.
Solve the system \(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\dfrac{3}{4}x \end{array} \right. \) by elimination.
- Solution
-
\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\dfrac{3}{4}x \end{array} \right.\) Write the second equation in standard form. \(\left\{ \begin{array} {l} 3x+4y=12 \\ \dfrac{3}{4}x+y=3 \end{array} \right.\) Clear the fractions by multiplying the second equation by \(4\). \(\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\dfrac{3}{4}x+y)=4(3) \end{array} \right.\) Simplify. \(\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right.\) To eliminate a variable, we multiply the second equation by \(−1\) and simplify. \(\left\{\begin{array} {l} 3x+4y=12 \\ -3x-4y=-12\end{array}\right.\) Add the equations. \(0=0\) Conclusion. This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. Answer the question. The system has infinitely many solutions. After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.
Solve the system \(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\dfrac{5}{3}x \end{array} \right. \) by elimination.
- Answer
-
The system has infinitely many solutions.
Solve the system \(\left\{ \begin{array} {l} x+2y=6 \\ y=−\dfrac{1}{2}x+3\end{array} \right. \) by elimination.
- Answer
-
The system has infinitely many solutions.
Choose the Most Convenient Method to Solve a System of Linear Equations
When we solve a system of linear equations in an application, we will not be told which method to use. We will need to make that decision ourselves. So we will want to choose the method that is easiest to do and minimizes our chance of making mistakes.
| Choose the Most Convenient Method to Solve a System of Linear Equations | ||
|---|---|---|
| Graphing | Substitution | Elimination |
| Use when you need a picture of the situation. | Use when one equation is already solved or can be easily solved for one variable. | Use when the equations are in standard form. |
For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
a. \(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\)
b. \(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\dfrac{2}{3}x−1 \end{array} \right.\)
- Solution
-
a.
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]
Since both equations are in standard form, using elimination will be most convenient.
b.
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\dfrac{2}{3}x−1 \end{array} \right.\nonumber \]
Since one equation is already solved for \(y\), using substitution will be most convenient (especially since we see that the fraction will be reduced to an integer in the first step of simplification).
\(\PageIndex{40}\)
For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
a. \(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\)
b. \(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)
- Answer
-
a. Since both equations are in standard form, using elimination will be most convenient.
b. Since one equation is already solved for \(x\), using substitution will be most convenient.
\(\PageIndex{41}\)
For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.
a. \(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\)
b. \(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)
- Answer
-
a. Since one equation is already solved for \(y\), using substitution will be most convenient.
b. Since both equations are in standard form, using elimination will be most convenient.
Key Concepts
- How to solve a system of linear equations by graphing.
- Graph the first equation.
- Graph the second equation on the same rectangular coordinate system.
- Determine whether the lines intersect, are parallel, or are the same line.
- Identify the solution to the system.
If the lines intersect, identify the point of intersection. This is the solution to the system.
If the lines are parallel, the system has no solution.
If the lines are the same, the system has an infinite number of solutions. - Check the solution in both equations. This step is included to make sure there was no error and that the intersection point was correctly identified.
- How to solve a system of equations by substitution.
- Solve one of the equations for either variable.
- Substitute the expression from Step 1 into the other equation.
- Solve the resulting equation.
- Substitute the solution in Step 3 into either of the original equations to find the other variable.
- Write the solution as an ordered pair.
- In order to detect errors, check that the ordered pair is a solution to both original equations.
- How to solve a system of equations by elimination.
- Write both equations in standard form. If any coefficients are fractions, clear them.
- Make the coefficients of one variable opposites.
Decide which variable you will eliminate.
Multiply one or both equations by appropriate numbers so that the coefficients of that variable are opposites. - Add the equations resulting from Step 2 to eliminate one variable.
- Solve for the remaining variable.
- Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
- Write the solution as an ordered pair.
- In order to detect errors, check that the ordered pair is a solution to both original equations. \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
Glossary
- coincident lines
- Coincident lines have the same slope and same y-intercept.
- consistent and inconsistent systems
- Consistent system of equations is a system of equations with at least one solution; inconsistent system of equations is a system of equations with no solution.
- solutions of a system of equations
- Solutions of a system of equations are the values of the variables that make all the equations true; solution is represented by an ordered pair \((p,q)\).
- system of linear equations
- When two or more linear equations are grouped together, they form a system of linear equations.
Practice Makes Perfect
Determine Whether an Ordered Pair is a Solution of a System of Equations
In the following exercises, determine if the following points are solutions to the given system of equations.
1. \(\left\{ \begin{array} {l} 2x−6y=0 \\ 3x−4y=5 \end{array} \right.\)
ⓐ \((3,1)\)
ⓑ \((−3,4)\)
- Answer
-
ⓐ yes ⓑ no
2. \(\left\{ \begin{array} {l} −3x+y=8 \\ −x+2y=−9 \end{array} \right.\)
ⓐ \((−5,−7)\)
ⓑ \((−5,7)\)
3. \(\left\{ \begin{array} {l} x+y=2 \\ y=\dfrac{3}{4}x \end{array} \right.\)
ⓐ \((87,67)\)
ⓑ \((1,34)\)
- Answer
-
ⓐ yes ⓑ no
4. \(\left\{ \begin{array} {l} 2x+3y=6 \\ y=\dfrac{2}{3}x+2 \end{array} \right.\)
ⓐ \((−6,2)\)
ⓑ \((−3,4)\)
Solve a System of Linear Equations by Graphing
In the following exercises, solve the following systems of equations by graphing.
5. \(\left\{ \begin{array} {l} 3x+y=−3 \\ 2x+3y=5 \end{array} \right.\)
- Answer
-
\((−3,2)\)
6. \(\left\{ \begin{array} {l} −x+y=2 \\ 2x+y=−4 \end{array} \right.\)
7. \(\left\{ \begin{array} {l} y=x+2 \\ y=−2x+2 \end{array} \right.\)
- Answer
-
\((0,2)\)
8. \(\left\{ \begin{array} {l} y=x−2 \\ y=−3x+2 \end{array} \right.\)
9. \(\left\{ \begin{array} {l} y=\dfrac{3}{2}x+1 \\ y=−\dfrac{1}{2}x+5 \end{array} \right.\)
- Answer
-
\((2,4)\)
10. \(\left\{ \begin{array} {l} y=\dfrac{2}{3}x−2 \\ y=−\dfrac{1}{3}x−5 \end{array} \right.\)
11. \(\left\{ \begin{array} {l} x+y=−4 \\ −x+2y=−2 \end{array} \right.\)
- Answer
-
\((−2,2)\)
12. \(\left\{ \begin{array} {l} −x+3y=3 \\ x+3y=3 \end{array} \right.\)
13. \(\left\{ \begin{array} {l} −2x+3y=3 \\ x+3y=12 \end{array} \right.\)
- Answer
-
\((3,3)\)
14. \(\left\{ \begin{array} {l} 2x−y=4 \\ 2x+3y=12 \end{array} \right.\)
15. \(\left\{ \begin{array} {l} x+3y=−6 \\ y=−\dfrac{4}{3}x+4 \end{array} \right.\)
- Answer
-
\((6,−4)\)
16. \(\left\{ \begin{array} {l} −x+2y=−6 \\ y=−\dfrac{1}{2}x−1 \end{array} \right.\)
17. \(\left\{ \begin{array} {l} −2x+4y=4 \\ y=\dfrac{1}{2}x \end{array} \right.\)
- Answer
-
no solution
18. \(\left\{ \begin{array} {l} 3x+5y=10 \\ y=−\dfrac{3}{5}x+1 \end{array} \right.\)
19. \(\left\{ \begin{array} {l} 4x−3y=8 \\ 8x−6y=14 \end{array} \right.\)
- Answer
-
no solution
20. \(\left\{ \begin{array} {l} x+3y=4 \\ −2x−6y=3 \end{array} \right.\)
21. \(\left\{ \begin{array} {l} x=−3y+4 \\ 2x+6y=8 \end{array} \right.\)
- Answer
-
infinite solutions with solution set: \(\big\{ (x,y) | 2x+6y=8 \big\}\)
22. \(\left\{ \begin{array} {l} 4x=3y+7 \\ 8x−6y=14 \end{array} \right.\)
23. \(\left\{ \begin{array} {l} 2x+y=6 \\ −8x−4y=−24 \end{array} \right.\)
- Answer
-
infinite solutions with solution set: \(\big\{ (x,y) | 2x+y=6 \big\}\)
24. \(\left\{ \begin{array} {l} 5x+2y=7 \\ −10x−4y=−14 \end{array} \right.\)
Without graphing, determine the number of solutions and then classify the system of equations.
25. \(\left\{ \begin{array} {l} y=\dfrac{2}{3}x+1 \\ −2x+3y=5 \end{array} \right.\)
- Answer
-
1 point, consistent and independent
26. \(\left\{ \begin{array} {l} y=\dfrac{3}{2}x+1 \\ 2x−3y=7 \end{array} \right.\)
27. \(\left\{ \begin{array} {l} 5x+3y=4 \\ 2x−3y=5 \end{array} \right.\)
- Answer
-
1 point, consistent and independent
28. \(\left\{ \begin{array} {l} y=−12x+5 \\ x+2y=10 \end{array} \right.\)
29. \(\left\{ \begin{array} {l} 5x−2y=10 \\ y=52x−5 \end{array} \right.\)
- Answer
-
infinite solutions, consistent, dependent
Solve a System of Equations by Substitution
In the following exercises, solve the systems of equations by substitution.
30. \(\left\{ \begin{array} {l} 2x+y=−4 \\ 3x−2y=−6\end{array} \right.\)
31. \(\left\{ \begin{array} {l} 2x+y=−2\\ 3x−y=7 \end{array} \right.\)
- Answer
-
\((1,−4)\)
32. \(\left\{ \begin{array} {l} x−2y=−5 \\ 2x−3y=−4 \end{array} \right.\)
33. \(\left\{ \begin{array} {l} x−3y=−9 \\ 2x+5y=4 \end{array} \right.\)
- Answer
-
\((−3,2)\)
34. \(\left\{ \begin{array} {l} 5x−2y=−6 \\ y=3x+3 \end{array} \right.\)
35. \(\left\{ \begin{array} {l} −2x+2y=6 \\ y=−3x+1 \end{array} \right.\)
- Answer
-
\((−1/2,5/2)\)
36. \(\left\{ \begin{array} {l} 2x+5y=1 \\ y=\dfrac{1}{3}x−2 \end{array} \right.\)
37. \(\left\{ \begin{array} {l} 3x+4y=1 \\ y=−\dfrac{2}{5}x+2 \end{array} \right.\)
- Answer
-
\((−5,4)\)
38. \(\left\{ \begin{array} {l} 2x+y=5 \\ x−2y=−15 \end{array} \right.\)
39. \(\left\{ \begin{array} {l} 4x+y=10 \\ x−2y=−20 \end{array} \right.\)
- Answer
-
\((0,10)\)
40. \(\left\{ \begin{array} {l} y=−2x−1 \\ y=−\dfrac{1}{3}x+4 \end{array} \right.\)
41. \(\left\{ \begin{array} {l} y=x−6 \\ y=−\dfrac{3}{2}x+4 \end{array} \right.\)
- Answer
-
\((4,−2)\)
42. \(\left\{ \begin{array} {l} x=2y \\ 4x−8y=0 \end{array} \right.\)
43. \(\left\{ \begin{array} {l} 2x−16y=8 \\ −x−8y=−4 \end{array} \right.\)
- Answer
-
\((4,0)\)
44. \(\left\{ \begin{array} {l} y=\dfrac{7}{8}x+4 \\ −7x+8y=6 \end{array} \right.\)
45. \(\left\{ \begin{array} {l} y=−\dfrac{2}{3}x+5 \\ 2x+3y=11 \end{array} \right.\)
- Answer
-
no solution
Solve a System of Equations by Elimination
In the following exercises, solve the systems of equations by elimination.
46. \(\left\{ \begin{array} {l} 5x+2y=2 \\ −3x−y=0 \end{array} \right.\)
47. \(\left\{ \begin{array} {l} 6x−5y=−1 \\ 2x+y=13 \end{array} \right.\)
- Answer
-
\((4,5)\)
48. \(\left\{ \begin{array} {l} 2x−5y=7 \\ 3x−y=17 \end{array} \right.\)
49. \(\left\{ \begin{array} {l} 5x−3y=−1 \\ 2x−y=2 \end{array} \right.\)
- Answer
-
\((7,12)\)
50. \(\left\{ \begin{array} {l} 3x−5y=−9 \\ 5x+2y=16 \end{array} \right.\)
51. \(\left\{ \begin{array} {l} 4x−3y=3 \\ 2x+5y=−31 \end{array} \right.\)
- Answer
-
\((−3,−5)\)
52. \(\left\{ \begin{array} {l} 3x+8y=−3 \\ 2x+5y=−3 \end{array} \right.\)
53. \(\left\{ \begin{array} {l} 11x+9y=−5 \\ 7x+5y=−1 \end{array} \right.\)
- Answer
-
\((2,−3)\)
54. \(\left\{ \begin{array} {l} 3x+8y=67 \\ 5x+3y=60 \end{array} \right.\)
55. \(\left\{ \begin{array} {l} 2x+9y=−4 \\ 3x+13y=−7 \end{array} \right.\)
- Answer
-
\((−11,2)\)
56. \(\left\{ \begin{array} {l} \dfrac{1}{3}x−y=−3 \\ x+\dfrac{5}{2}y=2 \end{array} \right.\)
57. \(\left\{ \begin{array} {l} x+\dfrac{1}{2}y=\dfrac{3}{2} \\ \dfrac{1}{5}x−\dfrac{1}{5}y=3 \end{array} \right.\)
- Answer
-
\((6/−9,24/7)\)
58. \(\left\{ \begin{array} {l} x+\dfrac{1}{3}y=−1 \\ \dfrac{1}{3}x+\dfrac{1}{2}y=1 \end{array} \right.\)
59. \(\left\{ \begin{array} {l} \dfrac{1}{3}x−y=−3 \\ \dfrac{2}{3}x+\dfrac{5}{2}y=3 \end{array} \right.\)
- Answer
-
\((−3,2)\)
60. \(\left\{ \begin{array} {l} 2x+y=3 \\ 6x+3y=9 \end{array} \right.\)
61. \(\left\{ \begin{array} {l} x−4y=−1 \\ −3x+12y=3 \end{array} \right.\)
- Answer
-
infinitely many solutions with solution set: \(\big\{ (x,y) | x−4y=−1 \big\}\)
62. \(\left\{ \begin{array} {l} −3x−y=8 \\ 6x+2y=−16 \end{array} \right.\)
63. \(\left\{ \begin{array} {l} 4x+3y=2 \\ 20x+15y=10 \end{array} \right.\)
- Answer
-
infinitely many solutions with solution set: \(\big\{ (x,y) | 4x+3y=2 \big\}\)
Choose the Most Convenient Method to Solve a System of Linear Equations
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
64.
ⓐ \(\left\{ \begin{array} {l} 8x−15y=−32 \\ 6x+3y=−5 \end{array} \right.\)
ⓑ \(\left\{ \begin{array} {l} x=4y−3 \\ 4x−2y=−6 \end{array} \right.\)
65.
ⓐ \(\left\{ \begin{array} {l} y=7x−5 \\ 3x−2y=16 \end{array} \right.\)
ⓑ \(\left\{ \begin{array} {l} 12x−5y=−42 \\ 3x+7y=−15 \end{array} \right.\)
- Answer
-
ⓐ substitution ⓑ elimination
66.
ⓐ \(\left\{ \begin{array} {l} y=4x+95 \\ x−2y=−21 \end{array} \right.\)
ⓑ \(\left\{ \begin{array} {l} 9x−4y=24 \\ 3x+5y=−14 \end{array} \right.\)
67.
ⓐ \(\left\{ \begin{array} {l} 14x−15y=−30 \\ 7x+2y=10 \end{array} \right.\)
ⓑ \(\left\{ \begin{array} {l} x=9y−11 \\ 2x−7y=−27 \end{array} \right.\)
- Answer
-
ⓐ elimination ⓑ substitution
Writing Exercises
68. In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.
69. Solve the system of equations by substitution and explain all your steps in words: \(\left\{ \begin{array} {l} 3x+y=1 \\ 2x=y−8 \end{array} \right. \)
- Answer
-
Answers will vary.
70. Solve the system of equations by elimination and explain all your steps in words: \(\left\{ \begin{array} {l} 5x+4y=10 \\ 2x=3y+27 \end{array} \right. \)
71. Solve the system of equations \(\left\{ \begin{array} {l} x+y=10 \\ x−y=6 \end{array} \right.\)
ⓐ by graphing ⓑ by substitution
ⓒ Which method do you prefer? Why?
- Answer
-
Answers will vary.
Self Check
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.