7.4: Applications of Quadratic Equations
- Page ID
- 67019
By the end of this section, you will be able to:
- Solve applications modeled by quadratic equations
Before you get started, take this readiness quiz.
- The sum of two consecutive odd numbers is \(−100\). Find the numbers.
- Solve \(\dfrac{2}{x+1}+\dfrac{1}{x-1}=\dfrac{1}{x^{2}-1}\).
- Find the length of the hypotenuse of a right triangle with legs \(5\) inches and \(12\) inches.
Solve Applications Modeled by Quadratic Equations
We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications.
Let’s first summarize the methods we now have to solve quadratic equations.
- Factoring
- Square Root Property
- Completing the Square
- Quadratic Formula
As we solve each equation, we choose the method that is most convenient for us to work the problem. As a reminder, we will copy our usual Problem-Solving Strategy here so we can follow the steps.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
We have solved a number of applications that involved consecutive even and odd integers, by modeling the situation with linear equations. Remember, we noticed each even integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.
\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)
\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)
Some applications of odd or even consecutive integers are modeled by quadratic equations. The notation above will be helpful as we name the variables.
The product of two consecutive odd integers is \(195\). Find the integers.
- Solution
-
Read the problem. Identify what we are looking for. We are looking for two consecutive odd integers. Name what we are looking for. Let \(n=\) the first odd integer.
Then (n+2=\) the next odd integer.
Translate into an equation. State the problem in one sentence. “The product of two consecutive odd integers is \(195\).”
The product of the first odd integer and the second odd integer is \(195\).
Translate into an equation. \(n(n+2)=195\) Solve the equation. Distribute. \(n^{2}+2 n=195\) Write the equation in standard form. \(n^{2}+2 n-195=0\) Factor. \((n+15)(n-13)=0\) Use the Zero Product Property. \(n+15=0 \quad\) or \(\quad n-13=0\) Solve each equation. \(n=-15\quad\) or \(\quad n=13\) There are two values of \(n\) that are solutions. This will give us two pairs of consecutive odd integers for our solution. \(\begin{array}{cc}{\text { First odd integer: } n=-15} & {\qquad\text { First odd integer: } n=13} \\ {\text { Next odd integer } } & \qquad{\text { Next odd integer } } \\ \begin{aligned}& n+2\\ =&-15+2\\=& -13\end{aligned} & \begin{aligned}& n+2\\ =&13+2\\=& 15\end{aligned}\end{array}\) Check the answer.
Do these pairs work? Are they consecutive odd integers?
\(\bullet\quad -15,-13\) are consecutive odd integers. Is their product \(195\)? Yes:
\(-13(-15) =195\)
\(\bullet\quad 13, 15\) are consecutive odd integers. Is their product \(195\)? Yes:
\(13\cdot 15 =195\)
Answer the question. Two consecutive odd integers whose product is \(195\) are \(-15,-13\) and \(13,15\).
The product of two consecutive odd integers is \(99\). Find the integers.
- Answer
-
The two consecutive odd integers whose product is \(99\) are \(9, 11\), and \(−9, −11\).
The product of two consecutive even integers is \(168\). Find the integers.
- Answer
-
The two consecutive even integers whose product is \(128\) are \(12, 14\) and \(−12, −14\).
We will use the formula for the area of a triangle to solve the next example.
For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\dfrac{1}{2} b h\).
Recall that when we solve geometric applications, it is helpful to draw the figure.
An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can only have an area of \(120\) square feet and the architect wants the base to be \(4\) feet more than twice the height. Find the base and height of the window.
- Solution
-
Read the problem. Draw a picture. 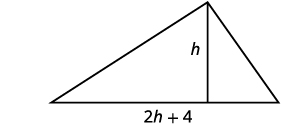
Identify what we are looking for. We are looking for the base and height. Name what we are looking for. Let \(h=\) the height of the triangle.
Then \(2h+4=\) the base of the triangle.
Translate into an equation.
We know the area. Write the formula for the area of a triangle.
\(A=\dfrac{1}{2} b h\) Solve the equation. Substitute in the values. \(120=\dfrac{1}{2}(2 h+4) h\) Distribute. \(120=h^{2}+2 h\) This is a quadratic equation, rewrite it in standard form. \(h^{2}+2 h-120=0\) Factor. \((h-10)(h+12)=0\) Use the Zero Product Property. \(h-10=0 \quad h+12=0\) Simplify. \(h=10, \quad \cancel{h=-12}\) Since \(h\) is the height of a window, a value of \(h=-12\) does not make sense. The height of the triangle \(h=10\). The base of the triangle \(2h+4\).
\(2 \cdot 10+4\)
\(24\)
Check the answer.
Does a triangle with height \(10\) and base \(24\) have area \(120\)? Yes.
Answer the question. The height of the triangular window is \(10\) feet and the base is \(24\) feet.
Find the base and height of a triangle whose base is four inches more than six times its height and has an area of \(456\) square inches.
- Answer
-
The height of the triangle is \(12\) inches and the base is \(76\) inches.
If a triangle that has an area of \(110\) square feet has a base that is two feet less than twice the height, what is the length of its base and height?
- Answer
-
The height of the triangle is \(11\) feet and the base is \(20\) feet.
In the two preceding examples, the number in the radical in the Quadratic Formula was a perfect square and so the solutions were rational numbers. If we get an irrational number as a solution to an application problem, we will use a calculator to get an approximate value.
We will use the formula for the area of a rectangle to solve the next example.
For a rectangle with length, \(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).
Mike wants to put \(150\) square feet of artificial turf in his front yard. This is the maximum area of artificial turf allowed by his homeowners association. He wants to have a rectangular area of turf with length one foot less than \(3\) times the width. Find the length and width. Round to the nearest tenth of a foot.
- Solution
-
Read the problem. Draw a picture. 
Identify what we are looking for. We are looking for the length and width. Name what we are looking for. Let \(W=\) the width of the rectangle.
Then \(3W-1=\) the length of the rectangle
Translate into an equation. We know the area. Write the formula for the area of a rectangle. \(A=L\cdot W\)
Solve the equation. Substitute in the values. \(150=(3W-1)W\)
Distribute. \(150=3W^2-W\)
This is a quadratic equation; rewrite it in standard form.
Solve the equation using the Quadratic Formula.
\(\underbrace{3W^2-W-150=0}_{ax^2+bx+c=0}\)
Identify the \(a,b,c\) values. \(a=3\)
\(b=-1\)
\(c=-150\)
Write the Quadratic Formula. \(W=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Then substitute in the values of \(a,b,c\). \(W=\dfrac{-(-1)\pm\sqrt{(-1)^2-4\cdot 3\cdot (-150)}}{2\cdot 3}\)
Simplify. \(W=\dfrac{1\pm\sqrt{1+1800}}{6}\)
\(W=\dfrac{1\pm\sqrt{1801}}{6}\)
Rewrite to show two solutions. \(W=\dfrac{1+\sqrt{1801}}{6},\quad \dfrac{1-\sqrt{1801}}{6}\)
Approximate the answers using a calculator.
We eliminate the negative solution for the width.
Check the answer. Make sure that the answers make sense. Since the answers are approximate, the area will not come out exactly to \(150\). Answer the question. The width of the rectangle is approximately \(7.2\) feet and the length is approximately \(20.6\) feet.
The length of a \(200\) square foot rectangular vegetable garden is four feet less than twice the width. Find the length and width of the garden, to the nearest tenth of a foot.
- Answer
-
The length of the garden is approximately \(18\) feet and the width \(11\) feet.
A rectangular tablecloth has an area of \(80\) square feet. The width is \(5\) feet shorter than the length.What are the length and width of the tablecloth to the nearest tenth of a foot?
- Answer
-
The length of the tablecloth is approximately \(11.8\) feet and the width \(6.8\) feet.
The Pythagorean Theorem gives the relation between the legs and hypotenuse of a right triangle. We will use the Pythagorean Theorem to solve the next example.
In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, \(a^{2}+b^{2}=c^{2}\).
Rene is setting up a holiday light display. He wants to make a ‘tree’ in the shape of two right triangles, as shown below, and has two \(10\)-foot strings of lights to use for the sides. He will attach the lights to the top of a pole and to two stakes on the ground. He wants the height of the pole to be the same as the distance from the base of the pole to each stake. How tall should the pole be?
- Solution
-
Read the problem. Draw a picture. 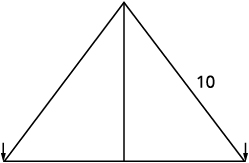
Identify what we are looking for. We are looking for the height of the pole. Name what we are looking for. The distance from the base of the pole to either stake is the same as the height of the pole.
Let \(x=\) the height of the pole.
Then \(x=\) the distance from pole to stakeEach side is a right triangle. We draw a picture of one of them.
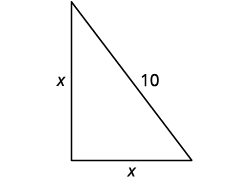
Translate into an equation.
We can use the Pythagorean Theorem to solve for \(x\).
Write the Pythagorean Theorem.\(a^{2}+b^{2}=c^{2}\) Solve the equation. Substitute. \(x^{2}+x^{2}=10^{2}\) Simplify. \(2 x^{2}=100\) Divide by \(2\) to isolate the variable. \(\dfrac{2 x^{2}}{2}=\dfrac{100}{2}\) Simplify. \(x^{2}=50\) Use the Square Root Property. \(x=\pm \sqrt{50}\) Simplify the radical. \(x=\pm 5 \sqrt{2}\) Rewrite to show two solutions. \(x=5 \sqrt{2}\quad \) or \(\quad x=\cancel{-5 \sqrt{2}}\) If we approximate \(x=5 \sqrt{2}\) to the nearest tenth with a calculator, we find \(x≈7.1\). Check the answer. Check on your own in the Pythagorean Theorem. Answer the question. The pole should be about \(7.1\) feet tall.
The sun casts a shadow from a flag pole. The height of the flag pole is three times the length of its shadow. The distance between the end of the shadow and the top of the flag pole is \(20\) feet. Find the length of the shadow and the length of the flag pole. Round to the nearest tenth.
- Answer
-
The length of the flag pole’s shadow is approximately \(6.3\) feet and the height of the flag pole is \(18.9\) feet.
The distance between opposite corners of a rectangular field is four more than the width of the field. The length of the field is twice its width. Find the distance between the opposite corners. Round to the nearest tenth.
- Answer
-
The distance between the opposite corners is approximately \(7.2\) feet.
OPTIONAL APPLICATIONS
The height of a projectile shot upward from the ground is modeled by a quadratic equation. The initial velocity, \(v_{0}\), propels the object up until gravity causes the object to fall back down.
The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula
\(h=-16 t^2+v_0 t\).
We can use this formula to find how many seconds it will take for a firework to reach a specific height.
A firework is shot upwards with initial velocity \(130\) feet per second. How many seconds will it take to reach a height of \(260\) feet? Round to the nearest tenth of a second.
- Solution
-
Read the problem. Identify what we are looking for. We are looking for the number of seconds, which is time. Name what we are looking for. Let \(t=\) the number of seconds. Translate into an equation. Use the formula. \(h=-16t^2+v_0t\)\) Solve the equation. We know the velocity \(v_{0}\) is \(130\) feet per second. The height is \(260\) feet. Substitute the values. \(260=-16t^2+130t\) This is a quadratic equation, rewrite it in standard form. Solve the equation using the Quadratic Formula. \(\underbrace{16t^2-130t+260=0}_{\color{red}{ax^2+bx+c=0}}\)
Identify the values of \(a, b, c\). \(a=16\)
\(b=-130\)
\(c=260\)
Write the Quadratic Formula. \(t=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) Then substitute in the values of \(a,b,c\). 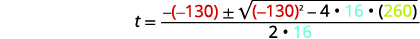
\(t=\dfrac{-(-130)\pm\sqrt{(-130)^2-4\cdot 16\cdot 260}}{2\cdot 16}\)
Simplify. \(t=\dfrac{130\pm\sqrt{16,900-16,640}}{32}\)
\(t=\dfrac{130\pm\sqrt{260}}{32}\)
Rewrite to show two solutions. \(t=\dfrac{130+\sqrt{260}}{32}, \qquad t=\dfrac{130-\sqrt{260}}{32}\) Approximate the answer with a calculator. \(t\approx 4.6 \) seconds
\(t\approx 3.6 \) seconds
Check the answer. The check is left to you. Answer the question. The firework will go up and then fall back down. As the firework goes up, it will reach \(260\) feet after approximately \(3.6\) seconds. It will also pass that height on the way down at \(4.6\) seconds.
An arrow is shot from the ground into the air at an initial speed of \(108\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the arrow will be \(180\) feet from the ground. Round the nearest tenth.
- Answer
-
The arrow will reach \(180\) feet on its way up after \(3\) seconds and again on its way down after approximately \(3.8\) seconds.
A man throws a ball into the air with a velocity of \(96\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the height of the ball will be \(48\) feet. Round to the nearest tenth.
- Answer
-
The ball will reach \(48\) feet on its way up after approximately \(.6\) second and again on its way down after approximately \(5.4\) seconds.
We have solved uniform motion problems using the formula \(D=rt\) in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

The formula \(D=rt\) assumes we know \(r\) and \(t\) and use them to find \(D\). If we know \(D\) and \(r\) and need to find \(t\), we would solve the equation for \(t\) and get the formula \(t=\dfrac{D}{r}\).
Some uniform motion problems are also modeled by quadratic equations.
Professor Smith just returned from a conference that was \(2,000\) miles east of his home. His total time in the airplane for the round trip was \(9\) hours. If the plane was flying at a rate of \(450\) miles per hour, what was the speed of the jet stream?
- Solution
-
This is a uniform motion situation. A diagram will help us visualize the situation.

Figure 9.5.30 We fill in the chart to organize the information.
We are looking for the speed of the jet stream. Let \(r=\) the speed of the jet stream.
When the plane flies with the wind, the wind increases its speed and so the rate is \(450 + r\).
When the plane flies against the wind, the wind decreases its speed and the rate is \(450 − r\).
Write in the rates.
Write in the distances.
Since \(D=r⋅t\), we solve for
\(t\) and get \(t=\dfrac{D}{r}\).
We divide the distance by
the rate in each row, and
place the expression in the
time column.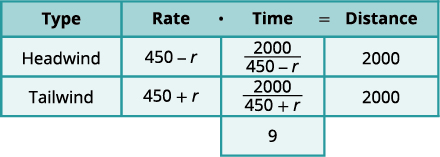
We know the times add to \(9\)
and so we write our equation.\(\dfrac{2000}{450-r}+\dfrac{2000}{450+r}=9\) We multiply both sides by the LCD. \((450-r)(450+r)\left(\dfrac{2000}{450-r}+\dfrac{2000}{450+r}\right)=9(450-r)(450+r)\) Simplify. \(2000(450+r)+2000(450-r)=9(450-r)(450+r)\) Factor the \(2,000\). \(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\) Solve. \(2000(900)=9\left(450^{2}-r^{2}\right)\) Divide by \(9\). \(2000(100)=450^{2}-r^{2}\) Simplify. \(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\
The speed of the jet stream is \(50\) mph.
Check:
Is \(50\) mph a reasonable speed for the jet stream? Yes.
If the plane is traveling \(450\) mph and the wind is \(50\) mph,
Tailwind
\(450+50=500 \mathrm{mph} \quad \dfrac{2000}{500}=4\) hours
Headwind
\(450-50=400 \mathrm{mph} \quad \dfrac{2000}{400}=5\) hours
The times add to \(9\) hours, so it checks.
Answer the question. The speed of the jet stream was \(50\) mph.
MaryAnne just returned from a visit with her grandchildren back east. The trip was \(2400\) miles from her home and her total time in the airplane for the round trip was \(10\) hours. If the plane was flying at a rate of \(500\) miles per hour, what was the speed of the jet stream?
- Answer
-
The speed of the jet stream was \(100\) mph.
Gerry just returned from a cross country trip. The trip was \(3000\) miles from his home and his total time in the airplane for the round trip was \(11\) hours. If the plane was flying at a rate of \(550\) miles per hour, what was the speed of the jet stream?
- Answer
-
The speed of the jet stream was \(50\) mph.
Work applications can also be modeled by quadratic equations. We will set them up using the same methods we used when we solved them with rational equations.We’ll use a similar scenario now.
The weekly gossip magazine has a big story about the presidential election and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(12\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(8\) hours. How long does it take for each press to print the job alone?
- Solution
-
This is a work problem. A chart will help us organize the information.
We are looking for how many hours it would take each press separately to complete the job.
Let \(x=\) the number of hours for Press #2 to complete the job.
Enter the hours per job for Press #1, Press #2, and when they work together.
The part completed by Press #1 plus the part completed by Press #2 equals the amount completed together.
Translate to an equation.
Solve. 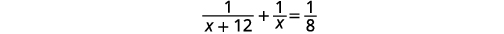
Multiply by the LCD, 8\(x(x+12)\). 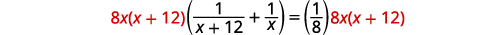
Simplify. 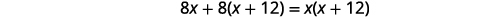
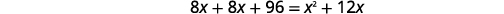
Figure 9.5.37 
Figure 9.5.38 Solve. 
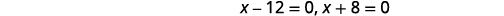
Figure 9.5.40 
Figure 9.5.41 Since the idea of negative hours does not make sense, we use the values \(x=12\). 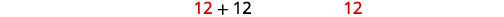
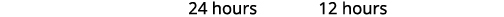
Figure 9.5.43 Write our sentence answer. Press #1 would take \(24\) hours and Press #2 would take \(12\) hours to do the job alone.
The weekly news magazine has a big story naming the Person of the Year and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(6\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(4\) hours. How long does it take for each press to print the job alone?
- Answer
-
Press #1 would take \(12\) hours, and Press #2 would take \(6\) hours to do the job alone.
Erlinda is having a party and wants to fill her hot tub. If she only uses the red hose it takes \(3\) hours more than if she only uses the green hose. If she uses both hoses together, the hot tub fills in \(2\) hours. How long does it take for each hose to fill the hot tub?
- Answer
-
The red hose take \(6\) hours and the green hose take \(3\) hours alone.
Key Concepts
- Methods to Solve Quadratic Equations
- Factoring
- Square Root Property
- Completing the Square
- Quadratic Formula
- How to use a Problem-Solving Strategy.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Area of a Triangle
- For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\dfrac{1}{2}bh\).
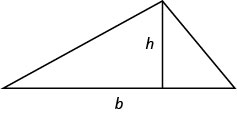
- Area of a Rectangle
- For a rectangle with length,\(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).
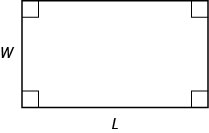
- Pythagorean Theorem
- In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, \(a^{2}+b^{2}=c^{2}\).
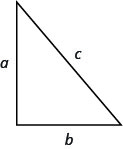
- Projectile motion
- The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula \(h=-16 t^{2}+v_{0} t\).
Practice Makes Perfect
In the following exercises, solve using any method.
- The product of two consecutive odd numbers is \(255\). Find the numbers.
- The product of two consecutive even numbers is \(360\). Find the numbers.
- The product of two consecutive even numbers is \(624\). Find the numbers.
- The product of two consecutive odd numbers is \(1,023\). Find the numbers.
- The product of two consecutive odd numbers is \(483\). Find the numbers.
- The product of two consecutive even numbers is \(528\). Find the numbers.
- Answer
-
1. Two consecutive odd numbers whose product is \(255\) are \(15\) and \(17\), and \(−15\) and \(−17\).
3. The first and second consecutive odd numbers are \(24\) and \(26\), and \(−26\) and \(−24\).
5. Two consecutive odd numbers whose product is \(483\) are \(21\) and \(23\), and \(−21\) and \(−23\).
In the following exercises, solve using any method. Round your answers to the nearest tenth, if needed.
- A triangle with area \(45\) square inches has a height that is two less than four times the base Find the base and height of the triangle.
- The base of a triangle is six more than twice the height. The area of the triangle is \(88\) square yards. Find the base and height of the triangle.
- The area of a triangular flower bed in the park has an area of \(120\) square feet. The base is \(4\) feet longer that twice the height. What are the base and height of the triangle?
- A triangular banner for the basketball championship hangs in the gym. It has an area of \(75\) square feet. What is the length of the base and height , if the base is two-thirds of the height?
- The length of a rectangular driveway is five feet more than three times the width. The area is \(50\) square feet. Find the length and width of the driveway.
- A rectangular lawn has area \(140\) square yards. Its length is six yards less than twice its width. What are the length and width of the lawn?
- A rectangular table for the dining room has a surface area of \(24\) square feet. The length is two more feet than twice the width of the table. Find the length and width of the table.
- The new computer has a surface area of \(168\) square inches. If the the width is \(5.5\) inches less that the length, what are the dimensions of the computer?
- The hypotenuse of a right triangle is twice the length of one of its legs. The length of the other leg is three feet. Find the lengths of the three sides of the triangle.
- The hypotenuse of a right triangle is \(10\) cm long. One of the triangle’s legs is three times as the length of the other leg . Round to the nearest tenth. Find the lengths of the three sides of the triangle.
- A rectangular garden will be divided into two plots by fencing it on the diagonal. The diagonal distance from one corner of the garden to the opposite corner is five yards longer than the width of the garden. The length of the garden is three times the width. Find the length of the diagonal of the garden.

18. Nautical flags are used to represent letters of the alphabet. The flag for the letter, O consists of a yellow right triangle and a red right triangle which are sewn together along their hypotenuse to form a square. The hypotenuse of the two triangles is three inches longer than a side of the flag. Find the length of the side of the flag.
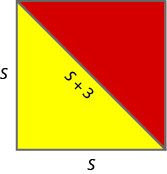
19. Gerry plans to place a \(25\)-foot ladder against the side of his house to clean his gutters. The bottom of the ladder will be \(5\) feet from the house.How for up the side of the house will the ladder reach?
20. John has a \(10\)-foot piece of rope that he wants to use to support his \(8\)-foot tree. How far from the base of the tree should he secure the rope?
21. An arrow is shot vertically upward at a rate of \(v_{0} = 220\) feet per second. Use the projectile formula \(h=-16 t^{2}+v_{0} t\), to determine when the height of the arrow will be \(400\) feet.
22. A firework rocket is shot upward at a rate of \(640\) ft/sec. Use the projectile formula \(h=-16 t^{2}+v_{0} t\) to determine when the height of the firework rocket will be \(1200\) feet.
23. A bullet is fired straight up from a BB gun with initial velocity \(1120\) feet per second at an initial height of \(8\) feet. Use the formula \(h=-16 t^{2}+v_{0} t+8\) to determine how many seconds it will take for the bullet to hit the ground. (That is, when will \(h=0\)?)
24. A stone is dropped from a \(196\)-foot platform. Use the formula \(h=-16 t^{2}+v_{0} t+196\) to determine how many seconds it will take for the stone to hit the ground. (Since the stone is dropped, \(v_{0}=0\).)
25. The businessman took a small airplane for a quick flight up the coast for a lunch meeting and then returned home. The plane flew a total of \(4\) hours and each way the trip was \(200\) miles. What was the speed of the wind that affected the plane which was flying at a speed of \(120\) mph?
26. The couple took a small airplane for a quick flight up to the wine country for a romantic dinner and then returned home. The plane flew a total of \(5\) hours and each way the trip was \(300\) miles. If the plane was flying at \(125\) mph, what was the speed of the wind that affected the plane?
27. Roy kayaked up the river and then back in a total time of \(6\) hours. The trip was \(4\) miles each way and the current was difficult. If Roy kayaked at a speed of \(5\) mph, what was the speed of the current?
28. Rick paddled up the river, spent the night camping, and then paddled back. He spent \(10\) hours paddling and the campground was \(24\) miles away. If Rick kayaked at a speed of \(5\) mph, what was the speed of the current?
29. Two painters can paint a room in \(2\) hours if they work together. The less experienced painter takes \(3\) hours more than the more experienced painter to finish the job. How long does it take for each painter to paint the room individually?
30. Two gardeners can do the weekly yard maintenance in \(8\) minutes if they work together. The older gardener takes \(12\) minutes more than the younger gardener to finish the job by himself. How long does it take for each gardener to do the weekly yard maintenance individually?
31. It takes two hours for two machines to manufacture \(10,000\) parts. If Machine #1 can do the job alone in one hour less than Machine #2 can do the job, how long does it take for each machine to manufacture \(10,000\) parts alone?
32. Sully is having a party and wants to fill his swimming pool. If he only uses his hose it takes \(2\) hours more than if he only uses his neighbor’s hose. If he uses both hoses together, the pool fills in \(4\) hours. How long does it take for each hose to fill the pool?
- Answer
-
7. The width of the triangle is \(5\) inches and the height is \(18\) inches.
9. The base is \(24\) feet and the height of the triangle is \(10\) feet.
11. The length of the driveway is \(15.0\) feet and the width is \(3.3\) feet.
13. The length of table is \(8\) feet and the width is \(3\) feet.
15. The length of the legs of the right triangle are \(3.2\) and \(9.6\) cm.
17. The length of the diagonal fencing is \(7.3\) yards.
19. The ladder will reach \(24.5\) feet on the side of the house.
21. The arrow will reach \(400\) feet on its way up in \(2.2\) seconds and on the way down in \(11.6\) seconds.
23. The bullet will take \(70\) seconds to hit the ground.
25. The speed of the wind was \(49\) mph.
27. The speed of the current was \(4.3\) mph.
29. The less experienced painter takes \(6\) hours and the experienced painter takes \(3\) hours to do the job alone.
31. Machine #1 takes \(3.6\) hours and Machine #2 takes \(4.6\) hours to do the job alone.
- Make up a problem involving the product of two consecutive odd integers.
- Start by choosing two consecutive odd integers. What are your integers?
- What is the product of your integers?
- Solve the equation \(n(n+2)=p\), where \(p\) is the product you found in part (b).
- Did you get the numbers you started with?
- Make up a problem involving the product of two consecutive even integers.
- Start by choosing two consecutive even integers. What are your integers?
- What is the product of your integers?
- Solve the equation \(n(n+2)=p\), where \(p\) is the product you found in part (b).
- Did you get the numbers you started with?
- Answer
-
33. Answers will vary.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


