8.1: More Parabolas

Last updated
Save as PDF

Page ID: 66397

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Graph vertical parabolas
Graph horizontal parabolas
Solve applications with parabolas

Before you get started, take this readiness quiz.

Graph: $y=-3 x^{2}+12 x-12$.
Solve by completing the square: $x^{2}-6 x+6=0$.
Write in standard form: $y=3 x^{2}-6 x+5$.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

This figure shows two cones placed point to point. They are labeled nappes.

There are four conics—the circle, parabola, ellipse, and hyperbola. The next figure shows how the plane intersecting the double cone results in each curve.

Each of these four figures shows a double cone intersected by a plane. In the first figure, the plane is perpendicular to the axis of the cones and intersects the bottom cone to form a circle. In the second figure, the plane is at an angle to the axis and intersects the bottom cone in such a way that it intersects the base as well. Thus, the curve formed by the intersection is open at both ends. This is labeled parabola. In the third figure, the plane is at an angle to the axis and intersects the bottom cone in such a way that it does not intersect the base of the cone. Thus, the curve formed by the intersection is a closed loop, labeled ellipse. In the fourth figure, the plane is parallel to the axis, intersecting both cones. This is labeled hyperbola.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a parabola

Graph Vertical Parabolas

The next conic section we will look at is a parabola.

Previously, we learned to graph vertical parabolas from the general form or the standard form using properties. Those methods will also work here. We will summarize the properties here.

Vertical Parabolas


	General form $y=a x^{2}+b x+c$	Standard Form $y=a(x-h)^{2}+k$
Orientation	$a>0$ up; $a<0$ down	$a>0$ up; $a<0$ down
Axis of Symmetry	$x=-\dfrac{b}{2 a}$	$x=h$
Vertex	Substitute $x=-\dfrac{b}{2 a}$ and solve for $y .$	$(h, k)$
$y$-intercept	Let $x=0$	Let $x=0$
$x$-intercepts	Let $y=0$	Let $y=0$

The graphs show what the parabolas look like when they open up or down. Their position in relation to the $x$- or $y$-axis is merely an example.

This figure shows two parabolas with axis x equals h and vertex h, k. The one on the left opens up and A is greater than 0. The one on the right opens down. Here A is less than 0.

To graph a parabola from these forms, we used the following steps.

Note

How to Graph Vertical Parabolas $y=a x^{2}+b x+c$ or $y=a(x-h)^{2}+k$ using Properties.

Step 1: Determine whether the parabola opens upward or downward.

Step 2. Find the axis of symmetry.

Step 3. Find the vertex.

Step 4. Find the $y$-intercept. Find the point symmetric to the $y$-intercept across the axis of symmetry.

Step 5. Find the $x$-intercepts.

Step 6. Graph the parabola.

The next example reviews the method of graphing a parabola from the general form of its equation.

Example $\PageIndex{1}$

Graph $y=-x^{2}+6 x-8$ by using properties.

Solution:


	$\stackrel{y=-x^{2}+6 x-8}{y=ax^2+bx+c}$
Since $a$ is $-1$, the parabola opens downward.
$.$
To find the axis of symmetry, find $x=-\dfrac{b}{2 a}$.	$x=-\dfrac{b}{2a}$
	$x=-\dfrac{6}{2(-1)}$ $x=3$
Identify the axis of symmetry	The axis of symmetry is $x=3$.
	$.$
Find the vertex. Note the vertex is on the line $x=3$.
Let $x=3$ and find $y$ so that $(3,y)$ is on the graph, i.e., is a solution to the equation.	$y=-x^{2}+6 x-8$ $y=-(3)^2+6(3)-8$ $y=-9+18-8$ $y=1$
	The vertex is $(3,1)$.
	$.$
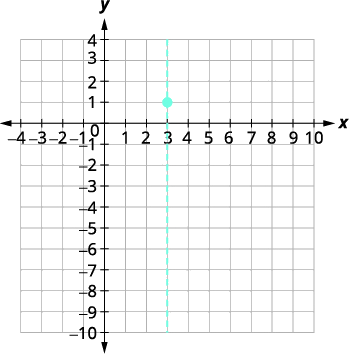The $y$-intercept occurs when $x=0$. Substitute $x=0$.	$y=-x^{2}+6 x-8$ $y=-(0)^2+6(0)-8$ $y=-8$
	The $y$-intercept is $(0,-8)$.
The point $(0,−8)$ is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is $(6,−8)$.	Point symmetric to the $y$-intercept is $(6,−8)$.
	$.$
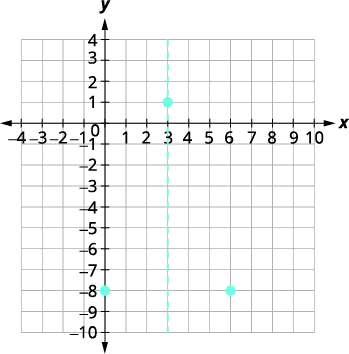The $x$-intercept occurs when $y=0$. Let $y=0$.	$0=-x^2+6x-8$
Factor the GCF.	$0=-(x^2-6x+8)$
Factor the trinomial.	$0=-(x-4)(x-2)$
Solve for $x$.	$x-4=0$ or $x-2=0$ $x=4$ or $x=2$
	The $x$-intercepts are $(4,0),(2,0)$.
Graph the parabola.	$.$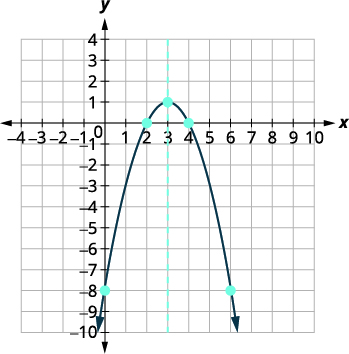

Try It $\PageIndex{2}$

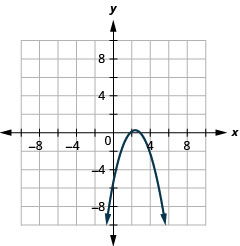
Graph $y=-x^{2}+5 x-6$ by using properties.

Answer: $This graph shows a parabola opening downward, with x intercepts (2, 0) and (3, 0) and y intercept (0, negative 6).$

Try It $\PageIndex{3}$

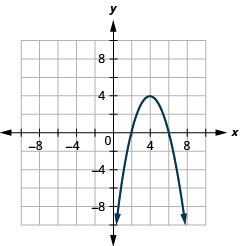
Graph $y=-x^{2}+8 x-12$ by using properties.

Answer: $This graph shows a parabola opening downward, with vertex (4, 4) and x intercepts (2, 0) and (6, 0).$

The next example reviews the method of graphing a parabola from the standard form of its equation, $y=a(x-h)^{2}+k$.

Example $\PageIndex{4}$

Write $y=3 x^{2}-6 x+5$ in standard form and then use properties of standard form to graph the equation.

Solution:


Rewrite the equation in $y=a(x-h)^{2}+k$ form by completing the square.


	$y=3(x-1)^{2}+2$
Identify the constants $a, h, k$.	$a=3, h=1, k=2$
Since $a=2$, the parabola opens upward.
$.$
The axis of symmetry is $x=h$.	The axis of symmetry is $x=1$.
The vertex is $(h,k)$.	The vertex is $(1,2)$.
Find the $y$-intercept by substituting $x=0$,	$y=3(x-1)^{2}+2$ $y=3 \cdot 0^{2}-6 \cdot 0+5$
	$y=5$
	$y$-intercept $(0,5)$
Find the point symmetric to $(0,5)$ across the axis of symmetry.	$(2,5)$
Find the $x$-intercepts.
	The square root of a negative number tells us the solutions are complex numbers. So there are no $x$-intercepts.
Graph the parabola.	$.$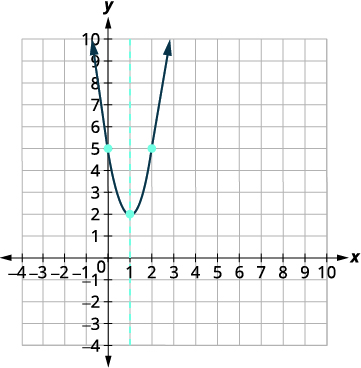

Try It $\PageIndex{5}$

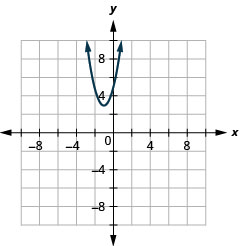
Write $y=2 x^{2}+4 x+5$ in standard form and
use properties of standard form to graph the equation.

Answer

$y=2(x+1)^{2}+3$

This graph shows a parabola opening upwards, with vertex (negative 1, 3) and y intercept (0, 5). It has the point minus (2, 5) on it.

Try It $\PageIndex{6}$

Write $y=-2 x^{2}+8 x-7$ in standard form and
use properties of standard form to graph the equation.

Answer

$y=-2(x-2)^{2}+1$

This graph shows a parabola opening downwards, with vertex (2, 1) and axis of symmetry x equals 2. Its y intercept is (0, negative 7).

Graph Horizontal Parabolas

Our work so far has only dealt with parabolas that open up or down. We are now going to look at horizontal parabolas. These parabolas open either to the left or to the right. If we interchange the $x$ and $y$ in our previous equations for parabolas, we get the equations for the parabolas that open to the left or to the right.

Horizontal Parabolas


	General form $x=a y^{2}+b y+c$	Standard form $x=a(y-k)^{2}+h$
Orientation	$a>0$ right; $a<0$ left	$a>0$ right; $a<0$ left
Axis of Symmetry	$y=-\dfrac{b}{2 a}$	$y=k$
Vertex	Substitute $y=-\dfrac{b}{2 a}$ and solve for $x .$	$(h, k)$
$x$-intercepts	Let $x=0$	Let $x=0$
$y$-intercept	Let $y=0$	Let $y=0$

The graphs show what the parabolas look like when they to the left or to the right. Their position in relation to the $x$- or $y$-axis is merely an example.

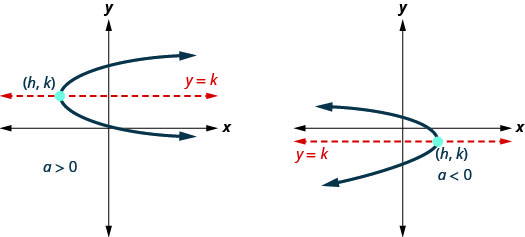
This figure shows two parabolas with axis of symmetry y equals k,) and vertex (h, k. The one on the left is labeled a greater than 0 and opens to the right. The other parabola opens to the left. — Figure 11.2.30

To graph a parabola that opens to the left or to the right is basically the same as what we did for parabolas that open up or down, with the reversal of the $x$ and $y$ variables. The graph is then the one we would get by graphing the equation with the $x$ and $y$ exchanged, and exchanging the $x$ and $y$ coordinates (e.g., if (2,3) is on the graph of the equation with the exchange, then (3,2) is on the graph of the given equation).

Graph Horizontal Parabolas $x=a y^{2}+b y+c$ or $x=a(y-h)^{2}+k$ using Properties

Step 1: Determine whether the parabola opens to the left or to the right.
Step 2: Find the axis of symmetry.
Step 3: Find the vertex.
Step 4: Find the $x$-intercept. Find the point symmetric to the $x$-intercept across the axis of symmetry.
Step 5: Find the $y$-intercepts.
Step 6: Graph the parabola.

Example $\PageIndex{7}$

Graph $x=2 y^{2}$ by using properties.

Solution:

	$\stackrel{x=2y^2}{x=ay^2+by+c}$
Since $a=2$, the parabola opens to the right.
$.$
To find the axis of symmetry, find $y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2a}$ $y=-\dfrac{0}{2(2)}$ $y=0$ The axis of symmetry is $y=0$.
The vertex is on the line $y=0$. Let $y=0$.	$x=2y^2$ $x=2\cdot(0)^2$ $x=0$ The vertex is $(0,0)$.

Since the vertex is $(0,0)$, both the $x$- and $y$-intercepts are the point $(0,0)$. To graph the parabola we need more points. In this case it is easiest to choose values of $y$.

$y$	$x$	$(x,y)$
$1$	$x=2\cdot 1^2=2$	$(1,2)$
$2$	$x=2\cdot (2)^2=2\cdot 4=8$	$(8,2)$

We also plot the points symmetric to $(2,1)$ and $(8,2)$ across the $y$-axis, the points $(2,−1),(8,−2)$.

Graph the parabola.

This graph shows right opening parabola with vertex (0, 0). Four points are marked on it: point (2, 1), point (2, negative 1), point (8, 2) and point (8 minus 2).

Try It $\PageIndex{8}$

Graph $x=y^{2}$ by using properties.

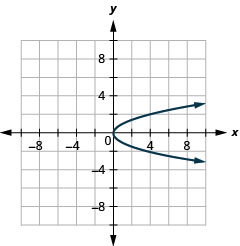
Answer: $This graph shows right opening parabola with vertex at origin. Two points on it are (4, 2) and (4, negative 2).$
Figure 11.2.40

Try It $\PageIndex{9}$

Graph $x=-y^{2}$ by using properties.

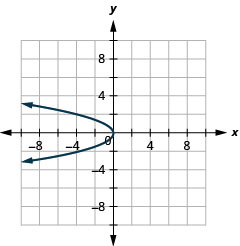
Answer: $This graph shows left opening parabola with vertex at origin. Two points on it are (negative 4, 2) and (negative 4, negative 2).$
Figure 11.2.41

In the next example, the vertex is not the origin.

Example $\PageIndex{10}$

Graph $x=-y^{2}+2 y+8$ by using properties.

Solution:

$\stackrel{x=-y^{2}+2 y+8}{x=ay^2+by+c}$

Since $a=-1$, the parabola opens to the left.

$.$

To find the axis of symmetry,
find $y=-\dfrac{b}{2 a}$

$y=-\dfrac{b}{2a}$

$y=-\dfrac{2}{2(-1)}$

$y=1$

The axis of symmetry is $y=1$.

The vertex is on the line $y=1$.

Let $y=1$.

$x=-y^{2}+2 y+8$

$x=-(1)^2+2(1)+8$

$x=9$

The vertex is $(9,1)$.

The $x$-intercept occurs when $y=0$.

$x=-y^{2}+2 y+8$

$x=-(0)^2+2(0)+8$

$x=8$

The $x$-intercept is $(8,0)$.

The point $(8,0)$ is one unit below the line of
symmetry. The symmetric point one unit
above the line of symmetry is $(8,2)$

Symmetric point is $(8,2)$.

The $y$-intercept occurs when $x=0$.

Substitute $x=0$.

$x=-y^{2}+2 y+8$

$0=-y^{2}+2 y+8$

Solve.

$y^2-2y-8=0$

$(y-4)(y+2)=0$

$y-4=0$ or $y+2=0$

$y=4$ or $y=-2$

The $y$ -intercepts are $(0,4)$ and $(0,-2)$.

Connect the points to graph the parabola.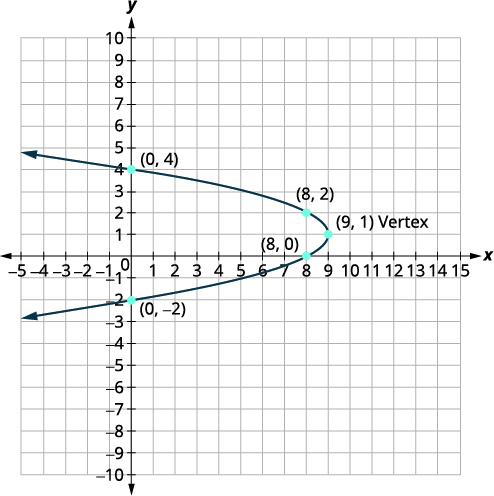

$.$

Table 11.2.6

Try It $\PageIndex{11}$

Graph $x=-y^{2}-4 y+12$ by using properties.

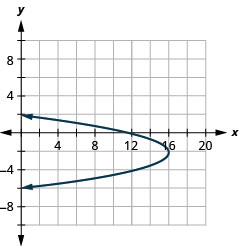
Answer: $This graph shows left opening parabola with vertex (16, negative 2) and x intercept (12, 0).$
Figure 11.2.58

Try It $\PageIndex{12}$

Graph $x=-y^{2}+2 y-3$ by using properties.

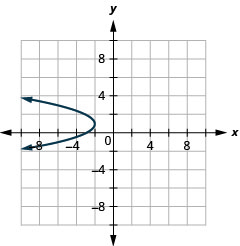
Answer: $This graph shows left opening parabola with vertex (negative 2, 1) and x intercept minus (3, 0).$
Figure 11.2.59

We will use the properties of the parabola in the next example.

Example $\PageIndex{13}$

Graph $x=2(y-2)^{2}+1$ using properties.

Solution:

Table 11.2.7
	$\stackrel{x=2(y-2)^{2}+1}{x=a(y-k)^2+h}$
Identify the constants $a, h, k$.	$a=2, h=1, k=2$
Since $a=2$, the parabola opens to the right.
$.$
The axis of symmetry is $y=k$.	The axis of symmetry is $y=2$.
The vertex is $(h,k)$.	The vertex is $(1,2)$.
Find the $x$-intercept by substituting $y=0$.	$x=2(y-2)^{2}+1$ $x=2(0-2)^{2}+1$ $x=9$
	The $x$-intercept is $(9,0)$.
Find the point symmetric to $(9,0)$ across the axis of symmetry.	$(9,4)$
Find the $y$-intercepts. Let $x=0$.
	A square cannot be negative, so there is no real solution. So there are no $y$-intercepts.
Graph the parabola.	$.$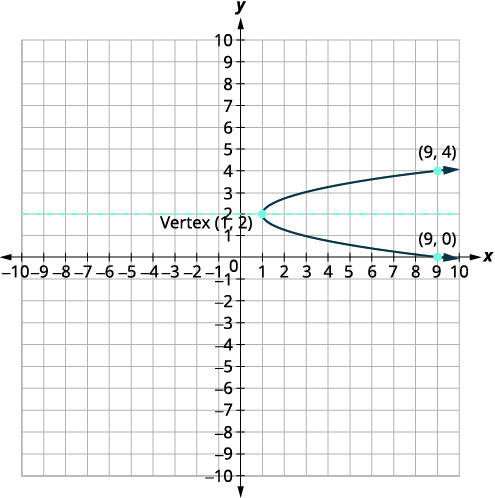

Try It $\PageIndex{14}$

Graph $x=3(y-1)^{2}+2$ using properties.

Answer: $This graph shows a parabola opening right with vertex (2, 1) and x intercept (5, 0).$

Try It $\PageIndex{15}$

Graph $x=2(y-3)^{2}+2$ using properties.

Answer: $This graph shows a parabola opening right with vertex (2, 3) and symmetric points (4, 2) and (4, 4).$

In the next example, we notice the a is negative and so the parabola opens to the left.

Example $\PageIndex{16}$

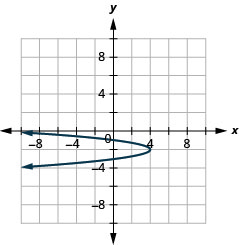
Graph $x=-4(y+1)^{2}+4$ using properties.

Solution:


	$\stackrel{x=-4(y+1)^{2}+4}{x=a(y-k)^2+h}$
Identify the constants $a, h, k$.	$a=-4, h=4, k=-1$
Since $a=-4$, the parabola opens to the left.
$.$
The axis of symmetry is $y=k$.	The axis of symmetry is $y=-1$.
The vertex is $(h,k)$.	The vertex is $(4,-1)$.
Find the $x$-intercept by substituting $y=0$.	$x=-4(y+1)^{2}+4$ $x=-4(0+1)^{2}+4$ $x=0$
	The $x$-intercept is $(0,0)$.
Find the point symmetric to $(0,0)$ across the axis of symmetry.	$(0,-2)$
Find the $y$-intercepts.	$x=-4(y+1)^{2}+4$
Let $x=0$.
	$y=-1+1 \quad y=-1-1$
	$y=0 \quad\quad y=-2$
	The $y$-intercepts are $(0,0)$ and $(0,-2)$.
Graph the parabola.	$.$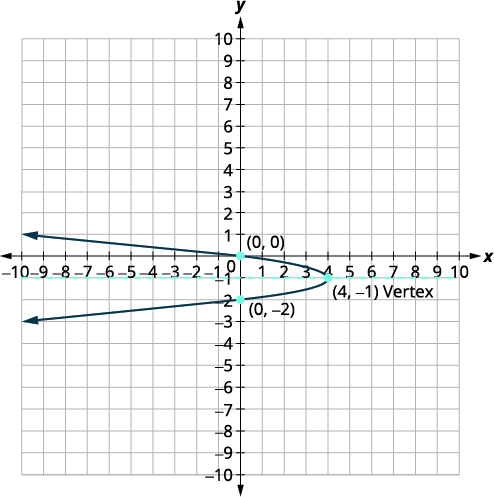

Try It $\PageIndex{17}$

Graph $x=-4(y+2)^{2}+4$ using properties.

Answer: $This figure shows a parabola opening to the left with vertex (4, negative 2) and y intercepts (0, negative 1) and (0, negative 3).$

Try It $\PageIndex{18}$

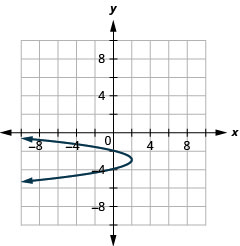
Graph $x=-2(y+3)^{2}+2$ using properties.

Answer: $This figure shows a parabola opening to the left with vertex (2, negative 3) and y intercepts (0, negative 2) and (0, negative 4).$

The next example requires that we first put the equation in standard form and then use the properties.

Example $\PageIndex{19}$

Write $x=2 y^{2}+12 y+17$ in standard form and then use the properties of the standard form to graph the equation.

Solution:

$x=2y^2+12y+17$

Rewrite the equation in $x=a(y-k)^{2}+h$ form by completing the square.

$x=2(y^2+6y)+17$

$x=2((y^2+6y+9)-9)+17$

$x=2(y^2+6y+9)-18+17$

$x=2(y+3)^2-1$

Identify the constants $a, h, k$.

$\stackrel{x=2(y+3)^{2}-1}{x=a(y-k)^2+h}$

$a=2, h=-1, k=-3$

Since $a=2$, the parabola opens to the right.

$.$

The axis of symmetry is $y=k$.

The axis of symmetry is $y=-3$.

The vertex is $(h,k)$.

The vertex is $(-1,-3)$.

Find the $x$-intercept by substituting $y=0$.

$x=2(y+3)^{2}-1$
$x=2(0+3)^{2}-1$
$x=17$

The $x$-intercept is $(17,0)$.

Find the point symmetric to $(17,0)$ across the axis of symmetry.

$(17,-6)$

Find the $y$-intercepts.

Let $x=0$.

$0=2(y+3)^2-1$

$(y+3)^2=\dfrac12$

$y+3=\pm\dfrac{1}{\sqrt{2}}=\pm\dfrac{\sqrt{2}}{2}$

$y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}$

The $y$-intercepts are $\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)$.

Approximate so that the points can be located on the graph.

The $y$ intercepts are approximately $(0,-2.3)$ and $(0,-3.7)$

Graph the parabola.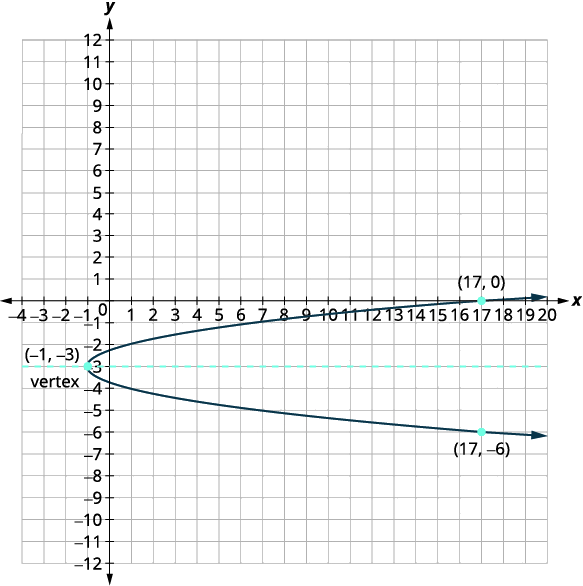

$.$

Try It $\PageIndex{20}$

Write $x=3 y^{2}+6 y+7$ in standard form and
Use properties of the standard form to graph the equation.

Answer

$x=3(y+1)^{2}+4$

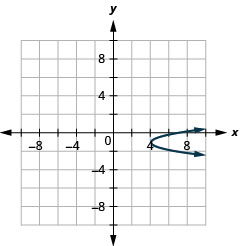
This graph shows a parabola opening to the right with vertex (4, negative 1) and x intercept (7, 0).

Try It $\PageIndex{21}$

Write $x=-4 y^{2}-16 y-12$ in standard form and
Use properties of the standard form to graph the equation.

Answer

$x=-4(y+2)^{2}+4$

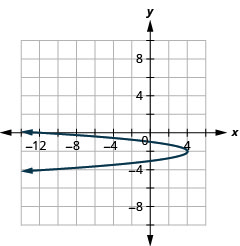
This graph shows a parabola opening to the left with vertex (4, negative 2) and x intercept minus (12, 0).

Another Look at Parabolas

We have learned here how to graph both vertical and horizontal parabolas. We started with the basic graphs of $y=x^2$ and $x=y^2$. We then were able to graph $y=(x-h)^2+k$ and $x=(y-k)^2+h$. If we subtract the $k$ on both sides of the first equation and $h$ on both sides of the second, we have equivalent equations (they have the same solutions) $y-k=(x-h)^2$ and $x-h=(y-k)^2$. The vertex of the parabolas are the 'simplest' solution that results in $0=0$ when being substituted, namely, $(h,k)$. So, the parabolas can be graphed by translating the basic form so that the vertex sits at $(h,k)$. Viewing parabolas in this way will lead more naturally into the next section.

Solve Applications with Parabolas

Many architectural designs incorporate parabolas. It is not uncommon for bridges to be constructed using parabolas as we will see in the next example.

Example $\PageIndex{22}$

Find the equation of the parabolic arch formed in the foundation of the bridge shown. Write the equation in standard form.

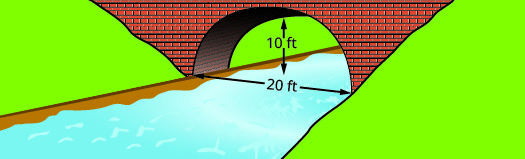
This figure shows a parabolic arch formed in the foundation of a bridge. It is 10 feet high and 20 feet wide at the base.

Solution:

We will first set up a coordinate system and draw the parabola. The graph will give us the information we need to write the equation of the graph in the standard form $y=a(x-h)^{2}+k$.


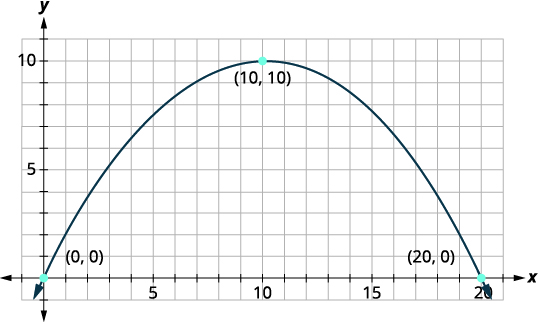Let the lower left side of the bridge be the origin of the coordinate grid at the point $(0,0)$. Since the base is $20$ feet wide the point $(20,0)$ represents the lower right side. The bridge is 10 feet high at the highest point. The highest point is the vertex of the parabola so the $y$-coordinate of the vertex will be $10$. Since the bridge is symmetric, the vertex must fall halfway between the left most point, $(0,0)$, and the rightmost point $(20,0)$. From this we know that the $x$-coordinate of the vertex will also be $10$.	$.$
Identify the vertex, $(h,k)$.	$(h, k)=(10,10)$
	$h=10, \quad k=10$
Substitute the values into the standard form. The value of $a$ is still unknown. To find the value of $a$ use one of the other points on the parabola.	$\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}$
Substitute the values of the other point into the equation.	$y=a(x-10)^{2}+10$ $0=a(0-10)^{2}+10$
Solve for $a$.
	$y=a(x-10)^{2}+10$
Substitute the value for $a$ into the equation.	$y=-\dfrac{1}{10}(x-10)^{2}+10$

Try It $\PageIndex{23}$

Find the equation of the parabolic arch formed in the foundation of the bridge shown. Write the equation in standard form.

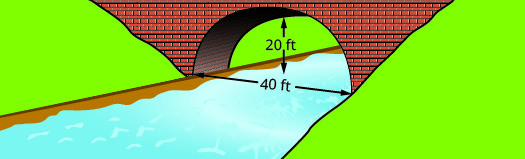
This figure shows a parabolic arch formed in the foundation of a bridge. It is 20 feet high and 40 feet wide at the base.

Answer: $y=-\dfrac{1}{20}(x-20)^{2}+20$

Try It $\PageIndex{24}$

Find the equation of the parabolic arch formed in the foundation of the bridge shown. Write the equation in standard form.

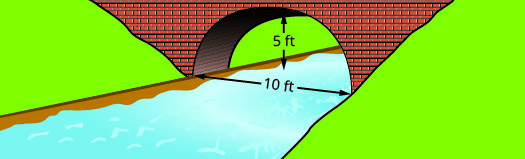
This figure shows a parabolic arch formed in the foundation of a bridge. It is 5 feet high and 10 feet wide at the base.

Answer: $y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5$

Key Concepts

Parabola: Parabolas are examples of conic sections. The graphs of the equations of the form $y=ax^2+bx+c$ and $x=ay^2+by+c$ are examples of what are called parabolas.

Vertical Parabolas

Table 11.2.1
	General form $y=a x^{2}+b x+c$	Standard Form $y=a(x-h)^{2}+k$
Orientation	$a>0$ up; $a<0$ down	$a>0$ up; $a<0$ down
Axis of Symmetry	$x=-\dfrac{b}{2 a}$	$x=h$
Vertex	Substitute $x=-\dfrac{b}{2 a}$ and solve for $y .$	$(h, k)$
$y$-intercept	Let $x=0$	Let $x=0$
$x$-intercepts	Let $y=0$	Let $y=0$

How to graph vertical parabolas $y=a x^{2}+b x+c$ or $y=a(x-h)^{2}+k$ using properties.

Determine whether the parabola opens upward or downward.
Find the axis of symmetry.
Find the vertex.
Find the $y$-intercept. Find the point symmetric to the $y$-intercept across the axis of symmetry.
Find the $x$-intercepts.
Graph the parabola.

Horizontal Parabolas

Table 11.2.4
	General form $x=a y^{2}+b y+c$	Standard form $x=a(y-k)^{2}+h$
Orientation	$a>0$ right; $a<0$ left	$a>0$ right; $a<0$ left
Axis of Symmetry	$y=-\dfrac{b}{2 a}$	$y=k$
Vertex	Substitute $y=-\dfrac{b}{2 a}$ and solve for $x .$	$(h, k)$
$x$-intercepts	Let $x=0$	Let $x=0$
$y$-intercept	Let $y=0$	Let $y=0$

How to graph horizontal parabolas $x=a y^{2}+b y+c$ or $x=a(y-k)^{2}+h$ using properties.

Determine whether the parabola opens to the left or to the right.
Find the axis of symmetry.
Find the vertex.
Find the $x$-intercept. Find the point symmetric to the $x$-intercept across the axis of symmetry.
Find the $y$-intercepts.
Graph the parabola.

Glossary

parabola: A parabola is one of the conic sections. Though we do not discuss this here, it can be geometrically described: all points in a plane that are the same distance from a fixed point and a fixed line. The graphs of equations of the form $y=ax^2+bx+c$ and $x=ay^2+by+c$, $a\not= 0$ are examples of parabolas.

Practice Makes Perfect

Graph Vertical Parabolas

In the following exercises, graph each equation by using properties.

$y=-x^{2}+4 x-3$
$y=-x^{2}+8 x-15$
$y=6 x^{2}+2 x-1$
$y=8 x^{2}-10 x+3$

Answer

This graph shows a parabola opening downward with vertex (2, 1) and x intercepts (1, 0) and (3, 0). — Figure 11.2.83

This graph shows a parabola opening upward. The vertex is (negative 0.167, negative 1.167), the x intercepts are (negative 0.608) and (negative 0.274, 0), and the y-intercept is (0, negative 1). — Figure 11.2.84

Graph Vertical Parabolas

In the following exercises,

Write the equation in standard form and
Use properties of the standard form to graph the equation.

$y=-x^{2}+2 x-4$
$y=2 x^{2}+4 x+6$
$y=-2 x^{2}-4 x-5$
$y=3 x^{2}-12 x+7$

Answer

$y=-(x-1)^{2}-3$

This graph shows a parabola opening downward with vertex (1, negative 3) and y intercept (0, 4). — Figure 11.2.85

$y=-2(x+1)^{2}-3$

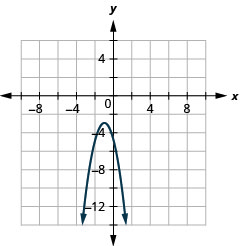
This graph shows a parabola opening downward with vertex (negative 1, negative 3) and x intercepts (negative 5, 0). — Figure 11.2.86

Graph Horizontal Parabolas

In the following exercises, graph each equation by using properties.

$x=-2 y^{2}$
$x=3 y^{2}$
$x=4 y^{2}$
$x=-4 y^{2}$
$x=-y^{2}-2 y+3$
$x=-y^{2}-4 y+5$
$x=y^{2}+6 y+8$
$x=y^{2}-4 y-12$
$x=(y-2)^{2}+3$
$x=(y-1)^{2}+4$
$x=-(y-1)^{2}+2$
$x=-(y-4)^{2}+3$
$x=(y+2)^{2}+1$
$x=(y+1)^{2}+2$
$x=-(y+3)^{2}+2$
$x=-(y+4)^{2}+3$
$x=-3(y-2)^{2}+3$
$x=-2(y-1)^{2}+2$
$x=4(y+1)^{2}-4$
$x=2(y+4)^{2}-2$

Answer

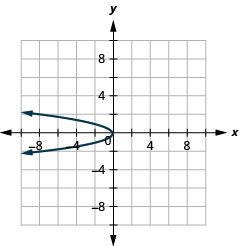
This graph shows a parabola opening to the left with vertex (0, 0). Two points on it are (negative 2, 1) and (negative 2, negative 1). — Figure 11.2.87

11.

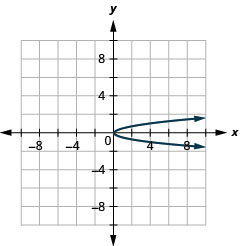
This graph shows a parabola opening to the right with vertex (0, 0). Two points on it are (4, 1) and (4, negative 1). — Figure 11.2.88

13.

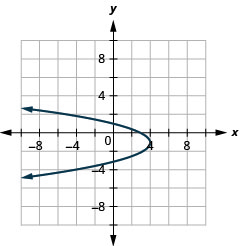
This graph shows a parabola opening to the left with vertex (4, negative 1) and y intercepts (0, 1) and (0, negative 3). — Figure 11.2.89

15.

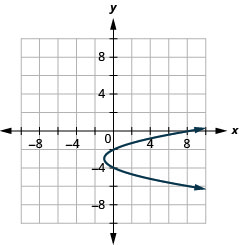
This graph shows a parabola opening to the right with vertex (negative 1, negative 3) and y intercepts (0, negative 2) and (0, negative 4). — Figure 11.2.90

17.

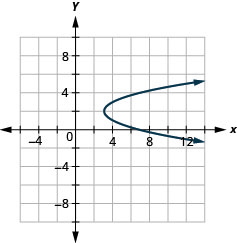
This graph shows a parabola opening to the right with vertex (3, 2) and x intercept (7, 0). — Figure 11.2.91

19.

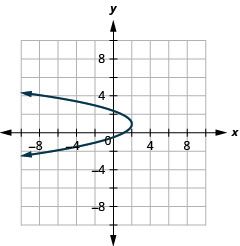
This graph shows a parabola opening to the left with vertex (2, 1) and x intercept (1, 0). — Figure 11.2.92

21.

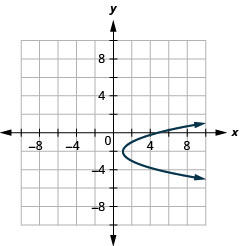
This graph shows a parabola opening to the right with vertex (1, negative 2) and x intercept (5, 0). — Figure 11.2.93

23.

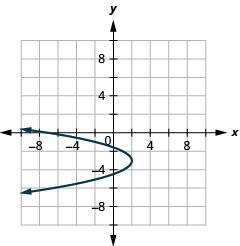
This graph shows a parabola opening to the left with vertex (2, negative 3). Two points on it are (negative 2, negative 1) and (negative 2, 5). — Figure 11.2.94

25.

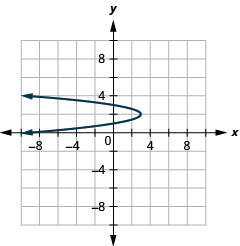
This graph shows a parabola opening to the left with vertex (3, 2) and y intercepts (0, 1) and (0, 3). — Figure 11.2.95

27.

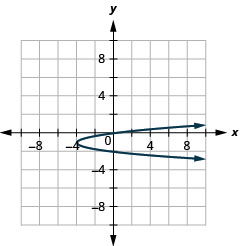
This graph shows a parabola opening to the right with vertex (negative 4, negative 1) and y intercepts (0, 0) and (0, negative 2). — Figure 11.2.96

Graph Horizontal Parabolas

In the following exercises,

Write the equation in standard form and
Use properties of the standard form to graph the equation.

$x=y^{2}+4 y-5$
$x=y^{2}+2 y-3$
$x=-2 y^{2}-12 y-16$
$x=-3 y^{2}-6 y-5$

Answer

29.

$x=(y+2)^{2}-9$

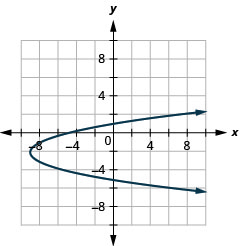
This graph shows a parabola opening to the right with vertex (negative 9, negative 2) and y intercepts (0, 1) and (0, negative 5). — Figure 11.2.97

31.

$x=-2(y+3)^{2}+2$

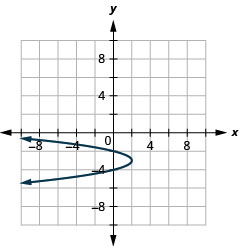
This graph shows a parabola opening to the left with vertex (2, negative 3) and y intercepts (0, negative 2) and (0, negative 4). — Figure 11.2.98

Solve Applications with Parabolas

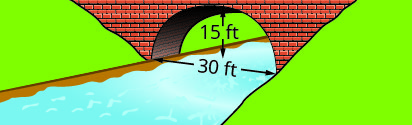
Write the equation in standard form of the parabolic arch formed in the foundation of the bridge shown. Use the lower left side of the bridge as the origin $(0, 0)$.

33.

This graph shows circle with center (negative 5, negative 2) and radius 2 units. — Figure 11.2.105

34.

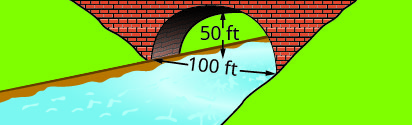
This figure shows a parabolic arch formed in the foundation of a bridge. It is 50 feet high and 100 feet wide at the base. — Figure 11.2.106

35.

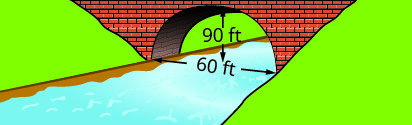
This figure shows a parabolic arch formed in the foundation of a bridge. It is 90 feet high and 60 feet wide at the base. — Figure 11.2.107

36.

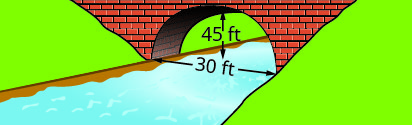
This figure shows a parabolic arch formed in the foundation of a bridge. It is 45 feet high and 30 feet wide at the base. — Figure 11.2.108

Answer

33. $y=-\dfrac{1}{15}(x-15)^{2}+15$

35. $y=-\dfrac{1}{10}(x-30)^{2}+90$

Writing Exercises

In your own words, define a parabola.
Is the parabola $y=x^{2}$ a function? Is the parabola $x=y^{2}$ a function? Explain why or why not.
Write the equation of a parabola that opens up or down in standard form and the equation of a parabola that opens left or right in standard form. Provide a sketch of the parabola for each one, label the vertex and axis of symmetry.
Explain in your own words, how you can tell from its equation whether a parabola opens up, down, left or right.

Answer

37. Answers may vary

39. Answers may vary

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

This table has four columns, 3 rows and a header row. The header row labels each column I can, confidently, with some help and no, I donâ€™t get it. The first column has the following statements: graph vertical parabolas, graph horizontal parabolas, solve applications with parabolas. The remaining columns are blank.

b. After reviewing this checklist, what will you do to become confident for all objectives?

	General form \(y=a x^{2}+b x+c\)	Standard Form \(y=a(x-h)^{2}+k\)
Orientation	\(a>0\) up; \(a<0\) down	\(a>0\) up; \(a<0\) down
Axis of Symmetry	\(x=-\dfrac{b}{2 a}\)	\(x=h\)
Vertex	Substitute \(x=-\dfrac{b}{2 a}\) and solve for \(y .\)	\((h, k)\)
\(y\)-intercept	Let \(x=0\)	Let \(x=0\)
\(x\)-intercepts	Let \(y=0\)	Let \(y=0\)

	\(\stackrel{y=-x^{2}+6 x-8}{y=ax^2+bx+c}\)
Since \(a\) is \(-1\), the parabola opens downward.
$.$
To find the axis of symmetry, find \(x=-\dfrac{b}{2 a}\).	\(x=-\dfrac{b}{2a}\)
	\(x=-\dfrac{6}{2(-1)}\) \(x=3\)
Identify the axis of symmetry	The axis of symmetry is \(x=3\).
	$.$
Find the vertex. Note the vertex is on the line \(x=3\).
Let \(x=3\) and find \(y\) so that \((3,y)\) is on the graph, i.e., is a solution to the equation.	\(y=-x^{2}+6 x-8\) \(y=-(3)^2+6(3)-8\) \(y=-9+18-8\) \(y=1\)
	The vertex is \((3,1)\).
	$.$
The \(y\)-intercept occurs when \(x=0\). Substitute \(x=0\).	\(y=-x^{2}+6 x-8\) \(y=-(0)^2+6(0)-8\) \(y=-8\)
	The \(y\)-intercept is \((0,-8)\).
The point \((0,−8)\) is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is \((6,−8)\).	Point symmetric to the \(y\)-intercept is \((6,−8)\).
	$.$
The \(x\)-intercept occurs when \(y=0\). Let \(y=0\).	\(0=-x^2+6x-8\)
Factor the GCF.	\(0=-(x^2-6x+8)\)
Factor the trinomial.	\(0=-(x-4)(x-2)\)
Solve for \(x\).	\(x-4=0\) or \(x-2=0\) \(x=4\) or \(x=2\)
	The \(x\)-intercepts are \((4,0),(2,0)\).
Graph the parabola.	$.$

Rewrite the equation in \(y=a(x-h)^{2}+k\) form by completing the square.


	\(y=3(x-1)^{2}+2\)
Identify the constants \(a, h, k\).	\(a=3, h=1, k=2\)
Since \(a=2\), the parabola opens upward.
$.$
The axis of symmetry is \(x=h\).	The axis of symmetry is \(x=1\).
The vertex is \((h,k)\).	The vertex is \((1,2)\).
Find the \(y\)-intercept by substituting \(x=0\),	\(y=3(x-1)^{2}+2\) \(y=3 \cdot 0^{2}-6 \cdot 0+5\)
	\(y=5\)
	\(y\)-intercept \((0,5)\)
Find the point symmetric to \((0,5)\) across the axis of symmetry.	\((2,5)\)
Find the \(x\)-intercepts.
	The square root of a negative number tells us the solutions are complex numbers. So there are no \(x\)-intercepts.
Graph the parabola.	$.$

	General form \(x=a y^{2}+b y+c\)	Standard form \(x=a(y-k)^{2}+h\)
Orientation	\(a>0\) right; \(a<0\) left	\(a>0\) right; \(a<0\) left
Axis of Symmetry	\(y=-\dfrac{b}{2 a}\)	\(y=k\)
Vertex	Substitute \(y=-\dfrac{b}{2 a}\) and solve for \(x .\)	\((h, k)\)
\(x\)-intercepts	Let \(x=0\)	Let \(x=0\)
\(y\)-intercept	Let \(y=0\)	Let \(y=0\)

	\(\stackrel{x=2y^2}{x=ay^2+by+c}\)
Since \(a=2\), the parabola opens to the right.
$.$
To find the axis of symmetry, find \(y=-\dfrac{b}{2 a}\)	\(y=-\dfrac{b}{2a}\) \(y=-\dfrac{0}{2(2)}\) \(y=0\) The axis of symmetry is \(y=0\).
The vertex is on the line \(y=0\). Let \(y=0\).	\(x=2y^2\) \(x=2\cdot(0)^2\) \(x=0\) The vertex is \((0,0)\).

Search

Note

Example \(\PageIndex{1}\)

Try It \(\PageIndex{2}\)

Try It \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Graph Horizontal Parabolas \(x=a y^{2}+b y+c\) or \(x=a(y-h)^{2}+k\) using Properties

Example \(\PageIndex{7}\)

Try It \(\PageIndex{8}\)

Try It \(\PageIndex{9}\)

Example \(\PageIndex{10}\)

Try It \(\PageIndex{11}\)

Try It \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Try It \(\PageIndex{14}\)

Try It \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Try It \(\PageIndex{17}\)

Try It \(\PageIndex{18}\)

Example \(\PageIndex{19}\)

Try It \(\PageIndex{20}\)

Try It \(\PageIndex{21}\)

Example \(\PageIndex{22}\)

Try It \(\PageIndex{23}\)

Try It \(\PageIndex{24}\)

Graph Vertical Parabolas

Graph Vertical Parabolas

Graph Horizontal Parabolas

Graph Horizontal Parabolas

Solve Applications with Parabolas

Writing Exercises

\(y\)	\(x\)	\((x,y)\)
\(1\)	\(x=2\cdot 1^2=2\)	\((1,2)\)
\(2\)	\(x=2\cdot (2)^2=2\cdot 4=8\)	\((8,2)\)

	\(\stackrel{x=2(y-2)^{2}+1}{x=a(y-k)^2+h}\)
Identify the constants \(a, h, k\).	\(a=2, h=1, k=2\)
Since \(a=2\), the parabola opens to the right.
$.$
The axis of symmetry is \(y=k\).	The axis of symmetry is \(y=2\).
The vertex is \((h,k)\).	The vertex is \((1,2)\).
Find the \(x\)-intercept by substituting \(y=0\).	\(x=2(y-2)^{2}+1\) \(x=2(0-2)^{2}+1\) \(x=9\)
	The \(x\)-intercept is \((9,0)\).
Find the point symmetric to \((9,0)\) across the axis of symmetry.	\((9,4)\)
Find the \(y\)-intercepts. Let \(x=0\).
	A square cannot be negative, so there is no real solution. So there are no \(y\)-intercepts.
Graph the parabola.	$.$

	\(\stackrel{x=-4(y+1)^{2}+4}{x=a(y-k)^2+h}\)
Identify the constants \(a, h, k\).	\(a=-4, h=4, k=-1\)
Since \(a=-4\), the parabola opens to the left.
$.$
The axis of symmetry is \(y=k\).	The axis of symmetry is \(y=-1\).
The vertex is \((h,k)\).	The vertex is \((4,-1)\).
Find the \(x\)-intercept by substituting \(y=0\).	\(x=-4(y+1)^{2}+4\) \(x=-4(0+1)^{2}+4\) \(x=0\)
	The \(x\)-intercept is \((0,0)\).
Find the point symmetric to \((0,0)\) across the axis of symmetry.	\((0,-2)\)
Find the \(y\)-intercepts.	\(x=-4(y+1)^{2}+4\)
Let \(x=0\).
	\(y=-1+1 \quad y=-1-1\)
	\(y=0 \quad\quad y=-2\)
	The \(y\)-intercepts are \((0,0)\) and \((0,-2)\).
Graph the parabola.	$.$

Let the lower left side of the bridge be the origin of the coordinate grid at the point \((0,0)\). Since the base is \(20\) feet wide the point \((20,0)\) represents the lower right side. The bridge is 10 feet high at the highest point. The highest point is the vertex of the parabola so the \(y\)-coordinate of the vertex will be \(10\). Since the bridge is symmetric, the vertex must fall halfway between the left most point, \((0,0)\), and the rightmost point \((20,0)\). From this we know that the \(x\)-coordinate of the vertex will also be \(10\).	$.$
Identify the vertex, \((h,k)\).	\((h, k)=(10,10)\)
	\(h=10, \quad k=10\)
Substitute the values into the standard form. The value of \(a\) is still unknown. To find the value of \(a\) use one of the other points on the parabola.	\(\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}\)
Substitute the values of the other point into the equation.	\(y=a(x-10)^{2}+10\) \(0=a(0-10)^{2}+10\)
Solve for \(a\).
	\(y=a(x-10)^{2}+10\)
Substitute the value for \(a\) into the equation.	\(y=-\dfrac{1}{10}(x-10)^{2}+10\)