9.2: Evaluate Logarithms and Graph Basic Logarithmic Equations
- Page ID
- 66386
By the end of this section, you will be able to:
- Convert between exponential and logarithmic form
- Evaluate logarithmic expressions
- Graph basic logarithmic equations
- Solve logarithmic equations
- Use logarithmic models in applications
Before you get started, take this readiness quiz.
- Solve: \(x^{2}=81\).
- Evaluate: \(3^{−2}\).
- Solve: \(2^{4}=3x−5\).
We have spent some time solving many basic equations. It works well to ‘undo’ an operation with another operation. Subtracting ‘undoes’ addition, multiplication ‘undoes’ division, taking the square root ‘undoes’ squaring.
Because of the ono-to-one property of exponential expressions (for \(a\not=1\) and \(a>0\), if \(a^x=a^y\) then \(x=y\) ), the equation \(a^x=b\) has at most one solution. Also, it has a solution (as long as \(b>0\) since \(a^x>0\) for all \(x\)). To see why this is so consider this (non-linear) system of equations
\[\begin{cases}\begin{align} y=b\nonumber \\y=a^x\nonumber\end{align}.\end{cases}\]
The solution of this is also a solution to the equation \(a^x=b\) and graphically it is seen as the intersection of the two curves, and they can be seen to intersect as long as \(b>0\). Below is an example of such a situation.
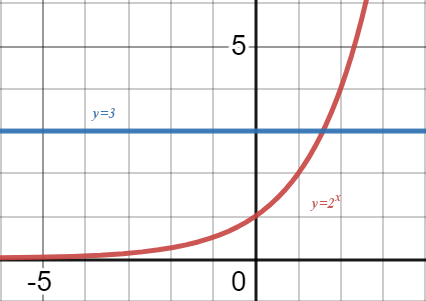
We can approximate the solution by trial and error with a calculator. But this is time consuming. Sometimes, as we have seen, we can solve these equations by hand, and fortunately, in other cases, our calculator can provide us with an approximation (after a little work, depending on the calculator).
We use the standard notation for the solution to \(a^x=b\). The solution is written \(x=\log_ab\).
The solution to the equation \(x=a^y\) is written
\(\log_{a}x\) and is called the logarithm of \(x\) with base \(a\), where \(a>0,x>0\), and \(a≠1\).
\(y=\log _{a} x\) is equivalent to \(x=a^{y}\)
Convert Between Exponential and Logarithmic Form
Since the equations \(y=\log _{a} x\) and \(x=a^{y}\) are equivalent, we can go back and forth between them. This will often be the method to solve some exponential and logarithmic equations. To help with converting back and forth let’s take a close look at the equations. See the figure below. Notice the positions of the exponent and base.
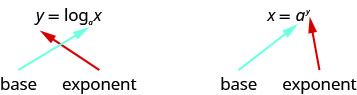
If we realize the logarithm is the exponent it makes the conversion easier. You may want to repeat, “base to the exponent give us the number.”
Convert to logarithmic form:
- \(2^{3}=8\)
- \(5^{\dfrac{1}{2}}=\sqrt{5}\)
- \(\left(\dfrac{1}{2}\right)^{x}=\dfrac{1}{16}\)
Solution:
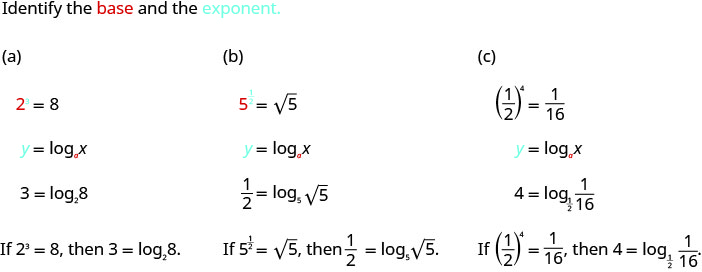
Convert to logarithmic form:
- \(3^{2}=9\)
- \(7^{\dfrac{1}{2}}=\sqrt{7}\)
- \(\left(\dfrac{1}{3}\right)^{x}=\dfrac{1}{27}\)
- Answer
-
- \(\log _{3} 9=2\)
- \(\log _{7} \sqrt{7}=\dfrac{1}{2}\)
- \(\log _{\dfrac{1}{3}} \dfrac{1}{27}=x\)
Convert to logarithmic form:
- \(4^{3}=64\)
- \(4^{\dfrac{1}{3}}=\sqrt[3]{4}\)
- \(\left(\dfrac{1}{2}\right)^{x}=\dfrac{1}{32}\)
- Answer
-
- \(\log _{4} 64=3\)
- \(\log _{4} \sqrt[3]{4}=\dfrac{1}{3}\)
- \(\log _{\dfrac{1}{2}} \dfrac{1}{32}=x\)
In the next example we do the reverse—convert logarithmic form to exponential form.
Convert to exponential form:
- \(2=\log _{8} 64\)
- \(0=\log _{4} 1\)
- \(-3=\log _{10} \dfrac{1}{1000}\)
Solution:
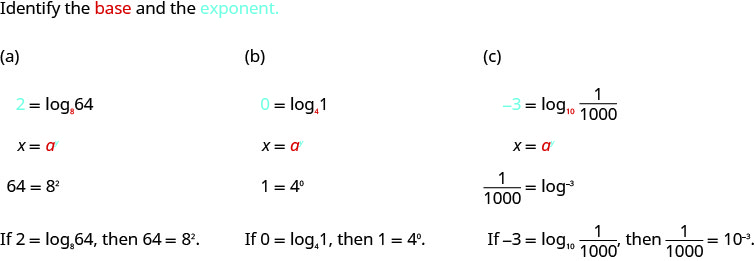
Convert to exponential form:
- \(3=\log _{4} 64\)
- \(0=\log _{x} 1\)
- \(-2=\log _{10} \dfrac{1}{100}\)
- Answer
-
- \(64=4^{3}\)
- \(1=x^{0}\)
- \(\dfrac{1}{100}=10^{-2}\)
Convert to exponential form:
- \(3=\log _{3} 27\)
- \(0=\log _{x} 1\)
- \(-1=\log _{10} \dfrac{1}{10}\)
- Answer
-
- \(27=3^{3}\)
- \(1=x^{0}\)
- \(\dfrac{1}{10}=10^{-1}\)
Evaluate Logarithmic Expressions
We can solve and evaluate logarithmic equations by using the technique of converting the equation to its equivalent exponential equation.
Find the value of \(x\):
a. \(\log _{x} 36=2\)
b. \(\log _{4} x=3\)
c. \(\log _{\dfrac{1}{2}} \dfrac{1}{8}=x\)
Solution:
a.
\(\log _{x} 36=2\)
Convert to exponential form.
\(x^{2}=36\)
Solve the quadratic.
\(x=6, \quad \cancel{x=-6}\)
The base of a logarithm must be positive, so we eliminate \(x=−6\).
\(x=6 \quad\) Therefore, \(\log _{6} 36=2\)
b.
\(\log _{4} x=3\)
Convert to exponential form.
\(4^{3}=x\)
Simplify.
\(x=64 \quad\) Therefore \(, \log _{4} 64=3\)
c.
\(\log _{\dfrac{1}{2}} \dfrac{1}{8}=x\)
Convert to exponential form.
\(\left(\dfrac{1}{2}\right)^{x}=\dfrac{1}{8}\)
Rewrite \(\dfrac{1}{8}\) as \(\left(\dfrac{1}{2}\right)^{3}\).
\(\left(\dfrac{1}{2}\right)^{x}=\left(\dfrac{1}{2}\right)^{3}\)
With the same base, the exponents must be equal.
\(x=3 \quad\) Therefore \(\log _{\dfrac{1}{2}} \dfrac{1}{8}=3\)
Find the value of \(x\):
a. \(\log _{x} 64=2\)
b. \(\log _{5} x=3\)
c. \(\log _{\dfrac{1}{2}} \dfrac{1}{4}=x\)
- Answer
-
a. \(x=8\)
b. \(x=125\)
c. \(x=2\)
Find the value of \(x\):
a. \(\log _{x} 81=2\)
b. \(\log _{3} x=5\)
c. \(\log _{\dfrac{1}{3}} \dfrac{1}{27}=x\)
- Answer
-
a. \(x=9\)
b. \(x=243\)
c. \(x=3\)
When see an expression such as \(\log_{3}27\), we can find its exact value two ways. By inspection we realize it means “\(3\) to what power will be \(27\)”? Since \(3^{3}=27\), we know \(\log_{3}27=3\). An alternate way is to set the expression equal to \(x\) and then convert it into an exponential equation.
Find the exact value of each logarithm without using a calculator:
a. \(\log _{5} 25\)
b. \(\log _{9} 3\)
c. \(\log _{2} \dfrac{1}{16}\)
Solution:
a.
\(\log _{5} 25\)
\(5\) to what power will be \(25\)?
\(\log _{5} 25=2\)
Or
Set the expression equal to \(x\).
\(\log _{5} 25=x\)
Change to exponential form.
\(5^{x}=25\)
Rewrite \(25\) as \(5^{2}\).
\(5^{x}=5^{2}\)
With the same base the exponents must be equal.
\(x=2 \quad\) Therefore \(, \log _{5} 25=2\).
b.
\(\log _{9} 3\)
Set the expression equal to \(x\).
\(\log _{9} 3=x\)
Change to exponential form.
\(9^{x}=3\)
Rewrite \(9\) as \(3^{2}\).
\(\left(3^{2}\right)^{x}=3^{1}\)
Simplify the exponents.
\(3^{2 x}=3^{1}\)
With the same base the exponents must be equal.
\(2 x=1\)
Solve the equation.
\(x=\dfrac{1}{2} \quad\) Therefore \(, \log _{9} 3=\dfrac{1}{2}\).
c.
\(\log _{2} \dfrac{1}{16}\)
Set the expression equal to \(x\).
\(\log _{2} \dfrac{1}{16}=x\)
Change to exponential form.
\(2^{x}=\dfrac{1}{16}\)
Rewrite \(16\) as \(2^{4}\).
\(2^{x}=\dfrac{1}{2^{4}}\)
\(2^{x}=2^{-4}\)
With the same base the exponents must be equal.
So, \(x=-4\) and therefore \(\log _{2} \dfrac{1}{16}=-4\)
Find the exact value of each logarithm without using a calculator:
a. \(\log _{12} 144\)
b. \(\log _{4} 2\)
c. \(\log _{2} \dfrac{1}{32}\)
- Answer
-
a. \(2\)
b. \(\dfrac{1}{2}\)
c. \(-5\)
Find the exact value of each logarithm without using a calculator:
a. \(\log _{9} 81\)
b. \(\log _{8} 2\)
c. \(\log _{3} \dfrac{1}{9}\)
- Answer
-
a. \(2\)
b. \(\dfrac{1}{3}\)
c. \(-2\)
Optional: Graph Basic Logarithmic Equations
To graph a logarithmic equation \(y=log_{a}x\), it is easiest to convert the equation to its exponential form, \(x=a^{y}\). Generally, when we look for ordered pairs for the graph of an equation, we usually choose an \(x\)-value and then determine its corresponding \(y\)-value. In this case you may find it easier to choose \(y\)-values and then determine its corresponding \(x\)-value.
Graph \(y=\log _{2} x\).
Solution:
To graph the equation, we will first rewrite the logarithmic equation, \(y=\log _{2} x\), in exponential form, \(2^{y}=x\). We can see that we have already graphed this (found the solutions to this equation, or rather the equation \(2^x=y\) from which we get the solutions by exchanging the order of the \(x-\)coordinate and the \(y-\)coordinate of each solution.)
Alternatively, we can use point plotting to graph the equation. It will be easier to start with values of \(y\) and then get \(x\).
| \(y\) | \(2^{y}=x\) | \((x,y)\) |
|---|---|---|
| \(-2\) | \(2^{-2}=\dfrac{1}{2^{2}}=\dfrac{1}{4}\) | \((\dfrac{1}{4},2)\) |
| \(-1\) | \(2^{-1}=\dfrac{1}{2^{1}}=\dfrac{1}{2}\) | \((\dfrac{1}{2},-1)\) |
| \(0\) | \(2^{0}=1\) | \((1,0)\) |
| \(1\) | \(2^{1}=2\) | \((2,1)\) |
| \(2\) | \(2^{2}=4\) | \((4,2)\) |
| \(3\) | \(2^{3}=8\) | \((8,3)\) |
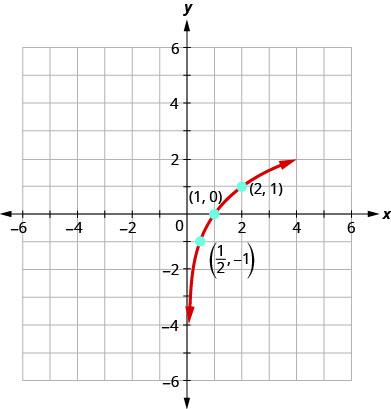
Graph: \(y=\log _{3} x\).
- Answer
-
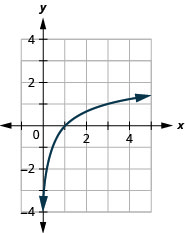
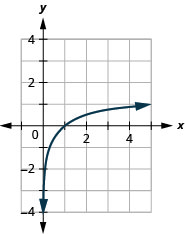
Graph: \(y=\log _{5} x\).
- Answer
-
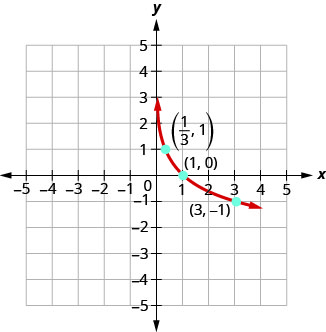
Graph \(y=\log _{\dfrac{1}{3}} x\).
Solution:
To graph the equation, we will first rewrite the logarithmic equation, \(y=\log _{\dfrac{1}{3}} x\), in exponential form, \(\left(\dfrac{1}{3}\right)^{y}=x\).
We will use point plotting to graph the equation. It will be easier to start with values of \(y\) and then get \(x\).
| \(y\) | \(\left(\dfrac{1}{3}\right)^{y}=x\) | \((x,y)\) |
|---|---|---|
| \(-2\) | \(\left(\dfrac{1}{3}\right)^{-2}=3^{2}=9\) | \((9,-2)\) |
| \(-1\) | \(\left(\dfrac{1}{3}\right)^{-1}=3^{1}=3\) | \((3,-1)\) |
| \(0\) | \(\left(\dfrac{1}{3}\right)^{0}=1\) | \((1,0)\) |
| \(1\) | \(\left(\dfrac{1}{3}\right)^{1}=\dfrac{1}{3}\) | \(\left(\dfrac{1}{3}, 1\right)\) |
| \(2\) | \(\left(\dfrac{1}{3}\right)^{2}=\dfrac{1}{9}\) | \(\left(\dfrac{1}{9}, 2\right)\) |
| \(3\) | \(\left(\dfrac{1}{3}\right)^{3}=\dfrac{1}{27}\) | \(\left(\dfrac{1}{27}, 3\right)\) |
Graph: \(y=\log _{\dfrac{1}{2}} x\).
- Answer
-
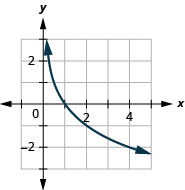
Graph: \(y=\log _{\dfrac{1}{4}} x\).
- Answer
-
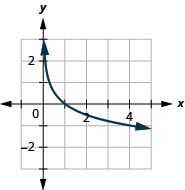
Solve Logarithmic Equations
When we talked about exponential expressions, we introduced the number \(e\). Just as \(e\) was a base for an exponential expression, it can be used as a base for logarithms too. The logarithm with base \(e\) is called the natural logarithm. The expression \(\log _{e} x\) is generally written \(\ln x\) and we read it as “el en of \(x\).”
\(\log_e x=\ln x\) is the natural logarithm where \(x>0\).
\(y=\ln x\) is equivalent to \(x=e^{y}\)
When the base of the logarithm is \(10\), we call it the common logarithmic and the base is not shown. If the base \(a\) of a logarithm is not shown, we assume it is \(10\). Note that in some texts it is assumed to be \(e\) in this case.
\(\log_{10}x=\log x\) is the common logarithm where \(x>0\).
\(y=\log x\) is equivalent to \(x=10^{y}\)

To solve logarithmic equations, one strategy is to change the equation to exponential form and then solve the exponential equation as we did before. As we solve basic logarithmic equations, \(y=log_{a}x\), we need to remember that for the base \(a\), \(a>0\) and \(a≠1\). Also, \(x>0\) since \(a^y>0\). Just as with radical equations, we must check our solutions to eliminate any extraneous solutions.
Solve:
a. \(\log _{a} 49=2\)
b. \(\ln x=3\)
Solution:
a. \(\log _{a} 49=2\)
Rewrite in exponential form.
\(a^{2}=49\)
Solve the equation using the square root property.
\(a=\pm 7\)
The base cannot be negative, so we eliminate \(a=-7\).
\(a=7, \quad \cancel{a=-7}\)
Check. \(a=7\)
\(\begin{aligned} \log _{a} 49&=2 \\ \log_{7}49&\stackrel{?}{=}2 \\ 7^{2}&\stackrel{?}{=}49 \\ 49& \stackrel{?}{=} 49\text{ True} \end{aligned}\)
b.
\(\ln x=3\)
Rewrite in exponential form.
\(e^{3}=x\)
Check. \(x=e^{3}\)
\(\begin{aligned} \ln x &=3 \\ \ln e^{3} & \stackrel{?}{=} 3 \\ e^{3}&\stackrel{?}{=}e^{3}\text{ True} \end{aligned}\)
Solve:
a. \(\log _{a} 121=2\)
b. \(\ln x=7\)
- Answer
-
a. \(a=11\)
b. \(x=e^{7}\)
Solve:
a. \(\log _{a} 64=3\)
b. \(\ln x=9\)
- Answer
-
a. \(a=4\)
b. \(x=e^{9}\)
Solve:
a. \(\log _{2}(3 x-5)=4\)
b. \(\ln e^{2 x}=4\)
Solution:
a.
\(\log _{2}(3 x-5)=4\)
Rewrite in exponential form.
\(2^{4}=3 x-5\)
Simplify.
\(16=3 x-5\)
Solve the equation.
\(21=3 x\)
\(7=x\)
Check. \(x=7\)
\(\begin{aligned} \log _{2}(3 x-5)&=4 \\ \log_{2}(3\cdot7-5)&\stackrel{?}{=}4\\ \log_{2}(16)&\stackrel{?}{=}4 \\ 2^{4}& \stackrel{?}{=}16 \\ 16&=16 \end{aligned}\)
b.
\(\ln e^{2 x}=4\)
Rewrite in exponential form.
\(e^{4}=e^{2 x}\)
Since the bases are the same the exponents are equal.
\(4=2 x\)
Solve the equation.
\(2=x\)
Check. \(x=2\)
\(\begin{aligned} \ln e^{2 x} &=4 \\ \ln e^{2 \cdot 2} & \stackrel{?}{=} 4 \\ \ln e^{4} &\stackrel{?}{=}4 \\ e^{4} &\stackrel{?}{=}e^{4}\text{ True} \end{aligned}\)
Solve:
a. \(\log _{2}(5 x-1)=6\)
b. \(\ln e^{3 x}=6\)
- Answer
-
a. \(x=13\)
b. \(x=2\)
Solve:
a. \(\log _{3}(4 x+3)=3\)
b. \(\ln e^{4 x}=4\)
- Answer
-
a. \(x=6\)
b. \(x=1\)
Use Logarithmic Models in Applications
There are many applications that are modeled by logarithmic equations. We will first look at the logarithmic equation that gives the decibel (dB) level of sound. Decibels range from \(0\), which is barely audible to \(160\), which can rupture an eardrum. The \(10^{−12}\) in the formula represents the intensity of sound that is barely audible.
Decibel Level of Sound
The loudness level, \(D\), measured in decibels, of a sound of intensity, \(I\), measured in watts per square inch is
\(D=10 \log \left(\dfrac{I}{10^{-12}}\right)\)
Extended exposure to noise that measures \(85\) dB can cause permanent damage to the inner ear which will result in hearing loss. What is the decibel level of music coming through ear phones with intensity \(10^{−2}\) watts per square inch?
Solution:
|
\(D=10\log\left(\dfrac{I}{10^{-12}}\right)\) |
|
| Substitute in the intensity level, \(I\). |
\(D=10\log\left(\dfrac{10^{-2}}{10^{-12}}\right)\) |
| Simplify. |
\(D=10\log(10^{10})\) |
| Since \(\log 10^{10}=10\). |
\(D=10\cdot 10\) |
| Multiply. |
\(D=100\) |
| The decibel level of music coming through earphones is \(100\) dB. |
What is the decibel level of one of the new quiet dishwashers with intensity \(10^{−7}\) watts per square inch?
- Answer
-
The quiet dishwashers have a decibel level of \(50\) dB.
What is the decibel level heavy city traffic with intensity \(10^{−3}\) watts per square inch?
- Answer
-
The decibel level of heavy traffic is \(90\) dB.
The magnitude \(R\) of an earthquake is measured by a logarithmic scale called the Richter scale. The model is \(R=\log I\), where \(I\) is the intensity of the shock wave. This model provides a way to measure earthquake intensity.
The magnitude \(R\) of an earthquake is measured by\(R=\log I\), where \(I\) is the intensity of its shock wave.
In 1906, San Francisco experienced an intense earthquake with a magnitude of \(7.8\) on the Richter scale. Over \(80\)% of the city was destroyed by the resulting fires. In 2014, Los Angeles experienced a moderate earthquake that measured \(5.1\) on the Richter scale and caused $\(108\) million dollars of damage. Compare the intensities of the two earthquakes.
Solution:
To compare the intensities, we first need to convert the magnitudes to intensities using the log formula. Then we will set up a ratio to compare the intensities.
Convert the magnitudes to intensities.
\(R=\log I\)
1906 earthquake
\(7.8=\log I\)
Convert to exponential form.
\(I=10^{7.8}\)
2014 earthquake
\(5.1=\log I\)
Convert to exponential form.
\(I=10^{5.1}\)
Form a ratio of the intensities.
\(\dfrac{\text { Intensity for } 1906}{\text { Intensity for } 2014}\)
Substitute in the values.
\(\dfrac{10^{7.8}}{10^{5.1}}\)
Divide by subtracting the exponents.
\(10^{2.7}\)
Evaluate.
\(501\)
The intensity of the 1906 earthquake was about \(501\) times the intensity of the 2014 earthquake.
In 1906, San Francisco experienced an intense earthquake with a magnitude of \(7.8\) on the Richter scale. In 1989, the Loma Prieta earthquake also affected the San Francisco area, and measured \(6.9\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
The intensity of the 1906 earthquake was about \(8\) times the intensity of the 1989 earthquake.
In 2014, Chile experienced an intense earthquake with a magnitude of \(8.2\) on the Richter scale. In 2014, Los Angeles also experienced an earthquake which measured \(5.1\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
The intensity of the earthquake in Chile was about \(1,259\) times the intensity of the earthquake in Los Angeles.
Key Concepts
- Evaluation of logarithms
- (Optional) Basic shape of the graph of \(y=\log _{a} x\) for various \(a\) values.
- Decibel Level of Sound: The loudness level, \(D\), measured in decibels, of a sound of intensity, \(I\), measured in watts per square inch is \(D=10 \log \left(\dfrac{I}{10^{-12}}\right)\).
- Earthquake Intensity: The magnitude \(R\) of an earthquake is measured by \(R=\log I\), where \(I\) is the intensity of its shock wave.
Glossary
- common logarithm
- \(\log_{10}x=\log x\) is the common logarithm, where \(x>0\).
\(y=\log x\) is equivalent to \(x=10^{y}\)
- logarithm
- For \(a>0, a\not=1\) and \(x>0\), the solution to the equation \(a^y=x\) is denoted \(\log _{a} x\) is called the logarithm of \(x\) with base \(a\). \(y=\log _{a} x\) is equivalent to \(x=a^{y}\)
- natural logarithm
- \(\log_{e}x=\ln x\) is the natural logarithm, where \(x>0\).
\(y=\ln x\) is equivalent to \(x=e^{y}\)
Practice Makes Perfect
Note that even answers are provided in this section.
In the following exercises, convert from exponential to logarithmic form.
- \(4^{2}=16\)
- \(2^{5}=32\)
- \(3^{3}=27\)
- \(5^{3}=125\)
- \(10^{3}=1000\)
- \(10^{-2}=\dfrac{1}{100}\)
- \(x^{\frac{1}{2}}=\sqrt{3}\)
- \(x^{\frac{1}{3}}=\sqrt[3]{6}\)
- \(32^{x}=\sqrt[4]{32}\)
- \(17^{x}=\sqrt[5]{17}\)
- \(\left(\dfrac{1}{4}\right)^{2}=\dfrac{1}{16}\)
- \(\left(\dfrac{1}{3}\right)^{4}=\dfrac{1}{81}\)
- \(3^{-2}=\dfrac{1}{9}\)
- \(4^{-3}=\dfrac{1}{64}\)
- \(e^{x}=6\)
- \(e^{3}=x\)
- Answer
-
2. \(\log _{2} 32=5\)
4. \(\log _{5} 125=3\)
6. \(\log \dfrac{1}{100}=-2\)
8. \(\log _{x} \sqrt[3]{6}=\dfrac{1}{3}\)
10. \(\log _{17} \sqrt[5]{17}=x\)
12. \(\log _{\dfrac{1}{3}} \dfrac{1}{81}=4\)
14. \(\log _{4} \dfrac{1}{64}=-3\)
16. \(\ln x=3\)
In the following exercises, convert each logarithmic equation to exponential form.
- \(3=\log _{4} 64\)
- \(6=\log _{2} 64\)
- \(4=\log _{x} 81\)
- \(5=\log _{x} 32\)
- \(0=\log _{12} 1\)
- \(0=\log _{7} 1\)
- \(1=\log _{3} 3\)
- \(1=\log _{9} 9\)
- \(-4=\log _{10} \dfrac{1}{10,000}\)
- \(3=\log _{10} 1,000\)
- \(5=\log _{e} x\)
- \(x=\log _{e} 43\)
- Answer
-
18. \(64=2^{6}\)
20. \(32=x^{5}\)
22. \(1=7^{0}\)
24. \(9=9^{1}\)
26. \(1,000=10^{3}\)
28. \(43=e^{x}\)
In the following exercises, find the value of \(x\) in each logarithmic equation.
- \(\log _{x} 49=2\)
- \(\log _{x} 121=2\)
- \(\log _{x} 27=3\)
- \(\log _{x} 64=3\)
- \(\log _{3} x=4\)
- \(\log _{5} x=3\)
- \(\log _{2} x=-6\)
- \(\log _{3} x=-5\)
- \(\log _{\frac{1}{4}} \dfrac{1}{16}=x\)
- \(\log _{\frac{1}{3}} \dfrac{1}{9}=x\)
- \(\log _{\frac{1}{4}} 64=x\)
- \(\log _{\frac{1}{9}} 81=x\)
- Answer
-
30. \(x=11\)
32. \(x=4\)
34. \(x=125\)
36. \(x=\dfrac{1}{243}\)
38. \(x=2\)
40. \(x=-2\)
In the following exercises, find the exact value of each logarithm without using a calculator.
- \(\log _{7} 49\)
- \(\log _{6} 36\)
- \(\log _{4} 1\)
- \(\log _{5} 1\)
- \(\log _{16} 4\)
- \(\log _{27} 3\)
- \(\log _{\frac{1}{2}} 2\)
- \(\log _{\frac{1}{2}} 4\)
- \(\log _{2} \dfrac{1}{16}\)
- \(\log _{3} \dfrac{1}{27}\)
- \(\log _{4} \dfrac{1}{16}\)
- \(\log _{9} \dfrac{1}{81}\)
- Answer
-
42. \(2\)
44. \(0\)
46. \(\dfrac{1}{3}\)
48. \(-2\)
50. \(-3\)
52. \(-2\)
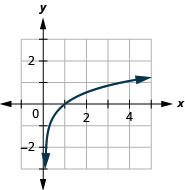
In the following exercises, graph each logarithmic function.
- \(y=\log _{2} x\)
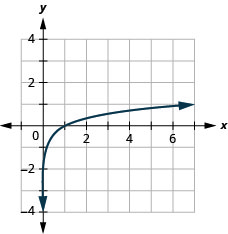
- \(y=\log _{4} x\)
- \(y=\log _{6} x\)
- \(y=\log _{7} x\)
- \(y=\log _{1.5} x\)
- \(y=\log _{2.5} x\)
- \(y=\log _{\frac{1}{3}} x\)
- \(y=\log _{\frac{1}{5}} x\)
- \(y=\log _{0.4} x\)
- \(y=\log _{0.6} x\)
- Answer
-
54.
56.
58.
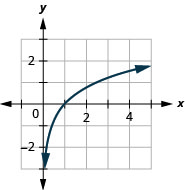
60.
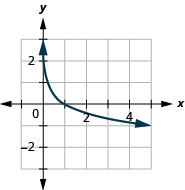
62.
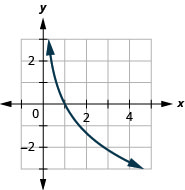
In the following exercises, solve each logarithmic equation.
- \(\log _{a} 16=2\)
- \(\log _{a} 81=2\)
- \(\log _{a} 8=3\)
- \(\log _{a} 27=3\)
- \(\log _{a} 32=2\)
- \(\log _{a} 24=3\)
- \(\ln x=5\)
- \(\ln x=4\)
- \(\log _{2}(5 x+1)=4\)
- \(\log _{2}(6 x+2)=5\)
- \(\log _{3}(4 x-3)=2\)
- \(\log _{3}(5 x-4)=4\)
- \(\log _{4}(5 x+6)=3\)
- \(\log _{4}(3 x-2)=2\)
- \(\ln e^{4 x}=8\)
- \(\ln e^{2 x}=6\)
- \(\log x^{2}=2\)
- \(\log \left(x^{2}-25\right)=2\)
- \(\log _{2}\left(x^{2}-4\right)=5\)
- \(\log _{3}\left(x^{2}+2\right)=3\)
- Answer
-
64. \(a=9\)
66. \(a=3\)
68. \(a=\sqrt[3]{24}\)
70. \(x=e^{4}\)
72. \(x=5\)
74. \(x=17\)
76. \(x=6\)
78. \(x=3\)
80. \(x=-5 \sqrt{5}, x=5 \sqrt{5}\)
82. \(x=-5, x=5\)
In the following exercises, use a logarithmic model to solve.
- What is the decibel level of normal conversation with intensity \(10^{−6}\) watts per square inch?
- What is the decibel level of a whisper with intensity \(10^{−10}\) watts per square inch?
- What is the decibel level of the noise from a motorcycle with intensity \(10^{−2}\) watts per square inch?
- What is the decibel level of the sound of a garbage disposal with intensity \(10^{−2}\) watts per square inch?
- In 2014, Chile experienced an intense earthquake with a magnitude of \(8.2\) on the Richter scale. In 2010, Haiti also experienced an intense earthquake which measured \(7.0\) on the Richter scale. Compare the intensities of the two earthquakes.
- The Los Angeles area experiences many earthquakes. In 1994, the Northridge earthquake measured magnitude of \(6.7\) on the Richter scale. In 2014, Los Angeles also experienced an earthquake which measured \(5.1\) on the Richter scale. Compare the intensities of the two earthquakes.
- Answer
-
84. A whisper has a decibel level of \(20\) dB.
86. The sound of a garbage disposal has a decibel level of \(100\) dB.
88. The intensity of the 1994 Northridge earthquake in the Los Angeles area was about \(40\) times the intensity of the 2014 earthquake.
- Explain how to change an equation from logarithmic form to exponential form.
- Explain the difference between common logarithms and natural logarithms.
- Explain why \(\log _{a} a^{x}=x\).
- Explain how to find the \(\log _{7} 32\) on your calculator.
- Answer
-
90. Answers may vary
92. Answers may vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
| I can... | Confidently | With some help | No- I don't get it! |
|---|---|---|---|
| Convert between exponential and logarithmic form. | |||
| Evaluate logarithms. | |||
| Graph basic logarithmic equations. | |||
| Solve logarithm equations. | |||
| Use logarithmic models in applications. |
b. After reviewing this checklist, what will you do to become confident for all objectives?


