3.2: Visualizing Groups- Cayley Graphs
- Page ID
- 692
So far, we've seen three different kinds of groups: Groups of symmetries (including the dihedral group of symmetries of a polygon), the integers modulo \(n\), and the permutation group, \(S_n\). We've seen Cayley graphs for the dihedral group; let's see some Cayley graphs for some others.
Integers Modulo \(n\)
The integers modulo \(n\) only require a single generator to obtain the entire group. \(1\) is a nice choice of generator, as we know that every number \(k\) in \(\{0,1,2,\ldots n\}\) can be written as \(k\cdot 1\), which is to say, the sum of \(1\) with itself \(k\) times. The Cayley graph for this situation is simple: it's just \(n\) vertices, arranged in a loop with an arrow pointing from each number to the next. This creates a cycle! When \(n=8\), the cycle is this: \[0\rightarrow 1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 5\rightarrow 6\rightarrow 7\rightarrow 0\]. Any group which is generated by a single element (including the usual integers!) is called a cyclic group. (This is yet another interpretation of \(\mathbb{Z}_n\)!)
We can choose other numbers than \(1\) as the generator, though! Take \(n=8\), and consider the number \(3\). We can make our Cayley graph by drawing a vertex for each number in \(\{0,1,2,\ldots,8\}\) and an arrow from each \(x\) to \(x+3\). Then the cycle draws out as: [0\rightarrow 3\rightarrow 6\rightarrow 1\rightarrow 4\rightarrow 7\rightarrow 2\rightarrow 5\rightarrow 0].
Here's a Cayley graph for \(\mathbb{Z}_7\) shown with three generators. Any one of the three generators would work just fine. The red vertex is the identity, \(0\). The green arrows are for the generator \(1\), blue for the generator \(2\), and green for the generator \(3\). What would happen if we included the generators \(4, 5,\) or \(6\)?
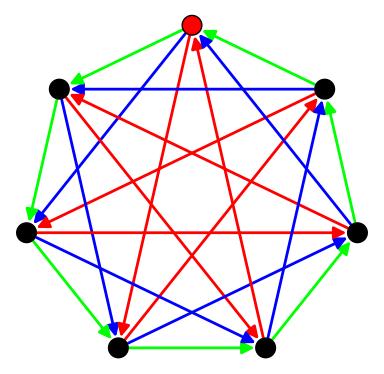
Figure 3.1: Cayley graph for \(\mathbb{Z}_7\) with three different generators. The identity is marked as the red dot.
Not every number is a generator of \(\mathbb{Z}_n\). For example, in \(\mathbb{Z}_8\), if we choose \(4\), the cycle is just: \( 0\rightarrow 4\rightarrow 0\). Since the cycle doesn't contain every element of the group, we see that \(4\) doesn't generate the group on its own.
Suppose \(k\in \mathbb{Z}_n\). Show that \(k\) generates \(\mathbb{Z}_n\) if and only if \(k\) is relatively prime to \(n\). (ie, the only common divisor of \(k\) and \(n\) is \(1\).)
Suppose \(k\in \mathbb{Z}_n\) and \(k\) is not relatively prime to \(n\). Is it possible to find another umber \(m\) not relatively prime to \(n\) such that \(k\) and \(m\) together generate \(\mathbb{Z}_n\)? Try some examples! Explain why or why not
Permutation Groups
The permutation group \(S_n\) has a number of interesting generating sets. We'll show a few of these generating sets for \(n=3\) and \(n=4\) for easy comparison.
The first generating set is a minimal set, using just two generators. The first generator is the 'rotation' with list notation \(r=[n,1,2,3,4,\ldots, n-1]\). The second is a flip, exchanging only the first two things, \(f=[2,1,3,4,\ldots,n]\).
To check that these actually generate \(S_n\), we need to see that we can construct an arbitrary permutation using just these generators. So consider an arbitrary permutation \(\sigma\), written in list notation. If there are two adjacent entries that are out of order (big to the left of the small), we can apply rotations until the two things sit in the first two entries (suppose we use \(k\) rotations to do this). Then we apply the flip. And then we 'unrotate' \(k\) times to put the now-sorted numbers back. Then we find two more adjacent numbers and repeat. Once there are no adjacent numbers out of order, then we must be at the identity! Then the reverse of the sequence of moves we just made builds the permutation we wanted. Since the permutation was arbitrary, our two moves must generate the group.
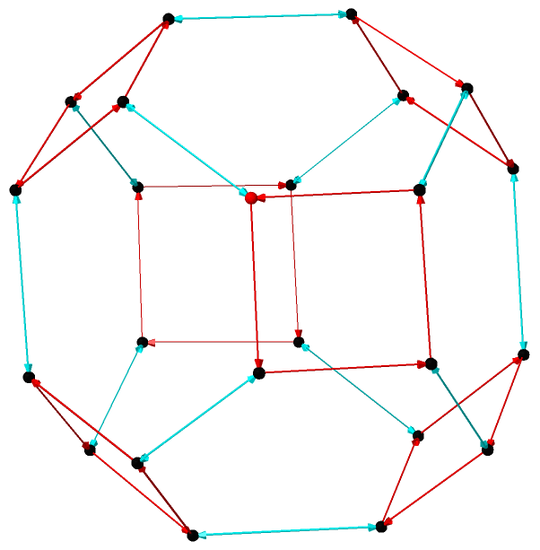
Figure 3.2: A Cayley graph for \(S_4\), generated by the rotation \([4,1,2,3]\) (in red) and reflection \([2,1,3,4]) (cyan).
A second set of generators is given by the set of all transpositions. These are all of the permutations that have two things switched and everything else in order. For example, \([4,2,3,1]\) and \([1,2,6,4,5,3]\) are transpositions. Modifying the above argument, you can see that the set of all transpositions are a generating set. There are more than 2 transpositions, so this isn't a minimal generating set. But it is an interesting set of generators when studying the permutation group more closely.
| Exercise 3.1.2 |
|---|
| How many transpositions are there in \(S_n\)? |
Yet a third set of generators is given by the simple transpositions. This is the set of transpositions \(\{s_i\}\) that just exchange \(i\) and \(i+1\) while leaving everything else alone. There are \(n-1\) simple transpositions. This is a very important set of generators in the further study of permutations! But it shows up in one simple context, as well.
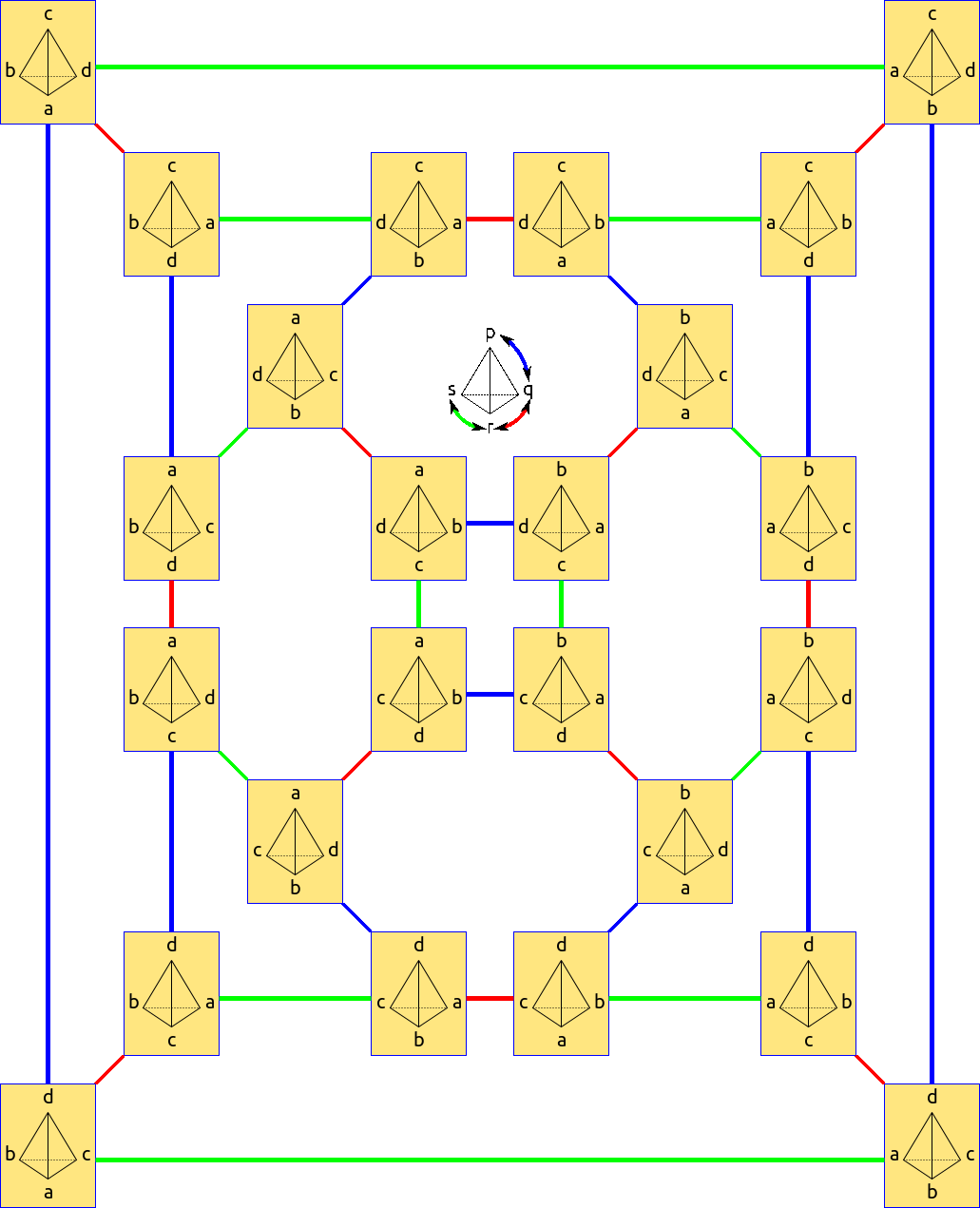
Figure 3.1.3: Cayley graph for \(S_4\); permutations are marked by different symmetries of the tetrahedron. Generators are three 'flips' exchanging two vertices.
A basic problem in computer science is sorting. Given a list of \(n\) things, how quickly can they be sorted? What is a good algorithm for sorting an arbitrary list? There are many different sorting algorithms. One of the easiest is called Bubble Sort. For bubble sort, you read through the list, beginning to end, and whenever you see two adjacent entries that are out of order, you switch them. You may have to read through the list performing switches many times, but eventually the list will be sorted. Bubble Sort uses the fact that the simple transpositions are a generating set for the permutations in order to sort an arbitrary list. (This is the first step into the study of complexity theory.)
What permutation of \(n\) things takes the longest to be sorted by Bubble Sort? How many simple transpositions are necessary to sort that permutation?
For the same 'long' permutation from the last exercise, sort the permutation using the first set of generators for \(S_n\), the rotation and the flip. How many steps are needed to sort the permutation this way?
We see that there's a trade-off between having a smaller set of generators and being able to write different group elements as products of fewer generators. (Indeed, if we took the whole group as the generating set, every element could be written as a product of just one generator! But this usually isn't so helpful for understanding the group...)
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


